沪科版数学九年级上册 22.1 相似形课件(共22张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 22.1 相似形课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 543.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 21:12:04 | ||
图片预览




文档简介
(共22张PPT)
相似形
相似图形的概念:
在数学上,我们把具有形状相同的图形称为相似图形。
注意:相似图形的大小不一定相同。
A
A
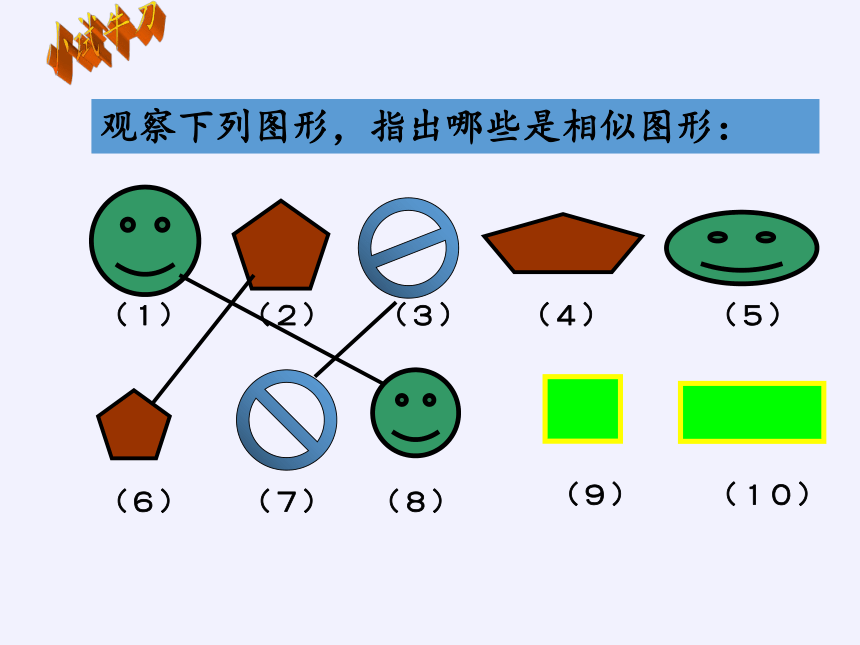
观察下列图形,指出哪些是相似图形:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
小试牛刀
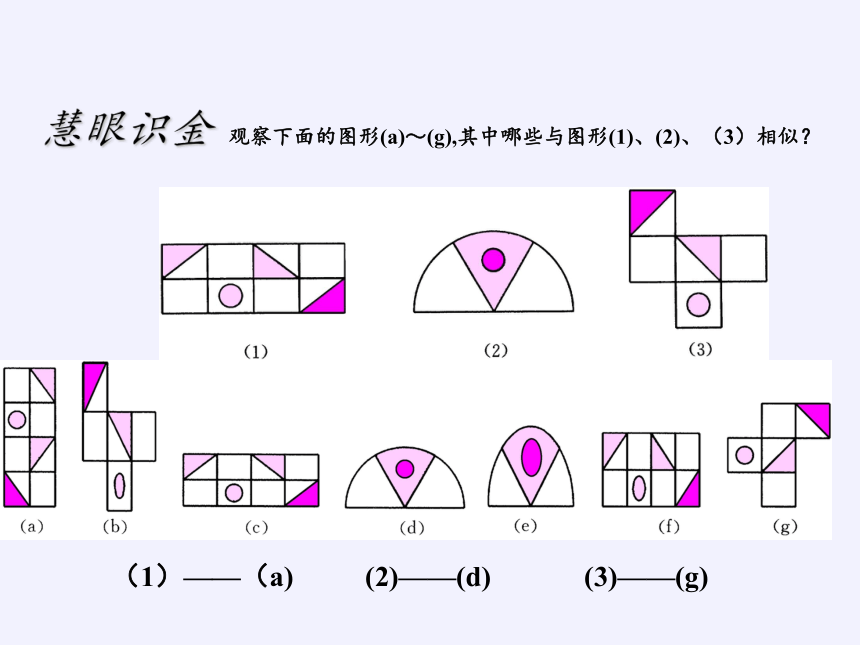
慧眼识金
观察下面的图形(a)~(g),其中哪些与图形(1)、(2)、(3)相似?
(1)——(a) (2)——(d) (3)——(g)
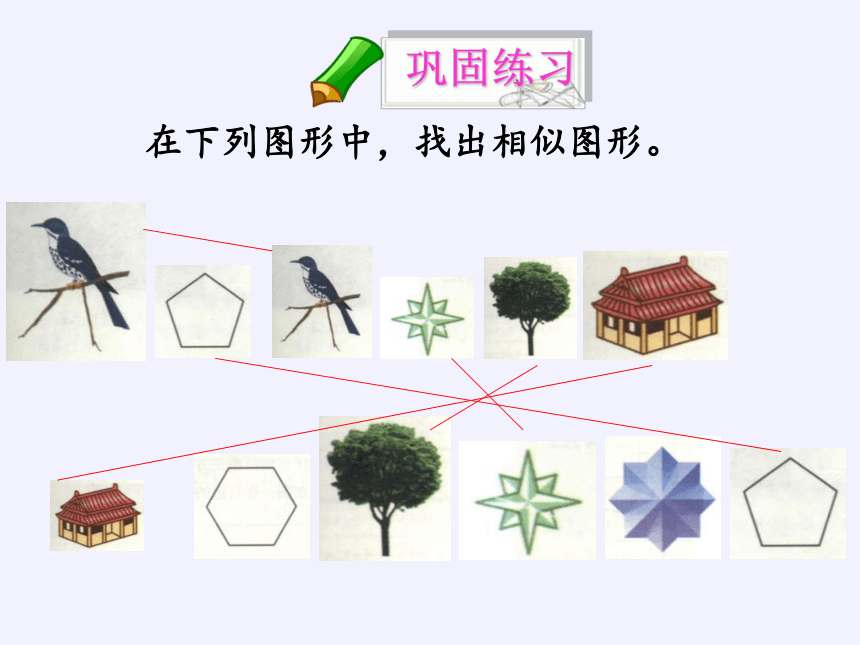
在下列图形中,找出相似图形。
巩固练习
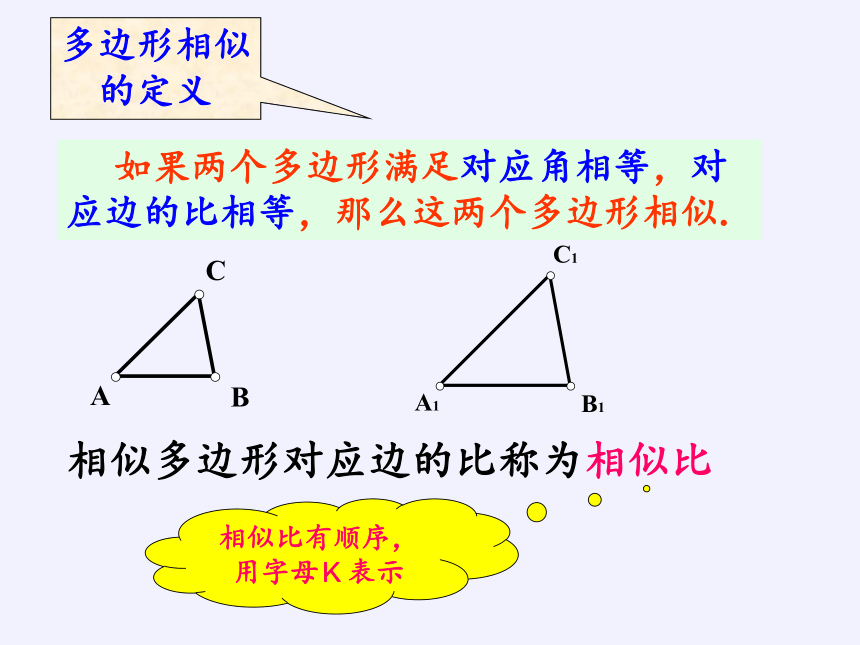
如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似.
C1
B1
A1
多边形相似的定义
相似多边形对应边的比称为相似比
相似比有顺序,用字母K表示
C
B
A
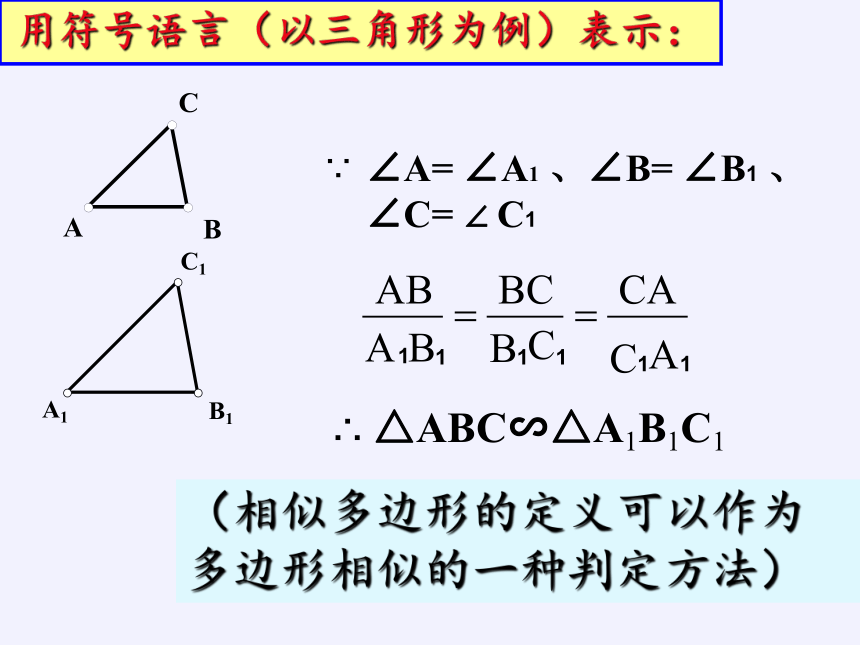
用符号语言(以三角形为例)表示:
∵
∠A= ∠A1 、∠B= ∠B1 、∠C= ∠ C1
∴ △ABC∽△A1B1C1
(相似多边形的定义可以作为多边形相似的一种判定方法)
1
A
1
C
CA
1
C
1
B
BC
1
B
1
A
AB
=
=
C1
B1
A1
例1:如图所示的两个三角形一定相似吗?为什么?
10
5
5
10
相 似
A
B
C
D
E
F
G
H
解: ∵ 矩形的每个内角都等于90o.
∴ ∠A =∠E = 90°,∠B =∠F = 90°
∠C =∠G = 90°,∠D =∠H = 90°
∴ 它们的对应角相等.
∵ EH:AD=300:(300+2×7.5)=20/21.
EF:AB =150:(150+2×7.5)=10/11.
∴ EH:AD≠EF:AB.
∴ 它们的对应边不成比例.
∴ 矩形ABCD和矩形EFGH不相似.
一块长 3m,宽1.5m的矩形黑板,镶其外围的木质边宽7.5cm。边框内外边缘所组成的矩形相似吗 为什么
例:2:
相似的正多边形的特征:
对应角相等,对应边的比相等.
相似多边形的特征:
对应角相等,对应边的比相等.
符号语言(以四边形为例):
∵四边形ABCD∽四边形A1B1C1D1
D
D
C
C
B
B
A
A
1
=
1
=
1
=
1
=
,
,
,
A
D
DA
D
C
CD
C
B
BC
B
A
AB
1
1
=
1
1
=
1
1
=
1
1
\
例 3:如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
试一试:如图所示的两个五边形相似,求 未知边a、b、c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
∴ = = = =
解:∵两个五边形相似
∴ a = 3 , b = 4.5 , c = 4 , d = 6
5
.
7
5
a
2
b
3
6
c
9
d
随堂练习
1. 判断:
(1)任意两个矩形都是相似图形( )
(2)任意两个圆形是相似图形( )
(3)对应角相等的两个四边形是相似多边形( )
(4)两个正五边形是相似多边形( )
(5)两个全等三角形是相似多边形( )
(6)两菱形是相似多边形( )
(7)两个相似多边形,对应边成比例( )
√
√
√
×
√
×
×
2. 五边形ABCDE相似于五边形A′B′C′D′E′,它们的相似比为1 : 3,(1)若∠D=135°,则∠D′= ______。
(2)若A′B′=15cm,则AB= ______。
135°
5
3. 一个多边形的边长分别是2、3、4、5、6,另一个和它相似的多边形的最短边长为6,则这个多边形的最长边为______ 。
18
课后作业: 求相似多边形的对应角或对应边
五边形ABCDE相似于五边形FGHIJ,且AB=2cm,CD=3cm,DE=2.2cm,GH=6cm,HI =5cm,FJ=4cm, ∠A=120°,∠H=90°
求:(1)相似比等于多少
(2)FG,IJ,BC,AE, ∠F, ∠C
A
B
C
D
E
F
G
H
I
J
5
解:(1)相似比=CD : HI=3 : 5
(2)∵五边形ABCDE相似于五边形FGHIJ
∴ ∠F =∠A=120o, ∠C= ∠H=90o,
∴AB : FG = BC : GH = CD : HI = DE : IJ = EA : JF
即2 : FG = BC : 6 = 3/5 = 2.2 : IJ = AE :4
解得FG =10/3 cm, BC =18/5cm,IJ=11/3cm,AE=12/5cm
A
B
C
D
E
F
G
H
I
J
2
3
2.2
6
5
4
120°
课堂小结:
1.谈谈本节课你有什么收获
2.通过本节课的学习你还有什么疑惑?
课后作业
1、课后练习
2、优化设计同步练习
谢 谢
相似形
相似图形的概念:
在数学上,我们把具有形状相同的图形称为相似图形。
注意:相似图形的大小不一定相同。
A
A
观察下列图形,指出哪些是相似图形:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
小试牛刀
慧眼识金
观察下面的图形(a)~(g),其中哪些与图形(1)、(2)、(3)相似?
(1)——(a) (2)——(d) (3)——(g)
在下列图形中,找出相似图形。
巩固练习
如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似.
C1
B1
A1
多边形相似的定义
相似多边形对应边的比称为相似比
相似比有顺序,用字母K表示
C
B
A
用符号语言(以三角形为例)表示:
∵
∠A= ∠A1 、∠B= ∠B1 、∠C= ∠ C1
∴ △ABC∽△A1B1C1
(相似多边形的定义可以作为多边形相似的一种判定方法)
1
A
1
C
CA
1
C
1
B
BC
1
B
1
A
AB
=
=
C1
B1
A1
例1:如图所示的两个三角形一定相似吗?为什么?
10
5
5
10
相 似
A
B
C
D
E
F
G
H
解: ∵ 矩形的每个内角都等于90o.
∴ ∠A =∠E = 90°,∠B =∠F = 90°
∠C =∠G = 90°,∠D =∠H = 90°
∴ 它们的对应角相等.
∵ EH:AD=300:(300+2×7.5)=20/21.
EF:AB =150:(150+2×7.5)=10/11.
∴ EH:AD≠EF:AB.
∴ 它们的对应边不成比例.
∴ 矩形ABCD和矩形EFGH不相似.
一块长 3m,宽1.5m的矩形黑板,镶其外围的木质边宽7.5cm。边框内外边缘所组成的矩形相似吗 为什么
例:2:
相似的正多边形的特征:
对应角相等,对应边的比相等.
相似多边形的特征:
对应角相等,对应边的比相等.
符号语言(以四边形为例):
∵四边形ABCD∽四边形A1B1C1D1
D
D
C
C
B
B
A
A
1
=
1
=
1
=
1
=
,
,
,
A
D
DA
D
C
CD
C
B
BC
B
A
AB
1
1
=
1
1
=
1
1
=
1
1
\
例 3:如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
试一试:如图所示的两个五边形相似,求 未知边a、b、c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
∴ = = = =
解:∵两个五边形相似
∴ a = 3 , b = 4.5 , c = 4 , d = 6
5
.
7
5
a
2
b
3
6
c
9
d
随堂练习
1. 判断:
(1)任意两个矩形都是相似图形( )
(2)任意两个圆形是相似图形( )
(3)对应角相等的两个四边形是相似多边形( )
(4)两个正五边形是相似多边形( )
(5)两个全等三角形是相似多边形( )
(6)两菱形是相似多边形( )
(7)两个相似多边形,对应边成比例( )
√
√
√
×
√
×
×
2. 五边形ABCDE相似于五边形A′B′C′D′E′,它们的相似比为1 : 3,(1)若∠D=135°,则∠D′= ______。
(2)若A′B′=15cm,则AB= ______。
135°
5
3. 一个多边形的边长分别是2、3、4、5、6,另一个和它相似的多边形的最短边长为6,则这个多边形的最长边为______ 。
18
课后作业: 求相似多边形的对应角或对应边
五边形ABCDE相似于五边形FGHIJ,且AB=2cm,CD=3cm,DE=2.2cm,GH=6cm,HI =5cm,FJ=4cm, ∠A=120°,∠H=90°
求:(1)相似比等于多少
(2)FG,IJ,BC,AE, ∠F, ∠C
A
B
C
D
E
F
G
H
I
J
5
解:(1)相似比=CD : HI=3 : 5
(2)∵五边形ABCDE相似于五边形FGHIJ
∴ ∠F =∠A=120o, ∠C= ∠H=90o,
∴AB : FG = BC : GH = CD : HI = DE : IJ = EA : JF
即2 : FG = BC : 6 = 3/5 = 2.2 : IJ = AE :4
解得FG =10/3 cm, BC =18/5cm,IJ=11/3cm,AE=12/5cm
A
B
C
D
E
F
G
H
I
J
2
3
2.2
6
5
4
120°
课堂小结:
1.谈谈本节课你有什么收获
2.通过本节课的学习你还有什么疑惑?
课后作业
1、课后练习
2、优化设计同步练习
谢 谢
