24.1.4圆周角定理
图片预览



文档简介
课件37张PPT。23.1 圆周角 复习旧知:我们是如何给圆心角下定义的?顶点在圆心的角叫圆心角。 考考你:你能仿照圆心角的定义,
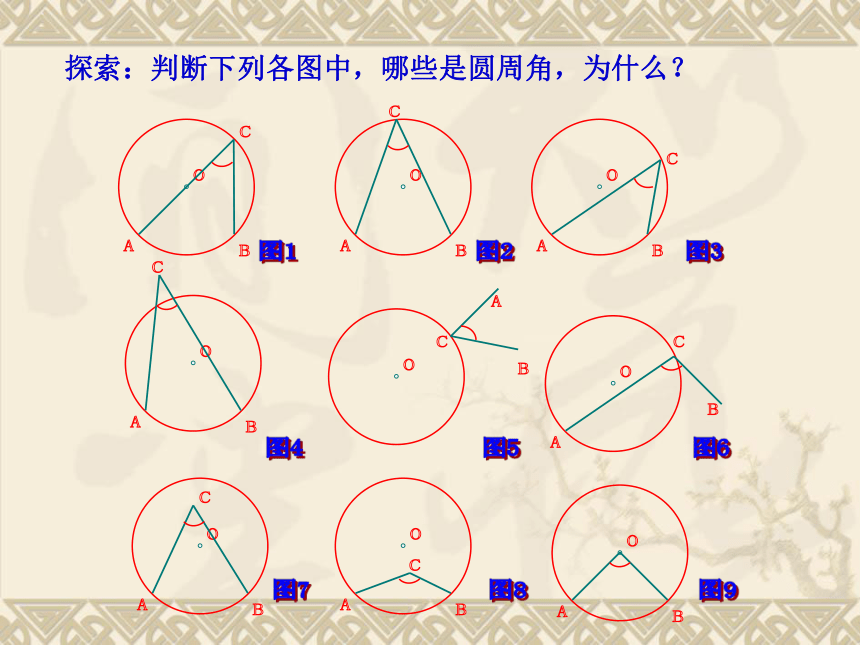
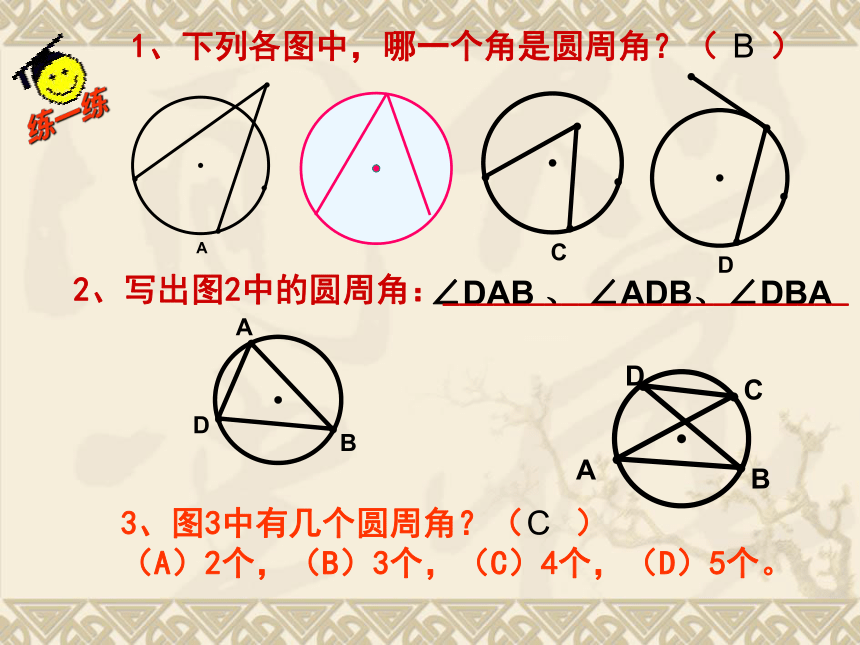
给∠ACB 这样的角下个定义吗?顶点在圆上,并且两边都和圆相交的角叫做圆周角. 探索:判断下列各图中,哪些是圆周角,为什么? oABoABoABoABoABoABoABoABCCCCCCCC图1图2图3图4图5图6图7图8图9∠DAB 、 ∠ADB、∠DBA 练一练1、下列各图中,哪一个角是圆周角?( )
3、图3中有几个圆周角?( )
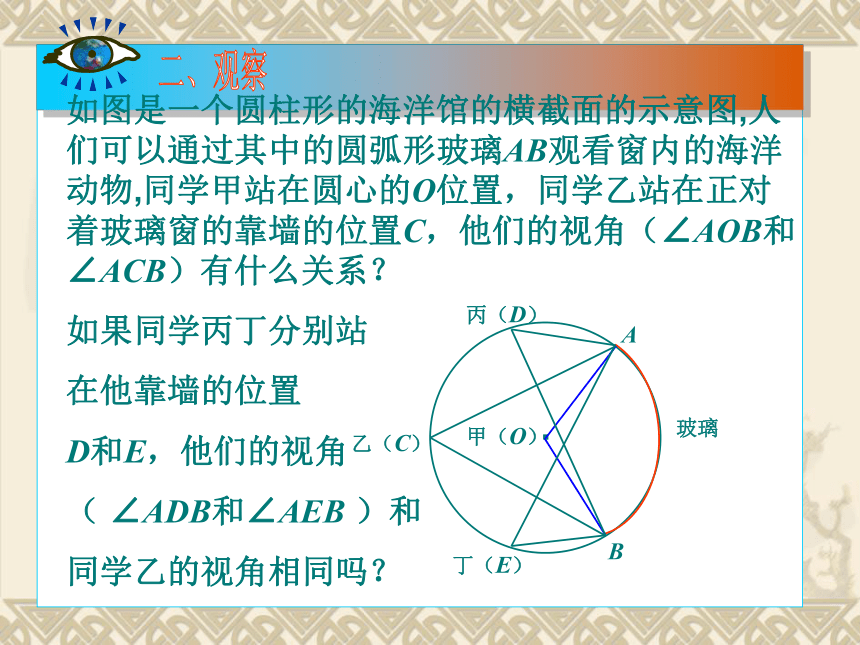
(A)2个,(B)3个,(C)4个,(D)5个。BC2、写出图2中的圆周角:________________________如图是一个圆柱形的海洋馆的横截面的示意图,人们可以通过其中的圆弧形玻璃AB观看窗内的海洋动物,同学甲站在圆心的O位置,同学乙站在正对着玻璃窗的靠墙的位置C,他们的视角(∠AOB和∠ACB)有什么关系?
如果同学丙丁分别站
在他靠墙的位置
D和E,他们的视角
( ∠ADB和∠AEB )和
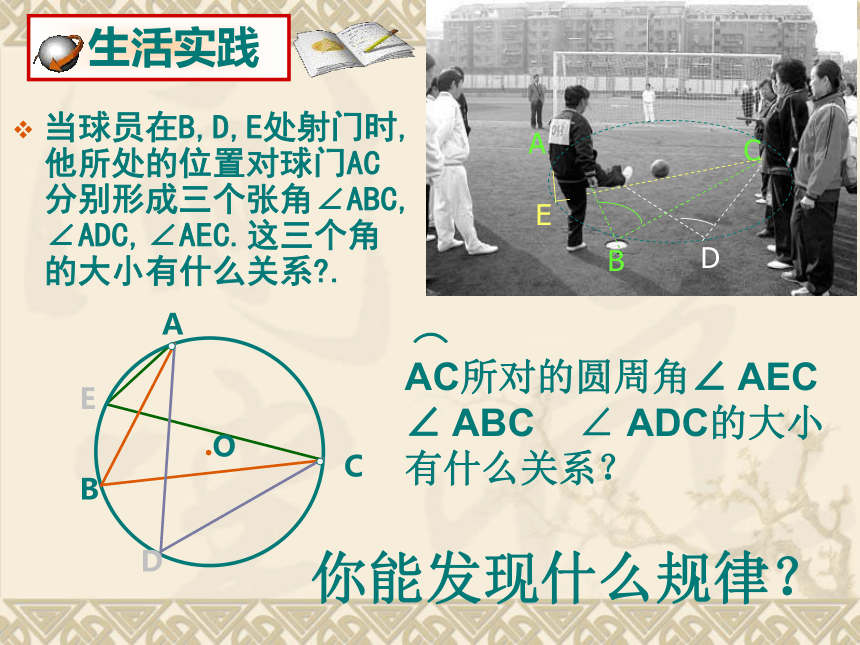
同学乙的视角相同吗?·二、观察AB甲(O)乙(C)丙(D)丁(E)玻璃当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.你能发现什么规律?在同一个圆中一条弧所对的圆周角有多少个?
2.这些圆周角的度数是否发生变化?(用量角器量量看)
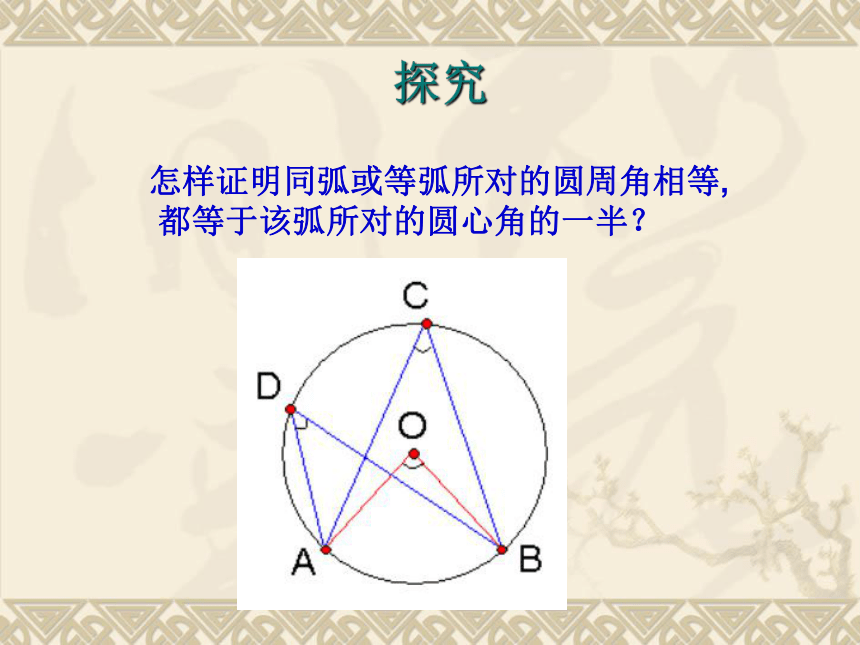
3.同一条弧所对的圆周角与圆心角有什么关系?(用量角器量量看)(画图观察)思考以下问题:探索2:(有无数个)(同一条弧所对的圆周角相等)探究怎样证明同弧或等弧所对的圆周角相等,
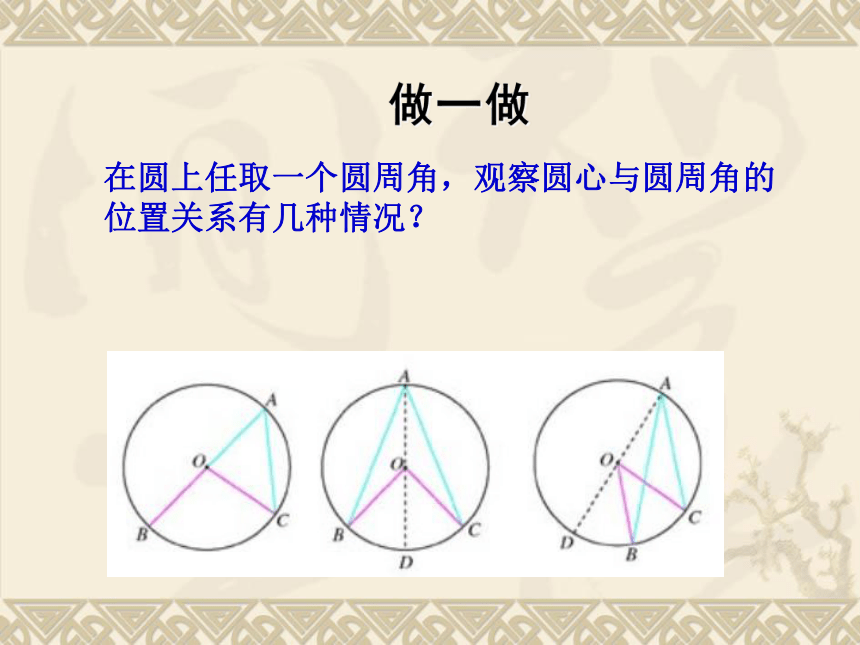
都等于该弧所对的圆心角的一半? 做一做 在圆上任取一个圆周角,观察圆心与圆周角的
位置关系有几种情况?
分三种情况来证明:
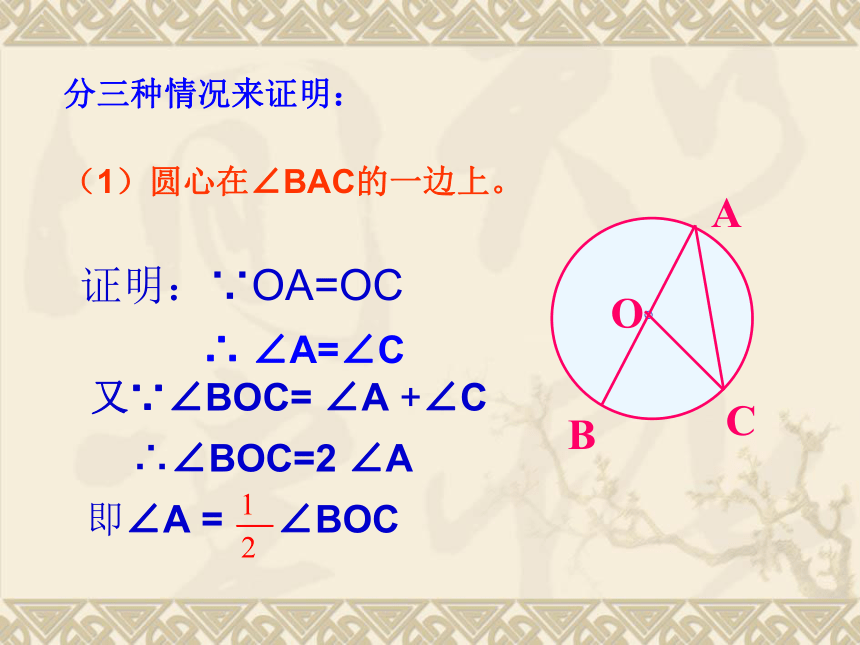
(1)圆心在∠BAC的一边上。
∴ ∠A=∠C证明:∵OA=OC 又∵∠BOC= ∠A +∠C
∴∠BOC=2 ∠A
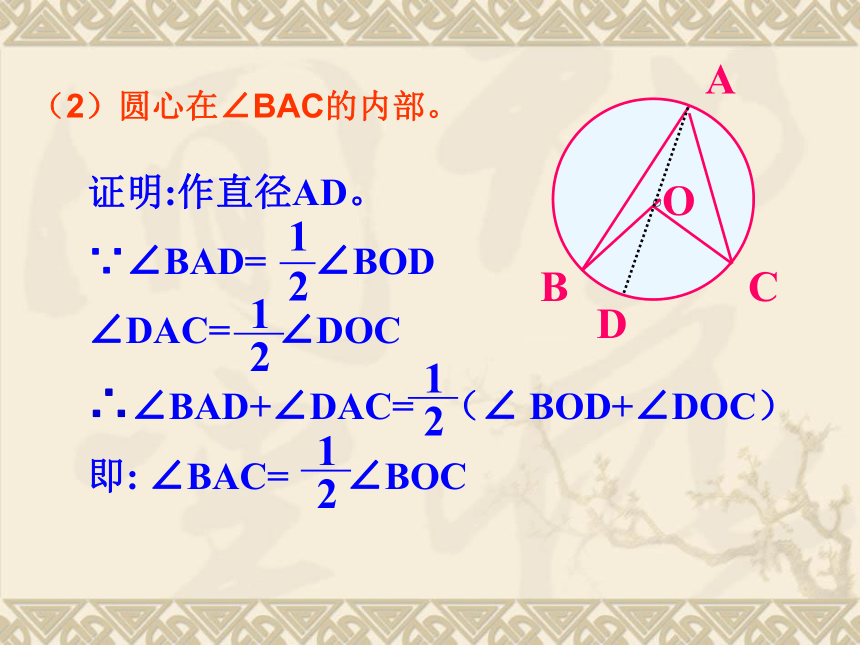
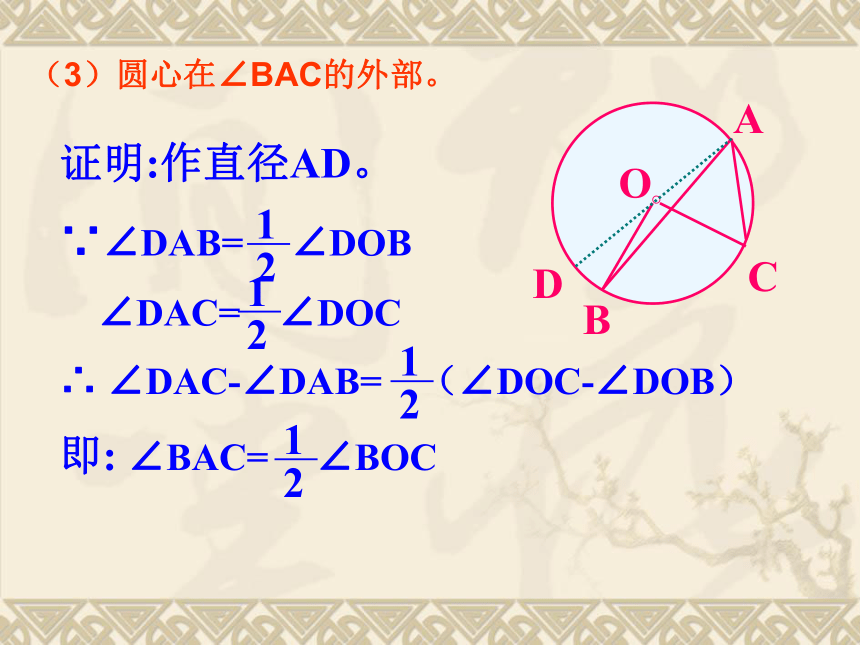
即∠A = ∠BOC(2)圆心在∠BAC的内部。(3)圆心在∠BAC的外部。D 综上所述,我们可以得到:圆周角定理: 在同圆 中,同弧 所对的圆周角 都等于这条弧所对的圆心角的一半。 或等圆或等弧相等,思考:
相等的圆周角所对的弧相等吗?
答:一定相等。在同圆或等圆中,练习:2.试找出下图中所有相等的圆周角。 ∠2=∠7∠1=∠4∠3=∠6∠5=∠8练一练3、如图,在⊙O中,∠ABC=50°,
则∠AOC等于( )
A、50°; B、80°;
C、90°; D、100°D4、如图,△ABC是等边三角形,
动点P在圆周的劣弧AB上,且不
与A、B重合,则∠BPC等于( )
A、30°; B、60°;
C、90°; D、45°B练一练5、如图,∠A=50°, ∠AOC=60 °
BD是⊙O的直径,则∠AEB等于( )
A、70°; B、110°;
C、90°; D、120°B6、如图,△ABC的顶点A、B、C
在⊙O上,∠C=30 °,AB=2,
则⊙O的半径是 。解:连接OA、OB∵∠C=30 ° ,∴∠AOB=60 °又∵OA=OB ,∴△AOB是等边三角形∴OA=OB=AB=2,半径是2。23.如图,∠A是圆O的圆周角,
∠A=40°,求∠OBC的度数。 4.已知,四边形ABCD的顶点在⊙O上, ∠BCD=120°,则∠BOD 。探索3如图,线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B),那么,∠ACB就是直径AB所对的圆周角,想想看,∠ACB会是怎样的角?思考
90°的圆周角所对的弦是什么? 从而得出结论:
90°的圆周角所对的弦是直径半圆(或直径)所对的圆周角是直角例题1、 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD有什么关系.为什么?变:若AC交⊙O于点E,
求证:CD=DE=BD 例题2、如图,已知A、B、C、D、E 均在⊙O上,且AC为⊙O的直径,求
∠A+ ∠B+ ∠C的值。圆内接多边形与多边形的外接圆:
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形;
这个圆叫做这个多边形的外接圆.例如:如图,四边形ABCD是⊙O的 ;
⊙O是四边形ABCD的 .探究:圆内接四边形ABCD的对角∠B与∠D有什么关系?6、证明:已知:如图,四边形ABCD的四个顶点在⊙O上,求证:∠B+∠D=1800结论:圆的内接四边形对角互补。如图,A、B、C、D是⊙O上的四个点,且∠BCD=100°,求∠BOD( 所对的圆心角)
和∠BAD的大小。变形题:已知ABC三点在圆O上,依次连接ABCO,若∠AOC=140度,求∠B的度数。110度已知圆心角可构造同弧所对的圆周角.DOCBAD例 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.又在Rt△ABD中,AD2+BD2=AB2,解:∵AB是直径,∴ ∠ACB= ∠ADB=90°.在Rt△ABC中,∵CD平分∠ACB,∴AD=BD.七、例题2.如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下.DOOO·方法一方法二方法三方法四AB使用帮助求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)·ABCO求证: △ABC 为直角三角形.证明:CO= AB,以AB为直径作⊙O,∵AO=BO, ∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴∠ACB= ×180°= 90°.∴ △ABC 为直角三角形.练 习综合练习一:
一、判断正误:
1.同弧或等弧所对的圆周角相等( )
2.相等的圆周角所对的弧相等( )
3.90°角所对的弦是直径( )
4.直径所对的角等于90°( )
5.长等于半径的弦所对的圆周角等于30°( )1、100o的弧所对的圆心角等于_______,所对的圆周角等于_______。
2、一弦分圆周角成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为________________。
3、如图,在⊙O中,∠BAC=32o,则∠BOC=________。
4、如图,⊙O中,∠ACB = 130o,则∠AOB=______。
5、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角。
(B)60o的圆周角所对的弧的度数是30o
(C)一弧所对的圆周角等于它所对的圆心角。
(D)120o的弧所对的圆周角是60oB
100o50o36o或144o64o100oD综合练习二6、如图,在⊙O中,∠BOC =50°,则∠A的度数为 。.7、已知:△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=60°,则∠AOB的度数为 。
8、已知⊙O中弦AB的等于半径,求 弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。25014009、如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.40°10、如图,BD为⊙O的直径,∠A=30°,BC=4,则BD=_______5008探究3、如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC交⊙O于点F,点F不与点A重合。
(1)AB与AC的大小有什么关系?为什么?
(2)按角的大小分类,请你判断△ABC属于哪一类三角形,并说明理由。∴△ABC是锐角三角形解:(1)AB=AC。证明:连接AD又∵DC=BD,∴AB=AC。(2)△ABC是锐角三角形。由(1)知,∠B=∠C<90 °连接BF,则∠AFB=90 °,∴∠A<90 °∵AB是直径,∴∠ADB=90°,实践应用:
船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁。弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区?(1)当船与两个灯塔的夹角∠α大于“危险角”时,船位于哪个区域?为什么?(2)当船与两个灯塔的夹角∠α小于“危险角”时,船位于哪个区域?为什么?小结:
1、圆周角定理:同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
2、圆周角定理的推论:直径所对的圆周角是直角,900的圆周角所对的弦是直径.
3、圆的内接四边形对角互补。
(在圆中,常作直径,构造直角三角形)
给∠ACB 这样的角下个定义吗?顶点在圆上,并且两边都和圆相交的角叫做圆周角. 探索:判断下列各图中,哪些是圆周角,为什么? oABoABoABoABoABoABoABoABCCCCCCCC图1图2图3图4图5图6图7图8图9∠DAB 、 ∠ADB、∠DBA 练一练1、下列各图中,哪一个角是圆周角?( )
3、图3中有几个圆周角?( )
(A)2个,(B)3个,(C)4个,(D)5个。BC2、写出图2中的圆周角:________________________如图是一个圆柱形的海洋馆的横截面的示意图,人们可以通过其中的圆弧形玻璃AB观看窗内的海洋动物,同学甲站在圆心的O位置,同学乙站在正对着玻璃窗的靠墙的位置C,他们的视角(∠AOB和∠ACB)有什么关系?
如果同学丙丁分别站
在他靠墙的位置
D和E,他们的视角
( ∠ADB和∠AEB )和
同学乙的视角相同吗?·二、观察AB甲(O)乙(C)丙(D)丁(E)玻璃当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.你能发现什么规律?在同一个圆中一条弧所对的圆周角有多少个?
2.这些圆周角的度数是否发生变化?(用量角器量量看)
3.同一条弧所对的圆周角与圆心角有什么关系?(用量角器量量看)(画图观察)思考以下问题:探索2:(有无数个)(同一条弧所对的圆周角相等)探究怎样证明同弧或等弧所对的圆周角相等,
都等于该弧所对的圆心角的一半? 做一做 在圆上任取一个圆周角,观察圆心与圆周角的
位置关系有几种情况?
分三种情况来证明:
(1)圆心在∠BAC的一边上。
∴ ∠A=∠C证明:∵OA=OC 又∵∠BOC= ∠A +∠C
∴∠BOC=2 ∠A
即∠A = ∠BOC(2)圆心在∠BAC的内部。(3)圆心在∠BAC的外部。D 综上所述,我们可以得到:圆周角定理: 在同圆 中,同弧 所对的圆周角 都等于这条弧所对的圆心角的一半。 或等圆或等弧相等,思考:
相等的圆周角所对的弧相等吗?
答:一定相等。在同圆或等圆中,练习:2.试找出下图中所有相等的圆周角。 ∠2=∠7∠1=∠4∠3=∠6∠5=∠8练一练3、如图,在⊙O中,∠ABC=50°,
则∠AOC等于( )
A、50°; B、80°;
C、90°; D、100°D4、如图,△ABC是等边三角形,
动点P在圆周的劣弧AB上,且不
与A、B重合,则∠BPC等于( )
A、30°; B、60°;
C、90°; D、45°B练一练5、如图,∠A=50°, ∠AOC=60 °
BD是⊙O的直径,则∠AEB等于( )
A、70°; B、110°;
C、90°; D、120°B6、如图,△ABC的顶点A、B、C
在⊙O上,∠C=30 °,AB=2,
则⊙O的半径是 。解:连接OA、OB∵∠C=30 ° ,∴∠AOB=60 °又∵OA=OB ,∴△AOB是等边三角形∴OA=OB=AB=2,半径是2。23.如图,∠A是圆O的圆周角,
∠A=40°,求∠OBC的度数。 4.已知,四边形ABCD的顶点在⊙O上, ∠BCD=120°,则∠BOD 。探索3如图,线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B),那么,∠ACB就是直径AB所对的圆周角,想想看,∠ACB会是怎样的角?思考
90°的圆周角所对的弦是什么? 从而得出结论:
90°的圆周角所对的弦是直径半圆(或直径)所对的圆周角是直角例题1、 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD有什么关系.为什么?变:若AC交⊙O于点E,
求证:CD=DE=BD 例题2、如图,已知A、B、C、D、E 均在⊙O上,且AC为⊙O的直径,求
∠A+ ∠B+ ∠C的值。圆内接多边形与多边形的外接圆:
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形;
这个圆叫做这个多边形的外接圆.例如:如图,四边形ABCD是⊙O的 ;
⊙O是四边形ABCD的 .探究:圆内接四边形ABCD的对角∠B与∠D有什么关系?6、证明:已知:如图,四边形ABCD的四个顶点在⊙O上,求证:∠B+∠D=1800结论:圆的内接四边形对角互补。如图,A、B、C、D是⊙O上的四个点,且∠BCD=100°,求∠BOD( 所对的圆心角)
和∠BAD的大小。变形题:已知ABC三点在圆O上,依次连接ABCO,若∠AOC=140度,求∠B的度数。110度已知圆心角可构造同弧所对的圆周角.DOCBAD例 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.又在Rt△ABD中,AD2+BD2=AB2,解:∵AB是直径,∴ ∠ACB= ∠ADB=90°.在Rt△ABC中,∵CD平分∠ACB,∴AD=BD.七、例题2.如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下.DOOO·方法一方法二方法三方法四AB使用帮助求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)·ABCO求证: △ABC 为直角三角形.证明:CO= AB,以AB为直径作⊙O,∵AO=BO, ∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴∠ACB= ×180°= 90°.∴ △ABC 为直角三角形.练 习综合练习一:
一、判断正误:
1.同弧或等弧所对的圆周角相等( )
2.相等的圆周角所对的弧相等( )
3.90°角所对的弦是直径( )
4.直径所对的角等于90°( )
5.长等于半径的弦所对的圆周角等于30°( )1、100o的弧所对的圆心角等于_______,所对的圆周角等于_______。
2、一弦分圆周角成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为________________。
3、如图,在⊙O中,∠BAC=32o,则∠BOC=________。
4、如图,⊙O中,∠ACB = 130o,则∠AOB=______。
5、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角。
(B)60o的圆周角所对的弧的度数是30o
(C)一弧所对的圆周角等于它所对的圆心角。
(D)120o的弧所对的圆周角是60oB
100o50o36o或144o64o100oD综合练习二6、如图,在⊙O中,∠BOC =50°,则∠A的度数为 。.7、已知:△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=60°,则∠AOB的度数为 。
8、已知⊙O中弦AB的等于半径,求 弦AB所对的圆心角和圆周角的度数。 圆心角为60度圆周角为 30 度或 150 度。25014009、如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.40°10、如图,BD为⊙O的直径,∠A=30°,BC=4,则BD=_______5008探究3、如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC交⊙O于点F,点F不与点A重合。
(1)AB与AC的大小有什么关系?为什么?
(2)按角的大小分类,请你判断△ABC属于哪一类三角形,并说明理由。∴△ABC是锐角三角形解:(1)AB=AC。证明:连接AD又∵DC=BD,∴AB=AC。(2)△ABC是锐角三角形。由(1)知,∠B=∠C<90 °连接BF,则∠AFB=90 °,∴∠A<90 °∵AB是直径,∴∠ADB=90°,实践应用:
船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁。弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区?(1)当船与两个灯塔的夹角∠α大于“危险角”时,船位于哪个区域?为什么?(2)当船与两个灯塔的夹角∠α小于“危险角”时,船位于哪个区域?为什么?小结:
1、圆周角定理:同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
2、圆周角定理的推论:直径所对的圆周角是直角,900的圆周角所对的弦是直径.
3、圆的内接四边形对角互补。
(在圆中,常作直径,构造直角三角形)
同课章节目录
