八年级上册第十二章 全等三角形之全等三角形垂直模型(教案)
文档属性
| 名称 | 八年级上册第十二章 全等三角形之全等三角形垂直模型(教案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 10:31:06 | ||
图片预览


文档简介
常见的三垂直模型:
三垂直模型
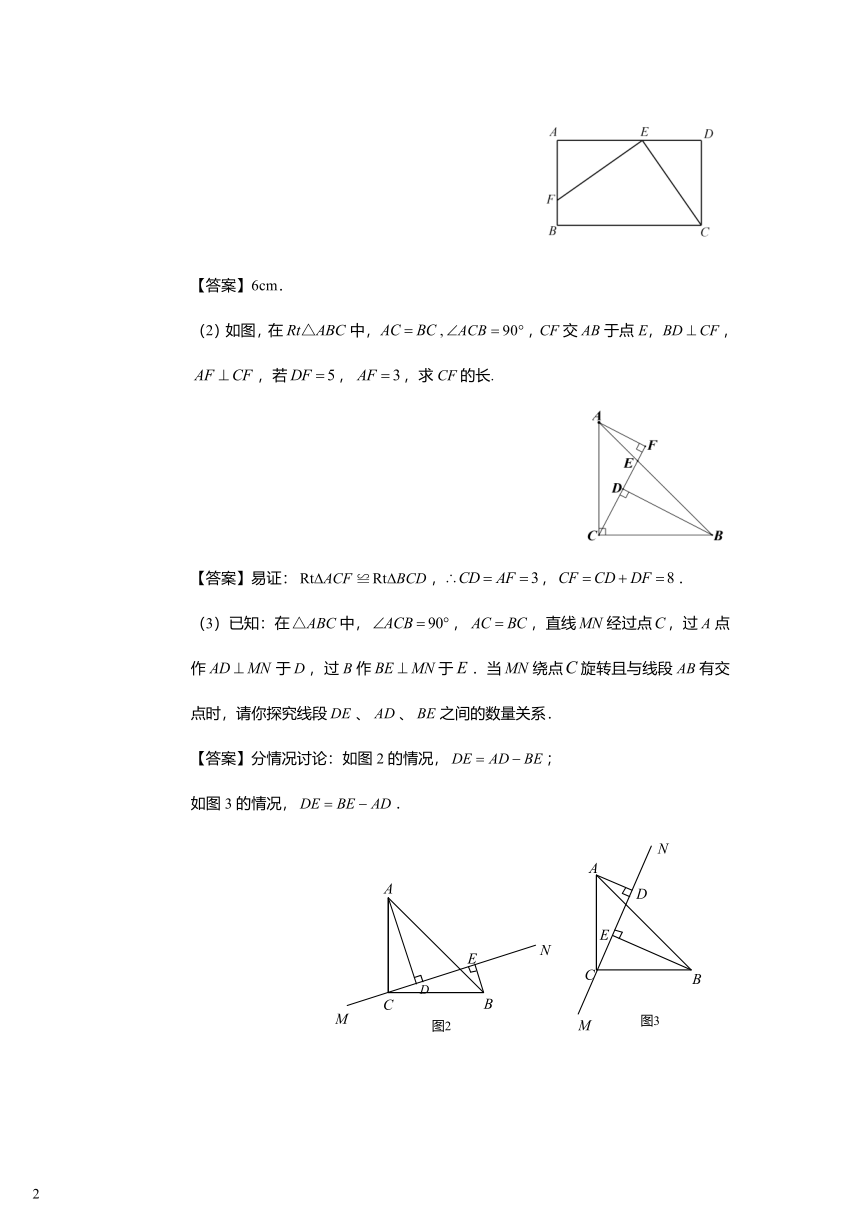
(1)如图,已知矩形中,E是AD上的一点,F是AB上的一点,,且,,矩形的周长为32cm,求AE的长.
【答案】6cm.
(2)如图,在中,,,CF交AB于点E,,,若,,求CF的长.
【答案】易证:,∴,.
(3)已知:在中,,,直线经过点,过A点作于,过B作于.当绕点旋转且与线段AB有交点时,请你探究线段、、之间的数量关系.
【答案】分情况讨论:如图2的情况,;
如图3的情况,.
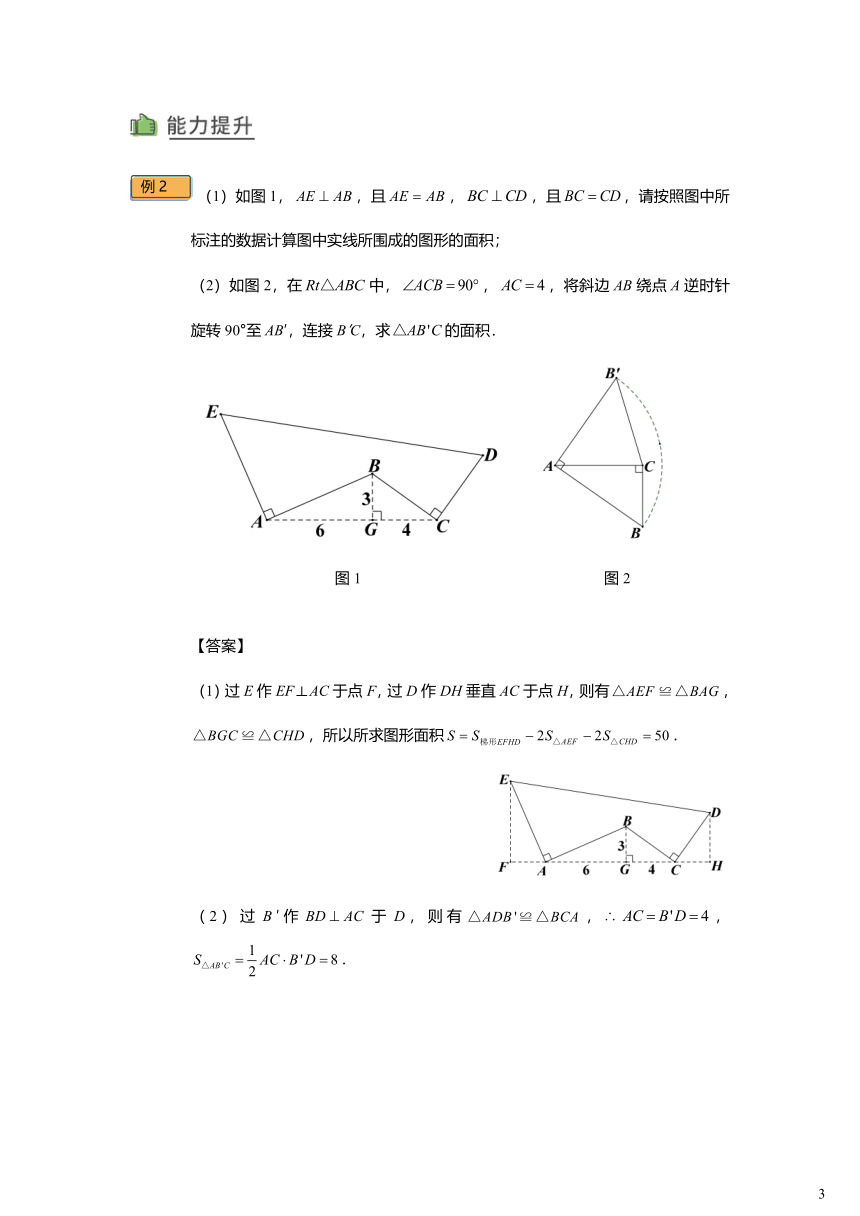
(1)如图1,,且,,且,请按照图中所标注的数据计算图中实线所围成的图形的面积;
(2)如图2,在中,,,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求的面积.
图1 图2
【答案】
(1)过E作EF⊥AC于点F,过D作DH垂直AC于点H,则有,,所以所求图形面积.
(2)过B′作于D,则有,∴,.
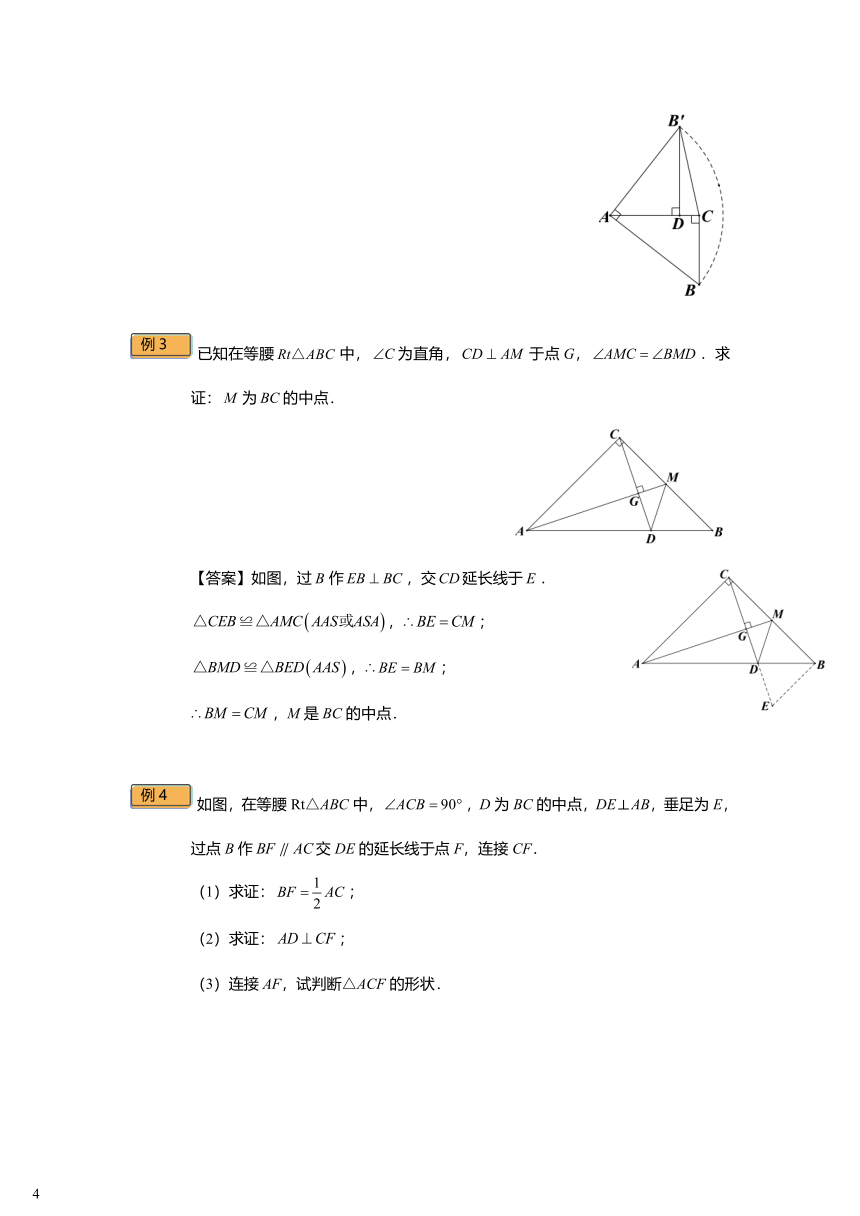
已知在等腰中,为直角,于点G,.求证:为的中点.
【答案】如图,过作,交延长线于.
,∴;
,∴;
∴,M是BC的中点.
如图,在等腰Rt△ABC中,,D为BC的中点,DE⊥AB,垂足为E,
过点B作交DE的延长线于点F,连接CF.
(1)求证:;
(2)求证:;
(3)连接AF,试判断△ACF的形状.
【答案】(1)是等腰直角三角形,∴;
(2)∵,∴,
又∵,∴,,;
(3)等腰三角形().
三垂直的一般情况:一线三等角
已知CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且.
(1)如图1,若∠BCA=60°,时,线段BE和CF大小关系如何,猜想线段BE、AF和EF之间的数量关系,并证明.
(2)如图2,若时,(1)中的结论是否仍然成立,请说明.
【答案】(1),;(2)成立.
如图,等边中,,点O在BC上,且,动点P从点E沿射线EC以1cm/s的速度运动,连接OP,将线段OP绕点O逆时针旋转120°得到线段OF.设点P运动的时间为t秒,问:
①当t是多少时,?
②当t是多少时,?
③当t是多少时,点F恰好落在射线EB上?
【答案】①如下图①,当时,是等边三角形,所以,秒;
②如下图②,当时,,,,所以秒;
③如下图③,点F在EB上时,则有,,所以 秒.
在中,,的平分线交BC于D.过C点作交
AD于E,交AB于G,过D点作于F,求证:.
【答案】∵,,AD为公共边,∴,
∴,∴AD是CF的中垂线,∴.
如图,在中,是斜边上的高,是的平分线,交 于,于,求证:.
【答案】如图,过作.
∵,,∴.
∵,,∴.
而,∴,∴.
∵,∴.
∵,,
∴,故.
∴,,∴.
(也可以过E作BC的垂线,按照模型来证明.)
如图1,已知ABC是等边三角形,点D是边BC的中点,∠ADE=60°,且DE与∠ACB的外角平分线CE相交于点E.
(1)证明:ADE是等边三角形;
(2)若D是线段BC上(B、C点除外)的任意一点,其他条件不变(如图2),那么(1)的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
(3)若D是BC的延长线上(C点除外)的任意一点,其他条件不变(如图3),那么(1)的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
图1 图2 图3
【答案】(1)过点作交于点,则有,即证;
(2)成立,证明同(1);
(3)成立,过点作交的延长线于点,则有,即
证.
如图,在ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E,AD=5,BE=2,求线段DE的长.
【答案】;
如图,在RtABC中,∠ACB=90°,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.求证:AC=EF.
【答案】求证即可。
如图,中,,,D是AB上任意一点, 交CD延长线于E,于F.求证:.
【答案】三垂直模型,易证:,则,,∴.
(1)如图,在中,,点、、分别在边、、上,且,.图中是否存在和全等的三角形?说明理由.
(2)如图,在等边ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则ADE是____________三角形.
【答案】(1);(2)等边
如图,已知ABC中,∠ACB=90°,CD⊥AB于D,∠ABC的角平分线BE交CD于G,交AC于E,M是CG上一点且满足CM=DG. 求证:EM//AB.
【答案】提示:过点作的垂线
八年级数学兴趣小组展示了他们小组探究的过程和发现的结果,内容如下:
(1)如图1,正三角形ABC中,在AB、AC边上分别取点M、N,使BM=AN,连接BN、CM,发现BN=CM,当M、N改变位置且保持BM=AN时,∠NOC保持不变,请猜测∠NOC的度数:∠NOC=______度.
(2)如图2,正方形ABCD中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、DM,那么AN=DM,且∠DON=_______度.
(3)如图3,正五边形ABCDE中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、EM,那么AN=EM,且∠EON=________度.
(4)在正n边形中,对相邻的三边实施同样的操作过程,也会有类似的结论.请大胆猜测,用一句话概括你的发现:___________________________________________________.
【答案】(1); (2) ;(3) ;(4)以上所求的角正好等于正边形的内角
三垂直模型
(1)如图,已知矩形中,E是AD上的一点,F是AB上的一点,,且,,矩形的周长为32cm,求AE的长.
【答案】6cm.
(2)如图,在中,,,CF交AB于点E,,,若,,求CF的长.
【答案】易证:,∴,.
(3)已知:在中,,,直线经过点,过A点作于,过B作于.当绕点旋转且与线段AB有交点时,请你探究线段、、之间的数量关系.
【答案】分情况讨论:如图2的情况,;
如图3的情况,.
(1)如图1,,且,,且,请按照图中所标注的数据计算图中实线所围成的图形的面积;
(2)如图2,在中,,,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求的面积.
图1 图2
【答案】
(1)过E作EF⊥AC于点F,过D作DH垂直AC于点H,则有,,所以所求图形面积.
(2)过B′作于D,则有,∴,.
已知在等腰中,为直角,于点G,.求证:为的中点.
【答案】如图,过作,交延长线于.
,∴;
,∴;
∴,M是BC的中点.
如图,在等腰Rt△ABC中,,D为BC的中点,DE⊥AB,垂足为E,
过点B作交DE的延长线于点F,连接CF.
(1)求证:;
(2)求证:;
(3)连接AF,试判断△ACF的形状.
【答案】(1)是等腰直角三角形,∴;
(2)∵,∴,
又∵,∴,,;
(3)等腰三角形().
三垂直的一般情况:一线三等角
已知CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且.
(1)如图1,若∠BCA=60°,时,线段BE和CF大小关系如何,猜想线段BE、AF和EF之间的数量关系,并证明.
(2)如图2,若时,(1)中的结论是否仍然成立,请说明.
【答案】(1),;(2)成立.
如图,等边中,,点O在BC上,且,动点P从点E沿射线EC以1cm/s的速度运动,连接OP,将线段OP绕点O逆时针旋转120°得到线段OF.设点P运动的时间为t秒,问:
①当t是多少时,?
②当t是多少时,?
③当t是多少时,点F恰好落在射线EB上?
【答案】①如下图①,当时,是等边三角形,所以,秒;
②如下图②,当时,,,,所以秒;
③如下图③,点F在EB上时,则有,,所以 秒.
在中,,的平分线交BC于D.过C点作交
AD于E,交AB于G,过D点作于F,求证:.
【答案】∵,,AD为公共边,∴,
∴,∴AD是CF的中垂线,∴.
如图,在中,是斜边上的高,是的平分线,交 于,于,求证:.
【答案】如图,过作.
∵,,∴.
∵,,∴.
而,∴,∴.
∵,∴.
∵,,
∴,故.
∴,,∴.
(也可以过E作BC的垂线,按照模型来证明.)
如图1,已知ABC是等边三角形,点D是边BC的中点,∠ADE=60°,且DE与∠ACB的外角平分线CE相交于点E.
(1)证明:ADE是等边三角形;
(2)若D是线段BC上(B、C点除外)的任意一点,其他条件不变(如图2),那么(1)的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
(3)若D是BC的延长线上(C点除外)的任意一点,其他条件不变(如图3),那么(1)的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
图1 图2 图3
【答案】(1)过点作交于点,则有,即证;
(2)成立,证明同(1);
(3)成立,过点作交的延长线于点,则有,即
证.
如图,在ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E,AD=5,BE=2,求线段DE的长.
【答案】;
如图,在RtABC中,∠ACB=90°,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.求证:AC=EF.
【答案】求证即可。
如图,中,,,D是AB上任意一点, 交CD延长线于E,于F.求证:.
【答案】三垂直模型,易证:,则,,∴.
(1)如图,在中,,点、、分别在边、、上,且,.图中是否存在和全等的三角形?说明理由.
(2)如图,在等边ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则ADE是____________三角形.
【答案】(1);(2)等边
如图,已知ABC中,∠ACB=90°,CD⊥AB于D,∠ABC的角平分线BE交CD于G,交AC于E,M是CG上一点且满足CM=DG. 求证:EM//AB.
【答案】提示:过点作的垂线
八年级数学兴趣小组展示了他们小组探究的过程和发现的结果,内容如下:
(1)如图1,正三角形ABC中,在AB、AC边上分别取点M、N,使BM=AN,连接BN、CM,发现BN=CM,当M、N改变位置且保持BM=AN时,∠NOC保持不变,请猜测∠NOC的度数:∠NOC=______度.
(2)如图2,正方形ABCD中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、DM,那么AN=DM,且∠DON=_______度.
(3)如图3,正五边形ABCDE中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、EM,那么AN=EM,且∠EON=________度.
(4)在正n边形中,对相邻的三边实施同样的操作过程,也会有类似的结论.请大胆猜测,用一句话概括你的发现:___________________________________________________.
【答案】(1); (2) ;(3) ;(4)以上所求的角正好等于正边形的内角
