八年级上册第十二章 全等三角形之全等三角形旋转模型(教案)
文档属性
| 名称 | 八年级上册第十二章 全等三角形之全等三角形旋转模型(教案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 10:35:25 | ||
图片预览



文档简介
如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)连接BM,证明:MB平分∠AMD.
(3)取AE、CD的中点分别为点P、Q,连接BP、BQ、PQ,如图2,判断△BPQ的形状,并加以证明.
图1 图2
【答案】
(1)△ABE≌△CBD,∴AE=CD.
(2)作BK⊥AE于K,BJ⊥CD于J.∵△ABE≌△CBD,∴AE=CD,S△ABE=S△CDB,
∴BK=BJ,∴MB平分∠AMD.
△ABP≌△CBQ,所以BP=BQ,∠PBQ=∠ABC=90°,△PBQ是等腰直角三角
形.
已知,如图,点线段上的一点,和是等边三角形,直线、交于点,直线、交于点,连接EF.
求证:(1)是等边三角形;
(2)将绕点按逆时针方向旋转,其它条件不变,在图2中补出符合要求的图形,并判断(1)中的结论是否仍然成立,若不成立,另请证明的形状.
【答案】(1)∴,
∵,∴,∴
∴,∴是等边三角形
(2)如下图:不是等边三角形,是直角三角形.
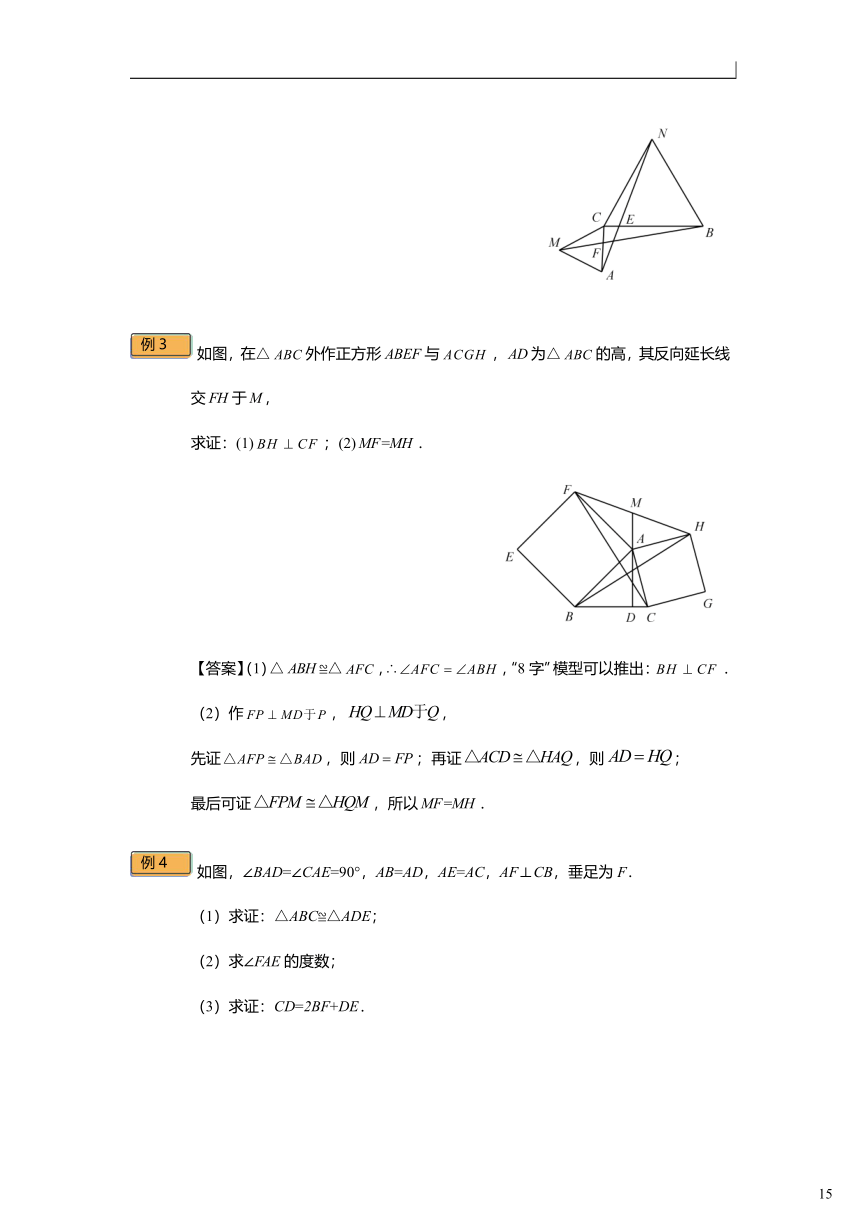
如图,在△外作正方形与,为△的高,其反向延长线交于,
求证:(1);(2).
【答案】(1)△≌△,∴,“8字”模型可以推出:.
(2)作,,
先证,则;再证,则;
最后可证,所以.
如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.
【答案】(1)SAS证全等;(2)135°;(3)延长BF到G,使得FG=FB;
则有△AFB≌△AFG,△ACG≌△ACD,∴CD=CG=BC+2BF=DE+2BF.
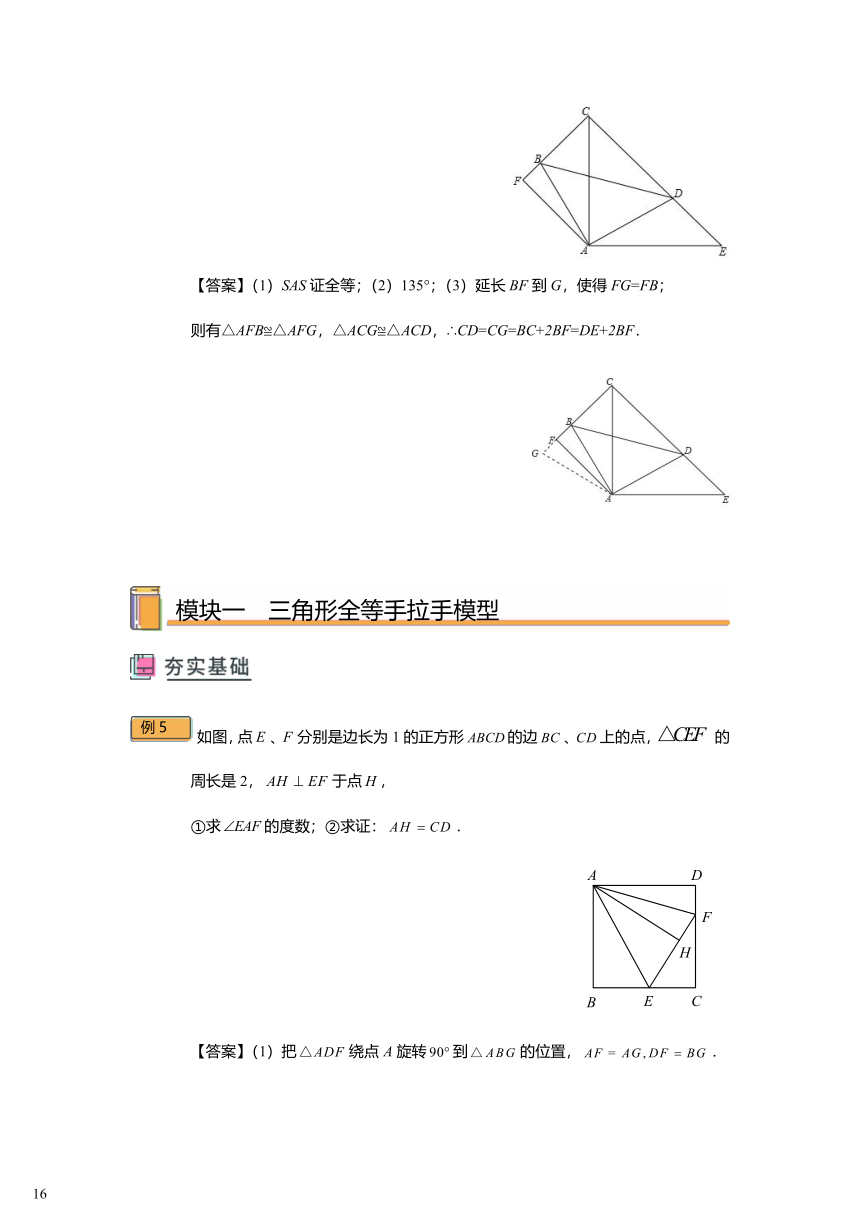
如图,点、分别是边长为1的正方形的边、上的点, 的周长是2,于点,
①求的度数;②求证:.
【答案】(1)把绕点旋转到的位置,.
∵,,∴,,
∴.
全等三角形的对应高相等(利用三角形全等可证得,则有,∴.
(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且,求证:EF=BE+FD;
(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且,(1)中的结论是否仍然成立?
(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
【答案】(1)延长EB到G,使BG=DF,连接AG.则有,∴,EF=BE+FD.
(2)成立;
(3)不成立,应该是
在上截取,使,连接.
则有,∴.
∴,∴.
∵,∴,∴,∵,∴.
五边形中,,,,求证:平分.
【答案】延长至,使得,连接,
∵,,∴,
∵,,∴,∴,,
∵,∴,∴,∴,平分.
如图1,是等腰直角斜边的中点,,、分别交直线、于点、,连接EF.
(1)当绕点D转动时,求证;
(2)如图1,试问、、有怎样的数量关系,请证明;
(3)当旋转到如图2所示的位置时,(2)中的结论是否仍然成立,请说明.
【答案】如图,连结.
(1)则有,∴;
(2);(3)
已知:如图,、、都是等边三角形,且、、共线,.求证:也是等边三角形.
【答案】连接、,则有:,;,;
∵,∴,可证得:,∴;
最后证得,∴,是等边三角形.
如图所示,是边长为的正三角形,是顶角为的等腰三角形,以为顶点作一个的,点、分别在、上,求的周长.
【答案】如图所示,延长到使.
在与中,因为,,,
所以,故.
因为,,所以.
又因为,所以.
在与中,,,,
所以,则,所以的周长为.
已知:如图,点为线段上一点,、是等边三角形.、 分别是、 的高.求证:.
【答案】由,利用进而再证,可得到.
以的两边为边向外作正方形,求证:,且.
【答案】易证,故,又,,故.
如图,等腰直角三角形中,,,为中点,.求证:为定值.
【答案】连结由上可知,,,,
而,.
∴,
∴,
∴.
一位同学拿了两块的三角尺、做了一个探究活动:将的直角顶点放在的斜边的中点处,设.
(1)如图1,两个三角尺的重叠部分为,则重叠部分的面积为 ;
(2)将图1中的绕顶点M逆时针旋转,得到图2,此时重叠部分的面积为 ;
(3)如果将绕旋转到不同于图1、图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.
【答案】(1);
(2);
(3)猜想:重叠部分的面积为
理由如下:过点分别做的垂线,垂足为。
为说明方便,不妨设与的交点为,与的交点为。
由于是斜边的中点,,
所以,
又因为,
所以
因此阴影部分的面积等于正方形的面积。
而正方形的面积是
所以阴影部分的面积是。
(1)求证:AE=CD;
(2)连接BM,证明:MB平分∠AMD.
(3)取AE、CD的中点分别为点P、Q,连接BP、BQ、PQ,如图2,判断△BPQ的形状,并加以证明.
图1 图2
【答案】
(1)△ABE≌△CBD,∴AE=CD.
(2)作BK⊥AE于K,BJ⊥CD于J.∵△ABE≌△CBD,∴AE=CD,S△ABE=S△CDB,
∴BK=BJ,∴MB平分∠AMD.
△ABP≌△CBQ,所以BP=BQ,∠PBQ=∠ABC=90°,△PBQ是等腰直角三角
形.
已知,如图,点线段上的一点,和是等边三角形,直线、交于点,直线、交于点,连接EF.
求证:(1)是等边三角形;
(2)将绕点按逆时针方向旋转,其它条件不变,在图2中补出符合要求的图形,并判断(1)中的结论是否仍然成立,若不成立,另请证明的形状.
【答案】(1)∴,
∵,∴,∴
∴,∴是等边三角形
(2)如下图:不是等边三角形,是直角三角形.
如图,在△外作正方形与,为△的高,其反向延长线交于,
求证:(1);(2).
【答案】(1)△≌△,∴,“8字”模型可以推出:.
(2)作,,
先证,则;再证,则;
最后可证,所以.
如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.
【答案】(1)SAS证全等;(2)135°;(3)延长BF到G,使得FG=FB;
则有△AFB≌△AFG,△ACG≌△ACD,∴CD=CG=BC+2BF=DE+2BF.
如图,点、分别是边长为1的正方形的边、上的点, 的周长是2,于点,
①求的度数;②求证:.
【答案】(1)把绕点旋转到的位置,.
∵,,∴,,
∴.
全等三角形的对应高相等(利用三角形全等可证得,则有,∴.
(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且,求证:EF=BE+FD;
(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且,(1)中的结论是否仍然成立?
(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
【答案】(1)延长EB到G,使BG=DF,连接AG.则有,∴,EF=BE+FD.
(2)成立;
(3)不成立,应该是
在上截取,使,连接.
则有,∴.
∴,∴.
∵,∴,∴,∵,∴.
五边形中,,,,求证:平分.
【答案】延长至,使得,连接,
∵,,∴,
∵,,∴,∴,,
∵,∴,∴,∴,平分.
如图1,是等腰直角斜边的中点,,、分别交直线、于点、,连接EF.
(1)当绕点D转动时,求证;
(2)如图1,试问、、有怎样的数量关系,请证明;
(3)当旋转到如图2所示的位置时,(2)中的结论是否仍然成立,请说明.
【答案】如图,连结.
(1)则有,∴;
(2);(3)
已知:如图,、、都是等边三角形,且、、共线,.求证:也是等边三角形.
【答案】连接、,则有:,;,;
∵,∴,可证得:,∴;
最后证得,∴,是等边三角形.
如图所示,是边长为的正三角形,是顶角为的等腰三角形,以为顶点作一个的,点、分别在、上,求的周长.
【答案】如图所示,延长到使.
在与中,因为,,,
所以,故.
因为,,所以.
又因为,所以.
在与中,,,,
所以,则,所以的周长为.
已知:如图,点为线段上一点,、是等边三角形.、 分别是、 的高.求证:.
【答案】由,利用进而再证,可得到.
以的两边为边向外作正方形,求证:,且.
【答案】易证,故,又,,故.
如图,等腰直角三角形中,,,为中点,.求证:为定值.
【答案】连结由上可知,,,,
而,.
∴,
∴,
∴.
一位同学拿了两块的三角尺、做了一个探究活动:将的直角顶点放在的斜边的中点处,设.
(1)如图1,两个三角尺的重叠部分为,则重叠部分的面积为 ;
(2)将图1中的绕顶点M逆时针旋转,得到图2,此时重叠部分的面积为 ;
(3)如果将绕旋转到不同于图1、图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.
【答案】(1);
(2);
(3)猜想:重叠部分的面积为
理由如下:过点分别做的垂线,垂足为。
为说明方便,不妨设与的交点为,与的交点为。
由于是斜边的中点,,
所以,
又因为,
所以
因此阴影部分的面积等于正方形的面积。
而正方形的面积是
所以阴影部分的面积是。
