八年级上册第十二章 全等三角形之全等三角形构造模型(教案)
文档属性
| 名称 | 八年级上册第十二章 全等三角形之全等三角形构造模型(教案) |  | |
| 格式 | zip | ||
| 文件大小 | 411.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 10:37:34 | ||
图片预览



文档简介
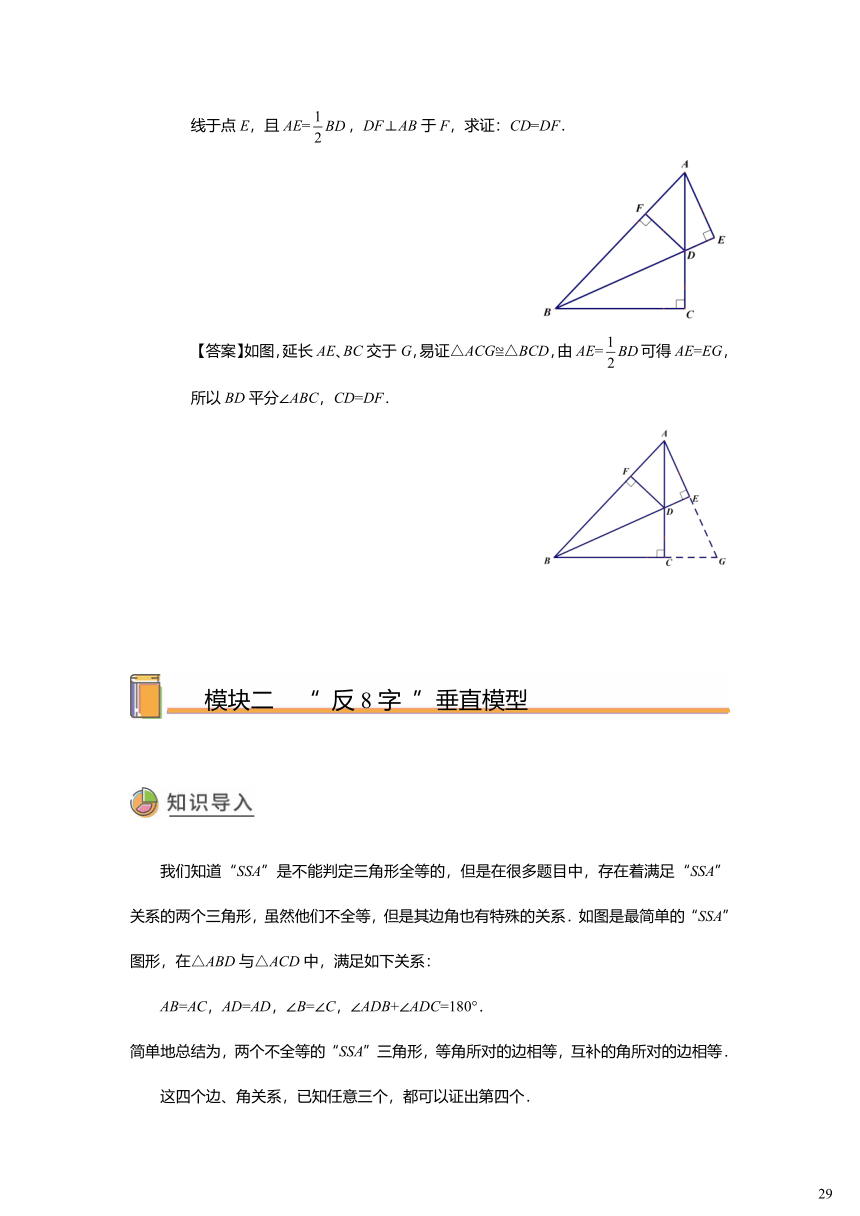
常见的“反8字”垂直模型:
“反8字”垂直模型是一个导角模型,利用互余关系导角要熟练掌握.
如图,在等腰RtABC中,∠ACB=90°,点D是AC上一点,过点A作BD的垂线交BD的延长线于点E,交BC的延长线于F,且BD=2AE.
(1)若,,求的长是多少.
(2)求证:BD平分∠ABC.
【答案】(1)“8字”垂直模型得到:,,∴,,那么;
由(1)得到,所以E是AF的中点,,∴BD平分∠ABC.
如图,ABC的两条高AD、BE相交于点G,CG的延长线交AB于点F,BG=AC.求证:BF=FC.
【答案】“8字”垂直模型得到:,,∴DG=DC,∠FCB=45°,
∴BD=AD,∠ABD=45°,∴BF=FC.
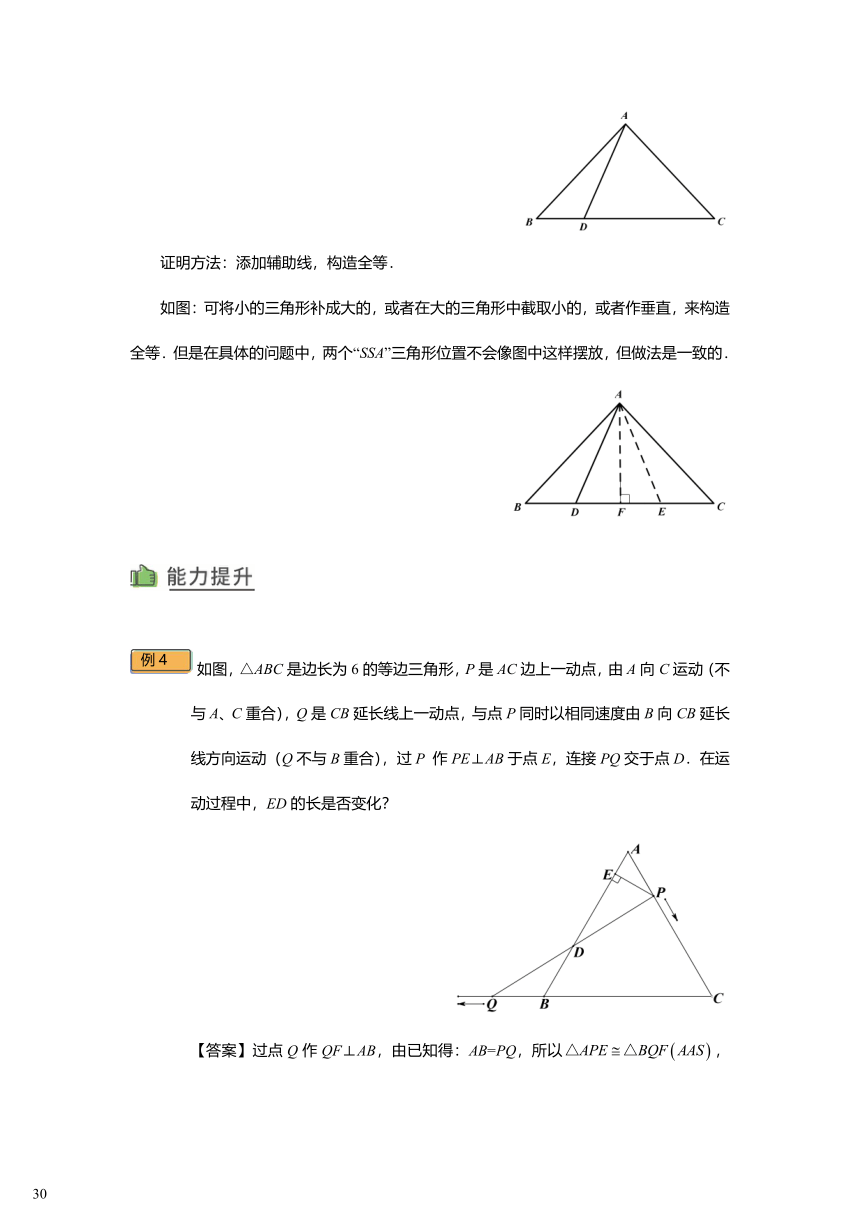
如图,在ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于点E,且AE=,DF⊥AB于F,求证:CD=DF.
【答案】如图,延长AE、BC交于G,易证△ACG≌△BCD,由AE=可得AE=EG,
所以BD平分∠ABC,CD=DF.
我们知道“SSA”是不能判定三角形全等的,但是在很多题目中,存在着满足“SSA”关系的两个三角形,虽然他们不全等,但是其边角也有特殊的关系.如图是最简单的“SSA”图形,在△ABD与△ACD中,满足如下关系:
AB=AC,AD=AD,∠B=∠C,∠ADB+∠ADC=180°.
简单地总结为,两个不全等的“SSA”三角形,等角所对的边相等,互补的角所对的边相等.
这四个边、角关系,已知任意三个,都可以证出第四个.
证明方法:添加辅助线,构造全等.
如图:可将小的三角形补成大的,或者在大的三角形中截取小的,或者作垂直,来构造全等.但是在具体的问题中,两个“SSA”三角形位置不会像图中这样摆放,但做法是一致的.
如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(不与A、C重合),Q是CB延长线上一动点,与点P同时以相同速度由B向CB延长线方向运动(Q不与B重合),过P 作PE⊥AB于点E,连接PQ交于点D.在运动过程中,ED的长是否变化?
【答案】过点Q作QF⊥AB,由已知得:AB=PQ,所以,PE=QF,所以,∴DE=DF,总上可得:,是定值.
如图,∠A=60°,∠DBC=∠ECB=30°,BD与CE交于点O,求证:BE=CD
【答案】△BOE和△COD中,OB=OC,∠BOE=∠COD,由四边形内角和可推出∠BEO+∠CDO=180°,
如果延长CE到F,使OF=OD,易证△OCD≌△OBF,△BEF是等腰三角形,BF=BE,所以BE=CD.
(也可以在OD上截取OM=OE;或者分别过B、C作CE、BD的垂线,也可以证明.)
构造等边三角形
(1)在等腰直角△ABC中,∠BAC=90°,点D为射线BC上一动点,连接AD,以AD为直角边作等腰直角△ADF,且∠DAF=90°.如图1,当点D在线段BC上时,CF=BD且CF⊥BD.
请问:当点D在线段BC的延长线上且在AD左侧作等腰直角△ADF时,CF与BD有怎样的数量和位置关系?请在图2中作图并证明.
(2)如图3,若AB≠AC,∠BAC≠90°,∠BCA=45°.点D在线段BC上运动,试探究CF与BC的位置关系.
图1 图2
图3
【答案】(1)①CF=BD,CF⊥BD;②成立
(2)CF⊥BC,如图做AM⊥AC即可.
在等边△ABC中:
(1)如图1,P为等边△ABC外一点,且∠BPC=120°,求证:PA=PB+PC.
(2)如图2,P为等边△ABC内一点,且∠APD=120°,求证:PA+PD+PC>BD.
图1 图2
【答案】(1)如图延长BP到D,使PD=CP,易证△PCD是等边三角形,则△ACP≌△BCD,则PA=PB+PC.
(2)同(1)一样,构造等边三角形手拉手模型,延长DP到M使AP=PM,连接AM、MB,则△AMP是等边三角形,易证△AMB≌△APC.MB=PC,∵MB+MD>BD,∴PA+PD+PC>BD.
在正方形ABCD内部,∠EAF=45°,∠ECF=45°,求证:BE∥DF.
【答案】如图将△BCE绕点C顺时针旋转90°到△DCH,将△AEB绕点A逆时针旋转90°到△AGD,
连接EF、FG、FH,通过全等可得:FH=EF,GF=EF,所以FH=FG,同样的DH=BE,DG=BE,所以DH=DG,通过平角可得:DH和DG共线,所以DF⊥DH,而BE⊥DH(旋转角为90°),所以BE∥DF.
(1)如图所示的△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.则△ABC的面积是 .
如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.则
AF和CD的数量关系是 .
【答案】(1)由全等可得AE=BE=4,CE=EM=3,所以面积=14.
(2)AF=2CD.
如图,在△ABC中,AC=BC,∠ACB=90°,D是AC上一点,AE⊥BD,交BD的延长线于E,并且AE=,求证:BD平分∠ABC.
【答案】延长AE、BC相交于点F,△ACF≌△BCD,结合已知可得:E是AF中点,BE是AF的中垂线,
∴BD平分∠ABC.
如图,在等腰△ABC中,延长AC到E,使CE=BD,DE交BC于F.求证:DF=FE.
【答案】如图过D做DG∥AE,易证BD=DG=CE,所以△CEF≌△GDF,DF=FE.
(或者过E作EG∥AB交BC延长线于点G,
或者过点D作DM⊥BC,过点E作EN⊥BC,均可证明)
Rt△ABC中,∠ACB=90°,AC=BC,点E为△ABC外一点,且∠CEA=45°.
求证:AE⊥BE.
【答案】如图过C点作CF⊥CE交EA的延长线于F,则有是等腰直角三角形,,所以,,AE⊥BE.
如图,△ABC是等边三角形,,求证:.
【答案】延长AD到E,使得,易得是正三角形,
于是可得,所以.
“反8字”垂直模型是一个导角模型,利用互余关系导角要熟练掌握.
如图,在等腰RtABC中,∠ACB=90°,点D是AC上一点,过点A作BD的垂线交BD的延长线于点E,交BC的延长线于F,且BD=2AE.
(1)若,,求的长是多少.
(2)求证:BD平分∠ABC.
【答案】(1)“8字”垂直模型得到:,,∴,,那么;
由(1)得到,所以E是AF的中点,,∴BD平分∠ABC.
如图,ABC的两条高AD、BE相交于点G,CG的延长线交AB于点F,BG=AC.求证:BF=FC.
【答案】“8字”垂直模型得到:,,∴DG=DC,∠FCB=45°,
∴BD=AD,∠ABD=45°,∴BF=FC.
如图,在ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于点E,且AE=,DF⊥AB于F,求证:CD=DF.
【答案】如图,延长AE、BC交于G,易证△ACG≌△BCD,由AE=可得AE=EG,
所以BD平分∠ABC,CD=DF.
我们知道“SSA”是不能判定三角形全等的,但是在很多题目中,存在着满足“SSA”关系的两个三角形,虽然他们不全等,但是其边角也有特殊的关系.如图是最简单的“SSA”图形,在△ABD与△ACD中,满足如下关系:
AB=AC,AD=AD,∠B=∠C,∠ADB+∠ADC=180°.
简单地总结为,两个不全等的“SSA”三角形,等角所对的边相等,互补的角所对的边相等.
这四个边、角关系,已知任意三个,都可以证出第四个.
证明方法:添加辅助线,构造全等.
如图:可将小的三角形补成大的,或者在大的三角形中截取小的,或者作垂直,来构造全等.但是在具体的问题中,两个“SSA”三角形位置不会像图中这样摆放,但做法是一致的.
如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(不与A、C重合),Q是CB延长线上一动点,与点P同时以相同速度由B向CB延长线方向运动(Q不与B重合),过P 作PE⊥AB于点E,连接PQ交于点D.在运动过程中,ED的长是否变化?
【答案】过点Q作QF⊥AB,由已知得:AB=PQ,所以,PE=QF,所以,∴DE=DF,总上可得:,是定值.
如图,∠A=60°,∠DBC=∠ECB=30°,BD与CE交于点O,求证:BE=CD
【答案】△BOE和△COD中,OB=OC,∠BOE=∠COD,由四边形内角和可推出∠BEO+∠CDO=180°,
如果延长CE到F,使OF=OD,易证△OCD≌△OBF,△BEF是等腰三角形,BF=BE,所以BE=CD.
(也可以在OD上截取OM=OE;或者分别过B、C作CE、BD的垂线,也可以证明.)
构造等边三角形
(1)在等腰直角△ABC中,∠BAC=90°,点D为射线BC上一动点,连接AD,以AD为直角边作等腰直角△ADF,且∠DAF=90°.如图1,当点D在线段BC上时,CF=BD且CF⊥BD.
请问:当点D在线段BC的延长线上且在AD左侧作等腰直角△ADF时,CF与BD有怎样的数量和位置关系?请在图2中作图并证明.
(2)如图3,若AB≠AC,∠BAC≠90°,∠BCA=45°.点D在线段BC上运动,试探究CF与BC的位置关系.
图1 图2
图3
【答案】(1)①CF=BD,CF⊥BD;②成立
(2)CF⊥BC,如图做AM⊥AC即可.
在等边△ABC中:
(1)如图1,P为等边△ABC外一点,且∠BPC=120°,求证:PA=PB+PC.
(2)如图2,P为等边△ABC内一点,且∠APD=120°,求证:PA+PD+PC>BD.
图1 图2
【答案】(1)如图延长BP到D,使PD=CP,易证△PCD是等边三角形,则△ACP≌△BCD,则PA=PB+PC.
(2)同(1)一样,构造等边三角形手拉手模型,延长DP到M使AP=PM,连接AM、MB,则△AMP是等边三角形,易证△AMB≌△APC.MB=PC,∵MB+MD>BD,∴PA+PD+PC>BD.
在正方形ABCD内部,∠EAF=45°,∠ECF=45°,求证:BE∥DF.
【答案】如图将△BCE绕点C顺时针旋转90°到△DCH,将△AEB绕点A逆时针旋转90°到△AGD,
连接EF、FG、FH,通过全等可得:FH=EF,GF=EF,所以FH=FG,同样的DH=BE,DG=BE,所以DH=DG,通过平角可得:DH和DG共线,所以DF⊥DH,而BE⊥DH(旋转角为90°),所以BE∥DF.
(1)如图所示的△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.则△ABC的面积是 .
如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.则
AF和CD的数量关系是 .
【答案】(1)由全等可得AE=BE=4,CE=EM=3,所以面积=14.
(2)AF=2CD.
如图,在△ABC中,AC=BC,∠ACB=90°,D是AC上一点,AE⊥BD,交BD的延长线于E,并且AE=,求证:BD平分∠ABC.
【答案】延长AE、BC相交于点F,△ACF≌△BCD,结合已知可得:E是AF中点,BE是AF的中垂线,
∴BD平分∠ABC.
如图,在等腰△ABC中,延长AC到E,使CE=BD,DE交BC于F.求证:DF=FE.
【答案】如图过D做DG∥AE,易证BD=DG=CE,所以△CEF≌△GDF,DF=FE.
(或者过E作EG∥AB交BC延长线于点G,
或者过点D作DM⊥BC,过点E作EN⊥BC,均可证明)
Rt△ABC中,∠ACB=90°,AC=BC,点E为△ABC外一点,且∠CEA=45°.
求证:AE⊥BE.
【答案】如图过C点作CF⊥CE交EA的延长线于F,则有是等腰直角三角形,,所以,,AE⊥BE.
如图,△ABC是等边三角形,,求证:.
【答案】延长AD到E,使得,易得是正三角形,
于是可得,所以.
