八年级下册第十八章 平行四边形18.1 平行四边形第01讲平行四边形(教案)
文档属性
| 名称 | 八年级下册第十八章 平行四边形18.1 平行四边形第01讲平行四边形(教案) |
|
|
| 格式 | zip | ||
| 文件大小 | 420.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 00:00:00 | ||
图片预览


文档简介
第1话:平行四边形
课堂思维碰撞
第一层:平行四边形的性质
知识导入
1.平行四边形有关的概念
平行四边形的定义:两组对边分别平行的四边形是平行四边形.平行四边形可用“”表示.
对角线:平行四边形不相邻的两个顶点连成的线段叫做它的对角线.
例:如图,平行四边形可表示为或,BD、AC为对角线
注意:字母代表顺序性
2.平行四边形的性质
性质 图解
边 ①两组对边分别平行且相等 ①, ②,, ③, ④ ⑤,
角 ②对角相等,邻角互补
对角线 ③对角线互相平分 ④分成的四个小三角形面积相等, 其中两对小三角形全等 ⑤对角线交点为平行四边形对称中心
周长 ①周长=邻边之和×2 ① ②
面积 ②面积=底×高
对称中心 ①过对称中心的直线把平行四边形分成全等两部分 ②过对称中心的直线平分平行四边形的面积和周长 ① ②
角分线 ①任一角分线与边相交成等腰三角形 ②邻角角分线互相垂直 ①为等腰三角形 ②
平行四边形中面积一半问题:
点在边上 点在内部 点在外部
夯实基础
例1 平行四边形基本性质
(1) 如图,在平行四边形中,剪去大小不同的平行四边形,得到另两个图形,将三个图形分别标上、、,记周长分别为、、,则必有( )
A. B. C. D.无法确定
(2)如图,已知等边三角形的边长为,是内一点,,,点
分别在上,则
(3)已知平行四边形相邻两角的度数比为,则较大的角为( )
A. B. C. D.
(4)如图,在平行四边形中,,,于,则 .
(5)如图, ABCD的CD边上有一点E,连接AE、BE,∠DAE=12°,∠AEB=33°,则∠EBC的度数是( )
A.18° B.21° C.33° D.45°
(6)如图,□ABCD中,和的周长分别为10和14,且平行四边形的周长为22,则对角线的长度之和为_______,和的长分别为_________.
【答案】(1)C;(2)10;(3)C;(4);(5)B;(6)13、3.5、7.5;
能力提升
例2 平行四边形模型
(1)如图,在 ABCD中,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,若△CED的周长为6,则 ABCD的周长为( )
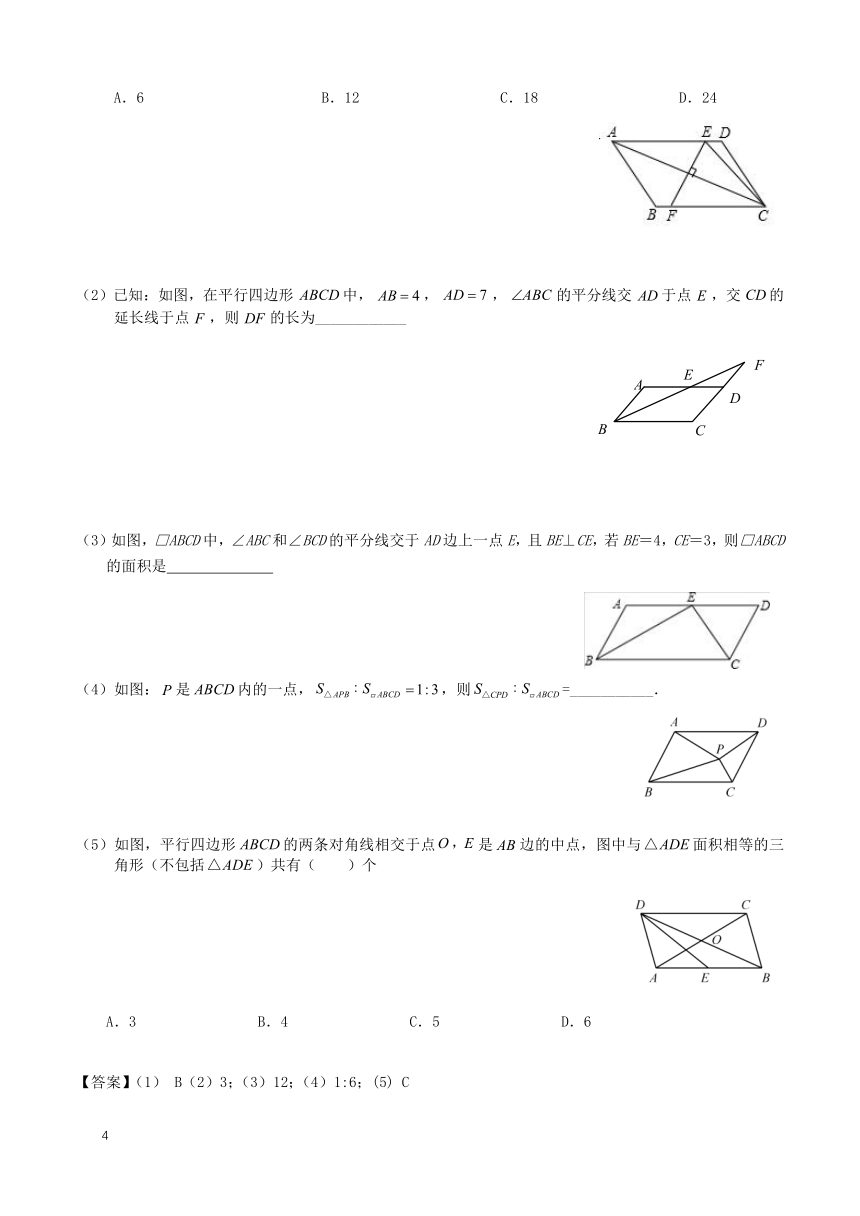
A.6 B.12 C.18 D.24
(2)已知:如图,在平行四边形中,,,的平分线交于点,交的延长线于点,则的长为____________
(3)如图,□ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE⊥CE,若BE=4,CE=3,则□ABCD的面积是
(4)如图:是内的一点,,则=___________.
(5)如图,平行四边形的两条对角线相交于点是边的中点,图中与面积相等的三角形(不包括)共有( )个
A.3 B.4 C.5 D.6
【答案】(1) B(2)3;(3)12;(4)1:6;(5) C
例3 中心对称
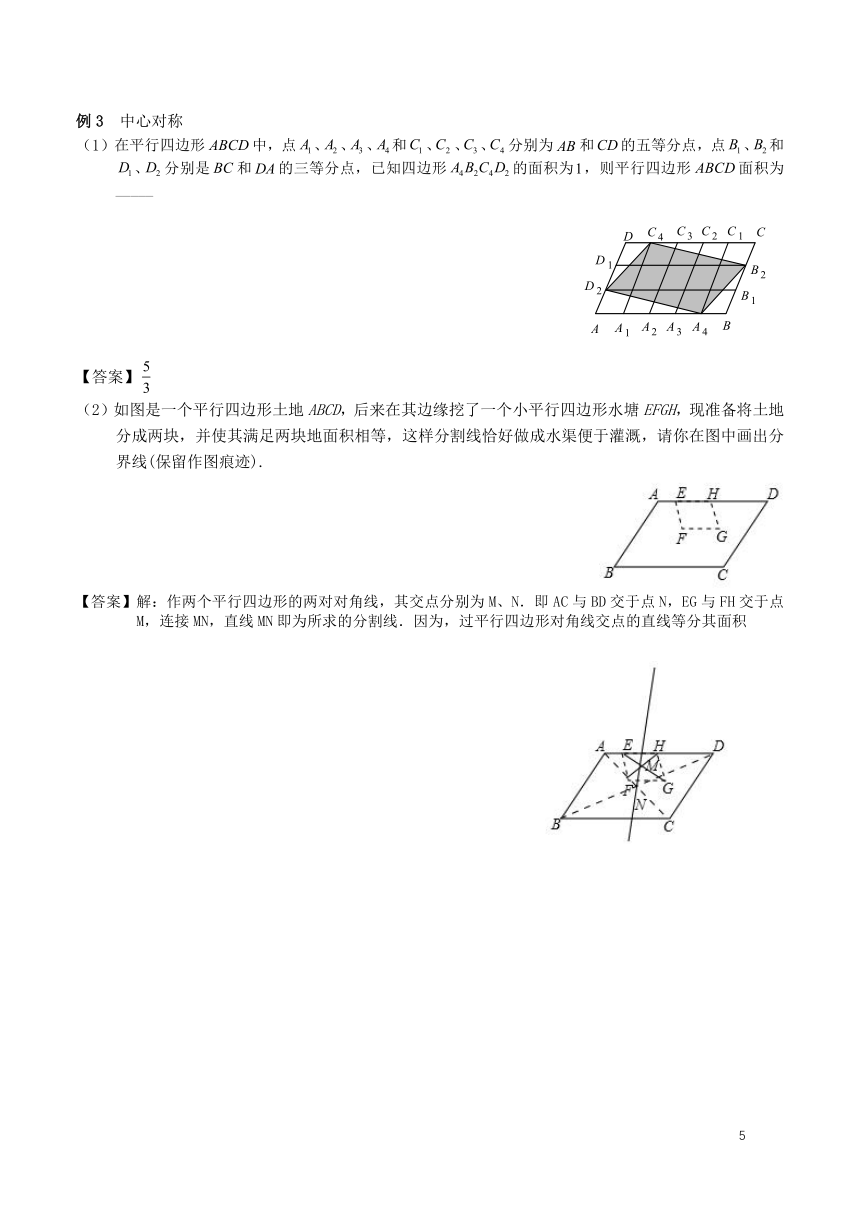
(1)在平行四边形中,点、、、和、、、分别为和的五等分点,点、和、分别是和的三等分点,已知四边形的面积为,则平行四边形面积为_____
【答案】
(2)如图是一个平行四边形土地ABCD,后来在其边缘挖了一个小平行四边形水塘EFGH,现准备将土地分成两块,并使其满足两块地面积相等,这样分割线恰好做成水渠便于灌溉,请你在图中画出分界线(保留作图痕迹).
【答案】解:作两个平行四边形的两对对角线,其交点分别为M、N.即AC与BD交于点N,EG与FH交于点M,连接MN,直线MN即为所求的分割线.因为,过平行四边形对角线交点的直线等分其面积
第二层:平行四边形的判定
知识导入
判定定理 几何语言
边 ①两组对边分别平行的四边形为平行四边形 ① ② ③ ④ ⑤
②两组对边分别相等的四边形为平行四边形
③一组对边平行且相等的四边形为平行四边形
角 ④两组对角分别相等的四边形为平行四边形
对角线 ⑤对角线互相平分的四边形为平行四边形
能力提升
例4 平行四边形的判定
已知,如图,四边形是平行四边形,平分交于点,平分交于点.求证:四边形是平行四边形.
①利用两组对角分别相等判定
②利用一组对边平行且相等判定
【答案】①易证,同理,,得,通过补角性质得到,从而证到平行四边形②易证AE=AB=CD=CF,则BF=ED,BF∥ED,从而证到平行四边形。
例5如图,在平行四边形中,点、在上,且.
⑴求证:;
⑵延长交的延长线于,延长交的延长线于(请补全图形),证明四边形是平行四边形.
【答案】(1)解:∵AD∥BC,∴∠ADE=∠CBF
由AD=CB,BF=DE,∠ADE=∠CBF;
可证
(2)证明:△ADE≌△CBF,
∴∠AED=∠CFB.
∵∠FEG=∠AED=∠CFB=∠EFH,
∴AG‖HC,而且,AH‖GC,
∴四边形AGCH是平行四边形
例6 如图所示,以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD、△BCE、△ACF,
猜想:四边形ADEF是什么四边形,试证明你的结论
【答案】证明:四边形ADEF是平行四边形.
连接ED、EF,
∵△ABD、△BCE、△ACF分别是等边三角形,
∴AB=BD,BC=BE,∠DBA=∠EBC=60°.
∴∠DBE=∠ABC.
∴△ABC≌△DBE.
同理可证△ABC≌△FEC,
∴AB=EF,AC=DE.
∵AB=AD,AC=AF,
∴AD=EF,DE=AF.
∴四边形ADEF是平行四边形.
横扫学霸
例7 如图,四边形的对角线、交于点,过点作直线交于点,交于点.若,且.求证:四边形是平行四边形.
【答案】证明:延长AC,在C上方取N,A下方取M,使AM=AE,CN=CF,则由已知可得PM=PN,
易证△PME≌△PNF,且△AME,△CNF都是等腰三角形.
∴∠M=∠N,∠MEP=∠NFP
∴∠AEP=∠PFC
∴AD∥BC,
可证得△PAE≌△PCF,得PA=PC,
再证△PED≌△PFB.得PB=PD.
∴ABCD为平行四边形
课后创新培养
课后作业
练1
(1) 平行四边形中一边的长为10cm,那么它的两条对角线的长度可能是( )
A.4cm和6cm B.20cm和30cm C.6cm和8cm D.8cm和12cm
【答案】B
(2)在平行四边形中,,延长至,延长至,连接,则( )
A. B. C. D.
【答案】D
(3)如图,EF过 ABCD对角线的交点O,交AD于E,交BC于F,若 ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )
A.14 B.13 C.12 D.10
【答案】C
练2 如图,在平行四边形中,是的平分线,是的中点,,
,则为( )
A. B. C. D.
【答案】
练3 已知四边形中,、交于点,给出条件①且,②且,③且,④且,其中能判定四边形是平行四边形的有( )
A.0个 B.1个 C.2个 D.3个
【答案】A
练4 已知,如图,,且,为的中点,求证:
【答案】证明思路:易证四边形为平行四边形,得到
练5 现有如图2的铁片,其形状是一个大的平行四边形在一角剪去一个小的平行四边形,工人师傅想用一条直线将其分割成面积相等的两部分,请你帮助师傅设计三种不同的分割方案.
【答案】
10
7
课堂思维碰撞
第一层:平行四边形的性质
知识导入
1.平行四边形有关的概念
平行四边形的定义:两组对边分别平行的四边形是平行四边形.平行四边形可用“”表示.
对角线:平行四边形不相邻的两个顶点连成的线段叫做它的对角线.
例:如图,平行四边形可表示为或,BD、AC为对角线
注意:字母代表顺序性
2.平行四边形的性质
性质 图解
边 ①两组对边分别平行且相等 ①, ②,, ③, ④ ⑤,
角 ②对角相等,邻角互补
对角线 ③对角线互相平分 ④分成的四个小三角形面积相等, 其中两对小三角形全等 ⑤对角线交点为平行四边形对称中心
周长 ①周长=邻边之和×2 ① ②
面积 ②面积=底×高
对称中心 ①过对称中心的直线把平行四边形分成全等两部分 ②过对称中心的直线平分平行四边形的面积和周长 ① ②
角分线 ①任一角分线与边相交成等腰三角形 ②邻角角分线互相垂直 ①为等腰三角形 ②
平行四边形中面积一半问题:
点在边上 点在内部 点在外部
夯实基础
例1 平行四边形基本性质
(1) 如图,在平行四边形中,剪去大小不同的平行四边形,得到另两个图形,将三个图形分别标上、、,记周长分别为、、,则必有( )
A. B. C. D.无法确定
(2)如图,已知等边三角形的边长为,是内一点,,,点
分别在上,则
(3)已知平行四边形相邻两角的度数比为,则较大的角为( )
A. B. C. D.
(4)如图,在平行四边形中,,,于,则 .
(5)如图, ABCD的CD边上有一点E,连接AE、BE,∠DAE=12°,∠AEB=33°,则∠EBC的度数是( )
A.18° B.21° C.33° D.45°
(6)如图,□ABCD中,和的周长分别为10和14,且平行四边形的周长为22,则对角线的长度之和为_______,和的长分别为_________.
【答案】(1)C;(2)10;(3)C;(4);(5)B;(6)13、3.5、7.5;
能力提升
例2 平行四边形模型
(1)如图,在 ABCD中,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,若△CED的周长为6,则 ABCD的周长为( )
A.6 B.12 C.18 D.24
(2)已知:如图,在平行四边形中,,,的平分线交于点,交的延长线于点,则的长为____________
(3)如图,□ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE⊥CE,若BE=4,CE=3,则□ABCD的面积是
(4)如图:是内的一点,,则=___________.
(5)如图,平行四边形的两条对角线相交于点是边的中点,图中与面积相等的三角形(不包括)共有( )个
A.3 B.4 C.5 D.6
【答案】(1) B(2)3;(3)12;(4)1:6;(5) C
例3 中心对称
(1)在平行四边形中,点、、、和、、、分别为和的五等分点,点、和、分别是和的三等分点,已知四边形的面积为,则平行四边形面积为_____
【答案】
(2)如图是一个平行四边形土地ABCD,后来在其边缘挖了一个小平行四边形水塘EFGH,现准备将土地分成两块,并使其满足两块地面积相等,这样分割线恰好做成水渠便于灌溉,请你在图中画出分界线(保留作图痕迹).
【答案】解:作两个平行四边形的两对对角线,其交点分别为M、N.即AC与BD交于点N,EG与FH交于点M,连接MN,直线MN即为所求的分割线.因为,过平行四边形对角线交点的直线等分其面积
第二层:平行四边形的判定
知识导入
判定定理 几何语言
边 ①两组对边分别平行的四边形为平行四边形 ① ② ③ ④ ⑤
②两组对边分别相等的四边形为平行四边形
③一组对边平行且相等的四边形为平行四边形
角 ④两组对角分别相等的四边形为平行四边形
对角线 ⑤对角线互相平分的四边形为平行四边形
能力提升
例4 平行四边形的判定
已知,如图,四边形是平行四边形,平分交于点,平分交于点.求证:四边形是平行四边形.
①利用两组对角分别相等判定
②利用一组对边平行且相等判定
【答案】①易证,同理,,得,通过补角性质得到,从而证到平行四边形②易证AE=AB=CD=CF,则BF=ED,BF∥ED,从而证到平行四边形。
例5如图,在平行四边形中,点、在上,且.
⑴求证:;
⑵延长交的延长线于,延长交的延长线于(请补全图形),证明四边形是平行四边形.
【答案】(1)解:∵AD∥BC,∴∠ADE=∠CBF
由AD=CB,BF=DE,∠ADE=∠CBF;
可证
(2)证明:△ADE≌△CBF,
∴∠AED=∠CFB.
∵∠FEG=∠AED=∠CFB=∠EFH,
∴AG‖HC,而且,AH‖GC,
∴四边形AGCH是平行四边形
例6 如图所示,以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD、△BCE、△ACF,
猜想:四边形ADEF是什么四边形,试证明你的结论
【答案】证明:四边形ADEF是平行四边形.
连接ED、EF,
∵△ABD、△BCE、△ACF分别是等边三角形,
∴AB=BD,BC=BE,∠DBA=∠EBC=60°.
∴∠DBE=∠ABC.
∴△ABC≌△DBE.
同理可证△ABC≌△FEC,
∴AB=EF,AC=DE.
∵AB=AD,AC=AF,
∴AD=EF,DE=AF.
∴四边形ADEF是平行四边形.
横扫学霸
例7 如图,四边形的对角线、交于点,过点作直线交于点,交于点.若,且.求证:四边形是平行四边形.
【答案】证明:延长AC,在C上方取N,A下方取M,使AM=AE,CN=CF,则由已知可得PM=PN,
易证△PME≌△PNF,且△AME,△CNF都是等腰三角形.
∴∠M=∠N,∠MEP=∠NFP
∴∠AEP=∠PFC
∴AD∥BC,
可证得△PAE≌△PCF,得PA=PC,
再证△PED≌△PFB.得PB=PD.
∴ABCD为平行四边形
课后创新培养
课后作业
练1
(1) 平行四边形中一边的长为10cm,那么它的两条对角线的长度可能是( )
A.4cm和6cm B.20cm和30cm C.6cm和8cm D.8cm和12cm
【答案】B
(2)在平行四边形中,,延长至,延长至,连接,则( )
A. B. C. D.
【答案】D
(3)如图,EF过 ABCD对角线的交点O,交AD于E,交BC于F,若 ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )
A.14 B.13 C.12 D.10
【答案】C
练2 如图,在平行四边形中,是的平分线,是的中点,,
,则为( )
A. B. C. D.
【答案】
练3 已知四边形中,、交于点,给出条件①且,②且,③且,④且,其中能判定四边形是平行四边形的有( )
A.0个 B.1个 C.2个 D.3个
【答案】A
练4 已知,如图,,且,为的中点,求证:
【答案】证明思路:易证四边形为平行四边形,得到
练5 现有如图2的铁片,其形状是一个大的平行四边形在一角剪去一个小的平行四边形,工人师傅想用一条直线将其分割成面积相等的两部分,请你帮助师傅设计三种不同的分割方案.
【答案】
10
7
