八年级下册第十九章 一次函数第03讲 函数初步(教案)
文档属性
| 名称 | 八年级下册第十九章 一次函数第03讲 函数初步(教案) |  | |
| 格式 | zip | ||
| 文件大小 | 360.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 10:45:52 | ||
图片预览



文档简介
第3话:函数初步
课堂思维碰撞
第一层:变量与函数
知识导入
基本概念
变量与常量
在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
自变量与函数
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一的值与其对应,那么我们就说x是自变量,y是x的函数.如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
解析式
用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数常用的方法.这种式子叫做函数的解析式.
注意:
函数不是数,它是指在一个变化过程中两个变量之间的关系,函数本质就是变量间的对应关系.
⑴对于每一个给定的值,有一个唯一确定的值与之对应,否则就不是的函数.例如就不是函数,因为当时,,即有两个值与对应.
⑵对于每一个给定的值,可以有一个值与之对应,也可以有多个值与之对应.例如在函数中,时,;时,.
确定函数自变量取值范围的方法:
(1)整式型:一般取全体实数
(2)分式型:使得分母不为0
(3)根式型:①根指数为偶数时被开方数为非负数
②根指数为奇数时被开方数为任意实数
(4)非正整数幂:底数不为0
(5)整式、分式和根式的组合型:取各自取值范围的公共部分
(6)实际问题:符合实际意义
夯实基础
例1 基本概念
(1)在圆的周长公式C=2πr中,下列说法错误的是( )
A.C,π,r是变量,2是常量
B.C,r是变量,2π是常量
C.r是自变量,C是r的函数
D.将C=2πr写成,则可看作C是自变量,r是C的函数
(2)某品牌豆浆机成本为70元,销售商对其销量定价的关系进行了调查,结果如下( ):
定价(元) 100 110 120 130 140 150
销量(个) 80 100 110 100 80 60
A.定价是常量,销量是变量
B.定价是变量,销量是不变量
C.定价与销售量都是变量,定价是自变量,销量是因变量
D.定价与销量都是变量,销量是自变量,定价是因变量
【答案】(1)A ;(2)C
能力提升
例2
(1)下列式子中,是的函数的有_____________
①;②;③;④;⑤;⑥y=;⑦
(2)下面每个选项中给出了某个变化过程中的两个变量x和y,其中y不是x的函数的选项是( )
A.y:正方形的面积,x:这个正方形的周长
B.y:某班学生的身高,x:这个班学生的学号
C.y:圆的面积,x:这个圆的直径
D.y:一个正数的平方根,x:这个正数
(3)求下列式子中自变量的取值范围.
① ② ③ ④ ⑤
【答案】(1)①②④⑥⑦;(2)D(3)①全体实数;②x≠3;③x≠-1且x≠0;④;
⑤x≥2且x≠3
例3(1) 等腰周长为,底边长为,腰长为.
①写出关于的函数关系式;
②求的取值范围;
③求的取值范围.
【答案】(1)解:①y=10﹣2x;
②∵x>0,y>0,2x>y∴10﹣2x>0,2x>10﹣2x,解得;
③∵x=5﹣∴<5﹣<5,解得0<y<5.
(2)某地市话的收费标准为:
①通话时间在3分钟以内(包括3分钟)话费每分钟0.2元;
②通话时间超过3分钟时,超过部分的话费按每分钟0.15元计算.
那么话费y(元)与通话时间x(分)之间的关系式为_________(写出自变量的取值范围)
【答案】
第二层: 函数的图象
知识导入
1.函数图象的概念:
对于一个函数,如果把自变量和函数的每对值分别作为点的横坐标与纵坐标,在平面直角坐标系内描出相应的点,这些点所组成的图形,就是函数的图象.
2.函数图象的画法
⑴列表; ⑵描点; ⑶连线.
3.函数解析式与函数图象的关系:
由函数图象的定义可知,图象上任意一点中的,都是解析式方程的一个解.反之,以解析式方程的任意一个解为坐标的点一定在函数的图象上.
判断一个点是否在函数图象上的方法是:将这个点的坐标值代入函数的解析式,如果满足函数解析式,这个点就在函数的图象上,否则就不在这个函数的图象上.
夯实基础
例4 函数图象
如图下列各曲线中表示y是x的函数的是( )
A. B. C. D.
【答案】A
能力提升
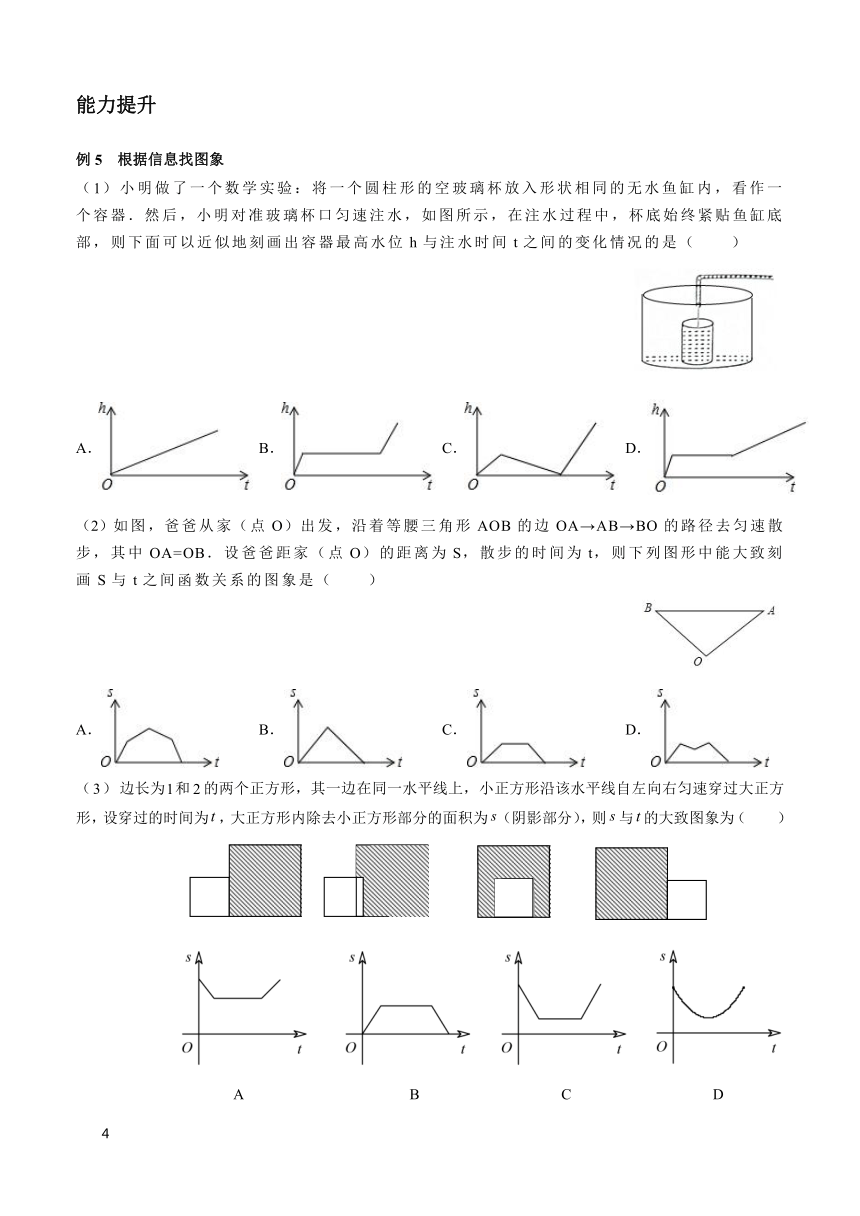
例5 根据信息找图象
(1)小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
A. B. C. D.
(2)如图,爸爸从家(点O)出发,沿着等腰三角形AOB的边OA→AB→BO的路径去匀速散步,其中OA=OB.设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )
A. B. C. D.
(3)边长为和的两个正方形,其一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为,大正方形内除去小正方形部分的面积为(阴影部分),则与的大致图象为( )
A B C D
(4)小刚以400米/分的速度匀速骑车5分,在原地休息了6分,然后以500米/分的速度骑回出发地,下列函数图象能表达这一过程的是( )
A. B. C. D.
【答案】(1)D;(2)D;(3)A;(4)C;
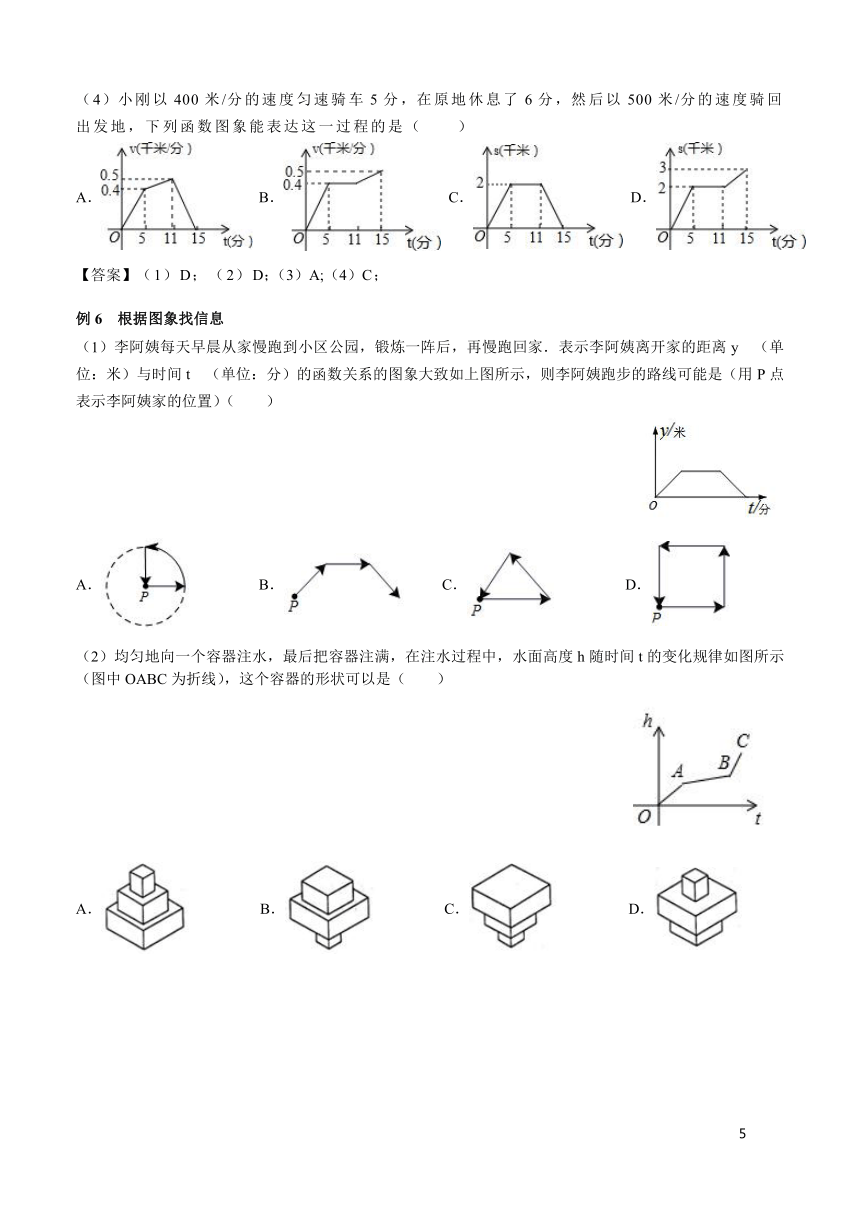
例6 根据图象找信息
(1)李阿姨每天早晨从家慢跑到小区公园,锻炼一阵后,再慢跑回家.表示李阿姨离开家的距离y (单位:米)与时间t (单位:分)的函数关系的图象大致如上图所示,则李阿姨跑步的路线可能是(用P点表示李阿姨家的位置)( )
A. B. C. D.
(2)均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是( )
A. B. C. D.
(3)一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.则8min时容器内的水量为( )
A.20 L B.25 L C.27L D.30 L
(4)在同一条道路上,甲车从A地到B地,乙车从B地到A地,甲、乙保持匀速运动.乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )
A.乙先出发的时间为0.5小时 B.甲的速度是80千米/小时
C.甲出发0.5小时后两车相遇 D.甲到B地比乙到A地早小时
【答案】(1)A(2)D;(3)B;(4)D;
横扫学霸
例7 如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系.
(1)在这个变化过程中自变量是_____,因变量是_____;
(2)小李何时到达离家最远的地方?此时离家多远?
(3)请直接写出小李何时与家相距20km?
(4)求出小李这次出行的平均速度.
【答案】(1)离家时间,离家距离;(2)2h,30km;(3)t=1.5或t=4;(4)12km/h
例8 如图1,一条笔直的公路上有A、B、C三地,甲、乙两辆汽车分别从A、B两地同时开出,沿公路匀速相向而行,驶往B、A两地.甲、乙两车到C地距离y1、y2(千米)与行驶时间x(时)的部分函数图象如图2所示.
(1)A、B两地距离为_____千米;
(2)M点的坐标是_________;
(3)在图2中补全甲车到C地的距离y1(千米)与行驶时间x(时)的函数图象;
(4)两车行驶多长时间时到C地的距离相等?
【分析】(1)由图象可知AC=60,CB=90,据此来求解;
(2)根据(1)中AB的距离,可求出乙的速度,再由BC的距离,可以求出B到达C的时间;
(3)算出甲车速度,根据AC的距离算出时间,确定终点坐标再画图;
(4)由(3)图可知,两车两次与C点距离相同,一次两车相遇在C点同侧,一次相背而行,在C两侧,从而解出时间.
【答案】(1)150;(2)(1.2,0);(3)甲车速度60km/h,行驶完全程需要2.5h,终点坐标(2.5,90)
(4)由图可知, 在C同侧两车相遇时,150÷(60+75)=
在C异侧,设时间为x,列方程75x-90=60x-60,解得x=2
∴两车行驶或2个小时到C地距离相等.
课后创新培养
课后作业
练1
下列可以表示y为自变量x的函数的是( )
A. B.
C. D.y=1,x∈R
【答案】A
练2
(1) 对于圆的周长公式C=2πR,下列说法错误的是( )
A.π是变量 B.R、C是变量 C.R是自变量 D.C是因变量
(2)函数y=的自变量x的取值范围是( )
A.x≥﹣1 B.x≥﹣1且x≠2 C.x≠±2 D.x>﹣1且x≠2
【答案】(1)A(2)B
练3 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A. B. C. D.
【答案】D
练4 如图,一只蚂蚁从点出发,沿着扇形的边缘匀速爬行一周,设蚂蚁的运动时间为t,蚂蚁到点的距离为S,则关于t的函数图象大致为( )
【答案】C
练5 如图,,分别表示步行与骑车在同一路上行驶的路程与时间的关系.
⑴出发时与相距________千米.
⑵走了一段路后,自行车发生故障,进行修理,所用的时间是________小时.
⑶出发后________小时与相遇.
⑷若的自行车不发生故障,保持出发时的速度前进,________小时与相遇,相遇点离的出发点________千米.
⑸求出行走的路程与时间的函数关系式.(写出过程)
【答案】⑴10;⑵1;⑶3;⑷,;
⑸A行走的路程S与时间t的函数关系式为
先求出速度为(22.5-10)÷3=
路程=10+速度×时间.
8
7
课堂思维碰撞
第一层:变量与函数
知识导入
基本概念
变量与常量
在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
自变量与函数
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一的值与其对应,那么我们就说x是自变量,y是x的函数.如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
解析式
用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数常用的方法.这种式子叫做函数的解析式.
注意:
函数不是数,它是指在一个变化过程中两个变量之间的关系,函数本质就是变量间的对应关系.
⑴对于每一个给定的值,有一个唯一确定的值与之对应,否则就不是的函数.例如就不是函数,因为当时,,即有两个值与对应.
⑵对于每一个给定的值,可以有一个值与之对应,也可以有多个值与之对应.例如在函数中,时,;时,.
确定函数自变量取值范围的方法:
(1)整式型:一般取全体实数
(2)分式型:使得分母不为0
(3)根式型:①根指数为偶数时被开方数为非负数
②根指数为奇数时被开方数为任意实数
(4)非正整数幂:底数不为0
(5)整式、分式和根式的组合型:取各自取值范围的公共部分
(6)实际问题:符合实际意义
夯实基础
例1 基本概念
(1)在圆的周长公式C=2πr中,下列说法错误的是( )
A.C,π,r是变量,2是常量
B.C,r是变量,2π是常量
C.r是自变量,C是r的函数
D.将C=2πr写成,则可看作C是自变量,r是C的函数
(2)某品牌豆浆机成本为70元,销售商对其销量定价的关系进行了调查,结果如下( ):
定价(元) 100 110 120 130 140 150
销量(个) 80 100 110 100 80 60
A.定价是常量,销量是变量
B.定价是变量,销量是不变量
C.定价与销售量都是变量,定价是自变量,销量是因变量
D.定价与销量都是变量,销量是自变量,定价是因变量
【答案】(1)A ;(2)C
能力提升
例2
(1)下列式子中,是的函数的有_____________
①;②;③;④;⑤;⑥y=;⑦
(2)下面每个选项中给出了某个变化过程中的两个变量x和y,其中y不是x的函数的选项是( )
A.y:正方形的面积,x:这个正方形的周长
B.y:某班学生的身高,x:这个班学生的学号
C.y:圆的面积,x:这个圆的直径
D.y:一个正数的平方根,x:这个正数
(3)求下列式子中自变量的取值范围.
① ② ③ ④ ⑤
【答案】(1)①②④⑥⑦;(2)D(3)①全体实数;②x≠3;③x≠-1且x≠0;④;
⑤x≥2且x≠3
例3(1) 等腰周长为,底边长为,腰长为.
①写出关于的函数关系式;
②求的取值范围;
③求的取值范围.
【答案】(1)解:①y=10﹣2x;
②∵x>0,y>0,2x>y∴10﹣2x>0,2x>10﹣2x,解得;
③∵x=5﹣∴<5﹣<5,解得0<y<5.
(2)某地市话的收费标准为:
①通话时间在3分钟以内(包括3分钟)话费每分钟0.2元;
②通话时间超过3分钟时,超过部分的话费按每分钟0.15元计算.
那么话费y(元)与通话时间x(分)之间的关系式为_________(写出自变量的取值范围)
【答案】
第二层: 函数的图象
知识导入
1.函数图象的概念:
对于一个函数,如果把自变量和函数的每对值分别作为点的横坐标与纵坐标,在平面直角坐标系内描出相应的点,这些点所组成的图形,就是函数的图象.
2.函数图象的画法
⑴列表; ⑵描点; ⑶连线.
3.函数解析式与函数图象的关系:
由函数图象的定义可知,图象上任意一点中的,都是解析式方程的一个解.反之,以解析式方程的任意一个解为坐标的点一定在函数的图象上.
判断一个点是否在函数图象上的方法是:将这个点的坐标值代入函数的解析式,如果满足函数解析式,这个点就在函数的图象上,否则就不在这个函数的图象上.
夯实基础
例4 函数图象
如图下列各曲线中表示y是x的函数的是( )
A. B. C. D.
【答案】A
能力提升
例5 根据信息找图象
(1)小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
A. B. C. D.
(2)如图,爸爸从家(点O)出发,沿着等腰三角形AOB的边OA→AB→BO的路径去匀速散步,其中OA=OB.设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )
A. B. C. D.
(3)边长为和的两个正方形,其一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为,大正方形内除去小正方形部分的面积为(阴影部分),则与的大致图象为( )
A B C D
(4)小刚以400米/分的速度匀速骑车5分,在原地休息了6分,然后以500米/分的速度骑回出发地,下列函数图象能表达这一过程的是( )
A. B. C. D.
【答案】(1)D;(2)D;(3)A;(4)C;
例6 根据图象找信息
(1)李阿姨每天早晨从家慢跑到小区公园,锻炼一阵后,再慢跑回家.表示李阿姨离开家的距离y (单位:米)与时间t (单位:分)的函数关系的图象大致如上图所示,则李阿姨跑步的路线可能是(用P点表示李阿姨家的位置)( )
A. B. C. D.
(2)均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是( )
A. B. C. D.
(3)一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.则8min时容器内的水量为( )
A.20 L B.25 L C.27L D.30 L
(4)在同一条道路上,甲车从A地到B地,乙车从B地到A地,甲、乙保持匀速运动.乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )
A.乙先出发的时间为0.5小时 B.甲的速度是80千米/小时
C.甲出发0.5小时后两车相遇 D.甲到B地比乙到A地早小时
【答案】(1)A(2)D;(3)B;(4)D;
横扫学霸
例7 如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系.
(1)在这个变化过程中自变量是_____,因变量是_____;
(2)小李何时到达离家最远的地方?此时离家多远?
(3)请直接写出小李何时与家相距20km?
(4)求出小李这次出行的平均速度.
【答案】(1)离家时间,离家距离;(2)2h,30km;(3)t=1.5或t=4;(4)12km/h
例8 如图1,一条笔直的公路上有A、B、C三地,甲、乙两辆汽车分别从A、B两地同时开出,沿公路匀速相向而行,驶往B、A两地.甲、乙两车到C地距离y1、y2(千米)与行驶时间x(时)的部分函数图象如图2所示.
(1)A、B两地距离为_____千米;
(2)M点的坐标是_________;
(3)在图2中补全甲车到C地的距离y1(千米)与行驶时间x(时)的函数图象;
(4)两车行驶多长时间时到C地的距离相等?
【分析】(1)由图象可知AC=60,CB=90,据此来求解;
(2)根据(1)中AB的距离,可求出乙的速度,再由BC的距离,可以求出B到达C的时间;
(3)算出甲车速度,根据AC的距离算出时间,确定终点坐标再画图;
(4)由(3)图可知,两车两次与C点距离相同,一次两车相遇在C点同侧,一次相背而行,在C两侧,从而解出时间.
【答案】(1)150;(2)(1.2,0);(3)甲车速度60km/h,行驶完全程需要2.5h,终点坐标(2.5,90)
(4)由图可知, 在C同侧两车相遇时,150÷(60+75)=
在C异侧,设时间为x,列方程75x-90=60x-60,解得x=2
∴两车行驶或2个小时到C地距离相等.
课后创新培养
课后作业
练1
下列可以表示y为自变量x的函数的是( )
A. B.
C. D.y=1,x∈R
【答案】A
练2
(1) 对于圆的周长公式C=2πR,下列说法错误的是( )
A.π是变量 B.R、C是变量 C.R是自变量 D.C是因变量
(2)函数y=的自变量x的取值范围是( )
A.x≥﹣1 B.x≥﹣1且x≠2 C.x≠±2 D.x>﹣1且x≠2
【答案】(1)A(2)B
练3 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A. B. C. D.
【答案】D
练4 如图,一只蚂蚁从点出发,沿着扇形的边缘匀速爬行一周,设蚂蚁的运动时间为t,蚂蚁到点的距离为S,则关于t的函数图象大致为( )
【答案】C
练5 如图,,分别表示步行与骑车在同一路上行驶的路程与时间的关系.
⑴出发时与相距________千米.
⑵走了一段路后,自行车发生故障,进行修理,所用的时间是________小时.
⑶出发后________小时与相遇.
⑷若的自行车不发生故障,保持出发时的速度前进,________小时与相遇,相遇点离的出发点________千米.
⑸求出行走的路程与时间的函数关系式.(写出过程)
【答案】⑴10;⑵1;⑶3;⑷,;
⑸A行走的路程S与时间t的函数关系式为
先求出速度为(22.5-10)÷3=
路程=10+速度×时间.
8
7
