2021—2022学年苏科版数学七年级下册9.4乘法公式—完全平方公式课件(共27张ppt)
文档属性
| 名称 | 2021—2022学年苏科版数学七年级下册9.4乘法公式—完全平方公式课件(共27张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 549.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 12:29:00 | ||
图片预览






文档简介
(共27张PPT)
三角形的内角和(1)
9.4 乘法公式(1)
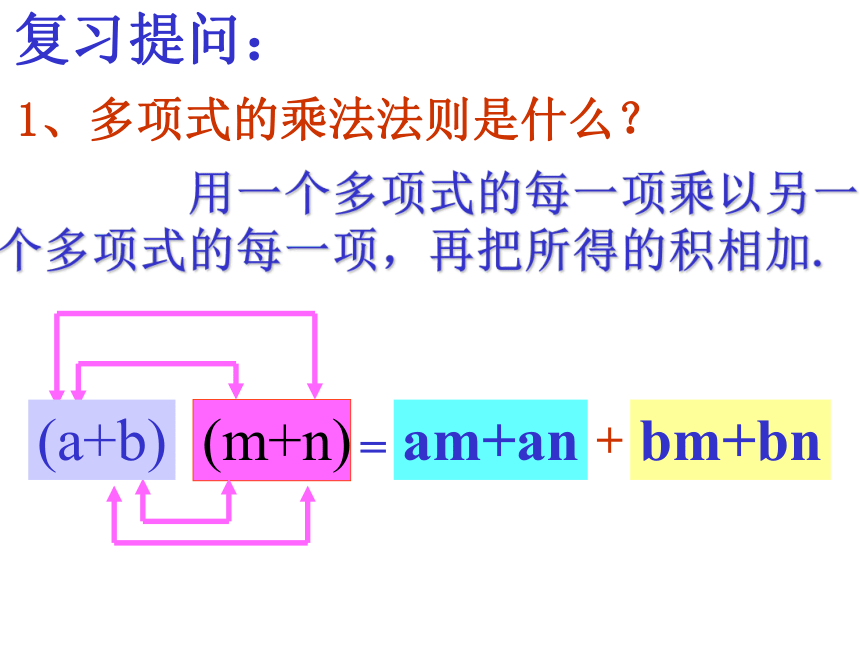
复习提问:
用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
1、多项式的乘法法则是什么?
am+an
bm+bn
+
=
(m+n)
(a+b)
算一算
3、(a+b)2
4、(a-b)2
1、(a+1)(a+1)
2、(mn+a)(mn+a)
算一算:
3、(a+b)2
4、(a-b)2
= a2 +2ab+b2
= a2 - 2ab+b2
= a2 +ab +ab +b2
= a2 - ab - ab +b2
=(a+b) (a+b)
=(a-b) (a-b)
§9.4完全平方公式(一)
完全平方公式的数学表达式:
完全平方公式的文字叙述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
(a+b)2= a2 +b2 +2ab
(a-b)2= a2 +b2 - 2ab
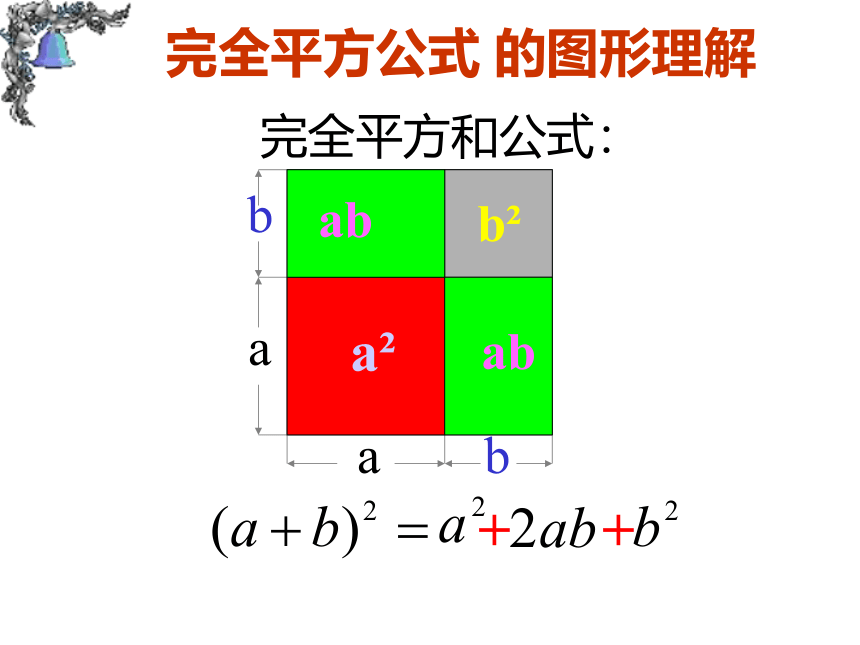
(a+b)2= a2 +2ab+b2
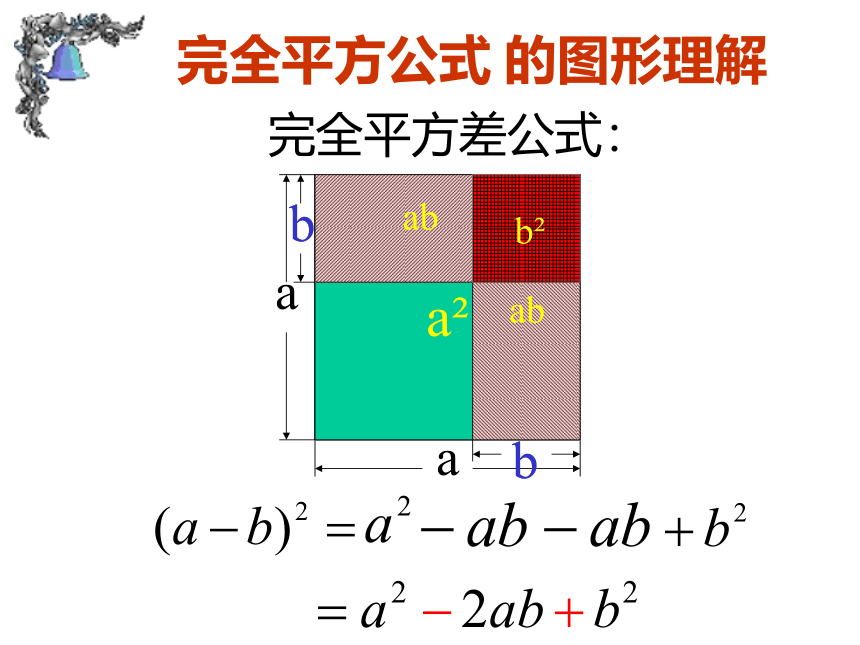
(a-b)2= a2 - 2ab+b2
b
b
a
a
(a+b)
a
b
ab
ab
+
+
完全平方和公式:
完全平方公式 的图形理解
a
a
b
b
(a-b)
a
ab
ab
b
b
b
完全平方差公式:
完全平方公式 的图形理解
公式特点:
4、公式中的字母a,b可以表示数,单项式和
多项式。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中
间的符号相同。
首平方,尾平方,首尾两倍中间放
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (x -y)2 =x2+2xy +y2
(4) (x+y)2 =x2 +xy +y2
错
错
错
错
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(x -y)2 =x2 -2xy +y2
(x +y)2 =x2+2xy +y2
例1 运用完全平方公式计算:
解: (x+2y)2=
=x2
(1)(x+2y)2
(a +b)2= a2 + 2 ab + b2
x2
+2 x 2y
+(2y)2
+4xy
+4y2
例1 运用完全平方公式计算:
解: (x-2y)2=
=x2
(2)(x-2y)2
(a - b)2= a2 - 2 ab + b2
x2
-2 x 2y
+(2y)2
-4xy
+4y2
(1)(2x+y)2 =
(2)(4-y)2 =
(3)(2m-n)2=
算一算
例2、运用完全平方公式计算:
(1) ( 4m2 - n2 )2
分析:
4m2
a
n2
b
解:
( 4m2 - n2)2
=( )2-2( )·( )+( )2
=16m4-8m2n2+n4
记清公式、代准数式、准确计算。
解题过程分3步:
(a-b)2= a2 - 2ab+b2
4m2
4m2
n2
n2
1.(3x2-7y)2=
2.(2a2+3b3)2=
算一算
在解题过程中要准确确定a和b、对照公式原形的两边, 做到
(1)不丢项
(2)不弄错符号
(3)2ab时不少乘2;
(4)两数是乘积形式时,被平方时要注意添括号
填空
(1)(a+ )2=a2+4ab+4b2
(2) (2a+ )2=4a2+4ab+b2
(3) (3x- )2=9x2-12xy2+( )
(4)( -x- )2=x2+ +1
议一议
如何计算 (a+b+c)2
解: (a+b+c)2
=[(a+b)+c]2
=(a+b)2+2·(a+b)·c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc
例3、运用完全平方公式进行简便计算:
(1) 1042
解: 1042
= (100+4)2
=10000+800+16
=10816
(2) 99.92
解: 99.92
= (100 –0. 1)2
=10000 -20+0.01
=9998.01
1992=
8.92=
练习:利用完全平方公式计算:
1012=
例4 计算:
(-a+b)2 =(b-a)2 =(a-b)2
解:原式=
(-a-b)2 =(a+b)2
解:原式=
1.(-x-y)2=
2.(-2a2+b)2=
你会了吗
小兵计算一个二项整式的平方式时得到
正确结果是4x2+ +25y2,但中间一项
不慎被污染了,这一项应是( )
A 10xy B 20xy C±10xy D±20xy
(1) (6a+5b)2
=36a2+60ab+25b2
(2) (4x-3y)2
=16x2-24xy+9y2
(4) (2m-1)2
=4m2-4m+1
(3) (-2m-1)2
=4m2+4m+1
课堂检测
(1)(6a+5b)2 (3)(-2m-1)2
(2)(4x-3y)2 (4)(2m-1)2
解:
本节课你的收获是什么?
小结
本节课你学到了什么
有时需要进行变形,使变形后的式子符合应用
完全平方公式的条件,即为“两数和(或差)的
平方”,然后应用公式计算.
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;第一(二)数是乘积被平方时要注意添括号, 是运用完全平方公式进行多项式乘法的关键
已知a+b=2,ab=1.
求a2+b2、(a-b)2的值.
挑战自我
三角形的内角和(1)
9.4 乘法公式(1)
复习提问:
用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
1、多项式的乘法法则是什么?
am+an
bm+bn
+
=
(m+n)
(a+b)
算一算
3、(a+b)2
4、(a-b)2
1、(a+1)(a+1)
2、(mn+a)(mn+a)
算一算:
3、(a+b)2
4、(a-b)2
= a2 +2ab+b2
= a2 - 2ab+b2
= a2 +ab +ab +b2
= a2 - ab - ab +b2
=(a+b) (a+b)
=(a-b) (a-b)
§9.4完全平方公式(一)
完全平方公式的数学表达式:
完全平方公式的文字叙述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
(a+b)2= a2 +b2 +2ab
(a-b)2= a2 +b2 - 2ab
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
b
b
a
a
(a+b)
a
b
ab
ab
+
+
完全平方和公式:
完全平方公式 的图形理解
a
a
b
b
(a-b)
a
ab
ab
b
b
b
完全平方差公式:
完全平方公式 的图形理解
公式特点:
4、公式中的字母a,b可以表示数,单项式和
多项式。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中
间的符号相同。
首平方,尾平方,首尾两倍中间放
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (x -y)2 =x2+2xy +y2
(4) (x+y)2 =x2 +xy +y2
错
错
错
错
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(x -y)2 =x2 -2xy +y2
(x +y)2 =x2+2xy +y2
例1 运用完全平方公式计算:
解: (x+2y)2=
=x2
(1)(x+2y)2
(a +b)2= a2 + 2 ab + b2
x2
+2 x 2y
+(2y)2
+4xy
+4y2
例1 运用完全平方公式计算:
解: (x-2y)2=
=x2
(2)(x-2y)2
(a - b)2= a2 - 2 ab + b2
x2
-2 x 2y
+(2y)2
-4xy
+4y2
(1)(2x+y)2 =
(2)(4-y)2 =
(3)(2m-n)2=
算一算
例2、运用完全平方公式计算:
(1) ( 4m2 - n2 )2
分析:
4m2
a
n2
b
解:
( 4m2 - n2)2
=( )2-2( )·( )+( )2
=16m4-8m2n2+n4
记清公式、代准数式、准确计算。
解题过程分3步:
(a-b)2= a2 - 2ab+b2
4m2
4m2
n2
n2
1.(3x2-7y)2=
2.(2a2+3b3)2=
算一算
在解题过程中要准确确定a和b、对照公式原形的两边, 做到
(1)不丢项
(2)不弄错符号
(3)2ab时不少乘2;
(4)两数是乘积形式时,被平方时要注意添括号
填空
(1)(a+ )2=a2+4ab+4b2
(2) (2a+ )2=4a2+4ab+b2
(3) (3x- )2=9x2-12xy2+( )
(4)( -x- )2=x2+ +1
议一议
如何计算 (a+b+c)2
解: (a+b+c)2
=[(a+b)+c]2
=(a+b)2+2·(a+b)·c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc
例3、运用完全平方公式进行简便计算:
(1) 1042
解: 1042
= (100+4)2
=10000+800+16
=10816
(2) 99.92
解: 99.92
= (100 –0. 1)2
=10000 -20+0.01
=9998.01
1992=
8.92=
练习:利用完全平方公式计算:
1012=
例4 计算:
(-a+b)2 =(b-a)2 =(a-b)2
解:原式=
(-a-b)2 =(a+b)2
解:原式=
1.(-x-y)2=
2.(-2a2+b)2=
你会了吗
小兵计算一个二项整式的平方式时得到
正确结果是4x2+ +25y2,但中间一项
不慎被污染了,这一项应是( )
A 10xy B 20xy C±10xy D±20xy
(1) (6a+5b)2
=36a2+60ab+25b2
(2) (4x-3y)2
=16x2-24xy+9y2
(4) (2m-1)2
=4m2-4m+1
(3) (-2m-1)2
=4m2+4m+1
课堂检测
(1)(6a+5b)2 (3)(-2m-1)2
(2)(4x-3y)2 (4)(2m-1)2
解:
本节课你的收获是什么?
小结
本节课你学到了什么
有时需要进行变形,使变形后的式子符合应用
完全平方公式的条件,即为“两数和(或差)的
平方”,然后应用公式计算.
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;第一(二)数是乘积被平方时要注意添括号, 是运用完全平方公式进行多项式乘法的关键
已知a+b=2,ab=1.
求a2+b2、(a-b)2的值.
挑战自我
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
