八年级上册第十一章 三角形第5讲三角形的认识(教案)
文档属性
| 名称 | 八年级上册第十一章 三角形第5讲三角形的认识(教案) |  | |
| 格式 | zip | ||
| 文件大小 | 473.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 10:58:15 | ||
图片预览



文档简介
第5讲 三角形的认识
课堂修炼塔
第一层:三角形的基本概念
技能天赋:
知识点 典型范例
三角形的定义: 由不在同一直线上的三条线段首尾顺次相接所组成的平面图形叫做三角形. 表示法及读法: 三角形用符号“”表示,顶点是、、的三角形记作“”,读作“三角形”.
三角形的性质:三角形具有稳定性.
三角形的内角: 三角形的每两条边所组成的角叫做三角形的内角,简称三角形的角. 三角形内角和定理: 三角形三个内角的和等于180°. ∠A,∠B,∠C是△ABC的内角.
三角形的边: 组成三角形的三条线段叫做三角形的边. 的三边可以用AB、AC、BC表示,也可以用、、表示. 顶点A的对边a(BC) 顶点B的对边b(AC) 顶点C的对边c(AB)
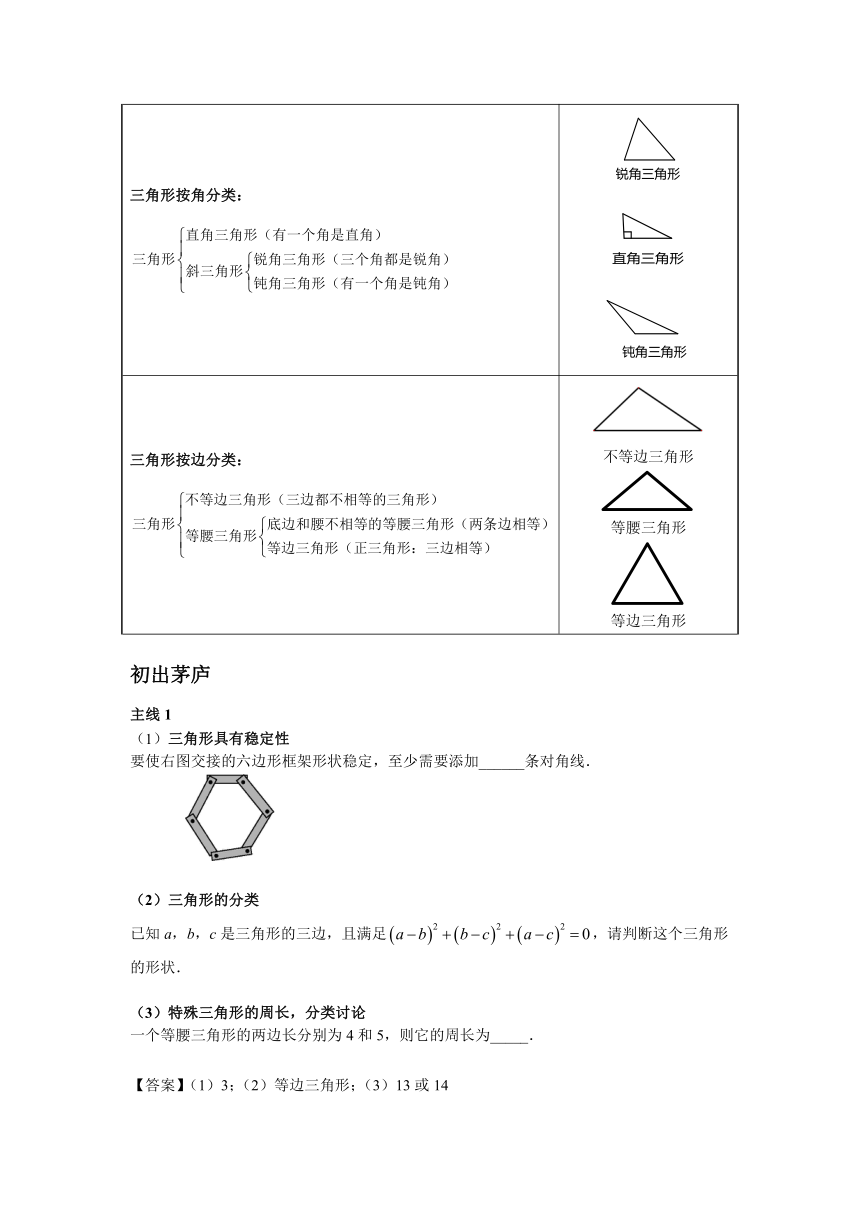
三角形按角分类:
三角形按边分类: 不等边三角形 等腰三角形 等边三角形
初出茅庐
主线1
(1)三角形具有稳定性
要使右图交接的六边形框架形状稳定,至少需要添加______条对角线.
(2)三角形的分类
已知a,b,c是三角形的三边,且满足,请判断这个三角形的形状.
(3)特殊三角形的周长,分类讨论
一个等腰三角形的两边长分别为4和5,则它的周长为_____.
【答案】(1)3;(2)等边三角形;(3)13或14
第二层:三角形的边
技能天赋
知识点 典型范例
三角形的三边关系: 三边关系定理:三角形任意两边之和大于第三边; 三边关系定理的推论:三角形任意两边之差小于第三边. 即:a,b,c三条线段可组成三角形 两条较小的线段之和大于最大的线段 技巧:在应用三边关系定理及推论时,可以简化为: (1)当三条线段中最长的线段小于另两条线段之和时; (2)当三条线段中最短的线段大于另两条线段之差时; 即可组成三角形 其中, a+c>b,|a-c|<b a+b>c,|a-b|<c b+c>a,|b-c|<a
初出茅庐
主线2 三边关系
(1)下面四组数都表示线段的长度,①;②;③三条线段a,b,c,满足,,;④.(以上字母都是正数)
以每组线段为边能够组成三角形的是( )
A.①② B.②③ C.①③④ D.①④
(2)小明有两根、的木棒,他想以这两根木棒为边做一个等腰三角形,还需再选用一根( )长的木棒.
A. B.
C.或 D.大于且小于的任意长
(3)设是的三边长,则:__
【答案】(1)A;(2)B;(3)
主线3 三边关系进阶
(1)若三角形的两边长分别为和,则第三边的长可能是( )
A. B. C. D.
(2)如图,四边形中,,,,,则的取值范围是
(3)已知的边长分别为,,5,则的周长的取值范围是( )
A. B. C. D.
(4)已知有两边长为、,其中,则其周长一定满足( ).
A. B. C. D.
【答案】(1)C;(2);(3)D;(4)A
终极试炼
主线4 整数边三角形
(1)已知三角形的三边长a、b、c都是整数,且,如果,则有__个满足题意的三角形;
(2)已知三角形的三边长a、b、c都是整数,且,如果,则有__个满足题意的三角形;
【答案】(1)15;(2)28
第三层:三角形的重要线段
技能天赋
知识点 典型范例
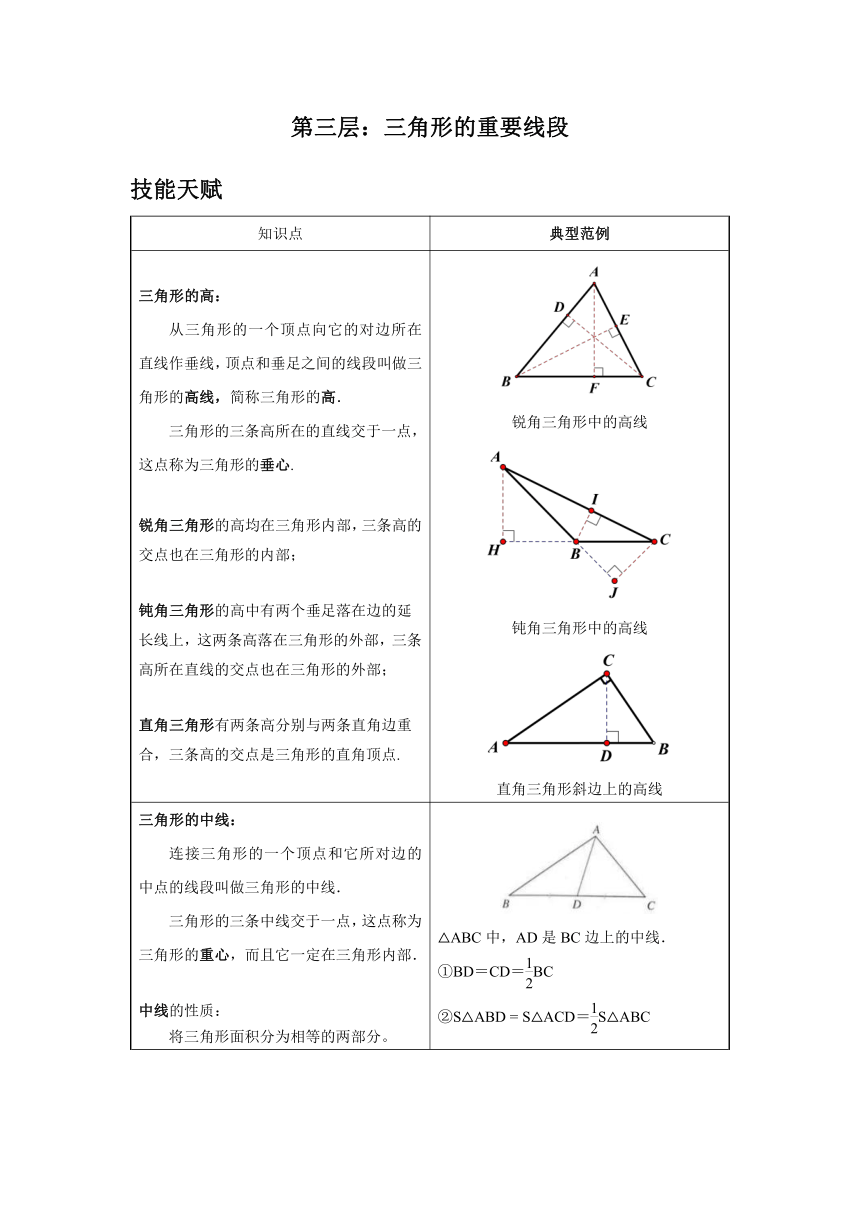
三角形的高: 从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高. 三角形的三条高所在的直线交于一点,这点称为三角形的垂心. 锐角三角形的高均在三角形内部,三条高的交点也在三角形的内部; 钝角三角形的高中有两个垂足落在边的延长线上,这两条高落在三角形的外部,三条高所在直线的交点也在三角形的外部; 直角三角形有两条高分别与两条直角边重合,三条高的交点是三角形的直角顶点. 锐角三角形中的高线 钝角三角形中的高线 直角三角形斜边上的高线
三角形的中线: 连接三角形的一个顶点和它所对边的中点的线段叫做三角形的中线. 三角形的三条中线交于一点,这点称为三角形的重心,而且它一定在三角形内部. 中线的性质: 将三角形面积分为相等的两部分。 △ABC中,AD是BC边上的中线. ①BD=CD=BC ②S△ABD = S△ACD=S△ABC
三角形的角平分线: 三角形的一个内角的角平分线与它的对边相交,连接这个角的顶点和交点的线段叫做三角形的角平分线. 注:角的平分线是一条射线,三角形的角平分线是一条线段. △ABC中,AD是的角平分线. ∠BAD=∠CAD=∠BAC
能力觉醒
主线5 三角形的中线、高与面积综合
(1)如图,在△ABC中,D,E分别是BC、AD的中点,且S△ACE=2,则S△ABC=___;
(2)如图,为的中线,为的中线.若的面积为,,则点到边的距离为______
(3)如图,在中,点分别为边的中点,且,则=__________
(4)如图,在中,点、、分别在三条边上,点为中点,、、交于一点,,,,则的面积是( )
A. B. C. D.
【答案】(1)8;(2)4;(3);(4)B
主线6 三角形的角平分线、高与角度综合
如图所示,△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=30°,∠C=70°,求∠DAE的度数;
(2)△ABC中,若∠B=α,∠C=β(α<β),请你根据(1)问的结果大胆猜想∠DAE与α,β间的等量关系,并说明理由.
【答案】
(1)∵∠B=30°,∠C=70°,∴∠BAC=180°-30°-70°=80°.
∵AE平分∠BAC,∴∠BAE=∠CAE=80°÷2=40°.
∵AD⊥BC,∴∠ADE=90°.
∵∠AED=∠B+∠BAE=30°+40°=70°,∴∠DAE=90°-70°=20°.
(2)根据(1)问的结果,猜想∠DAE与α,β间的等量关系为:∠DAE=,
∵∠B=α,∠C=β,∴∠BAC=180°﹣α﹣β,
∵AE平分∠BAC,∴∠BAE=∠CAE=(180°﹣α﹣β)÷2=90°﹣,
∵∠AED=∠B+∠BAE=α+(90°﹣)=90°+,
∴∠DAE=90°﹣(90°+)=.
终极试炼
主线7重心性质的证明
如图,已知:在△ABC中,D、E、F分别是BC、AC、AB的中点.求证:OB=2OE.
【答案】有三角形的中线性质可知:
,,
,,
即有:,
∴
∵△AOB与△AOE的高相同,则它们的底边之比等于面积之比,
∴OB=2OE
主线8 三边关系与高的综合
不等边三角形中,如果一条边长等于另两条边长的平均值,那么,最大边上的高与最小边上的高的比值的取值范围是 .
【答案】
课后竞技场
日常任务
任务1 已知四根长度分别为,,, 的木棒,任意选取三根木棒组成一个三角形,那么可以组成三角形的个数为( )
A.个 B.个 C.个 D.个
【答案】C
任务2 如果三角形的两边长分别为和,第三边长是偶数,则第三边长可以是( )
A. B. C. D.
【答案】C
任务3 如图所示,是的中线,已知,,则与的周长差是_________.
【答案】cm
任务4 如图,是的中线,是的中点,是的中点,的面积为,则的面积是_________.
【答案】
任务5 如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°.求∠DAC和∠BOA的度数.
【答案】∠DAC=20°,∠BOA=125°
课堂修炼塔
第一层:三角形的基本概念
技能天赋:
知识点 典型范例
三角形的定义: 由不在同一直线上的三条线段首尾顺次相接所组成的平面图形叫做三角形. 表示法及读法: 三角形用符号“”表示,顶点是、、的三角形记作“”,读作“三角形”.
三角形的性质:三角形具有稳定性.
三角形的内角: 三角形的每两条边所组成的角叫做三角形的内角,简称三角形的角. 三角形内角和定理: 三角形三个内角的和等于180°. ∠A,∠B,∠C是△ABC的内角.
三角形的边: 组成三角形的三条线段叫做三角形的边. 的三边可以用AB、AC、BC表示,也可以用、、表示. 顶点A的对边a(BC) 顶点B的对边b(AC) 顶点C的对边c(AB)
三角形按角分类:
三角形按边分类: 不等边三角形 等腰三角形 等边三角形
初出茅庐
主线1
(1)三角形具有稳定性
要使右图交接的六边形框架形状稳定,至少需要添加______条对角线.
(2)三角形的分类
已知a,b,c是三角形的三边,且满足,请判断这个三角形的形状.
(3)特殊三角形的周长,分类讨论
一个等腰三角形的两边长分别为4和5,则它的周长为_____.
【答案】(1)3;(2)等边三角形;(3)13或14
第二层:三角形的边
技能天赋
知识点 典型范例
三角形的三边关系: 三边关系定理:三角形任意两边之和大于第三边; 三边关系定理的推论:三角形任意两边之差小于第三边. 即:a,b,c三条线段可组成三角形 两条较小的线段之和大于最大的线段 技巧:在应用三边关系定理及推论时,可以简化为: (1)当三条线段中最长的线段小于另两条线段之和时; (2)当三条线段中最短的线段大于另两条线段之差时; 即可组成三角形 其中, a+c>b,|a-c|<b a+b>c,|a-b|<c b+c>a,|b-c|<a
初出茅庐
主线2 三边关系
(1)下面四组数都表示线段的长度,①;②;③三条线段a,b,c,满足,,;④.(以上字母都是正数)
以每组线段为边能够组成三角形的是( )
A.①② B.②③ C.①③④ D.①④
(2)小明有两根、的木棒,他想以这两根木棒为边做一个等腰三角形,还需再选用一根( )长的木棒.
A. B.
C.或 D.大于且小于的任意长
(3)设是的三边长,则:__
【答案】(1)A;(2)B;(3)
主线3 三边关系进阶
(1)若三角形的两边长分别为和,则第三边的长可能是( )
A. B. C. D.
(2)如图,四边形中,,,,,则的取值范围是
(3)已知的边长分别为,,5,则的周长的取值范围是( )
A. B. C. D.
(4)已知有两边长为、,其中,则其周长一定满足( ).
A. B. C. D.
【答案】(1)C;(2);(3)D;(4)A
终极试炼
主线4 整数边三角形
(1)已知三角形的三边长a、b、c都是整数,且,如果,则有__个满足题意的三角形;
(2)已知三角形的三边长a、b、c都是整数,且,如果,则有__个满足题意的三角形;
【答案】(1)15;(2)28
第三层:三角形的重要线段
技能天赋
知识点 典型范例
三角形的高: 从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高. 三角形的三条高所在的直线交于一点,这点称为三角形的垂心. 锐角三角形的高均在三角形内部,三条高的交点也在三角形的内部; 钝角三角形的高中有两个垂足落在边的延长线上,这两条高落在三角形的外部,三条高所在直线的交点也在三角形的外部; 直角三角形有两条高分别与两条直角边重合,三条高的交点是三角形的直角顶点. 锐角三角形中的高线 钝角三角形中的高线 直角三角形斜边上的高线
三角形的中线: 连接三角形的一个顶点和它所对边的中点的线段叫做三角形的中线. 三角形的三条中线交于一点,这点称为三角形的重心,而且它一定在三角形内部. 中线的性质: 将三角形面积分为相等的两部分。 △ABC中,AD是BC边上的中线. ①BD=CD=BC ②S△ABD = S△ACD=S△ABC
三角形的角平分线: 三角形的一个内角的角平分线与它的对边相交,连接这个角的顶点和交点的线段叫做三角形的角平分线. 注:角的平分线是一条射线,三角形的角平分线是一条线段. △ABC中,AD是的角平分线. ∠BAD=∠CAD=∠BAC
能力觉醒
主线5 三角形的中线、高与面积综合
(1)如图,在△ABC中,D,E分别是BC、AD的中点,且S△ACE=2,则S△ABC=___;
(2)如图,为的中线,为的中线.若的面积为,,则点到边的距离为______
(3)如图,在中,点分别为边的中点,且,则=__________
(4)如图,在中,点、、分别在三条边上,点为中点,、、交于一点,,,,则的面积是( )
A. B. C. D.
【答案】(1)8;(2)4;(3);(4)B
主线6 三角形的角平分线、高与角度综合
如图所示,△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=30°,∠C=70°,求∠DAE的度数;
(2)△ABC中,若∠B=α,∠C=β(α<β),请你根据(1)问的结果大胆猜想∠DAE与α,β间的等量关系,并说明理由.
【答案】
(1)∵∠B=30°,∠C=70°,∴∠BAC=180°-30°-70°=80°.
∵AE平分∠BAC,∴∠BAE=∠CAE=80°÷2=40°.
∵AD⊥BC,∴∠ADE=90°.
∵∠AED=∠B+∠BAE=30°+40°=70°,∴∠DAE=90°-70°=20°.
(2)根据(1)问的结果,猜想∠DAE与α,β间的等量关系为:∠DAE=,
∵∠B=α,∠C=β,∴∠BAC=180°﹣α﹣β,
∵AE平分∠BAC,∴∠BAE=∠CAE=(180°﹣α﹣β)÷2=90°﹣,
∵∠AED=∠B+∠BAE=α+(90°﹣)=90°+,
∴∠DAE=90°﹣(90°+)=.
终极试炼
主线7重心性质的证明
如图,已知:在△ABC中,D、E、F分别是BC、AC、AB的中点.求证:OB=2OE.
【答案】有三角形的中线性质可知:
,,
,,
即有:,
∴
∵△AOB与△AOE的高相同,则它们的底边之比等于面积之比,
∴OB=2OE
主线8 三边关系与高的综合
不等边三角形中,如果一条边长等于另两条边长的平均值,那么,最大边上的高与最小边上的高的比值的取值范围是 .
【答案】
课后竞技场
日常任务
任务1 已知四根长度分别为,,, 的木棒,任意选取三根木棒组成一个三角形,那么可以组成三角形的个数为( )
A.个 B.个 C.个 D.个
【答案】C
任务2 如果三角形的两边长分别为和,第三边长是偶数,则第三边长可以是( )
A. B. C. D.
【答案】C
任务3 如图所示,是的中线,已知,,则与的周长差是_________.
【答案】cm
任务4 如图,是的中线,是的中点,是的中点,的面积为,则的面积是_________.
【答案】
任务5 如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°.求∠DAC和∠BOA的度数.
【答案】∠DAC=20°,∠BOA=125°
