八年级上册第十一章 三角形11.2 与三角形有关的角第6讲三角形的角(教案)
文档属性
| 名称 | 八年级上册第十一章 三角形11.2 与三角形有关的角第6讲三角形的角(教案) |  | |
| 格式 | zip | ||
| 文件大小 | 362.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 11:01:30 | ||
图片预览




文档简介
第6话:三角形的角
课堂修炼塔
第一层:三角形的内角
技能天赋
知识点 典型范例
三角形的内角: 三角形的每两条边所组成的角叫做三角形的内角,简称三角形的角. ∠A,∠B,∠C是△ABC的内角.
三角形内角和定理: 三角形三个内角的和等于180° 在△ABC中,
三角形内角和定理的推论: ①直角三角形两锐角互余; ②有两个角互余的三角形是直角三角形. Rt△ABC中,∠A+∠B=90°
初出茅庐
主线1 内角和定理
(1)中,,则的度数为_______
(2)如图,在锐角中,,分别是,边上的高且交于O点,若,则的度数是( )
A. B. C. D.
(3)一个正方形和两个等边三角形的位置如图所示,若,则( )
A. B. C. D.
【答案】(1);(2)B;(3)B
主线2 内角和定理综合进阶
(1)在中,,且,则是( )
A.锐角三角形 B.钝角三角形
C.有一个角是的直角三角形 D.等腰直角三角形
(2)中,,是边上的高,,则______度.
【答案】(1)B;(2);(3)
能力觉醒
主线3
(1)已知三角形的三个内角分别为、、,且,,则的取值范围是
(2)在中,三个内角的度数均为整数,且,,则的度数为
【答案】(1);(2)
第二层:三角形的外角
技能天赋
知识点 典型范例
三角形的外角: 三角形的任意一边与另一边的延长线所组成的角叫做三角形的外角. 如图,∠BAD,∠ACF,∠CBE是的外角.
三角形的外角性质: ①三角形的外角等于不相邻的两个内角之和; ②三角形的外角大于任何一个不相邻的内角. 如:外角 , , ,
三角形的外角和: 每个顶点处取一个外角再相加,叫三角形的外角和. 三角形的外角和等于. 注:三角形的外角与相邻的内角互为邻补角,因为每个内角均有两个邻补角,因此三角形共有六个外角,其中有三个与另外三个相等.每个顶点处的两个外角是相等的. ∠1+∠2+∠3=360°
初出茅庐
主线4 外角的性质及内外角综合
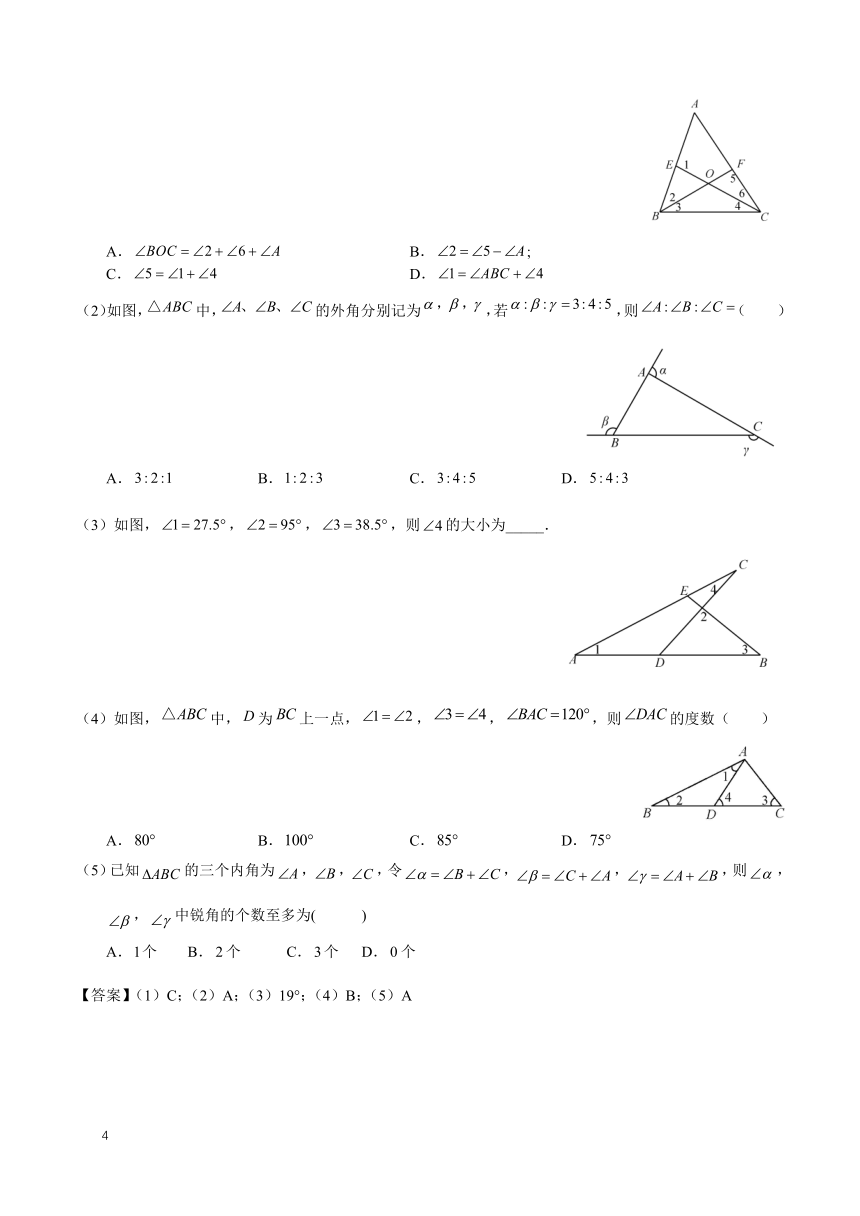
(1)如图所示,在中,,分别在,上,则下列各式不能成立的是( )
A. B.;
C. D.
(2)如图,中,的外角分别记为,若,则( )
A. B. C. D.
(3)如图,,,,则的大小为_____.
(4)如图,中,为上一点,,,,则的度数( )
A. B. C. D.
(5)已知的三个内角为,,,令,,,则,,中锐角的个数至多为( )
A.个 B.个 C.个 D.个
【答案】(1)C;(2)A;(3)19°;(4)B;(5)A
能力觉醒
主线5 角度计算
如图所示,则的度数为_ _
【答案】180°
主线6 如图,,为的两个外角,射线、分别平分、,交的延长线交于点,,,求的度数.
【答案】
∴
∴,∴
第三层:多边形及其内角和
技能天赋
1、基本概念
知识点 典型范例
多边形的定义: 在平面内,由一些线段首尾顺次相接组成的图形叫做多边形. 三角形是最简单的多边形. (以正五边形为例) 多边形ABCDE的边为________, 多边形ABCDE的顶点是__________, 多边形ABCDE的内角是______ _, 多边形ABCDE的外角是_________, 多边形ABCDE的对角线是________.
多边形的分类: 凸多边形: 如果多边形的任何一边所在直线都使余下的边都在这条直线的同一侧,那么这个多边形叫做凸多边形. 凹多边形: 如果多边形中的有一边所在直线使余下的边不都在这条直线的同一侧,那么这个多边形叫做凹多边形. 凸多边形 凹多边形
正多边形: 各个角相等,且各条边都相等的多边形叫做正多边形. 正三边形 正四边形 正五边形 正六边形
2、多边形中的规律
知识点 典型范例
多边形的内角和定理: 边形的内角和为
多边形的外角和定理: 多边形的外角和都是
n边形的对角线: 一个顶点有条对角线,共有条对角线 以六边形为例,每个顶点有6条对角线.
注意:不特别强调多边形都指凸多边形,凸多边形的每个内角都小于.
初出茅庐
主线7 多边形的规律
(1)如右图,小明从点出发,向前走米,左拐,再向前走米,再左拐,如此下去,小明能否回到出发点?如果能,第一次回到出发点共走了多少路程?
(2)m边形的一个顶点有7条对角线,n边形没有对角线,k边形对角线条数等于边数,则 .
(3)幼儿园的小朋友们打算选择一种形状、大小都相同的多边形塑胶板铺活动室的地面,为了保证铺地时既无缝隙又不重叠,请你告诉他们下面形状的塑胶板可以选择的是( ).
①三角形;②四边形;③正五边形;④正六边形;⑤正八边形.
A.③④⑤
B.①②④
C.①④
D.①③④⑤
【答案】(1)能,;(2)18;(3)B
能力觉醒
主线8 多边形的应用
(1)一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为_______
(2)如图,已知,则是______度
(3)能否同时用正三角形和正四边形镶嵌?如果可以,请写出具体的镶嵌方法.
【答案】(1)5或6或7;(2)140°;(3)3个正三角形加上2个正四边形.
终极试炼
主线9 角度计算
如图,,则n = ____
【答案】n=6.
法一:连接BF,
等于五角星ABDFG的内角和加上四边形BCEF的内角和,
五角星ABDFG的内角和为180°,四边形BCEF的内角和为360°,
故,∴n=6
法二:连接BE、GE,设AF与DG相交于点H,与BG相交于点M,与EG相交于点N
由外角性质的:
在△ADH中,,
在△MNG中,,
在△EFN中,
∴= △BCE的三个内角 + 四边形BMNE的四个内角=540°
∴n=6
课后竞技场
日常任务
任务1具备下列条件的三角形中,不是直角三角形的是( )
A. B.
C. D.,
【答案】D
任务2 如图,在中,,若沿图中虚线剪去,则等于( )
A. B. C. D.
【答案】B
任务3 如图所示,若,,,则等于( )
A.120° B.115° C.110° D.105°
【答案】B
任务4
(1)一个正多边形的外角与它相邻的内角之比为1:4,那么这个多边形的边数为( ).
A.8 B.9 C.10 D.12
【答案】C
(2)已知一个多边形的对角线的条数为边数的倍,求该多边形的边数.
【答案】
6
7
课堂修炼塔
第一层:三角形的内角
技能天赋
知识点 典型范例
三角形的内角: 三角形的每两条边所组成的角叫做三角形的内角,简称三角形的角. ∠A,∠B,∠C是△ABC的内角.
三角形内角和定理: 三角形三个内角的和等于180° 在△ABC中,
三角形内角和定理的推论: ①直角三角形两锐角互余; ②有两个角互余的三角形是直角三角形. Rt△ABC中,∠A+∠B=90°
初出茅庐
主线1 内角和定理
(1)中,,则的度数为_______
(2)如图,在锐角中,,分别是,边上的高且交于O点,若,则的度数是( )
A. B. C. D.
(3)一个正方形和两个等边三角形的位置如图所示,若,则( )
A. B. C. D.
【答案】(1);(2)B;(3)B
主线2 内角和定理综合进阶
(1)在中,,且,则是( )
A.锐角三角形 B.钝角三角形
C.有一个角是的直角三角形 D.等腰直角三角形
(2)中,,是边上的高,,则______度.
【答案】(1)B;(2);(3)
能力觉醒
主线3
(1)已知三角形的三个内角分别为、、,且,,则的取值范围是
(2)在中,三个内角的度数均为整数,且,,则的度数为
【答案】(1);(2)
第二层:三角形的外角
技能天赋
知识点 典型范例
三角形的外角: 三角形的任意一边与另一边的延长线所组成的角叫做三角形的外角. 如图,∠BAD,∠ACF,∠CBE是的外角.
三角形的外角性质: ①三角形的外角等于不相邻的两个内角之和; ②三角形的外角大于任何一个不相邻的内角. 如:外角 , , ,
三角形的外角和: 每个顶点处取一个外角再相加,叫三角形的外角和. 三角形的外角和等于. 注:三角形的外角与相邻的内角互为邻补角,因为每个内角均有两个邻补角,因此三角形共有六个外角,其中有三个与另外三个相等.每个顶点处的两个外角是相等的. ∠1+∠2+∠3=360°
初出茅庐
主线4 外角的性质及内外角综合
(1)如图所示,在中,,分别在,上,则下列各式不能成立的是( )
A. B.;
C. D.
(2)如图,中,的外角分别记为,若,则( )
A. B. C. D.
(3)如图,,,,则的大小为_____.
(4)如图,中,为上一点,,,,则的度数( )
A. B. C. D.
(5)已知的三个内角为,,,令,,,则,,中锐角的个数至多为( )
A.个 B.个 C.个 D.个
【答案】(1)C;(2)A;(3)19°;(4)B;(5)A
能力觉醒
主线5 角度计算
如图所示,则的度数为_ _
【答案】180°
主线6 如图,,为的两个外角,射线、分别平分、,交的延长线交于点,,,求的度数.
【答案】
∴
∴,∴
第三层:多边形及其内角和
技能天赋
1、基本概念
知识点 典型范例
多边形的定义: 在平面内,由一些线段首尾顺次相接组成的图形叫做多边形. 三角形是最简单的多边形. (以正五边形为例) 多边形ABCDE的边为________, 多边形ABCDE的顶点是__________, 多边形ABCDE的内角是______ _, 多边形ABCDE的外角是_________, 多边形ABCDE的对角线是________.
多边形的分类: 凸多边形: 如果多边形的任何一边所在直线都使余下的边都在这条直线的同一侧,那么这个多边形叫做凸多边形. 凹多边形: 如果多边形中的有一边所在直线使余下的边不都在这条直线的同一侧,那么这个多边形叫做凹多边形. 凸多边形 凹多边形
正多边形: 各个角相等,且各条边都相等的多边形叫做正多边形. 正三边形 正四边形 正五边形 正六边形
2、多边形中的规律
知识点 典型范例
多边形的内角和定理: 边形的内角和为
多边形的外角和定理: 多边形的外角和都是
n边形的对角线: 一个顶点有条对角线,共有条对角线 以六边形为例,每个顶点有6条对角线.
注意:不特别强调多边形都指凸多边形,凸多边形的每个内角都小于.
初出茅庐
主线7 多边形的规律
(1)如右图,小明从点出发,向前走米,左拐,再向前走米,再左拐,如此下去,小明能否回到出发点?如果能,第一次回到出发点共走了多少路程?
(2)m边形的一个顶点有7条对角线,n边形没有对角线,k边形对角线条数等于边数,则 .
(3)幼儿园的小朋友们打算选择一种形状、大小都相同的多边形塑胶板铺活动室的地面,为了保证铺地时既无缝隙又不重叠,请你告诉他们下面形状的塑胶板可以选择的是( ).
①三角形;②四边形;③正五边形;④正六边形;⑤正八边形.
A.③④⑤
B.①②④
C.①④
D.①③④⑤
【答案】(1)能,;(2)18;(3)B
能力觉醒
主线8 多边形的应用
(1)一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为_______
(2)如图,已知,则是______度
(3)能否同时用正三角形和正四边形镶嵌?如果可以,请写出具体的镶嵌方法.
【答案】(1)5或6或7;(2)140°;(3)3个正三角形加上2个正四边形.
终极试炼
主线9 角度计算
如图,,则n = ____
【答案】n=6.
法一:连接BF,
等于五角星ABDFG的内角和加上四边形BCEF的内角和,
五角星ABDFG的内角和为180°,四边形BCEF的内角和为360°,
故,∴n=6
法二:连接BE、GE,设AF与DG相交于点H,与BG相交于点M,与EG相交于点N
由外角性质的:
在△ADH中,,
在△MNG中,,
在△EFN中,
∴= △BCE的三个内角 + 四边形BMNE的四个内角=540°
∴n=6
课后竞技场
日常任务
任务1具备下列条件的三角形中,不是直角三角形的是( )
A. B.
C. D.,
【答案】D
任务2 如图,在中,,若沿图中虚线剪去,则等于( )
A. B. C. D.
【答案】B
任务3 如图所示,若,,,则等于( )
A.120° B.115° C.110° D.105°
【答案】B
任务4
(1)一个正多边形的外角与它相邻的内角之比为1:4,那么这个多边形的边数为( ).
A.8 B.9 C.10 D.12
【答案】C
(2)已知一个多边形的对角线的条数为边数的倍,求该多边形的边数.
【答案】
6
7
