2021-2022学年冀教版八年级数学上册17.3勾股定理 同步达标测评(Word版 含答案)
文档属性
| 名称 | 2021-2022学年冀教版八年级数学上册17.3勾股定理 同步达标测评(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 359.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 21:07:37 | ||
图片预览



文档简介
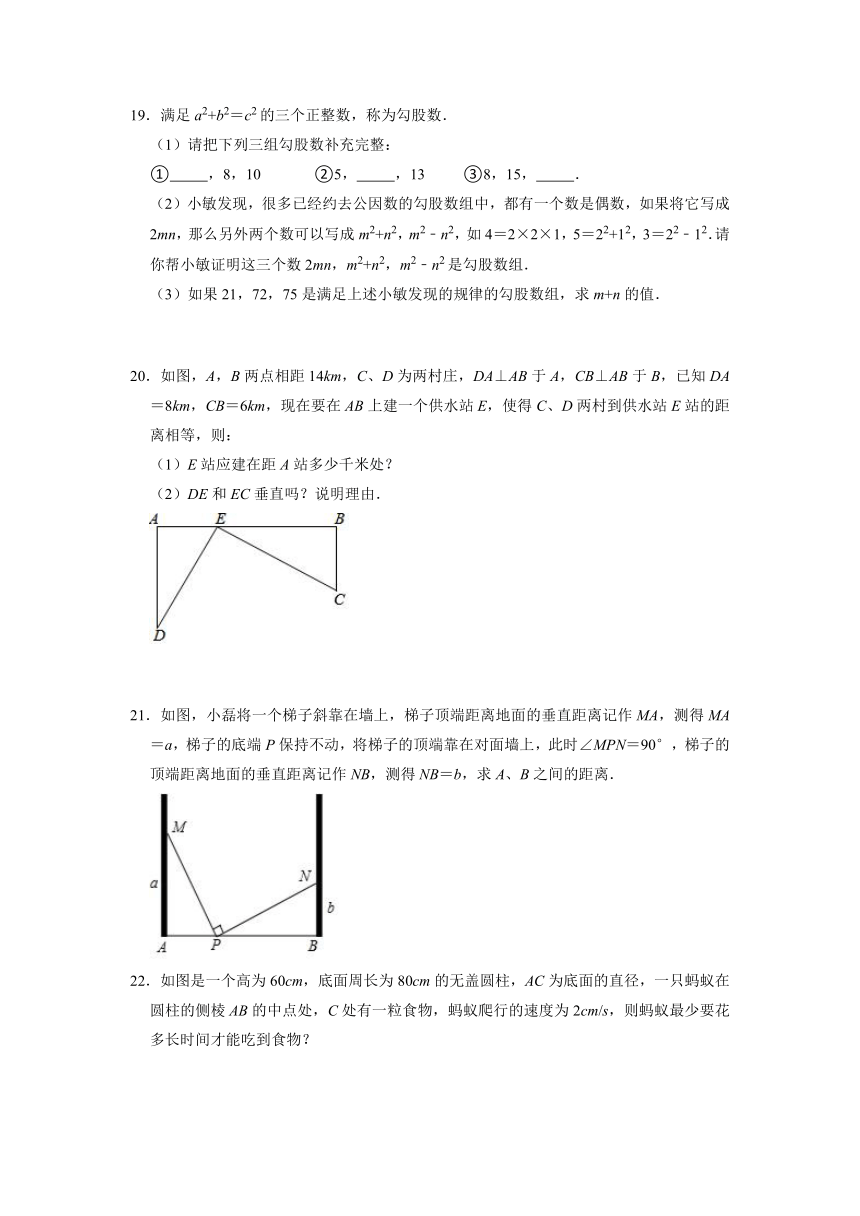
2021-2022学年冀教版八年级数学上册《17.3勾股定理》同步达标测评(附答案)
一.选择题(共10小题,满分40分)
1.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=12,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是( )
A.148 B.100 C.196 D.144
2.如图,在△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,BC=8cm,AC=6cm,则BD的长为( )
A.3cm B.4cm C.5cm D.6cm
3.如图,在等腰Rt△ACD中,∠ACD=90°,AC=DC,且AD=2,以边AD、AC、CD为直径画半圆,其中所得两个月形图案AGCE和DHCF(图中阴影部分)的面积之和等于( )
A.8 B.4 C.4 D.2
4.满足下列条件的△ABC中,不是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3 B.AC=1,BC=2,AB=
C.AC=6,BC=8,AB=10 D.AC=,BC=2,AB=
5.△ABC的三边长分别为a,b,c,由下列条件不能判断△ABC是直角三角形的是( )
A.∠A=2∠B=3∠C B.∠A=∠C﹣∠B
C.a:b:c=1::2 D.a2=(b+c)(b﹣c)
6.下面四组数中是勾股数的有( )
(1)1.5,2.5,2;(2),,2;(3)12,16,20;(4)0.5,1.2,1.3.
A.1组 B.2组 C.3组 D.4组
7.《九章算术》中的“折竹抵地”问题:今有竹高二丈,末折抵地,去根九尺,问折高者几何?意思是一根竹子,原高两丈(一丈=10尺),一阵风将竹子折断,其竹稍恰好抵地,抵地处离竹子底部9尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2﹣9=(20﹣x)2 B.x2﹣92=(20﹣x)2
C.x2+9=(20﹣x)2 D.x2+92=(20﹣x)2
8.如图,从旗杆AB的顶端A向地面拉一条绳子,绳子底端恰好在地面P处,若旗杆AB=10.2m,则绳子AP的长度不可能是( )
A.12m B.11m C.10.3m D.10m
9.如图,已知圆柱底面的周长为8dm,圆柱高为3dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为( )dm.
A.11 B. C. D.10
10.如图,长方体的长为8,宽为10,高为6,点B离点C的距离为2,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A. B. C. D.
二.填空题(共5小题,满分20分)
11.如图,在4×4的网格中,每个小正方形的边长均为1,点A、B、C都在格点上,则下列结论:①AB=2;②∠BAC=90°;③△ABC的面积为10;④点A到直线BC的距离是2,其中正确的是 .(填序号)
12.如图所示,ABCD是长方形地面,长AB=20m,宽AD=10m.中间竖有一堵砖墙高MN=2m.一只蚂蚱从A点爬到C点,它必须翻过中间那堵墙,则它至少要走 m的路程.
13.△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,下列条件中能判断出是△ABC直角三角形的有 .
(1)∠A:∠B:∠C=3:4:5;(2)a:b:c=5:4:3;(3)a2+b2=c2;(4)∠A=90°﹣∠B;(5)∠A+∠B=∠C.
14.如图所示的网格是正方形网格,A,B,C是网格线交点,则∠ABC+∠BAC= °.
15.如图,长方体盒子的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着盒子的表面从点A到点B.
(1)蚂蚁爬行的最短距离是 cm;
(2)若从C处想盒子里面插入一根吸管,要使吸管不落入盒子中,吸管应不少于 cm.
三.解答题(共8小题,满分60分)
16.用四个完全相同的直角三角形(如图1)拼成一大一小两个正方形(如图2),直角三角形的两条直角边分别是a、b(a>b),斜边长为ccm,请解答:
(1)图2中间小正方形的周长 ,大正方形的边长为 .
(2)用两种方法表示图2正方形的面积.(用含a,b,c)
①S= ;
②S= ;
(3)利用(2)小题的结果写出a、b、c三者之间的一个等式 .
(4)根据第(3)小题的结果,解决下面的问题:
已知直角三角形的两条直角边长分为是a=8,b=6,求斜边c的值.
17.如图,每小个正方形的边长都是1,每个小正方形的顶点称格点,△ABC的顶点都是在格点上.
(1)求△ABC的周长;
(2)求△ABC的面积.
18.如图,在正方形网格中,每个小正方形的边长都是1,四边形ABCD的四个顶点都在格线的交点上.解答下列问题:
(1)四边形ABCD的周长是 ,面积是 .
(2)连接AC,请判断△ADC和△ABC是什么特殊形状的三角形?并说明理由.
19.满足a2+b2=c2的三个正整数,称为勾股数.
(1)请把下列三组勾股数补充完整:
① ,8,10 ②5, ,13 ③8,15, .
(2)小敏发现,很多已经约去公因数的勾股数组中,都有一个数是偶数,如果将它写成2mn,那么另外两个数可以写成m2+n2,m2﹣n2,如4=2×2×1,5=22+12,3=22﹣12.请你帮小敏证明这三个数2mn,m2+n2,m2﹣n2是勾股数组.
(3)如果21,72,75是满足上述小敏发现的规律的勾股数组,求m+n的值.
20.如图,A,B两点相距14km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现在要在AB上建一个供水站E,使得C、D两村到供水站E站的距离相等,则:
(1)E站应建在距A站多少千米处?
(2)DE和EC垂直吗?说明理由.
21.如图,小磊将一个梯子斜靠在墙上,梯子顶端距离地面的垂直距离记作MA,测得MA=a,梯子的底端P保持不动,将梯子的顶端靠在对面墙上,此时∠MPN=90°,梯子的顶端距离地面的垂直距离记作NB,测得NB=b,求A、B之间的距离.
22.如图是一个高为60cm,底面周长为80cm的无盖圆柱,AC为底面的直径,一只蚂蚁在圆柱的侧棱AB的中点处,C处有一粒食物,蚂蚁爬行的速度为2cm/s,则蚂蚁最少要花多长时间才能吃到食物?
23.仔细阅读,解答下列问题
(1)有一长方体的食物包装纸盒如图(1),已知长方体的底面长为12,宽为9,高为5,一只蚂蚁想从底面A处爬到B处去吃食物,请问:蚂蚁爬行的最短距离是多少?
(2)如图(2),圆柱形容器的高为1.2米,底面周长为1米,在容器内壁离容器底部0.3米的点B处有一只蚊子,此处一只壁虎正好在容器外壁离容器上沿0.3米与蚊子相对的点A处,求壁虎捕捉到蚊子的最短路程是多少?(容器厚度忽略不计).
参考答案
一.选择题(共10小题,满分40分)
1.解:设将CA延长到点D,连接BD,
根据题意,得CD=12×2=24,BC=7,
∵∠BCD=90°,
∴BC2+CD2=BD2,即72+242=BD2,
∴BD=25,
∴AD+BD=12+25=37,
∴这个风车的外围周长是37×4=148.
故选:A.
2.解:过D作DE⊥AB于E,
在△ABC中,∠ACB=90°,BC=8cm,AC=6cm,
∴AB=(cm),
∵,
∵AD平分∠BAC交BC于点D,DE⊥AB,∠ACB=90°,
∴DE=CD,
∴,
∴CD=3(cm),
∴BD=BC﹣DC=8﹣3=5(cm),
故选:C.
3.解:在等腰Rt△ACD中,∠ACD=90°,AC=DC,AD=2,
∴AC2+DC2=AD2=8,
∴AC=CD=2,
∴S△ACD=AC DC=2,
∴S阴影=π()2+S△ACD﹣π()2
=π+2﹣π
=2,
故选:D.
4.解:A.∵∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,
∴∠C=×180°=90°,
∴△ABC是直角三角形,故本选项不符合题意;
B.∵AC=1,BC=2,AB=,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,故本选项不符合题意;
C.∵AC=6,BC=8,AB=10,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,故本选项不符合题意;
D.∵AC=,BC=2,AB=,
∴AC2+BC2≠AB2,
∴△ABC不是直角三角形,故本选项符合题意;
故选:D.
5.解:设△ABC中,∠A的对边是a,∠B的对边是b,∠C的对边是c,
A.∵∠A=2∠B=3∠C,
∴∠B=A,∠C=A,
∵∠A+∠B+∠C=180°,
∴∠A+A+A=180°,
解得:∠A=()°,
∴△ABC不是直角三角形,故本选项符合题意;
B.∵∠A=∠C﹣∠B,
∴∠A+∠B=∠C,
∵∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故本选项不符合题意;
C.∵a:b:c=1::2,
∴a2+b2=c2,
∴∠C=90°,
∴△ABC是直角三角形,故本选项不符合题意;
D∵a2=(b+c)(b﹣c),
∴a2=b2﹣c2,
即a2+c2=b2,
∴∠B=90°,
∴△ABC是直角三角形,故本选项不符合题意;
故选:A.
6.解:(1)1.52+22=2.52,但不是正整数,故错误;
(2)()2+()2=22,能构成直角三角形,但不是整数,故错误;
(3)122+162=202,三边是整数,同时能构成直角三角形,故正确;
(4)0.52+1.22=1.32,但不是正整数,故错误.
故选:A.
7.解:如图,设折断处离地面的高度为x尺,则AB=(20﹣x)尺,BC=9尺,
在Rt△ABC中,AC2+BC2=AB2,即x2+92=(20﹣x)2.
故选:D.
8.解:∵旗杆的高度为AB=10.2米,
∴AP>AB,
∴绳子AP的长度不可能是:10米.
故选:D.
9.解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
∵圆柱底面的周长为4dm,圆柱高为3dm,
∴AB=3dm,BC=BC′=4dm,
∴AC2=32+42=25,
∴AC=5(dm).
∴这圈金属丝的周长最小为2AC=10(dm).
故选:D.
10.解:如图1:(1)AB===6;
(2)AB===2;
(3)AB==2.
所以需要爬行的最短距离是2,
故选:A.
二.填空题(共5小题,满分20分)
11.解:①∵AB2=22+42=20,
∴AB=2,故正确;
②∵AC2=12+22=5,AB2=22+42=20,BC2=32+42=25,
∴AC2+AB2=BC2,
∴∠BAC=90°,故正确;
③S△ABC=4×4﹣×3×4﹣×1×2﹣×2×4=5,故错误;
④设点A到直线BC的距离为h,
∵BC2=32+42=25,
∴BC=5,
则×5×h=5,
解得,h=2,即点A到直线BC的距离是2,故正确;
故答案为:①②④.
12.解:如图所示,将图展开,图形长度增加2MN,
原图长度增加4米,则AB=20+4=24m,
连接AC,
∵四边形ABCD是长方形,AB=24m,宽AD=10m,
∴AC====26m,
∴蚂蚱从A点爬到C点,它至少要走26m的路程.
故答案为:26m.
13.解:(1)∵∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,
∴最大角∠C=×180°=75°,
∴△ABC不是直角三角形;
(2)∵a:b:c=5:4:3,
∴b2+c2=a2,
∴∠A=90°,
∴△ABC是直角三角形;
(3)∵a2+b2=c2,
∴∠C=90°,
∴△ABC是直角三角形;
(4)∵∠A=90°﹣∠B,
∴∠A+∠B=90°,
∴∠C=180°﹣(∠A+∠B)=90°,
∴△ABC是直角三角形;
(5)∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,
所以能判断出是△ABC直角三角形的有(2)(3)(4)(5),
故答案为:(2)(3)(4)(5).
14.解:设小正方形的边长是1,则AO=CO=3,
所以△AOC是等腰直角三角形,
∴∠ACO=∠OAC=45°,
∵∠ABC+∠BAC=∠ACO,
∴∠ABC+∠BAC=45°,
故答案为:45.
15.解:(1)只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴BD=CD+BC=10+5=15(cm),AD=20(cm),
在直角三角形ABD中,根据勾股定理得:
∴AB===25(cm);
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴BD=CD+BC=20+5=25(cm),AD=10cm,
在直角三角形ABD中,根据勾股定理得:
∴AB===5(cm);
只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴AC=CD+AD=20+10=30(cm),
在直角三角形ABC中,根据勾股定理得:
∴AB===5(cm);
∵25<5<5,
∴蚂蚁爬行的最短距离是25(cm).
故答案为:25;
(2)盒子底面对角长为=,
当吸管、长方体的高及底面对角线的长正好构成直角三角形时,插入盒子内的吸管长度最长,
则吸管长度为:=5(cm),
∴吸管应不少于5cm.
故答案为:5.
三.解答题(共8小题,满分60分)
16.解:(1)图2中间小正方形的周长4c,大正方形的边长为(a+b),
故答案为:4c;a+b;
(2)图2正方形的面积S=(a+b)2或S=2ab+c2,
故答案为:(a+b)2或2ab+c2;
(3)∵(a+b)2=a2+2ab+b2,
∴a2+b2=c2.
故答案为:a2+b2=c2;
(4)∵c2=a2+b2=82+62=100,
∴c=10(负值不合题意,舍去).
17.解:(1)由勾股定理得:,,,
∴△ABC的周长=;
(2)由(1)可知,AC2+AB2=()2+()2=20,BC2=(2)2=20,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∴.
18.解:(1)由勾股定理得:AD==,DC==2,BC==5,
∵AB=6,
∴四边形ABCD的周长是AD+CD+BC+AB=+2+5+6=11+3,
四边形ABCD的面积S=7×4﹣﹣﹣=17,
故答案为:11+3,17;
(2)△ADC是直角三角形,△ABC是等腰三角形,
理由是:连接AC,
由勾股定理得:AC==5,
∵AD=,CD=2,
∴AD2+CD2=AC2,
∴△ADC是直角三角形(∠ADC=90°),
∵BC=5,AC=5,
∴AC=BC,
∵AB=6,
∴△ABC是等腰三角形
19.解:(1)①6,8,10; ②5.12,13;③8,15,17.
故答案为:6,12,17;
(2)证明:∵(m2﹣n2)2+(2mn)2=m4+n4﹣2m2n2+4m2n2=m4+n4+2m2n2,
(m2+n2)2=m4+n4+2m2n2,
∴(m2﹣n2)2+(2mn)2=(m2+n2)2,
∴m2﹣n2,m2+n2,2mn是勾股数;
(3)化简得:7,24,25,
∵偶数24=2×3×4,25=42+32,7=42﹣32,
∴m=4,n=3,
∴m+n=7.
20.解:(1)设AE=xkm,
∵C、D两村到E站的距离相等,∴DE=CE,即DE2=CE2,
由勾股定理,得82+x2=62+(14﹣x)2,
解得:x=6.
故E点应建在距A站6千米处;
(2)DE⊥CD,理由如下:
在Rt△DAE和Rt△CBE中,
,
∴Rt△DAE≌Rt△CBE(HL),
∴∠D=∠BEC,
∵∠D+∠AED=90°,
∴∠BEC+∠AED=90°,
∴∠DEC=90°,
∴DE⊥CD.
21.解:∵∠MPN=90°,
∴∠APM+∠BPN=90°,
∵∠APM+∠AMP=90°,
∴∠AMP=∠BPN.
在△AMP与△BPN中,
,
∴△AMP≌△BPN(AAS),
∴MA=PB=a,PA=NB=b,
∴AB=PA+PB=a+b.
22.解:如图在侧面展开图中,AD=30cm,AC=40cm,
∴CD==50,
∵=25,
∴蚂蚁最少要花25s才能吃到食物.
23.解:(1)第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是12cm和14cm,
则所走的最短线段是 =2,
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是9cm和17cm,
所以走的最短线段是=cm;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是21cm和5cm,
所以走的最短线段是=cm;
三种情况比较而言,第一种情况最短,
∴蚂蚁爬行的最短距离是2cm;
(2)如图:∵高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,
此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,
∴A′D=0.5m,BD=1.2m,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B=
=
=1.3(m).
答:壁虎捕捉到蚊子的最短路程是1.3m.
一.选择题(共10小题,满分40分)
1.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=12,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是( )
A.148 B.100 C.196 D.144
2.如图,在△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,BC=8cm,AC=6cm,则BD的长为( )
A.3cm B.4cm C.5cm D.6cm
3.如图,在等腰Rt△ACD中,∠ACD=90°,AC=DC,且AD=2,以边AD、AC、CD为直径画半圆,其中所得两个月形图案AGCE和DHCF(图中阴影部分)的面积之和等于( )
A.8 B.4 C.4 D.2
4.满足下列条件的△ABC中,不是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3 B.AC=1,BC=2,AB=
C.AC=6,BC=8,AB=10 D.AC=,BC=2,AB=
5.△ABC的三边长分别为a,b,c,由下列条件不能判断△ABC是直角三角形的是( )
A.∠A=2∠B=3∠C B.∠A=∠C﹣∠B
C.a:b:c=1::2 D.a2=(b+c)(b﹣c)
6.下面四组数中是勾股数的有( )
(1)1.5,2.5,2;(2),,2;(3)12,16,20;(4)0.5,1.2,1.3.
A.1组 B.2组 C.3组 D.4组
7.《九章算术》中的“折竹抵地”问题:今有竹高二丈,末折抵地,去根九尺,问折高者几何?意思是一根竹子,原高两丈(一丈=10尺),一阵风将竹子折断,其竹稍恰好抵地,抵地处离竹子底部9尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2﹣9=(20﹣x)2 B.x2﹣92=(20﹣x)2
C.x2+9=(20﹣x)2 D.x2+92=(20﹣x)2
8.如图,从旗杆AB的顶端A向地面拉一条绳子,绳子底端恰好在地面P处,若旗杆AB=10.2m,则绳子AP的长度不可能是( )
A.12m B.11m C.10.3m D.10m
9.如图,已知圆柱底面的周长为8dm,圆柱高为3dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为( )dm.
A.11 B. C. D.10
10.如图,长方体的长为8,宽为10,高为6,点B离点C的距离为2,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A. B. C. D.
二.填空题(共5小题,满分20分)
11.如图,在4×4的网格中,每个小正方形的边长均为1,点A、B、C都在格点上,则下列结论:①AB=2;②∠BAC=90°;③△ABC的面积为10;④点A到直线BC的距离是2,其中正确的是 .(填序号)
12.如图所示,ABCD是长方形地面,长AB=20m,宽AD=10m.中间竖有一堵砖墙高MN=2m.一只蚂蚱从A点爬到C点,它必须翻过中间那堵墙,则它至少要走 m的路程.
13.△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,下列条件中能判断出是△ABC直角三角形的有 .
(1)∠A:∠B:∠C=3:4:5;(2)a:b:c=5:4:3;(3)a2+b2=c2;(4)∠A=90°﹣∠B;(5)∠A+∠B=∠C.
14.如图所示的网格是正方形网格,A,B,C是网格线交点,则∠ABC+∠BAC= °.
15.如图,长方体盒子的长为15cm,宽为10cm,高为20cm,点B距离C点5cm,一只蚂蚁如果要沿着盒子的表面从点A到点B.
(1)蚂蚁爬行的最短距离是 cm;
(2)若从C处想盒子里面插入一根吸管,要使吸管不落入盒子中,吸管应不少于 cm.
三.解答题(共8小题,满分60分)
16.用四个完全相同的直角三角形(如图1)拼成一大一小两个正方形(如图2),直角三角形的两条直角边分别是a、b(a>b),斜边长为ccm,请解答:
(1)图2中间小正方形的周长 ,大正方形的边长为 .
(2)用两种方法表示图2正方形的面积.(用含a,b,c)
①S= ;
②S= ;
(3)利用(2)小题的结果写出a、b、c三者之间的一个等式 .
(4)根据第(3)小题的结果,解决下面的问题:
已知直角三角形的两条直角边长分为是a=8,b=6,求斜边c的值.
17.如图,每小个正方形的边长都是1,每个小正方形的顶点称格点,△ABC的顶点都是在格点上.
(1)求△ABC的周长;
(2)求△ABC的面积.
18.如图,在正方形网格中,每个小正方形的边长都是1,四边形ABCD的四个顶点都在格线的交点上.解答下列问题:
(1)四边形ABCD的周长是 ,面积是 .
(2)连接AC,请判断△ADC和△ABC是什么特殊形状的三角形?并说明理由.
19.满足a2+b2=c2的三个正整数,称为勾股数.
(1)请把下列三组勾股数补充完整:
① ,8,10 ②5, ,13 ③8,15, .
(2)小敏发现,很多已经约去公因数的勾股数组中,都有一个数是偶数,如果将它写成2mn,那么另外两个数可以写成m2+n2,m2﹣n2,如4=2×2×1,5=22+12,3=22﹣12.请你帮小敏证明这三个数2mn,m2+n2,m2﹣n2是勾股数组.
(3)如果21,72,75是满足上述小敏发现的规律的勾股数组,求m+n的值.
20.如图,A,B两点相距14km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现在要在AB上建一个供水站E,使得C、D两村到供水站E站的距离相等,则:
(1)E站应建在距A站多少千米处?
(2)DE和EC垂直吗?说明理由.
21.如图,小磊将一个梯子斜靠在墙上,梯子顶端距离地面的垂直距离记作MA,测得MA=a,梯子的底端P保持不动,将梯子的顶端靠在对面墙上,此时∠MPN=90°,梯子的顶端距离地面的垂直距离记作NB,测得NB=b,求A、B之间的距离.
22.如图是一个高为60cm,底面周长为80cm的无盖圆柱,AC为底面的直径,一只蚂蚁在圆柱的侧棱AB的中点处,C处有一粒食物,蚂蚁爬行的速度为2cm/s,则蚂蚁最少要花多长时间才能吃到食物?
23.仔细阅读,解答下列问题
(1)有一长方体的食物包装纸盒如图(1),已知长方体的底面长为12,宽为9,高为5,一只蚂蚁想从底面A处爬到B处去吃食物,请问:蚂蚁爬行的最短距离是多少?
(2)如图(2),圆柱形容器的高为1.2米,底面周长为1米,在容器内壁离容器底部0.3米的点B处有一只蚊子,此处一只壁虎正好在容器外壁离容器上沿0.3米与蚊子相对的点A处,求壁虎捕捉到蚊子的最短路程是多少?(容器厚度忽略不计).
参考答案
一.选择题(共10小题,满分40分)
1.解:设将CA延长到点D,连接BD,
根据题意,得CD=12×2=24,BC=7,
∵∠BCD=90°,
∴BC2+CD2=BD2,即72+242=BD2,
∴BD=25,
∴AD+BD=12+25=37,
∴这个风车的外围周长是37×4=148.
故选:A.
2.解:过D作DE⊥AB于E,
在△ABC中,∠ACB=90°,BC=8cm,AC=6cm,
∴AB=(cm),
∵,
∵AD平分∠BAC交BC于点D,DE⊥AB,∠ACB=90°,
∴DE=CD,
∴,
∴CD=3(cm),
∴BD=BC﹣DC=8﹣3=5(cm),
故选:C.
3.解:在等腰Rt△ACD中,∠ACD=90°,AC=DC,AD=2,
∴AC2+DC2=AD2=8,
∴AC=CD=2,
∴S△ACD=AC DC=2,
∴S阴影=π()2+S△ACD﹣π()2
=π+2﹣π
=2,
故选:D.
4.解:A.∵∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,
∴∠C=×180°=90°,
∴△ABC是直角三角形,故本选项不符合题意;
B.∵AC=1,BC=2,AB=,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,故本选项不符合题意;
C.∵AC=6,BC=8,AB=10,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,故本选项不符合题意;
D.∵AC=,BC=2,AB=,
∴AC2+BC2≠AB2,
∴△ABC不是直角三角形,故本选项符合题意;
故选:D.
5.解:设△ABC中,∠A的对边是a,∠B的对边是b,∠C的对边是c,
A.∵∠A=2∠B=3∠C,
∴∠B=A,∠C=A,
∵∠A+∠B+∠C=180°,
∴∠A+A+A=180°,
解得:∠A=()°,
∴△ABC不是直角三角形,故本选项符合题意;
B.∵∠A=∠C﹣∠B,
∴∠A+∠B=∠C,
∵∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故本选项不符合题意;
C.∵a:b:c=1::2,
∴a2+b2=c2,
∴∠C=90°,
∴△ABC是直角三角形,故本选项不符合题意;
D∵a2=(b+c)(b﹣c),
∴a2=b2﹣c2,
即a2+c2=b2,
∴∠B=90°,
∴△ABC是直角三角形,故本选项不符合题意;
故选:A.
6.解:(1)1.52+22=2.52,但不是正整数,故错误;
(2)()2+()2=22,能构成直角三角形,但不是整数,故错误;
(3)122+162=202,三边是整数,同时能构成直角三角形,故正确;
(4)0.52+1.22=1.32,但不是正整数,故错误.
故选:A.
7.解:如图,设折断处离地面的高度为x尺,则AB=(20﹣x)尺,BC=9尺,
在Rt△ABC中,AC2+BC2=AB2,即x2+92=(20﹣x)2.
故选:D.
8.解:∵旗杆的高度为AB=10.2米,
∴AP>AB,
∴绳子AP的长度不可能是:10米.
故选:D.
9.解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
∵圆柱底面的周长为4dm,圆柱高为3dm,
∴AB=3dm,BC=BC′=4dm,
∴AC2=32+42=25,
∴AC=5(dm).
∴这圈金属丝的周长最小为2AC=10(dm).
故选:D.
10.解:如图1:(1)AB===6;
(2)AB===2;
(3)AB==2.
所以需要爬行的最短距离是2,
故选:A.
二.填空题(共5小题,满分20分)
11.解:①∵AB2=22+42=20,
∴AB=2,故正确;
②∵AC2=12+22=5,AB2=22+42=20,BC2=32+42=25,
∴AC2+AB2=BC2,
∴∠BAC=90°,故正确;
③S△ABC=4×4﹣×3×4﹣×1×2﹣×2×4=5,故错误;
④设点A到直线BC的距离为h,
∵BC2=32+42=25,
∴BC=5,
则×5×h=5,
解得,h=2,即点A到直线BC的距离是2,故正确;
故答案为:①②④.
12.解:如图所示,将图展开,图形长度增加2MN,
原图长度增加4米,则AB=20+4=24m,
连接AC,
∵四边形ABCD是长方形,AB=24m,宽AD=10m,
∴AC====26m,
∴蚂蚱从A点爬到C点,它至少要走26m的路程.
故答案为:26m.
13.解:(1)∵∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,
∴最大角∠C=×180°=75°,
∴△ABC不是直角三角形;
(2)∵a:b:c=5:4:3,
∴b2+c2=a2,
∴∠A=90°,
∴△ABC是直角三角形;
(3)∵a2+b2=c2,
∴∠C=90°,
∴△ABC是直角三角形;
(4)∵∠A=90°﹣∠B,
∴∠A+∠B=90°,
∴∠C=180°﹣(∠A+∠B)=90°,
∴△ABC是直角三角形;
(5)∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,
所以能判断出是△ABC直角三角形的有(2)(3)(4)(5),
故答案为:(2)(3)(4)(5).
14.解:设小正方形的边长是1,则AO=CO=3,
所以△AOC是等腰直角三角形,
∴∠ACO=∠OAC=45°,
∵∠ABC+∠BAC=∠ACO,
∴∠ABC+∠BAC=45°,
故答案为:45.
15.解:(1)只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴BD=CD+BC=10+5=15(cm),AD=20(cm),
在直角三角形ABD中,根据勾股定理得:
∴AB===25(cm);
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴BD=CD+BC=20+5=25(cm),AD=10cm,
在直角三角形ABD中,根据勾股定理得:
∴AB===5(cm);
只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴AC=CD+AD=20+10=30(cm),
在直角三角形ABC中,根据勾股定理得:
∴AB===5(cm);
∵25<5<5,
∴蚂蚁爬行的最短距离是25(cm).
故答案为:25;
(2)盒子底面对角长为=,
当吸管、长方体的高及底面对角线的长正好构成直角三角形时,插入盒子内的吸管长度最长,
则吸管长度为:=5(cm),
∴吸管应不少于5cm.
故答案为:5.
三.解答题(共8小题,满分60分)
16.解:(1)图2中间小正方形的周长4c,大正方形的边长为(a+b),
故答案为:4c;a+b;
(2)图2正方形的面积S=(a+b)2或S=2ab+c2,
故答案为:(a+b)2或2ab+c2;
(3)∵(a+b)2=a2+2ab+b2,
∴a2+b2=c2.
故答案为:a2+b2=c2;
(4)∵c2=a2+b2=82+62=100,
∴c=10(负值不合题意,舍去).
17.解:(1)由勾股定理得:,,,
∴△ABC的周长=;
(2)由(1)可知,AC2+AB2=()2+()2=20,BC2=(2)2=20,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∴.
18.解:(1)由勾股定理得:AD==,DC==2,BC==5,
∵AB=6,
∴四边形ABCD的周长是AD+CD+BC+AB=+2+5+6=11+3,
四边形ABCD的面积S=7×4﹣﹣﹣=17,
故答案为:11+3,17;
(2)△ADC是直角三角形,△ABC是等腰三角形,
理由是:连接AC,
由勾股定理得:AC==5,
∵AD=,CD=2,
∴AD2+CD2=AC2,
∴△ADC是直角三角形(∠ADC=90°),
∵BC=5,AC=5,
∴AC=BC,
∵AB=6,
∴△ABC是等腰三角形
19.解:(1)①6,8,10; ②5.12,13;③8,15,17.
故答案为:6,12,17;
(2)证明:∵(m2﹣n2)2+(2mn)2=m4+n4﹣2m2n2+4m2n2=m4+n4+2m2n2,
(m2+n2)2=m4+n4+2m2n2,
∴(m2﹣n2)2+(2mn)2=(m2+n2)2,
∴m2﹣n2,m2+n2,2mn是勾股数;
(3)化简得:7,24,25,
∵偶数24=2×3×4,25=42+32,7=42﹣32,
∴m=4,n=3,
∴m+n=7.
20.解:(1)设AE=xkm,
∵C、D两村到E站的距离相等,∴DE=CE,即DE2=CE2,
由勾股定理,得82+x2=62+(14﹣x)2,
解得:x=6.
故E点应建在距A站6千米处;
(2)DE⊥CD,理由如下:
在Rt△DAE和Rt△CBE中,
,
∴Rt△DAE≌Rt△CBE(HL),
∴∠D=∠BEC,
∵∠D+∠AED=90°,
∴∠BEC+∠AED=90°,
∴∠DEC=90°,
∴DE⊥CD.
21.解:∵∠MPN=90°,
∴∠APM+∠BPN=90°,
∵∠APM+∠AMP=90°,
∴∠AMP=∠BPN.
在△AMP与△BPN中,
,
∴△AMP≌△BPN(AAS),
∴MA=PB=a,PA=NB=b,
∴AB=PA+PB=a+b.
22.解:如图在侧面展开图中,AD=30cm,AC=40cm,
∴CD==50,
∵=25,
∴蚂蚁最少要花25s才能吃到食物.
23.解:(1)第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是12cm和14cm,
则所走的最短线段是 =2,
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是9cm和17cm,
所以走的最短线段是=cm;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是21cm和5cm,
所以走的最短线段是=cm;
三种情况比较而言,第一种情况最短,
∴蚂蚁爬行的最短距离是2cm;
(2)如图:∵高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,
此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,
∴A′D=0.5m,BD=1.2m,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B=
=
=1.3(m).
答:壁虎捕捉到蚊子的最短路程是1.3m.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
