2021-2022学年冀教版八年级数学上册16.2线段的垂直平分线 同步达标训练(Word版 含答案)
文档属性
| 名称 | 2021-2022学年冀教版八年级数学上册16.2线段的垂直平分线 同步达标训练(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 286.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 21:10:16 | ||
图片预览

文档简介
2021-2022学年冀教版八年级数学上册《16.2线段的垂直平分线》同步达标训练(附答案)
一、选择题
1.如图,△ABC中,AB的垂直平分线DE分别与边AB,AC交于点D,点E,若△ABC与△BCE的周长分别是36cm和22cm,则AD的长是( )
A.7cm B.8cm C.10cm D.14cm
2.如图,△ABC中,∠B=40°,AC的垂直平分线交AC于D,交BC于E,且∠EAB:∠CAE=3:1,则∠C等于( )
A.28° B.25° C.22.5° D.20°
3.如图,△ABC中,∠BAC=130°,AB,AC的垂直平分线分别交BC于点E,F,与AB,AC分别交于点D,G,则∠EAF的度数为( )
A.65° B.60° C.70° D.80°
4.到三角形三个顶点距离都相等的点是( )
A.三角形的三条角平分线的交点
B.三角形的三边垂直平分线的交点
C.三角形的三条高线的交点
D.三角形的三条中线的交点
5.下列条件中,不能判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线的是( )
A.CA=CB,DA=DB B.CA=CB,CD⊥AB
C.CA=DA,CB=DB D.CA=CB,CD平分AB
6.如图,在△ABC中,直线l为边BC的垂直平分线,l交AC于点Q,∠ABC的角平分线与l相交于点P.若∠BAC=60°,∠ACP=24°,则∠PQC是( )
A.34° B.36° C.44° D.46°
7.如图,在Rt△ABC中,ED为AB的垂直平分线,连接CD,若∠B=52°,则∠ACD的度数为( )
A.38° B.48° C.52° D.42°
8.如图,△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,若△ABC周长为16,AC=6,则DC为( )
A.5 B.8 C.9 D.10
9.如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
A.2 B.4 C.6 D.8
10.如图,已知△ABC中,∠B=50°,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为( )
A.100° B.105° C.115° D.120°
11.如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=6,CF=2,则AC的长度为( )
A.6 B.7 C.8 D.9
12.已知,如图,DE垂直平分AB,交AB于点E,交BC于点D,△ACD的周长是13,BC=8,则AC的长是( )
A.6 B.5 C.4 D.3
13.如图,在△ABC中,线段AB的垂直平分线与AC相交于点D,连接BD,边AC的长为12cm,边BC的长为7cm,则△BCD的周长为( )
A.18cm B.19cm C.20cm D.21cm
14.如图,在△ABC中,∠C=90°,AC=6,BC=8,点P为AC上一点,PA=2,点D在AB上,且∠A=∠PDA,BD的垂直平分线交BC于点E,交BD于点F,连接DE,则线段DE的长为( )
A.4.75 B.5.25 C.6.5 D.7.75
二、填空题
15.如图Rt△ABC中,∠ACB=90°,AC=4,BC=9,ED垂直平分AB,△ACE周长= .
16.如图,△ABC中,D在BC边上,E在AC边上,且DE垂直平分AC.若△ABC的周长为21cm,△ABD的周长为13cm,则AE的长为 .
17.如图,在△ABC中,直线DE垂直平分BC,垂足为E,交AC于点D,若△ABD的周长为12,AB=5,则AC的长为 .
如图,线段AB、BC的垂直平分线l1、l2相交于点O,若∠1=38°,则∠AOC的度数为 .
19.如图,在△ABC中,BC边的垂直平分线交BC于D,交AB于E.若CE平分∠ACB,∠B=42°,则∠A= .
三、解答题
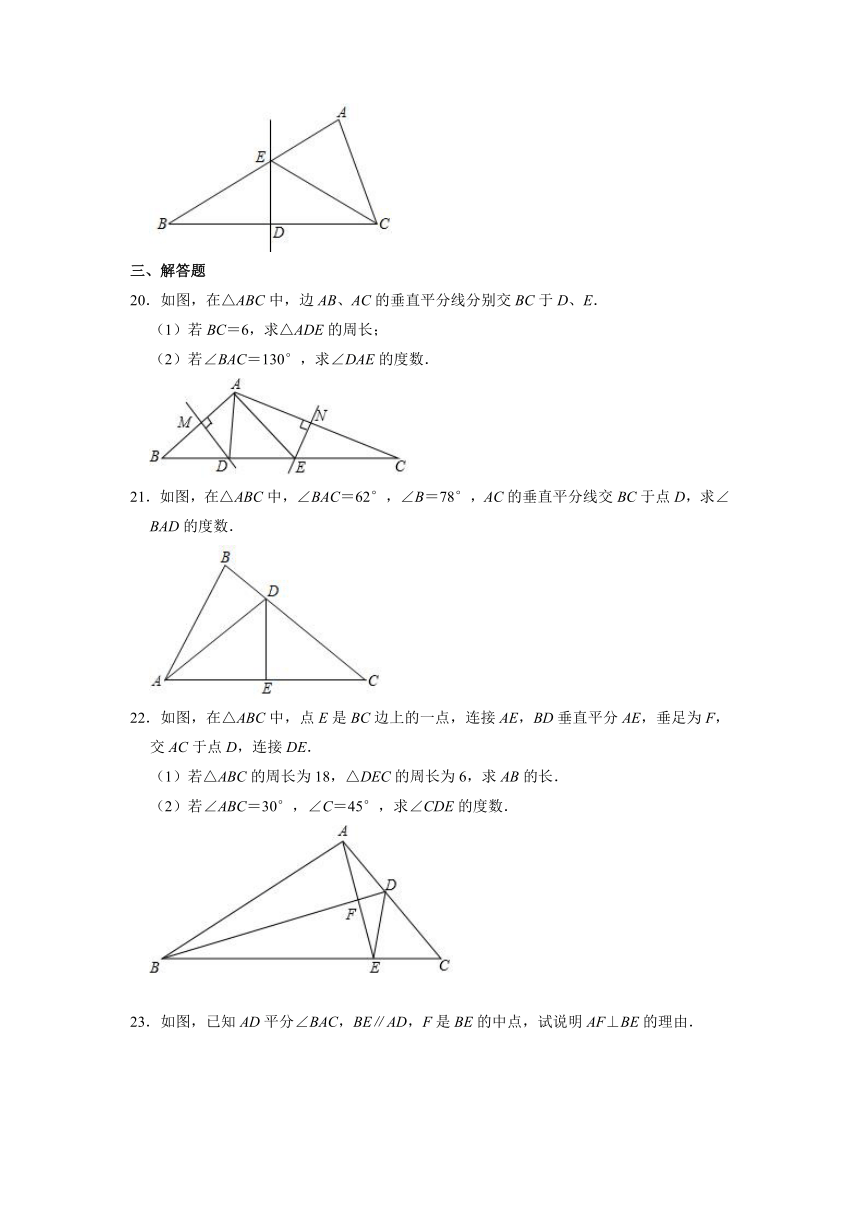
20.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=6,求△ADE的周长;
(2)若∠BAC=130°,求∠DAE的度数.
21.如图,在△ABC中,∠BAC=62°,∠B=78°,AC的垂直平分线交BC于点D,求∠BAD的度数.
22.如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D,连接DE.
(1)若△ABC的周长为18,△DEC的周长为6,求AB的长.
(2)若∠ABC=30°,∠C=45°,求∠CDE的度数.
23.如图,已知AD平分∠BAC,BE∥AD,F是BE的中点,试说明AF⊥BE的理由.
24.如图,Rt△ABC中,∠C=90°,直线DE是边AB的垂直平分线,连接BE.
(1)若∠A=35°,求∠CBE的度数;
(2)若AE=3,EC=1,求△ABC的面积.
25.如图,在△ABC中,AC的垂直平分线交AC于点D,交BC延长线交于点E,连接AE,如果∠B=50°,∠BAC=21°,求∠CAE的度数.
26.如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.求证:线段BF垂直平分线段AD.
参考答案
1.解:∵DE是AB的垂直平分线,
∴EA=EB,AD=BD=AB,
∵△EBC的周长是22cm,
∴BC+BE+EC=22cm,即AC+BC=22cm,
∵△ABC的周长是36cm,
∴AB+AC+BC=36cm,
∴AB=36﹣22=14(cm),
∴AD=AB=×14=7(cm).
故选:A.
2.解:设∠CAE=x,则∠EAB=3x.
∵AC的垂直平分线交AC于D,交BC于E,
∴AE=CE.
∴∠C=∠CAE=x.
根据三角形的内角和定理,得
∠C+∠BAC=180°﹣∠B,
即x+4x=140°,
∴x=28°.
则∠C=28°.
故选:A.
3.解:∵DE垂直平分AB,FG垂直平分AC,
∴EB=EA,FA=FC,
∴∠BAE=∠B,∠FAC=∠C,
∵△ABC中,∠BAC=130°,
∴∠B+∠C=50°,
∴∠BAE+∠FAC=50°,
∴∠EAF=∠BAC﹣(∠BAE+∠FAC)=80°;
故选:D.
4.解:∵到三角形的一边的两端点距离相等的点在这边的垂直平分线上,
∴到三角形三个顶点的距离都相等的点是这个三角形的三条边的垂直平分线的交点,
故选:B.
5.解:A、∵CA=CB,DA=DB,
∴直线CD是线段AB的垂直平分线;
B、∵CA=CB,CD⊥AB,
∴直线CD是线段AB的垂直平分线;
C、当CA=DA,CB=DB时,直线CD不一定是线段AB的垂直平分线;
D、∵CA=CB,CD平分AB,
∴直线CD是线段AB的垂直平分线,
故选:C.
6.解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵直线l是线段BC的垂直平分线,
∴BP=CP,
∴∠CBP=∠BCP,
∴∠ABP=∠BCP,
∵∠A+∠ACB+∠ABC=180°,∠A=60°,∠ACP=24°,
∴3∠ABP+24°+60°=180°,
∴∠ABP=32°,
∴∠PBC=∠PCB=32°,
∴∠PQC=×(180°﹣32°﹣32°)﹣24°=58°﹣24°=34°,
故选:A.
7.解:∵ED为AB的垂直平分线,
∴AD=BD,
∵∠ACB=90°,
∴CD=BD,
∴∠DCB=∠B,
∵∠B=52°,
∴∠DCB=52°,
∴∠ACD=90°﹣52°=38°,
故选:A.
8.解:∵△ABC周长为16,
∴AB+BC+AC=16,
∵AC=6,
∴AB+BC=10,
∵EF垂直平分AC,
∴EA=EC,
∵AB=AE,AD⊥BC,
∴BD=DE,
∴AB+BD=AE+DE=×(AB+BC)=5,
∴DC=DE+EC=AE+DE=5,
故选:A.
9.解:∵DE是AB的垂直平分线,AE=4,
∴EB=EA=4,
∴BC=EB+EC=4+2=6,
故选:C.
10.解:∵∠ABC=50°,
∴∠BAC+∠ACB=130°,
∵M在PA的中垂线上,N在PC的中垂线上,
∴AM=PM,PN=CN,
∴∠MAP=∠APM,∠CPN=∠PCN,
∵∠APC=180°﹣∠APM﹣∠CPN=180°﹣∠PAC﹣∠ACP,
∴∠MAP+∠PCN=∠PAC+∠ACP=×130°=65°,
∴∠APC=115°,
故选:C.
11.解:∵EF是AB的垂直平分线,BF=6,
∴FA=BF=6,
∴AC=FA+CF=6+2=8,
故选:C.
12.解:∵DE垂直平分AB,
∴DA=DB,
∵△ACD的周长是13,
∴AC+DA+CD=13,
∴AC+DB+CD=AC+BC=13,
∵BC=8,
∴AC=5,
故选:B.
13.解:∵线段AB的垂直平分线与AC相交于点D,
∴DA=DB,
∴△BCD的周长=BC+CD+DB=BC+CD+DA=BC+AC,
∵AC=12cm,BC=7cm,
∴△BCD的周长=BC+AC=12+7=19(cm),
故选:B.
14.解:过P点作PG⊥AD交与G点,
∵∠A=∠PDA,
∴G是AD的中点,
∵∠C=90°,AC=6,BC=8,
∴AB=10,
∵AP=2,
∴=,
∴AG=,
∴AD=,
∴BD=10﹣=,
∵BD的垂直平分线交BC,
∴DF=BF,
∴DF=,
∴DE=,
故选:A.
方法2:
解:∵∠C=90°,AC=6,BC=8,
∴AB=10,
∵AP=2,
∴PC=4,设CE=x,则BE=8﹣x,
∵∠A=∠PDA,
∴AP=PD=2,
∵BD的垂直平分线交BC,
∴DE=BE=8﹣x,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠PDA+∠EDF=90°,
∴∠PDE=90°,
在Rt△PEC中,PE2=PC2+CE2,
∴PE2=16+x2,
在Rt△PED中,PE2=PD2+DE2,
∴PE2=4+(8﹣x)2,
∴16+x2=4+(8﹣x)2,
∴x=,
∴DE=8﹣=,
故选:A.
15.解:∵ED垂直平分边AB,
∴EA=EB,
∴△ACE的周长=AC+EC+EA=AC+EC+EB=AC+BC,
∵AC=4,BC=9,
∴△ACE的周长=AC+BC=4+9=13,
故答案为:13.
16.解:∵DE是AC的垂直平分线,
∴DA=DC,AE=EC,
∵△ABC的周长为21cm,
∴AB+BC+AC=21cm,
∵△ABD的周长为13cm,
∴AB+BD+AD=AB+BD+DC=AB+BC=13(cm),
∴AC=8cm,
∴AE=4cm,
故答案为:4cm.
17.解:∵△ABD的周长为12,
∴AB+AD+BD=12,
∵DE垂直平分BC,
∴DB=DC,
∴AB+AD+DC=12,即AB+AC=12,
∵AB=5,
∴AC=7,
故答案为:7.
18.解:连接BO,并延长BO到P,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴AO=OB=OC,∠BDO=∠BEO=90°,
∴∠DOE+∠ABC=180°,
∵∠DOE+∠1=180°,
∴∠ABC=∠1=38°,
∵OA=OB=OC,
∴∠A=∠ABO,∠OBC=∠C,
∵∠AOP=∠A+∠ABO,∠COP=∠C+∠OBC,
∴∠AOC=∠AOP+∠COP=∠A+∠ABC+∠C=2×38°=76°;
故答案为:76°.
19.解:∵E在线段BC的垂直平分线上,
∴BE=CE,
∴∠ECB=∠B=42°,
∵CE平分∠ACB,
∴∠ACD=2∠ECB=84°,
又∵∠A+∠B+∠ACB=180°,
∴∠A=180° ∠B ∠ACB=54°,
故答案为:54°.
20.解:(1)在△ABC中,边AB、AC的垂直平分线分别交BC于D、E,
∴DB=DA,EA=EC,
又BC=6,
∴△ADE的周长=AD+DE+EA=BD+DE+EC=BC=6;
(2)∵∠BAC=130°,
∴∠B+∠C=50°,
∵DA=DB,EA=EC,
∴∠BAD=∠B,∠EAC=∠C,
∴∠BAD+∠EAC=50°,
∴∠DAE=∠BAC﹣(∠BAD+∠EAC)=130°﹣50°=80°.
21.解:∵∠BAC=62°,∠B=78°,
∴∠C=180°﹣∠BAC﹣∠B=40°,
∵DE是AC的垂直平分线,
∴DA=DC,
∴∠DAC=∠C=40°,
∴∠BAD=∠BAC﹣∠DAC=22°.
22.解:(1)∵BD是线段AE的垂直平分线,
∴AB=BE,AD=DE,
∵△ABC的周长为18,△DEC的周长为6,
∴AB+BE+EC+CD+AD=18,CD+EC+DE=CD+CE+AD=6,
∴AB+BE=18﹣6=12,
∴AB=6;
(2)∵∠ABC=30°,∠C=45°,
∴∠BAC=180°﹣30°﹣45°=105°,
在△BAD和△BED中,
,
∴△BAD≌△BED(SSS),
∴∠BED=∠BAC=105°,
∴∠CDE=∠BED﹣∠C=105°﹣45°=60°.
23.证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵BE∥AD,
∴∠EBA=∠BAD,∠E=∠CAD,
∴∠EBA=∠E,
∴AE=AB,
又∵F是BE的中点,
∴AF⊥BE.
24.解:(1)∵∠C=90°,∠A=35°,
∴∠ABC=90°﹣∠A=55°,
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠EBA=∠A=35°,
∴∠CBE=∠ABC﹣∠EBA=55°﹣35°=20°;
(2)在Rt△ECB中,∠C=90°,EC=1,BE=AE=3,
由勾股定理得:BC===2,
∵AE=3,EC=1,
∴AC=AE+EC=3+1=4,
∴△ABC的面积是==4.
25.解:∵AC的垂直平分线交AC于点D,
∴EA=EC,
∴∠EAC=∠ECA,
∵∠B=50°,∠BAC=21°,
∴∠ECA=∠B+∠BAC=71°,
∴∠CAE=71°.
26.证明:∵∠BAC=90°,
∴∠ABC+∠C=90°,
∵AM⊥BC,
∴∠AMB=90°,
∴∠ABC+∠BAM=90°,
∴∠C=∠BAM,
∵AD平分∠MAC,
∴∠MAD=∠CAD,
∴∠BAM+∠MAD=∠C+∠CAD,
∵∠ADB=∠C+∠CAD,
∴∠BAD=∠ADB,
∴AB=BD,
∵BE平分∠ABC,
∴BF⊥AD,AF=FD,
即线段BF垂直平分线段AD.
一、选择题
1.如图,△ABC中,AB的垂直平分线DE分别与边AB,AC交于点D,点E,若△ABC与△BCE的周长分别是36cm和22cm,则AD的长是( )
A.7cm B.8cm C.10cm D.14cm
2.如图,△ABC中,∠B=40°,AC的垂直平分线交AC于D,交BC于E,且∠EAB:∠CAE=3:1,则∠C等于( )
A.28° B.25° C.22.5° D.20°
3.如图,△ABC中,∠BAC=130°,AB,AC的垂直平分线分别交BC于点E,F,与AB,AC分别交于点D,G,则∠EAF的度数为( )
A.65° B.60° C.70° D.80°
4.到三角形三个顶点距离都相等的点是( )
A.三角形的三条角平分线的交点
B.三角形的三边垂直平分线的交点
C.三角形的三条高线的交点
D.三角形的三条中线的交点
5.下列条件中,不能判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线的是( )
A.CA=CB,DA=DB B.CA=CB,CD⊥AB
C.CA=DA,CB=DB D.CA=CB,CD平分AB
6.如图,在△ABC中,直线l为边BC的垂直平分线,l交AC于点Q,∠ABC的角平分线与l相交于点P.若∠BAC=60°,∠ACP=24°,则∠PQC是( )
A.34° B.36° C.44° D.46°
7.如图,在Rt△ABC中,ED为AB的垂直平分线,连接CD,若∠B=52°,则∠ACD的度数为( )
A.38° B.48° C.52° D.42°
8.如图,△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,若△ABC周长为16,AC=6,则DC为( )
A.5 B.8 C.9 D.10
9.如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
A.2 B.4 C.6 D.8
10.如图,已知△ABC中,∠B=50°,P为△ABC内一点,过点P的直线MN分别交AB,BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为( )
A.100° B.105° C.115° D.120°
11.如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=6,CF=2,则AC的长度为( )
A.6 B.7 C.8 D.9
12.已知,如图,DE垂直平分AB,交AB于点E,交BC于点D,△ACD的周长是13,BC=8,则AC的长是( )
A.6 B.5 C.4 D.3
13.如图,在△ABC中,线段AB的垂直平分线与AC相交于点D,连接BD,边AC的长为12cm,边BC的长为7cm,则△BCD的周长为( )
A.18cm B.19cm C.20cm D.21cm
14.如图,在△ABC中,∠C=90°,AC=6,BC=8,点P为AC上一点,PA=2,点D在AB上,且∠A=∠PDA,BD的垂直平分线交BC于点E,交BD于点F,连接DE,则线段DE的长为( )
A.4.75 B.5.25 C.6.5 D.7.75
二、填空题
15.如图Rt△ABC中,∠ACB=90°,AC=4,BC=9,ED垂直平分AB,△ACE周长= .
16.如图,△ABC中,D在BC边上,E在AC边上,且DE垂直平分AC.若△ABC的周长为21cm,△ABD的周长为13cm,则AE的长为 .
17.如图,在△ABC中,直线DE垂直平分BC,垂足为E,交AC于点D,若△ABD的周长为12,AB=5,则AC的长为 .
如图,线段AB、BC的垂直平分线l1、l2相交于点O,若∠1=38°,则∠AOC的度数为 .
19.如图,在△ABC中,BC边的垂直平分线交BC于D,交AB于E.若CE平分∠ACB,∠B=42°,则∠A= .
三、解答题
20.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=6,求△ADE的周长;
(2)若∠BAC=130°,求∠DAE的度数.
21.如图,在△ABC中,∠BAC=62°,∠B=78°,AC的垂直平分线交BC于点D,求∠BAD的度数.
22.如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D,连接DE.
(1)若△ABC的周长为18,△DEC的周长为6,求AB的长.
(2)若∠ABC=30°,∠C=45°,求∠CDE的度数.
23.如图,已知AD平分∠BAC,BE∥AD,F是BE的中点,试说明AF⊥BE的理由.
24.如图,Rt△ABC中,∠C=90°,直线DE是边AB的垂直平分线,连接BE.
(1)若∠A=35°,求∠CBE的度数;
(2)若AE=3,EC=1,求△ABC的面积.
25.如图,在△ABC中,AC的垂直平分线交AC于点D,交BC延长线交于点E,连接AE,如果∠B=50°,∠BAC=21°,求∠CAE的度数.
26.如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.求证:线段BF垂直平分线段AD.
参考答案
1.解:∵DE是AB的垂直平分线,
∴EA=EB,AD=BD=AB,
∵△EBC的周长是22cm,
∴BC+BE+EC=22cm,即AC+BC=22cm,
∵△ABC的周长是36cm,
∴AB+AC+BC=36cm,
∴AB=36﹣22=14(cm),
∴AD=AB=×14=7(cm).
故选:A.
2.解:设∠CAE=x,则∠EAB=3x.
∵AC的垂直平分线交AC于D,交BC于E,
∴AE=CE.
∴∠C=∠CAE=x.
根据三角形的内角和定理,得
∠C+∠BAC=180°﹣∠B,
即x+4x=140°,
∴x=28°.
则∠C=28°.
故选:A.
3.解:∵DE垂直平分AB,FG垂直平分AC,
∴EB=EA,FA=FC,
∴∠BAE=∠B,∠FAC=∠C,
∵△ABC中,∠BAC=130°,
∴∠B+∠C=50°,
∴∠BAE+∠FAC=50°,
∴∠EAF=∠BAC﹣(∠BAE+∠FAC)=80°;
故选:D.
4.解:∵到三角形的一边的两端点距离相等的点在这边的垂直平分线上,
∴到三角形三个顶点的距离都相等的点是这个三角形的三条边的垂直平分线的交点,
故选:B.
5.解:A、∵CA=CB,DA=DB,
∴直线CD是线段AB的垂直平分线;
B、∵CA=CB,CD⊥AB,
∴直线CD是线段AB的垂直平分线;
C、当CA=DA,CB=DB时,直线CD不一定是线段AB的垂直平分线;
D、∵CA=CB,CD平分AB,
∴直线CD是线段AB的垂直平分线,
故选:C.
6.解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵直线l是线段BC的垂直平分线,
∴BP=CP,
∴∠CBP=∠BCP,
∴∠ABP=∠BCP,
∵∠A+∠ACB+∠ABC=180°,∠A=60°,∠ACP=24°,
∴3∠ABP+24°+60°=180°,
∴∠ABP=32°,
∴∠PBC=∠PCB=32°,
∴∠PQC=×(180°﹣32°﹣32°)﹣24°=58°﹣24°=34°,
故选:A.
7.解:∵ED为AB的垂直平分线,
∴AD=BD,
∵∠ACB=90°,
∴CD=BD,
∴∠DCB=∠B,
∵∠B=52°,
∴∠DCB=52°,
∴∠ACD=90°﹣52°=38°,
故选:A.
8.解:∵△ABC周长为16,
∴AB+BC+AC=16,
∵AC=6,
∴AB+BC=10,
∵EF垂直平分AC,
∴EA=EC,
∵AB=AE,AD⊥BC,
∴BD=DE,
∴AB+BD=AE+DE=×(AB+BC)=5,
∴DC=DE+EC=AE+DE=5,
故选:A.
9.解:∵DE是AB的垂直平分线,AE=4,
∴EB=EA=4,
∴BC=EB+EC=4+2=6,
故选:C.
10.解:∵∠ABC=50°,
∴∠BAC+∠ACB=130°,
∵M在PA的中垂线上,N在PC的中垂线上,
∴AM=PM,PN=CN,
∴∠MAP=∠APM,∠CPN=∠PCN,
∵∠APC=180°﹣∠APM﹣∠CPN=180°﹣∠PAC﹣∠ACP,
∴∠MAP+∠PCN=∠PAC+∠ACP=×130°=65°,
∴∠APC=115°,
故选:C.
11.解:∵EF是AB的垂直平分线,BF=6,
∴FA=BF=6,
∴AC=FA+CF=6+2=8,
故选:C.
12.解:∵DE垂直平分AB,
∴DA=DB,
∵△ACD的周长是13,
∴AC+DA+CD=13,
∴AC+DB+CD=AC+BC=13,
∵BC=8,
∴AC=5,
故选:B.
13.解:∵线段AB的垂直平分线与AC相交于点D,
∴DA=DB,
∴△BCD的周长=BC+CD+DB=BC+CD+DA=BC+AC,
∵AC=12cm,BC=7cm,
∴△BCD的周长=BC+AC=12+7=19(cm),
故选:B.
14.解:过P点作PG⊥AD交与G点,
∵∠A=∠PDA,
∴G是AD的中点,
∵∠C=90°,AC=6,BC=8,
∴AB=10,
∵AP=2,
∴=,
∴AG=,
∴AD=,
∴BD=10﹣=,
∵BD的垂直平分线交BC,
∴DF=BF,
∴DF=,
∴DE=,
故选:A.
方法2:
解:∵∠C=90°,AC=6,BC=8,
∴AB=10,
∵AP=2,
∴PC=4,设CE=x,则BE=8﹣x,
∵∠A=∠PDA,
∴AP=PD=2,
∵BD的垂直平分线交BC,
∴DE=BE=8﹣x,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠PDA+∠EDF=90°,
∴∠PDE=90°,
在Rt△PEC中,PE2=PC2+CE2,
∴PE2=16+x2,
在Rt△PED中,PE2=PD2+DE2,
∴PE2=4+(8﹣x)2,
∴16+x2=4+(8﹣x)2,
∴x=,
∴DE=8﹣=,
故选:A.
15.解:∵ED垂直平分边AB,
∴EA=EB,
∴△ACE的周长=AC+EC+EA=AC+EC+EB=AC+BC,
∵AC=4,BC=9,
∴△ACE的周长=AC+BC=4+9=13,
故答案为:13.
16.解:∵DE是AC的垂直平分线,
∴DA=DC,AE=EC,
∵△ABC的周长为21cm,
∴AB+BC+AC=21cm,
∵△ABD的周长为13cm,
∴AB+BD+AD=AB+BD+DC=AB+BC=13(cm),
∴AC=8cm,
∴AE=4cm,
故答案为:4cm.
17.解:∵△ABD的周长为12,
∴AB+AD+BD=12,
∵DE垂直平分BC,
∴DB=DC,
∴AB+AD+DC=12,即AB+AC=12,
∵AB=5,
∴AC=7,
故答案为:7.
18.解:连接BO,并延长BO到P,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴AO=OB=OC,∠BDO=∠BEO=90°,
∴∠DOE+∠ABC=180°,
∵∠DOE+∠1=180°,
∴∠ABC=∠1=38°,
∵OA=OB=OC,
∴∠A=∠ABO,∠OBC=∠C,
∵∠AOP=∠A+∠ABO,∠COP=∠C+∠OBC,
∴∠AOC=∠AOP+∠COP=∠A+∠ABC+∠C=2×38°=76°;
故答案为:76°.
19.解:∵E在线段BC的垂直平分线上,
∴BE=CE,
∴∠ECB=∠B=42°,
∵CE平分∠ACB,
∴∠ACD=2∠ECB=84°,
又∵∠A+∠B+∠ACB=180°,
∴∠A=180° ∠B ∠ACB=54°,
故答案为:54°.
20.解:(1)在△ABC中,边AB、AC的垂直平分线分别交BC于D、E,
∴DB=DA,EA=EC,
又BC=6,
∴△ADE的周长=AD+DE+EA=BD+DE+EC=BC=6;
(2)∵∠BAC=130°,
∴∠B+∠C=50°,
∵DA=DB,EA=EC,
∴∠BAD=∠B,∠EAC=∠C,
∴∠BAD+∠EAC=50°,
∴∠DAE=∠BAC﹣(∠BAD+∠EAC)=130°﹣50°=80°.
21.解:∵∠BAC=62°,∠B=78°,
∴∠C=180°﹣∠BAC﹣∠B=40°,
∵DE是AC的垂直平分线,
∴DA=DC,
∴∠DAC=∠C=40°,
∴∠BAD=∠BAC﹣∠DAC=22°.
22.解:(1)∵BD是线段AE的垂直平分线,
∴AB=BE,AD=DE,
∵△ABC的周长为18,△DEC的周长为6,
∴AB+BE+EC+CD+AD=18,CD+EC+DE=CD+CE+AD=6,
∴AB+BE=18﹣6=12,
∴AB=6;
(2)∵∠ABC=30°,∠C=45°,
∴∠BAC=180°﹣30°﹣45°=105°,
在△BAD和△BED中,
,
∴△BAD≌△BED(SSS),
∴∠BED=∠BAC=105°,
∴∠CDE=∠BED﹣∠C=105°﹣45°=60°.
23.证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵BE∥AD,
∴∠EBA=∠BAD,∠E=∠CAD,
∴∠EBA=∠E,
∴AE=AB,
又∵F是BE的中点,
∴AF⊥BE.
24.解:(1)∵∠C=90°,∠A=35°,
∴∠ABC=90°﹣∠A=55°,
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠EBA=∠A=35°,
∴∠CBE=∠ABC﹣∠EBA=55°﹣35°=20°;
(2)在Rt△ECB中,∠C=90°,EC=1,BE=AE=3,
由勾股定理得:BC===2,
∵AE=3,EC=1,
∴AC=AE+EC=3+1=4,
∴△ABC的面积是==4.
25.解:∵AC的垂直平分线交AC于点D,
∴EA=EC,
∴∠EAC=∠ECA,
∵∠B=50°,∠BAC=21°,
∴∠ECA=∠B+∠BAC=71°,
∴∠CAE=71°.
26.证明:∵∠BAC=90°,
∴∠ABC+∠C=90°,
∵AM⊥BC,
∴∠AMB=90°,
∴∠ABC+∠BAM=90°,
∴∠C=∠BAM,
∵AD平分∠MAC,
∴∠MAD=∠CAD,
∴∠BAM+∠MAD=∠C+∠CAD,
∵∠ADB=∠C+∠CAD,
∴∠BAD=∠ADB,
∴AB=BD,
∵BE平分∠ABC,
∴BF⊥AD,AF=FD,
即线段BF垂直平分线段AD.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
