2021-2022学年冀教版八年级数学上册16.2线段的垂直平分线 同步练习题(Word版 含答案)
文档属性
| 名称 | 2021-2022学年冀教版八年级数学上册16.2线段的垂直平分线 同步练习题(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 294.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 21:16:24 | ||
图片预览




文档简介
2021-2022学年冀教版八年级数学上册《16.2线段的垂直平分线》同步练习题(附答案)
一、填空题
1.如图,平面上到两两相交的三条直线a、b、c的距离相等的点一共有 个.
2.已知MN是线段AB的垂直平分线,P、Q是直线MN上两点,且∠PAB=35°,∠QBA=60°,则∠QAP的度数为 .
3.已知C,D两点在线段AB的垂直平分线上,且∠ACB=50°,∠ADB=86°,则∠CAD的度数是 .
4.如图,在△ABC中,点O是BC、AC的垂直平分线的交点,OB=5cm,AB=8cm,则△AOB的周长是 cm.
5.如图,△ABC中,AH为BC边上的高,记S△ABC为S,AH的垂直平分线交边AB于点B1,交边AC于点A1,连接A1B.得到第一个三角形△A1BC,作△A1BC边BC上的高A1H1;作高A1H1的垂直平分线交边AB于点B2,交边AC于点A2,连接A2B,得到第二个三角形△A2BC,作△A2BC边BC上的高A2H2;…依次这样作下去,则第2020个三角形△A2020BC的面积为 .
6.如图,已知A(0,3),B(2,1),C(2,﹣3),若点P是△ABC三边垂直平分线的交点,则点P的坐标为 .
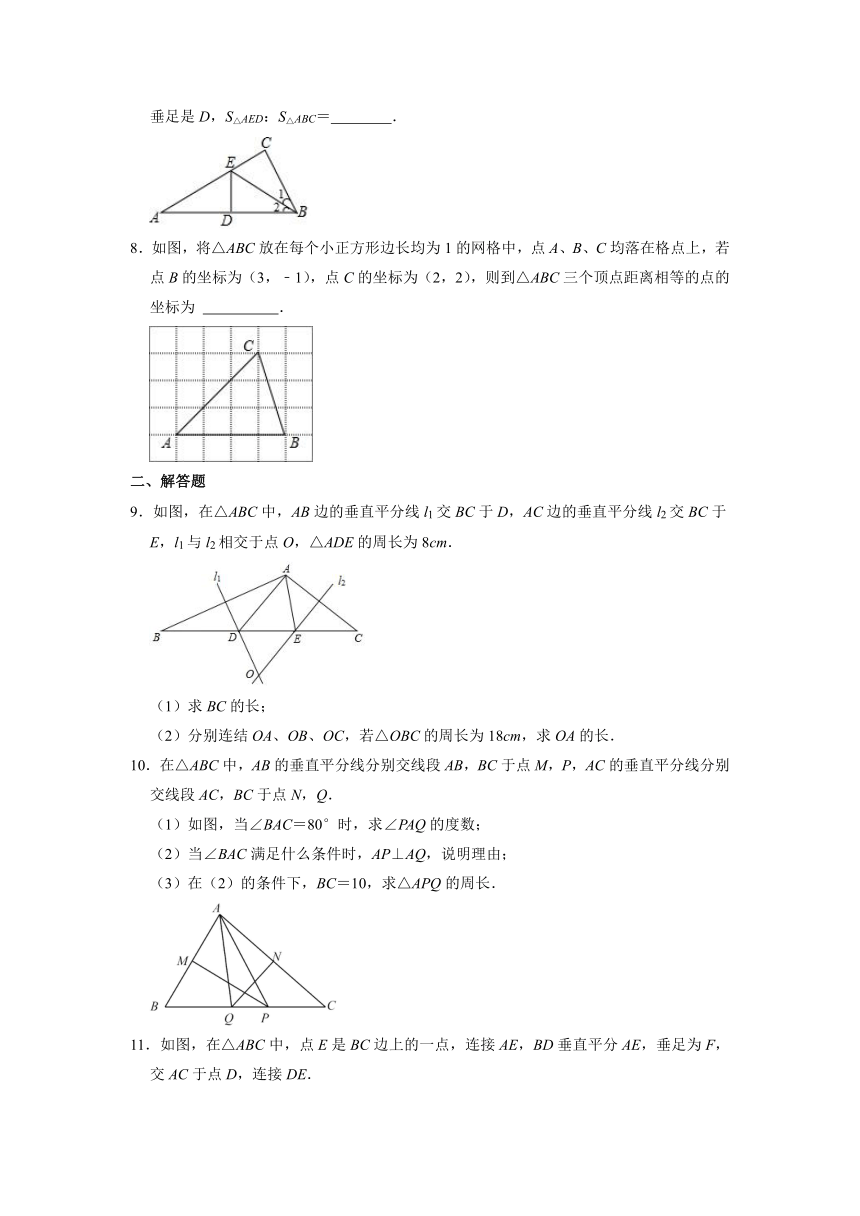
7.如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,S△AED:S△ABC= .
8.如图,将△ABC放在每个小正方形边长均为1的网格中,点A、B、C均落在格点上,若点B的坐标为(3,﹣1),点C的坐标为(2,2),则到△ABC三个顶点距离相等的点的坐标为 .
二、解答题
9.如图,在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,△ADE的周长为8cm.
(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为18cm,求OA的长.
10.在△ABC中,AB的垂直平分线分别交线段AB,BC于点M,P,AC的垂直平分线分别交线段AC,BC于点N,Q.
(1)如图,当∠BAC=80°时,求∠PAQ的度数;
(2)当∠BAC满足什么条件时,AP⊥AQ,说明理由;
(3)在(2)的条件下,BC=10,求△APQ的周长.
11.如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D,连接DE.
(1)若△ABC的周长为18,△DEC的周长为6,求AB的长.
(2)若∠ABC=30°,∠C=45°,求∠CDE的度数.
12.如图,在四边形ABCD中,BD所在的直线垂直平分线段AC,过点A作BC的平行线AF交CD于F,延长AB、DC交于点E.
求证:(1)AC平分∠EAF;
(2)∠FAD=∠E.
13.如图,在△ABC中,DM,EN分别垂直平分边AC和边BC,交边AB于M,N两点,DM与EN相交于点F.
(1)若AB=3cm,求△CMN的周长.
(2)若∠MFN=70°,求∠MCN的度数.
14.如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC.若△ADE的周长为12cm,△OBC的周长为32cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=n°(n>90),直接写出∠DAE的度数 °.
15.已知:△ABC是三边都不相等的三角形,点O和点P是这个三角形内部两点.
(1)如图①,如果点P是这个三角形三个内角平分线的交点,那么∠BPC和∠BAC有怎样的数量关系?请说明理由;
(2)如图②,如果点O是这个三角形三边垂直平分线的交点,那么∠BOC和∠BAC有怎样的数量关系?请说明理由;
(3)如图③,如果点P(三角形三个内角平分线的交点),点O(三角形三边垂直平分线的交点)同时在不等边△ABC的内部,那么∠BPC和∠BOC有怎样的数量关系?请直接回答.
16.已知:如图,AB=AC,DB=DC,点E在AD上,求证:EB=EC.
17.如图,AD与BC相交于点O,OA=OC,∠A=∠C,BE=DE.求证:OE垂直平分BD.
18.如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,AC的垂直平分线BE与CD交于点F,与AC交于点E.
(1)判断△DBC的形状并证明你的结论.
(2)求证:BF=AC.
(3)试说明CE=BF.
19.如图,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,且AB=CD,∠ABD=120°,∠CDB=38°,求∠OBD的度数.
20.如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.求证:DE=EC.(用三种方法证明)
21.如图,Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过点D作AB的垂线交AC于点E,求证:BE垂直平分CD.
参考答案
1.解:如图,
到三条直线a、b、c的距离都相等的点一共有4个.
故答案为:4.
2.解:当点P、Q在AB的同旁时,
∵MN是线段AB的垂直平分线,
∴QA=QB,
∵∠QBA=60°,
∴∠QAB=∠QBA=60°,
∴∠QAP=∠QAB﹣∠PAB=60°﹣35°=25°,
当点P、Q′在AB的两旁时,
∴∠Q′AP=∠Q′AB+∠PAB=60°+35°=95°,
故答案为:25°或95°.
3.解:∵C、D两点在线段AB的中垂线上,
∴CA=CB,DA=DB,
∵CD⊥AB,
∴∠ACD=∠ACB=×50°=25°,∠ADC=∠ADB=×86°=43°,
当点C与点D在线段AB两侧时,∠CAD=180°﹣∠ACD﹣∠ADC=180°﹣25°﹣43°=112°,
当点C与点D′在线段AB同侧时,∠CAD′=∠AD′C﹣∠ACD′=43°﹣25°=18°,
故答案为:18°或112°.
4.解:∵点O是BC、AC的垂直平分线的交点,
∴OA=OB=5cm,
∴△AOB的周长=OA+OB+AB=18(cm),
故答案为:18.
5.解:如图所示,连接A1H,
∵AH的垂直平分线交边AB于点B1,交边AC于点A1,
∴AA1=HA1,
∴∠HAC=∠AHA1,
又∵AH⊥BC,
∴∠HAC+∠C=∠AHA1+∠CHA1=90°,
∴∠C=∠CHA1,
∴HA1=CA1,
∴AA1=CA1,
∴A1是AC的中点,
∴△A1BC的面积=S△ABC=S,
同理可得,A2是A1C的中点,
∴△A2BC的面积=S△A1BC=S,
同理可得,△A3BC的面积=S△A2BC=,
……,
∴第2020个三角形△A2020BC的面积为,
故答案为:.
6.解:如图所示:分别作线段AB、BC的垂直平分线交于点P,
点P的坐标为(﹣2,﹣1),
故答案为:(﹣2,﹣1).
7.解:∵DE垂直平分AB,
∴AD=BD,
∴S△ADE=S△BDE,
∵∠1=∠2,∠C=∠BDE=90°,BE=BE,
∴△BDE≌△BCE(AAS),
∴S△BDE=S△BCE,
∴S△AED:S△ABC=1:3,
故答案为:1:3.
8.解:∵点P到△ABC三个顶点距离相等,
∴点P是边AB、AC的垂直平分线的交点,
如图所示:点P即为所求,此时点P的坐标为(1,0),
故答案为:(1,0).
9.解:(1)在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,
∴AD=BD,AE=CE,
∵△ADE的周长为8cm.
∴BC=BD+DE+CE=AD+DE+AE=8cm;
(2)连接OA、OB、OC,
在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,
∴OA=OB,OA=OC,
∴OA=OB=OC,
∵△OBC的周长为18cm,
∴OB+OC+BC=18cm,
∴OB=OC=5cm,
∴OA=5cm.
10.解:(1)∵MP、NQ分别是AB、AC的垂直平分线,
∴AP=BP,AQ=CQ,
∵∠BAC=80°,
∴∠B+∠C=180°﹣80°=100°,
∵AP=BP,AQ=CQ,
∴∠BAP=∠B,∠CAQ=∠C,
∴∠PAQ=∠BAC﹣∠BAP﹣∠CAQ=∠BAC﹣∠B﹣∠C=100°﹣80°=20°;
(2)如图,
∵AP⊥AQ,
∴∠PAQ=90°,
由(1)得,∠BAP=∠B,∠CAQ=∠C,
∴∠B+∠C=180°﹣∠BAC,∠BAP+∠CAQ=∠BAC﹣90°,
∴180°﹣∠BAC=∠BAC﹣90°,
∴∠BAC=135°;
答:当∠BAC=135°时,AP⊥AQ;
(3)∵△APQ周长=AP+PQ+AQ=BP+PQ+QC=BC,
∵BC=10,
∴△APQ周长=10.
11.解:(1)∵BD是线段AE的垂直平分线,
∴AB=BE,AD=DE,
∵△ABC的周长为18,△DEC的周长为6,
∴AB+BE+EC+CD+AD=18,CD+EC+DE=CD+CE+AD=6,
∴AB+BE=18﹣6=12,
∴AB=6;
(2)∵∠ABC=30°,∠C=45°,
∴∠BAC=180°﹣30°﹣45°=105°,
在△BAD和△BED中,
,
∴△BAD≌△BED(SSS),
∴∠BED=∠BAC=105°,
∴∠CDE=∠BED﹣∠C=105°﹣45°=60°.
12.证明:(1)∵BD所在的直线垂直平分线段AC,
∴BA=BC,
∴∠BAC=∠BCA,
∵BC∥AF,
∴∠CAF=∠BCA,
∴∠CAF=∠BAC,即AC平分∠EAF;
(2)∵BD所在的直线垂直平分线段AC,
∴DA=DC,
∴∠DAC=∠DCA,
∵∠DCA是△ACE的一个外角,
∴∠DCA=∠E+∠EAC,
∴∠E+∠EAC=∠FAD+∠CAF,
∵∠CAF=∠EAC,
∴∠FAD=∠E.
13.解:(1)∵DM、EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB=3(cm);
(2)∵∠MFN=70°,
∴∠MNF+∠NMF=180°﹣70°=110°,
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠MNF+∠NMF=110°,
∴∠A+∠B=90°﹣∠AMD+90°﹣∠BNE=180°﹣110°=70°,
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°﹣2(∠A+∠B)=180°﹣2×70°=40°.
14.解:(1)∵l1是AB边的垂直平分线,
∴DA=DB,
∵l2是AC边的垂直平分线,
∴EA=EC,
BC=BD+DE+EC=DA+DE+EA=12cm;
(2)∵l1是AB边的垂直平分线,
∴OA=OB,
∵l2是AC边的垂直平分线,
∴OA=OC,
∵OB+OC+BC=32cm,
∴OA=OB=OC=10cm;
(3)∵∠BAC=n°,
∴∠ABC+∠ACB=(180﹣n)°,
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∴∠DAE=∠BAC﹣∠BAD﹣∠EAC=n°﹣(180°﹣n°)=2n°﹣180°.
故答案为:(2n﹣180).
15.解:(1)∠BPC=90°+∠BAC
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)
=90°+∠BAC;
(2)∠BOC=2∠BAC
如图,连接AO.
∵点O是这个三角形三边垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,∠OBC=∠OCB,
∴∠AOB=180°﹣2∠OAB,∠AOC=180°﹣2∠OAC,
∴∠BOC=360°﹣(∠AOB+∠AOC)
=360°﹣(180°﹣2∠OAB+180°﹣2∠OAC),
=2∠OAB+2∠OAC
=2∠BAC;
(3)4∠BPC﹣∠BOC=360°,
∵点P为三角形三个内角平分线的交点,
∴∠BPC=90°+∠BAC
由∠BAC=2∠BPC﹣180°
点O为三角形三边垂直平分线的交点
∠BOC=2∠BAC,
∴∠BOC=2(2∠BPC﹣180°)=4∠BPC﹣360°,
即4∠BPC﹣∠BOC=360°.
16.解:∵AB=AC,DB=DC,
∴AD是线段BC的垂直平分线,
∵点E在AD上,
∴EB=EC.
17.证明:在△AOB与△COD中,
,
∴△AOB≌△COD(ASA),
∴OB=OD,
∴点O在线段BD的垂直平分线上,
∵BE=DE,
∴点E在线段BD的垂直平分线上,
∴OE垂直平分BD.
18.解:(1)△DBC是等腰直角三角形,
理由:∵∠ABC=45°,CD⊥AB,
∴∠BCD=45°,
∴BD=CD,
∴△DBC是等腰直角三角形;
(2)∵BE⊥AC,
∴∠BDC=∠BEC=90°,
∵∠BFD=∠CFE,
∴∠DBF=∠ACD,
在△BDF与△CDA中,
,
∴△BDF≌△CDA,
∴BF=AC;
(3)∵BE是AC的垂直平分线,
∴CE=AC,
∴CE=BF.
19.解:连接OA,OC,
∵OE,OF分别是AC,BD的垂直平分线,
∴OA=OC,OB=OD,
∵AB=CD,
∴△ABO≌△CDO(SSS),
∴∠ABO=∠CDO,
设∠OBD=∠ODB=α,∠ABO=∠CDO=β,
∴α+β=120°,β﹣α=38°,
∴α=41°,
∴∠OBD=41°.
20.证明:方法一:如图1,连接BE,
∵DE是AB的垂直平分线,
∴BE=AE,∠ABE=∠A=30°,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∴∠CBE=∠DBE=30°,
∵DE⊥AB,CE⊥BC,
∴CE=DE;
方法二:如图2,连接CD,
∵在△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°,
∵点D是AB的中点,
∴CD=BD=AB,
∴△BDC是等边三角形,
∴∠BCD=∠BDC=60°,
∵∠BDE=∠ACB=90°,
∴∠EDC=∠ECD=30°,
∴DE=CE;
方法三:如图3,延长DE交BC的延长线于F,
∵∠ACB=90°,∠A=30°,
∴∠B=60°,BC=AB,
∵DE垂直平分AB,
∴BD=AD=AB,∠BDF=90°,
∴∠F=30°,
∴BD=BF,
∴CF=BD=AD,
在△ADE与△FCE中,
∴△ADE≌△FCE(AAS),
∴DE=CE.
21.证明:∵∠ACB=90°,DE⊥AB,
∴∠ACB=∠BDE=90°,
在Rt△BDE和Rt△BCE中,
,
∴Rt△BDE≌Rt△BCE,
∴ED=EC,
∵ED=EC,BD=BC,
∴BE垂直平分CD.
一、填空题
1.如图,平面上到两两相交的三条直线a、b、c的距离相等的点一共有 个.
2.已知MN是线段AB的垂直平分线,P、Q是直线MN上两点,且∠PAB=35°,∠QBA=60°,则∠QAP的度数为 .
3.已知C,D两点在线段AB的垂直平分线上,且∠ACB=50°,∠ADB=86°,则∠CAD的度数是 .
4.如图,在△ABC中,点O是BC、AC的垂直平分线的交点,OB=5cm,AB=8cm,则△AOB的周长是 cm.
5.如图,△ABC中,AH为BC边上的高,记S△ABC为S,AH的垂直平分线交边AB于点B1,交边AC于点A1,连接A1B.得到第一个三角形△A1BC,作△A1BC边BC上的高A1H1;作高A1H1的垂直平分线交边AB于点B2,交边AC于点A2,连接A2B,得到第二个三角形△A2BC,作△A2BC边BC上的高A2H2;…依次这样作下去,则第2020个三角形△A2020BC的面积为 .
6.如图,已知A(0,3),B(2,1),C(2,﹣3),若点P是△ABC三边垂直平分线的交点,则点P的坐标为 .
7.如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,S△AED:S△ABC= .
8.如图,将△ABC放在每个小正方形边长均为1的网格中,点A、B、C均落在格点上,若点B的坐标为(3,﹣1),点C的坐标为(2,2),则到△ABC三个顶点距离相等的点的坐标为 .
二、解答题
9.如图,在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,△ADE的周长为8cm.
(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为18cm,求OA的长.
10.在△ABC中,AB的垂直平分线分别交线段AB,BC于点M,P,AC的垂直平分线分别交线段AC,BC于点N,Q.
(1)如图,当∠BAC=80°时,求∠PAQ的度数;
(2)当∠BAC满足什么条件时,AP⊥AQ,说明理由;
(3)在(2)的条件下,BC=10,求△APQ的周长.
11.如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D,连接DE.
(1)若△ABC的周长为18,△DEC的周长为6,求AB的长.
(2)若∠ABC=30°,∠C=45°,求∠CDE的度数.
12.如图,在四边形ABCD中,BD所在的直线垂直平分线段AC,过点A作BC的平行线AF交CD于F,延长AB、DC交于点E.
求证:(1)AC平分∠EAF;
(2)∠FAD=∠E.
13.如图,在△ABC中,DM,EN分别垂直平分边AC和边BC,交边AB于M,N两点,DM与EN相交于点F.
(1)若AB=3cm,求△CMN的周长.
(2)若∠MFN=70°,求∠MCN的度数.
14.如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC.若△ADE的周长为12cm,△OBC的周长为32cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=n°(n>90),直接写出∠DAE的度数 °.
15.已知:△ABC是三边都不相等的三角形,点O和点P是这个三角形内部两点.
(1)如图①,如果点P是这个三角形三个内角平分线的交点,那么∠BPC和∠BAC有怎样的数量关系?请说明理由;
(2)如图②,如果点O是这个三角形三边垂直平分线的交点,那么∠BOC和∠BAC有怎样的数量关系?请说明理由;
(3)如图③,如果点P(三角形三个内角平分线的交点),点O(三角形三边垂直平分线的交点)同时在不等边△ABC的内部,那么∠BPC和∠BOC有怎样的数量关系?请直接回答.
16.已知:如图,AB=AC,DB=DC,点E在AD上,求证:EB=EC.
17.如图,AD与BC相交于点O,OA=OC,∠A=∠C,BE=DE.求证:OE垂直平分BD.
18.如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,AC的垂直平分线BE与CD交于点F,与AC交于点E.
(1)判断△DBC的形状并证明你的结论.
(2)求证:BF=AC.
(3)试说明CE=BF.
19.如图,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,且AB=CD,∠ABD=120°,∠CDB=38°,求∠OBD的度数.
20.如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.求证:DE=EC.(用三种方法证明)
21.如图,Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过点D作AB的垂线交AC于点E,求证:BE垂直平分CD.
参考答案
1.解:如图,
到三条直线a、b、c的距离都相等的点一共有4个.
故答案为:4.
2.解:当点P、Q在AB的同旁时,
∵MN是线段AB的垂直平分线,
∴QA=QB,
∵∠QBA=60°,
∴∠QAB=∠QBA=60°,
∴∠QAP=∠QAB﹣∠PAB=60°﹣35°=25°,
当点P、Q′在AB的两旁时,
∴∠Q′AP=∠Q′AB+∠PAB=60°+35°=95°,
故答案为:25°或95°.
3.解:∵C、D两点在线段AB的中垂线上,
∴CA=CB,DA=DB,
∵CD⊥AB,
∴∠ACD=∠ACB=×50°=25°,∠ADC=∠ADB=×86°=43°,
当点C与点D在线段AB两侧时,∠CAD=180°﹣∠ACD﹣∠ADC=180°﹣25°﹣43°=112°,
当点C与点D′在线段AB同侧时,∠CAD′=∠AD′C﹣∠ACD′=43°﹣25°=18°,
故答案为:18°或112°.
4.解:∵点O是BC、AC的垂直平分线的交点,
∴OA=OB=5cm,
∴△AOB的周长=OA+OB+AB=18(cm),
故答案为:18.
5.解:如图所示,连接A1H,
∵AH的垂直平分线交边AB于点B1,交边AC于点A1,
∴AA1=HA1,
∴∠HAC=∠AHA1,
又∵AH⊥BC,
∴∠HAC+∠C=∠AHA1+∠CHA1=90°,
∴∠C=∠CHA1,
∴HA1=CA1,
∴AA1=CA1,
∴A1是AC的中点,
∴△A1BC的面积=S△ABC=S,
同理可得,A2是A1C的中点,
∴△A2BC的面积=S△A1BC=S,
同理可得,△A3BC的面积=S△A2BC=,
……,
∴第2020个三角形△A2020BC的面积为,
故答案为:.
6.解:如图所示:分别作线段AB、BC的垂直平分线交于点P,
点P的坐标为(﹣2,﹣1),
故答案为:(﹣2,﹣1).
7.解:∵DE垂直平分AB,
∴AD=BD,
∴S△ADE=S△BDE,
∵∠1=∠2,∠C=∠BDE=90°,BE=BE,
∴△BDE≌△BCE(AAS),
∴S△BDE=S△BCE,
∴S△AED:S△ABC=1:3,
故答案为:1:3.
8.解:∵点P到△ABC三个顶点距离相等,
∴点P是边AB、AC的垂直平分线的交点,
如图所示:点P即为所求,此时点P的坐标为(1,0),
故答案为:(1,0).
9.解:(1)在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,
∴AD=BD,AE=CE,
∵△ADE的周长为8cm.
∴BC=BD+DE+CE=AD+DE+AE=8cm;
(2)连接OA、OB、OC,
在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O,
∴OA=OB,OA=OC,
∴OA=OB=OC,
∵△OBC的周长为18cm,
∴OB+OC+BC=18cm,
∴OB=OC=5cm,
∴OA=5cm.
10.解:(1)∵MP、NQ分别是AB、AC的垂直平分线,
∴AP=BP,AQ=CQ,
∵∠BAC=80°,
∴∠B+∠C=180°﹣80°=100°,
∵AP=BP,AQ=CQ,
∴∠BAP=∠B,∠CAQ=∠C,
∴∠PAQ=∠BAC﹣∠BAP﹣∠CAQ=∠BAC﹣∠B﹣∠C=100°﹣80°=20°;
(2)如图,
∵AP⊥AQ,
∴∠PAQ=90°,
由(1)得,∠BAP=∠B,∠CAQ=∠C,
∴∠B+∠C=180°﹣∠BAC,∠BAP+∠CAQ=∠BAC﹣90°,
∴180°﹣∠BAC=∠BAC﹣90°,
∴∠BAC=135°;
答:当∠BAC=135°时,AP⊥AQ;
(3)∵△APQ周长=AP+PQ+AQ=BP+PQ+QC=BC,
∵BC=10,
∴△APQ周长=10.
11.解:(1)∵BD是线段AE的垂直平分线,
∴AB=BE,AD=DE,
∵△ABC的周长为18,△DEC的周长为6,
∴AB+BE+EC+CD+AD=18,CD+EC+DE=CD+CE+AD=6,
∴AB+BE=18﹣6=12,
∴AB=6;
(2)∵∠ABC=30°,∠C=45°,
∴∠BAC=180°﹣30°﹣45°=105°,
在△BAD和△BED中,
,
∴△BAD≌△BED(SSS),
∴∠BED=∠BAC=105°,
∴∠CDE=∠BED﹣∠C=105°﹣45°=60°.
12.证明:(1)∵BD所在的直线垂直平分线段AC,
∴BA=BC,
∴∠BAC=∠BCA,
∵BC∥AF,
∴∠CAF=∠BCA,
∴∠CAF=∠BAC,即AC平分∠EAF;
(2)∵BD所在的直线垂直平分线段AC,
∴DA=DC,
∴∠DAC=∠DCA,
∵∠DCA是△ACE的一个外角,
∴∠DCA=∠E+∠EAC,
∴∠E+∠EAC=∠FAD+∠CAF,
∵∠CAF=∠EAC,
∴∠FAD=∠E.
13.解:(1)∵DM、EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB=3(cm);
(2)∵∠MFN=70°,
∴∠MNF+∠NMF=180°﹣70°=110°,
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠MNF+∠NMF=110°,
∴∠A+∠B=90°﹣∠AMD+90°﹣∠BNE=180°﹣110°=70°,
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°﹣2(∠A+∠B)=180°﹣2×70°=40°.
14.解:(1)∵l1是AB边的垂直平分线,
∴DA=DB,
∵l2是AC边的垂直平分线,
∴EA=EC,
BC=BD+DE+EC=DA+DE+EA=12cm;
(2)∵l1是AB边的垂直平分线,
∴OA=OB,
∵l2是AC边的垂直平分线,
∴OA=OC,
∵OB+OC+BC=32cm,
∴OA=OB=OC=10cm;
(3)∵∠BAC=n°,
∴∠ABC+∠ACB=(180﹣n)°,
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∴∠DAE=∠BAC﹣∠BAD﹣∠EAC=n°﹣(180°﹣n°)=2n°﹣180°.
故答案为:(2n﹣180).
15.解:(1)∠BPC=90°+∠BAC
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)
=90°+∠BAC;
(2)∠BOC=2∠BAC
如图,连接AO.
∵点O是这个三角形三边垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,∠OBC=∠OCB,
∴∠AOB=180°﹣2∠OAB,∠AOC=180°﹣2∠OAC,
∴∠BOC=360°﹣(∠AOB+∠AOC)
=360°﹣(180°﹣2∠OAB+180°﹣2∠OAC),
=2∠OAB+2∠OAC
=2∠BAC;
(3)4∠BPC﹣∠BOC=360°,
∵点P为三角形三个内角平分线的交点,
∴∠BPC=90°+∠BAC
由∠BAC=2∠BPC﹣180°
点O为三角形三边垂直平分线的交点
∠BOC=2∠BAC,
∴∠BOC=2(2∠BPC﹣180°)=4∠BPC﹣360°,
即4∠BPC﹣∠BOC=360°.
16.解:∵AB=AC,DB=DC,
∴AD是线段BC的垂直平分线,
∵点E在AD上,
∴EB=EC.
17.证明:在△AOB与△COD中,
,
∴△AOB≌△COD(ASA),
∴OB=OD,
∴点O在线段BD的垂直平分线上,
∵BE=DE,
∴点E在线段BD的垂直平分线上,
∴OE垂直平分BD.
18.解:(1)△DBC是等腰直角三角形,
理由:∵∠ABC=45°,CD⊥AB,
∴∠BCD=45°,
∴BD=CD,
∴△DBC是等腰直角三角形;
(2)∵BE⊥AC,
∴∠BDC=∠BEC=90°,
∵∠BFD=∠CFE,
∴∠DBF=∠ACD,
在△BDF与△CDA中,
,
∴△BDF≌△CDA,
∴BF=AC;
(3)∵BE是AC的垂直平分线,
∴CE=AC,
∴CE=BF.
19.解:连接OA,OC,
∵OE,OF分别是AC,BD的垂直平分线,
∴OA=OC,OB=OD,
∵AB=CD,
∴△ABO≌△CDO(SSS),
∴∠ABO=∠CDO,
设∠OBD=∠ODB=α,∠ABO=∠CDO=β,
∴α+β=120°,β﹣α=38°,
∴α=41°,
∴∠OBD=41°.
20.证明:方法一:如图1,连接BE,
∵DE是AB的垂直平分线,
∴BE=AE,∠ABE=∠A=30°,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∴∠CBE=∠DBE=30°,
∵DE⊥AB,CE⊥BC,
∴CE=DE;
方法二:如图2,连接CD,
∵在△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°,
∵点D是AB的中点,
∴CD=BD=AB,
∴△BDC是等边三角形,
∴∠BCD=∠BDC=60°,
∵∠BDE=∠ACB=90°,
∴∠EDC=∠ECD=30°,
∴DE=CE;
方法三:如图3,延长DE交BC的延长线于F,
∵∠ACB=90°,∠A=30°,
∴∠B=60°,BC=AB,
∵DE垂直平分AB,
∴BD=AD=AB,∠BDF=90°,
∴∠F=30°,
∴BD=BF,
∴CF=BD=AD,
在△ADE与△FCE中,
∴△ADE≌△FCE(AAS),
∴DE=CE.
21.证明:∵∠ACB=90°,DE⊥AB,
∴∠ACB=∠BDE=90°,
在Rt△BDE和Rt△BCE中,
,
∴Rt△BDE≌Rt△BCE,
∴ED=EC,
∵ED=EC,BD=BC,
∴BE垂直平分CD.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
