第二十四章 圆单元质量检测试卷A(含答案)
文档属性
| 名称 | 第二十四章 圆单元质量检测试卷A(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 11:47:49 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2021-20202年九年级(上)第二十四章圆检测试卷A
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
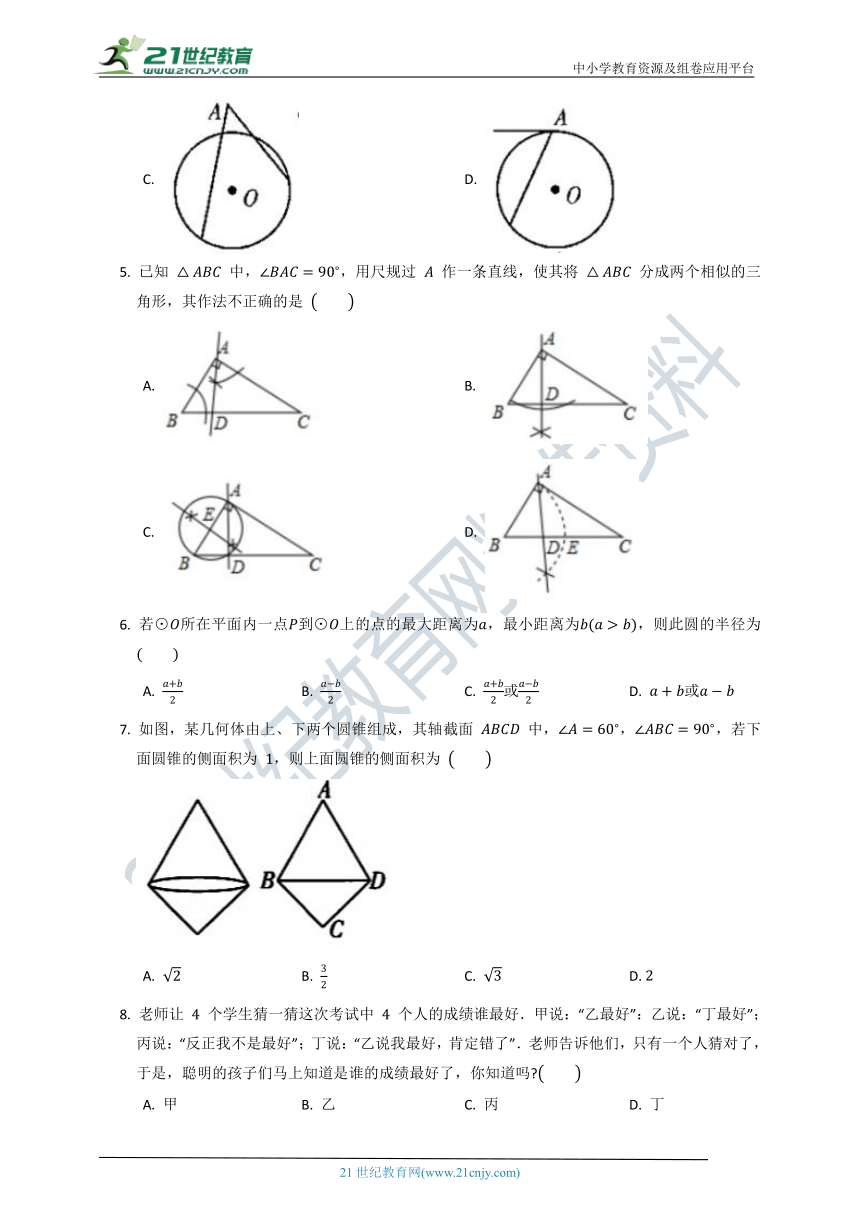
1. 小明用如图所示的扇形纸片折叠成一个圆锥的侧面,已知圆锥的母线长为 ,扇形的弧长是 ,那么这个圆锥的高是
A. B. C. D.
2. 如图, 为 的直径,点 , 在 上.若 ,则 的度数为
A. B. C. D.
3. 给出下列四个结论,其中正确的结论为
A. 菱形的四个顶点在同一个圆上
B. 正多边形都是轴对称图形
C. 正多边形都是中心对称图形
D. 各角相等的圆内接多边形是正多边形
4. 下列各圆中, 是圆周角的是
A. B.
C. D.
5. 已知 中,,用尺规过 作一条直线,使其将 分成两个相似的三角形,其作法不正确的是
A. B.
C. D.
6. 若⊙所在平面内一点到⊙上的点的最大距离为,最小距离为,则此圆的半径为
A. B. C. 或 D. 或
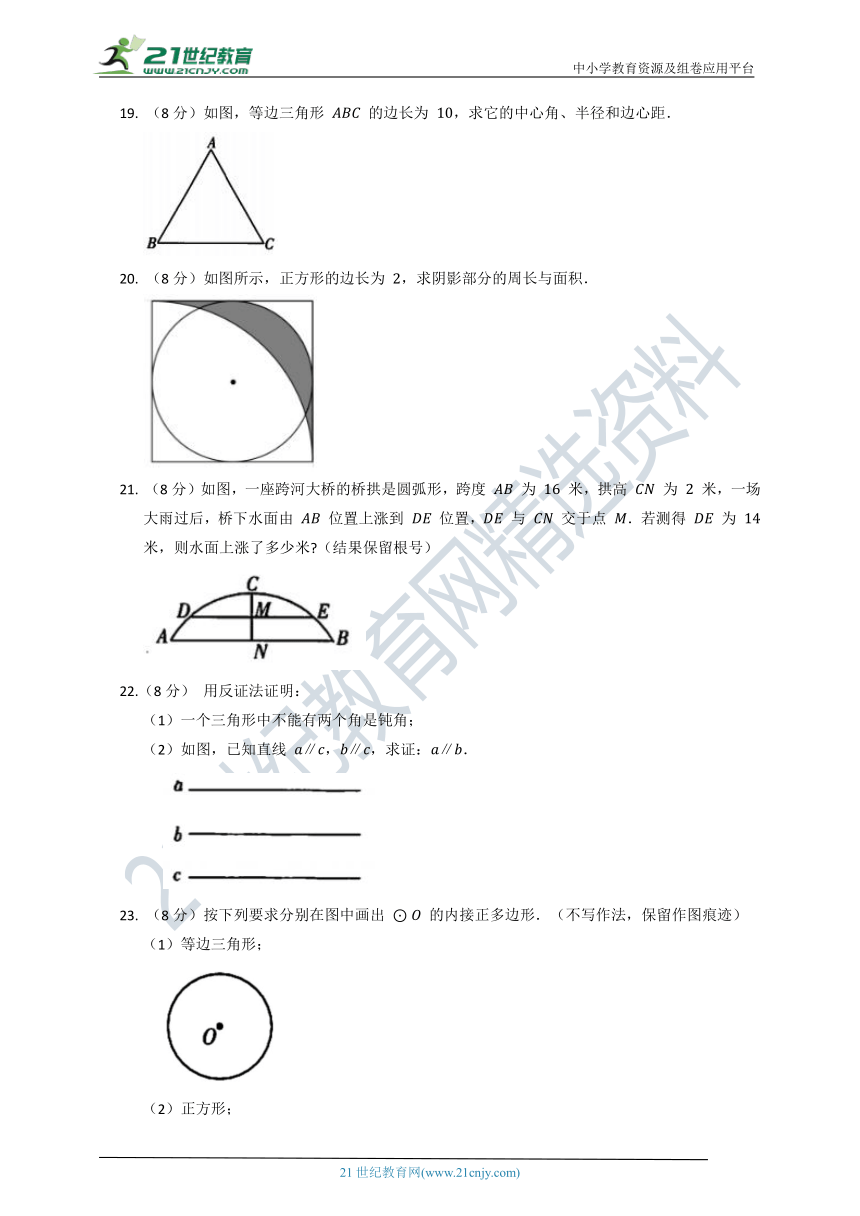
7. 如图,某几何体由上、下两个圆锥组成,其轴截面 中,,,若下面圆锥的侧面积为 ,则上面圆锥的侧面积为
A. B. C. D.
8. 老师让 个学生猜一猜这次考试中 个人的成绩谁最好.甲说:“乙最好”:乙说:“丁最好”;丙说:“反正我不是最好”;丁说:“乙说我最好,肯定错了”.老师告诉他们,只有一个人猜对了,于是,聪明的孩子们马上知道是谁的成绩最好了,你知道吗
A. 甲 B. 乙 C. 丙 D. 丁
9. 如图,在 中,,,, 是 的外接圆,则下列说法正确的个数是
① 和 都是劣弧;
② 是 中最长的弦;
③ ,, 三点能确定一个圆;
④ 的半径为 .
A. B. C. D.
10. 如图所示,在 中,,,,点 , 分别是边 , 上的动点,连接 ,过点 作 交 于点 ,垂足为 ,连接 ,则 的最小值是
A. B. C. D.
二、填空题(共6小题;每小题3分,共18分)
11. 的半径为 ,点 到直线 的距离为 ,当 时, 与 相切.
12. 若两圆的半径分别是 和 ,且两圆的位置关系是相切,则圆心距为 .
13. , 是半径为 的 上不重合的两个点,则线段 的取值范围是 .
14. 如图, 是 的切线, 是 的割线,如果 ,,那么 的长为 .
15. 已知 的半径为 ,直线 与 有公共点,则圆心到直线 的距离 的取值范围是 .
16. 如图, 是 的外接圆,连接 并延长交 于点 ,若 ,则 的度数为 .
三、解答题(共9小题;共72分)
17. (8分)如图,已知 内接于 , 为 的直径,点 在劣弧 上(不与点 , 重合),设 ,,小明同学通过画图和测量得到以下近似数据:
试判断 与 之间的关系,并给出证明.
18. (8分)如图,已知等边三角形 ,边长 ,
(1)作 的外接圆;
(2)求 的度数;
(3)求外接圆的半径.
19. (8分)如图,等边三角形 的边长为 ,求它的中心角、半径和边心距.
20. (8分)如图所示,正方形的边长为 ,求阴影部分的周长与面积.
21. (8分)如图,一座跨河大桥的桥拱是圆弧形,跨度 为 米,拱高 为 米,一场大雨过后,桥下水面由 位置上涨到 位置, 与 交于点 .若测得 为 米,则水面上涨了多少米 (结果保留根号)
22.(8分) 用反证法证明:
(1)一个三角形中不能有两个角是钝角;
(2)如图,已知直线 ,,求证:.
23. (8分)按下列要求分别在图中画出 的内接正多边形.(不写作法,保留作图痕迹)
(1)等边三角形;
(2)正方形;
(3)正六边形;
(4)正八边形.
24. (8分)如图, 是 的外接圆, 平分 的外角 ,,,垂足分别是点 ,,且 .求证:
(1);
(2).
25. (8分)若一个圆锥的高为 ,侧面展开图是一个半圆.求:
(1)圆锥的母线长与底面半径的比;
(2)圆锥的全面积.
答案
第一部分
1. A
2. B
3. B
4. A
5. D
【解析】A、由作图可知:,可以推出 ,故 与 相似,故本选项不符合题意;
B、由作图可知:,
,故 ,故本选项不符合题意;
C、由作图可知:,
,故 ,故本选项不符合题意;
D、无法判断 ,故本选项符合题意.
6. C 【解析】【分析】搞清⊙所在平面内一点到⊙上的点的最大距离、最小距离的差或和为⊙的直径,即可求解.
【解析】解:若⊙所在平面内一点到⊙上的点的最大距离为,最小距离为,若这个点在圆的内部或在圆上时时,圆的直径是,因而半径是;当此点在圆外时,圆的直径是,因而半径是.则此圆的半径为或.
故选:.
【点评】注意到分两种情况进行讨论是解决本题的关键.
7. C
8. C 【解析】假设甲最好,则甲说得错了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是甲最好;
假设乙最好,则甲说对了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是乙最好;
假设丙最好,则甲说错了,则乙说错了,丙说错了,丁说对了,与老师说的“只有一个人猜对了,”不矛盾,因此是丙最好;
假设丁最好,则甲说错了,则乙说对了,丙说对了,丁说错了,与老师说的“只有一个人猜对了,”矛盾,因此是丁不是最好;
因此丙的成绩最好.
9. C 【解析】① 和 都用两个字母表示,是小于半圆的弧,是劣弧,故①正确;
②因为 ,所以 是 的直径,又直径是圆中最长的弦,故②正确;
③过同一条直线上的三个点不能作圆,故③错误;
④因为 ,,,
所以 ,
所以 的半径为 ,故④正确.
故选C.
10. C
【解析】如图所示,延长 到点 ,使 ,连接 ,过点 作 于点 ,取 中点 ,连接 ,过点 作 于点 ,
,,,
,,
是等边三角形,
.
中,,
当 ,, 在同一直线上时, 取得最小值.
于点 ,
.
为 的中点,
,
,, 三点共圆,圆心为 ,即点 在 上运动,
当点 运动到 上时, 取得最小值.
中,,,,
,
的最小值为 .
第二部分
11.
12. 或
13.
14.
15.
16.
【解析】连接 ,如图.
因为 为直径,
所以 ,
因为 与 所对的弧为 ,
所以 ,
所以 .
第三部分
17. .
证明:如答图,连接 .
为 的直径,
.
,
.
,,, 四点共圆,
.
,
.
.
18. (1) 如图所示:
(2) 是等边三角形.
.
.
.
(3) , 即为 的半径.
,
.
.
,解得 .
19. 如图,
设等边三角形 的中心为点 ,过点 作 于点 ,连接 ,,则 ,,.
.
.
设 ,则 .
在 中,,
即 .
解得 (负值已舍去).
,.
等边三角形 的中心角为 ,半径为 ,边心距为 .
20. ();
,
,
.
(),
,
,
,
.
21. 如图,延长 至点 ,使得 ,则点 即为圆心,连接 .
由题意,得 ,
.
同理可得 .
设圆弧形拱桥所在圆的半径为 米,
则 米.
在 中,,
即 .
解得 .
在 中,,
.
.
答:水面上涨了 米.
22. (1) 假设 中,, 为钝角,
,
这与三角形内角和定理相矛盾,
故假设不成立,故原命题正确.
(2) 假设 与 相交于 ,
则过 点有两条直线平行于直线 ,
这与过直线外一点平行于已知直线的直线有且只有一条相矛盾,
所以 .
23. (1) 如图,正多边形即为所求.
(2)
(3)
(4)
24. (1) 平分 ,
,
,
,,
,
.
,,
,,
.
,,
,
;
(2) ,,,
是 的平分线,
,
平分 ,
,
,
.
25. (1) 设圆锥的母线长为 ,底面圆的半径为 ,根据题意得 ,
,即圆锥的母线长与底面半径的比为 .
(2) ,即 ,
,
,
圆锥的全面积 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版2021-20202年九年级(上)第二十四章圆检测试卷A
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 小明用如图所示的扇形纸片折叠成一个圆锥的侧面,已知圆锥的母线长为 ,扇形的弧长是 ,那么这个圆锥的高是
A. B. C. D.
2. 如图, 为 的直径,点 , 在 上.若 ,则 的度数为
A. B. C. D.
3. 给出下列四个结论,其中正确的结论为
A. 菱形的四个顶点在同一个圆上
B. 正多边形都是轴对称图形
C. 正多边形都是中心对称图形
D. 各角相等的圆内接多边形是正多边形
4. 下列各圆中, 是圆周角的是
A. B.
C. D.
5. 已知 中,,用尺规过 作一条直线,使其将 分成两个相似的三角形,其作法不正确的是
A. B.
C. D.
6. 若⊙所在平面内一点到⊙上的点的最大距离为,最小距离为,则此圆的半径为
A. B. C. 或 D. 或
7. 如图,某几何体由上、下两个圆锥组成,其轴截面 中,,,若下面圆锥的侧面积为 ,则上面圆锥的侧面积为
A. B. C. D.
8. 老师让 个学生猜一猜这次考试中 个人的成绩谁最好.甲说:“乙最好”:乙说:“丁最好”;丙说:“反正我不是最好”;丁说:“乙说我最好,肯定错了”.老师告诉他们,只有一个人猜对了,于是,聪明的孩子们马上知道是谁的成绩最好了,你知道吗
A. 甲 B. 乙 C. 丙 D. 丁
9. 如图,在 中,,,, 是 的外接圆,则下列说法正确的个数是
① 和 都是劣弧;
② 是 中最长的弦;
③ ,, 三点能确定一个圆;
④ 的半径为 .
A. B. C. D.
10. 如图所示,在 中,,,,点 , 分别是边 , 上的动点,连接 ,过点 作 交 于点 ,垂足为 ,连接 ,则 的最小值是
A. B. C. D.
二、填空题(共6小题;每小题3分,共18分)
11. 的半径为 ,点 到直线 的距离为 ,当 时, 与 相切.
12. 若两圆的半径分别是 和 ,且两圆的位置关系是相切,则圆心距为 .
13. , 是半径为 的 上不重合的两个点,则线段 的取值范围是 .
14. 如图, 是 的切线, 是 的割线,如果 ,,那么 的长为 .
15. 已知 的半径为 ,直线 与 有公共点,则圆心到直线 的距离 的取值范围是 .
16. 如图, 是 的外接圆,连接 并延长交 于点 ,若 ,则 的度数为 .
三、解答题(共9小题;共72分)
17. (8分)如图,已知 内接于 , 为 的直径,点 在劣弧 上(不与点 , 重合),设 ,,小明同学通过画图和测量得到以下近似数据:
试判断 与 之间的关系,并给出证明.
18. (8分)如图,已知等边三角形 ,边长 ,
(1)作 的外接圆;
(2)求 的度数;
(3)求外接圆的半径.
19. (8分)如图,等边三角形 的边长为 ,求它的中心角、半径和边心距.
20. (8分)如图所示,正方形的边长为 ,求阴影部分的周长与面积.
21. (8分)如图,一座跨河大桥的桥拱是圆弧形,跨度 为 米,拱高 为 米,一场大雨过后,桥下水面由 位置上涨到 位置, 与 交于点 .若测得 为 米,则水面上涨了多少米 (结果保留根号)
22.(8分) 用反证法证明:
(1)一个三角形中不能有两个角是钝角;
(2)如图,已知直线 ,,求证:.
23. (8分)按下列要求分别在图中画出 的内接正多边形.(不写作法,保留作图痕迹)
(1)等边三角形;
(2)正方形;
(3)正六边形;
(4)正八边形.
24. (8分)如图, 是 的外接圆, 平分 的外角 ,,,垂足分别是点 ,,且 .求证:
(1);
(2).
25. (8分)若一个圆锥的高为 ,侧面展开图是一个半圆.求:
(1)圆锥的母线长与底面半径的比;
(2)圆锥的全面积.
答案
第一部分
1. A
2. B
3. B
4. A
5. D
【解析】A、由作图可知:,可以推出 ,故 与 相似,故本选项不符合题意;
B、由作图可知:,
,故 ,故本选项不符合题意;
C、由作图可知:,
,故 ,故本选项不符合题意;
D、无法判断 ,故本选项符合题意.
6. C 【解析】【分析】搞清⊙所在平面内一点到⊙上的点的最大距离、最小距离的差或和为⊙的直径,即可求解.
【解析】解:若⊙所在平面内一点到⊙上的点的最大距离为,最小距离为,若这个点在圆的内部或在圆上时时,圆的直径是,因而半径是;当此点在圆外时,圆的直径是,因而半径是.则此圆的半径为或.
故选:.
【点评】注意到分两种情况进行讨论是解决本题的关键.
7. C
8. C 【解析】假设甲最好,则甲说得错了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是甲最好;
假设乙最好,则甲说对了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是乙最好;
假设丙最好,则甲说错了,则乙说错了,丙说错了,丁说对了,与老师说的“只有一个人猜对了,”不矛盾,因此是丙最好;
假设丁最好,则甲说错了,则乙说对了,丙说对了,丁说错了,与老师说的“只有一个人猜对了,”矛盾,因此是丁不是最好;
因此丙的成绩最好.
9. C 【解析】① 和 都用两个字母表示,是小于半圆的弧,是劣弧,故①正确;
②因为 ,所以 是 的直径,又直径是圆中最长的弦,故②正确;
③过同一条直线上的三个点不能作圆,故③错误;
④因为 ,,,
所以 ,
所以 的半径为 ,故④正确.
故选C.
10. C
【解析】如图所示,延长 到点 ,使 ,连接 ,过点 作 于点 ,取 中点 ,连接 ,过点 作 于点 ,
,,,
,,
是等边三角形,
.
中,,
当 ,, 在同一直线上时, 取得最小值.
于点 ,
.
为 的中点,
,
,, 三点共圆,圆心为 ,即点 在 上运动,
当点 运动到 上时, 取得最小值.
中,,,,
,
的最小值为 .
第二部分
11.
12. 或
13.
14.
15.
16.
【解析】连接 ,如图.
因为 为直径,
所以 ,
因为 与 所对的弧为 ,
所以 ,
所以 .
第三部分
17. .
证明:如答图,连接 .
为 的直径,
.
,
.
,,, 四点共圆,
.
,
.
.
18. (1) 如图所示:
(2) 是等边三角形.
.
.
.
(3) , 即为 的半径.
,
.
.
,解得 .
19. 如图,
设等边三角形 的中心为点 ,过点 作 于点 ,连接 ,,则 ,,.
.
.
设 ,则 .
在 中,,
即 .
解得 (负值已舍去).
,.
等边三角形 的中心角为 ,半径为 ,边心距为 .
20. ();
,
,
.
(),
,
,
,
.
21. 如图,延长 至点 ,使得 ,则点 即为圆心,连接 .
由题意,得 ,
.
同理可得 .
设圆弧形拱桥所在圆的半径为 米,
则 米.
在 中,,
即 .
解得 .
在 中,,
.
.
答:水面上涨了 米.
22. (1) 假设 中,, 为钝角,
,
这与三角形内角和定理相矛盾,
故假设不成立,故原命题正确.
(2) 假设 与 相交于 ,
则过 点有两条直线平行于直线 ,
这与过直线外一点平行于已知直线的直线有且只有一条相矛盾,
所以 .
23. (1) 如图,正多边形即为所求.
(2)
(3)
(4)
24. (1) 平分 ,
,
,
,,
,
.
,,
,,
.
,,
,
;
(2) ,,,
是 的平分线,
,
平分 ,
,
,
.
25. (1) 设圆锥的母线长为 ,底面圆的半径为 ,根据题意得 ,
,即圆锥的母线长与底面半径的比为 .
(2) ,即 ,
,
,
圆锥的全面积 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
