2021-2022学年第一学期人教版八年级数学上册11.1.2三角形高、中线与角平分线课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年第一学期人教版八年级数学上册11.1.2三角形高、中线与角平分线课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 12:38:49 | ||
图片预览


文档简介
(共18张PPT)
11.1.2三角形的高.中线与角平分线
2.线段中点的定义
1.角平分线的定义
3.垂线的定义
复习
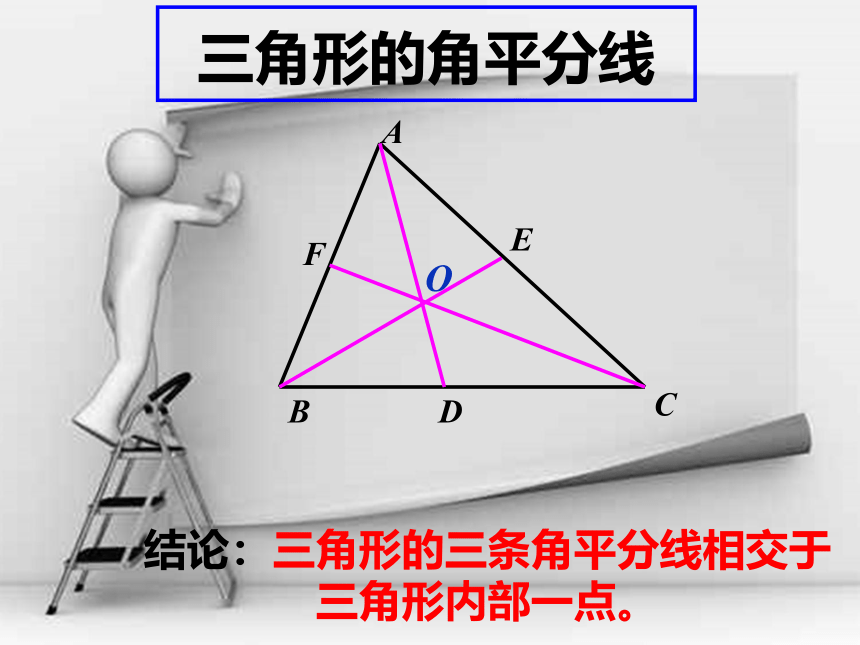
三角形的角平分线
叫做三角形的角平分线。
A
B
C
D
∵AD是 △ ABC的角平分线
∴∠ 1 = ∠2
●
●
在三角形中,一个
角的角平分线与它的对边相交,
这个角的顶点与交点之间的线段,
︶
︶
1
2
几何语言:
∴∠ BAC = 2∠1= 2∠2
∴∠ 1 = 2=
∠ BAC
A
C
B
F
E
D
O
三角形的角平分线
结论:三角形的三条角平分线相交于
三角形内部一点。
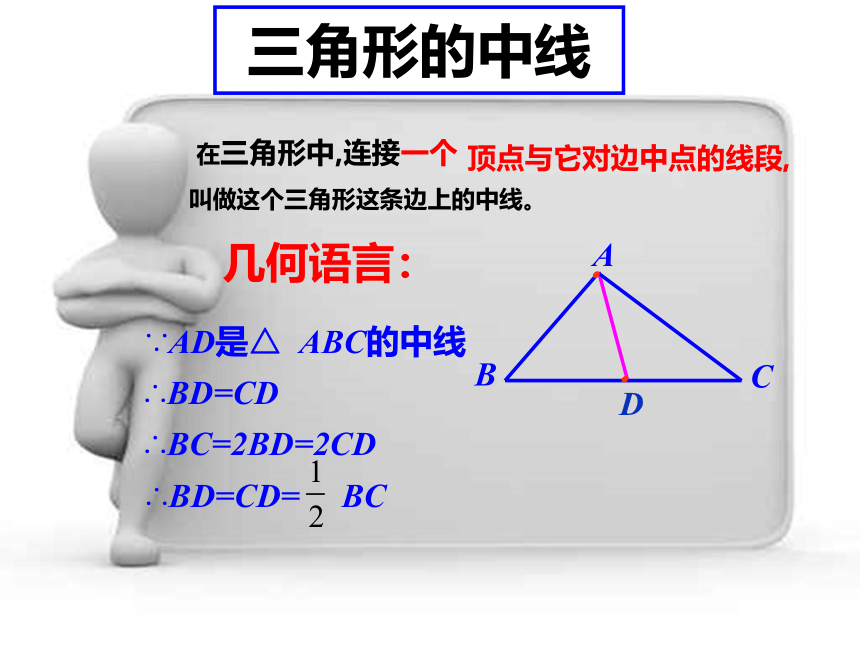
三角形的中线
在三角形中,连接一个
顶点与它对边中点的线段,
叫做这个三角形这条边上的中线。
A
B
C
D
∵AD是△ ABC的中线
∴BD=CD
●
●
几何语言:
∴BC=2BD=2CD
∴BD=CD= BC
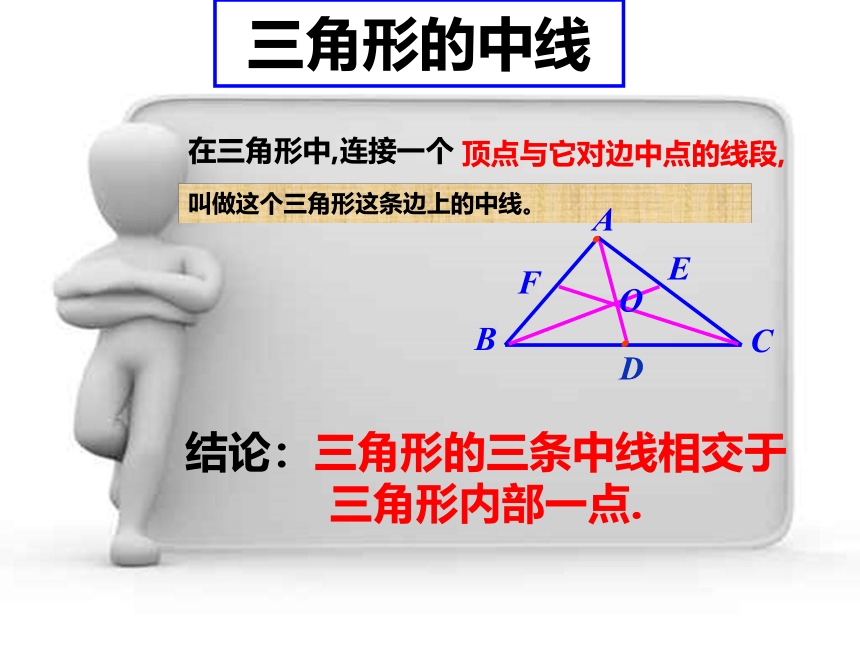
三角形的中线
在三角形中,连接一个
顶点与它对边中点的线段,
叫做这个三角形这条边上的中线。
A
B
C
D
●
●
E
F
O
结论:三角形的三条中线相交于
三角形内部一点.
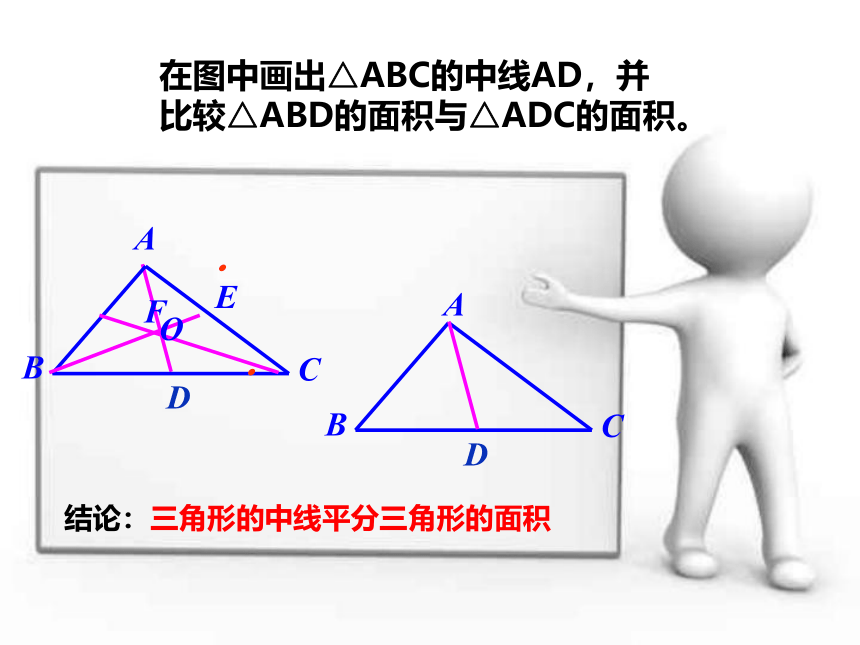
结论:三角形的中线平分三角形的面积
A
B
C
D
在图中画出△ABC的中线AD,并比较△ABD的面积与△ADC的面积。
A
B
C
D
●
●
E
F
O
过一点画已知直线的垂线
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画法
过三角形的一个顶点,你能画出它的对边的垂线吗
B
A
C
三角形的高
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形这边上的高,
简称三角形的高。
∵AD是△ ABC的高
A
B
C
D
∴∠ BDA = ∠ CDA =90°
几何语言
∴AD⊥BC
应用:
求三角形的面积
锐角三角形的三条高
锐角三角形的三条高交于三角形内部一点.
O
锐角三角形的三条高都在三角形的内部。
A
B
C
D
E
F
直角三角形的三条高
A
B
C
直角边BC边上的高是_______;
AB
直角边AB边上的高是_______;
CB
直角三角形的三条高交于直角顶点.
D
斜边AC边上的高是 ;
BD
●
钝角三角形的三条高
A
B
C
D
E
F
钝 角三角形的
三条高不相交于一点
钝角三角形的三条高所在直线交于三角形外部一点
O
小结:三角形的高
从三角形中的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形这条边上的高。
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
结论:三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
今天我们学了什么?
1.三角形的高、中线、角平分线等有关
概念及它们的画法。
2. 三角形的高、中线、角平分线
几何表达及简单应用。
知识小结
思考题:
在等腰△ABC中,AB=AC,一腰
上中线BD将三角形周长分为12和21
两部分,求这个三角形的腰长。
三角形的
重要线段 概念 图形 表示法
三角形
的高线 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段 ∵AD是△ABC的BC上的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
三角形
的中线 三角形中,连结一个顶点和它对边中的
线段 ∵ AD是△ABC的BC上的中线.
∴ BD=CD= BC.
三角形的
角平分线 三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段 ∵.AD是△ABC的角平分线
∴ ∠1=∠2= ∠BAC
11.1.2三角形的高.中线与角平分线
2.线段中点的定义
1.角平分线的定义
3.垂线的定义
复习
三角形的角平分线
叫做三角形的角平分线。
A
B
C
D
∵AD是 △ ABC的角平分线
∴∠ 1 = ∠2
●
●
在三角形中,一个
角的角平分线与它的对边相交,
这个角的顶点与交点之间的线段,
︶
︶
1
2
几何语言:
∴∠ BAC = 2∠1= 2∠2
∴∠ 1 = 2=
∠ BAC
A
C
B
F
E
D
O
三角形的角平分线
结论:三角形的三条角平分线相交于
三角形内部一点。
三角形的中线
在三角形中,连接一个
顶点与它对边中点的线段,
叫做这个三角形这条边上的中线。
A
B
C
D
∵AD是△ ABC的中线
∴BD=CD
●
●
几何语言:
∴BC=2BD=2CD
∴BD=CD= BC
三角形的中线
在三角形中,连接一个
顶点与它对边中点的线段,
叫做这个三角形这条边上的中线。
A
B
C
D
●
●
E
F
O
结论:三角形的三条中线相交于
三角形内部一点.
结论:三角形的中线平分三角形的面积
A
B
C
D
在图中画出△ABC的中线AD,并比较△ABD的面积与△ADC的面积。
A
B
C
D
●
●
E
F
O
过一点画已知直线的垂线
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画法
过三角形的一个顶点,你能画出它的对边的垂线吗
B
A
C
三角形的高
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形这边上的高,
简称三角形的高。
∵AD是△ ABC的高
A
B
C
D
∴∠ BDA = ∠ CDA =90°
几何语言
∴AD⊥BC
应用:
求三角形的面积
锐角三角形的三条高
锐角三角形的三条高交于三角形内部一点.
O
锐角三角形的三条高都在三角形的内部。
A
B
C
D
E
F
直角三角形的三条高
A
B
C
直角边BC边上的高是_______;
AB
直角边AB边上的高是_______;
CB
直角三角形的三条高交于直角顶点.
D
斜边AC边上的高是 ;
BD
●
钝角三角形的三条高
A
B
C
D
E
F
钝 角三角形的
三条高不相交于一点
钝角三角形的三条高所在直线交于三角形外部一点
O
小结:三角形的高
从三角形中的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形这条边上的高。
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
结论:三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
今天我们学了什么?
1.三角形的高、中线、角平分线等有关
概念及它们的画法。
2. 三角形的高、中线、角平分线
几何表达及简单应用。
知识小结
思考题:
在等腰△ABC中,AB=AC,一腰
上中线BD将三角形周长分为12和21
两部分,求这个三角形的腰长。
三角形的
重要线段 概念 图形 表示法
三角形
的高线 从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段 ∵AD是△ABC的BC上的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
三角形
的中线 三角形中,连结一个顶点和它对边中的
线段 ∵ AD是△ABC的BC上的中线.
∴ BD=CD= BC.
三角形的
角平分线 三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段 ∵.AD是△ABC的角平分线
∴ ∠1=∠2= ∠BAC
