上海市徐汇区位育中学2021-2022学年上学期12月月考九年级数学试卷(Word版含答案)
文档属性
| 名称 | 上海市徐汇区位育中学2021-2022学年上学期12月月考九年级数学试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 254.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 22:56:10 | ||
图片预览

文档简介
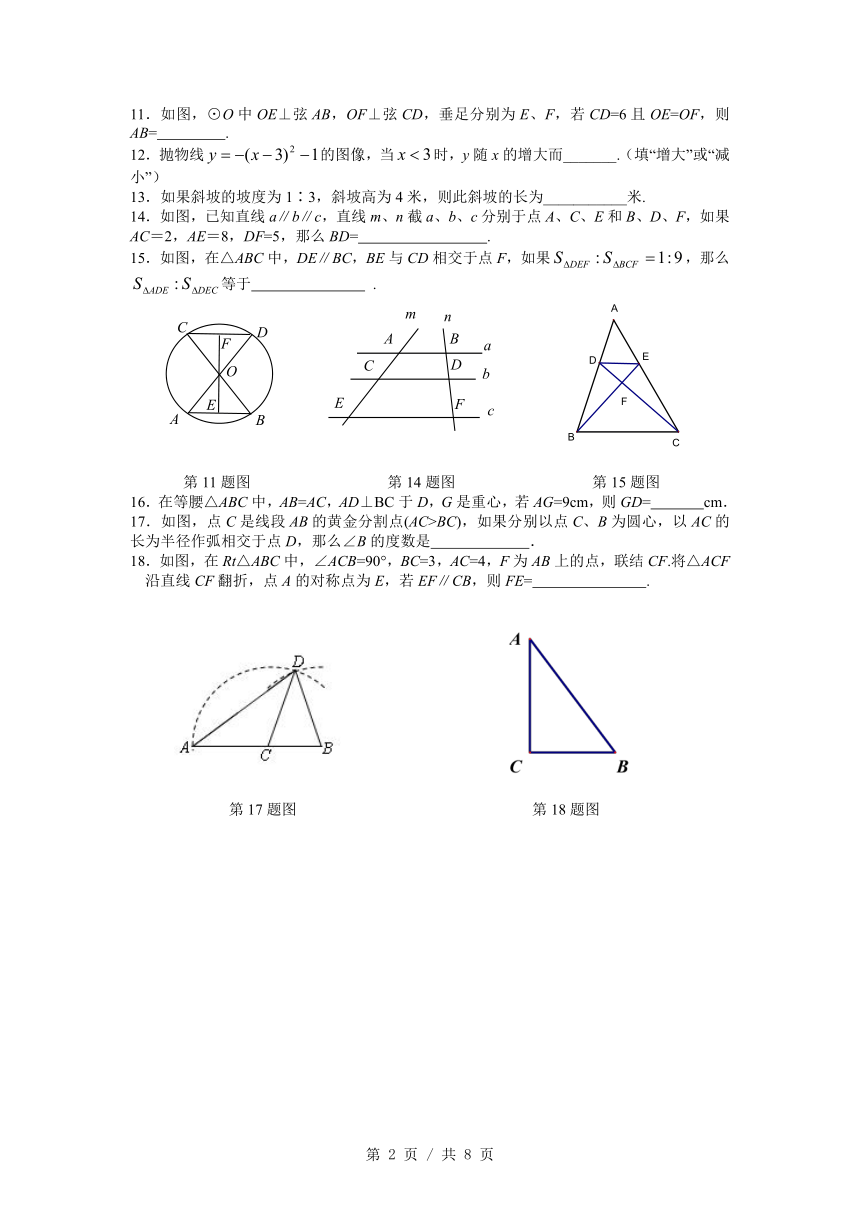
2021学年第一学期九年级12月月考数学试卷
一、选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】
1.将抛物线向右平移个单位,再向下平移个单位得到抛物线的表达式是( )
(A) (B) (C) (D)
2. 如图,在直角坐标平面内有一点,那么射线与轴正半轴的夹角的正切值是( )
(A); (B); (C); (D).
第2题图 第4题图 第6题图
3.下列四个命题中正确的是( )
(A)菱形都相似;
(B)等腰三角形都相似;
(C)两边及其中一边上的中线对应成比例的两三角形相似;
(D)两边对应成比例,且有一个角对应相等的两三角形相似.
4.如图,H是平行四边形ABCD的边AD上一点,且,BH与AC相交于点K,那么AK:KC等于( )
(A)1:1 (B)1:2 (C)1:3 (D)1:4
5.已知⊙O的半径为3cm,在平面内有一点A,且OA=6cm,则点A与⊙O的位置关系是( )
(A)点A在⊙O内 ; (B)点A在⊙O上;
(C)点A在⊙O外; (D)不能确定.
6.如图,已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的角平分线与边AC交于点E,交AD于F,那么下列结论中错误的是 ( )
(A)△BAC∽△BDA; (B)△BDF∽△BEC;
(C)△BFA∽△BEC; (D)△BDF∽△BAE.
二、填空题:(本大题共12题,每题4分,满分48分)
【请将结果直接填入答题纸的相应位置上】
7.若在比例尺为的地图上,测得两地的距离为1.5厘米,则这两地的实际距离
是 千米.
8.已知P是线段AB的一个黄金分割点,且AB=20cm,AP>BP,那么AP= cm.
9.在Rt△ABC中,∠C=90°,如果sinA=,且AB=10,则BC= .
10.若二次函数的图像顶点在y轴上,则m= .
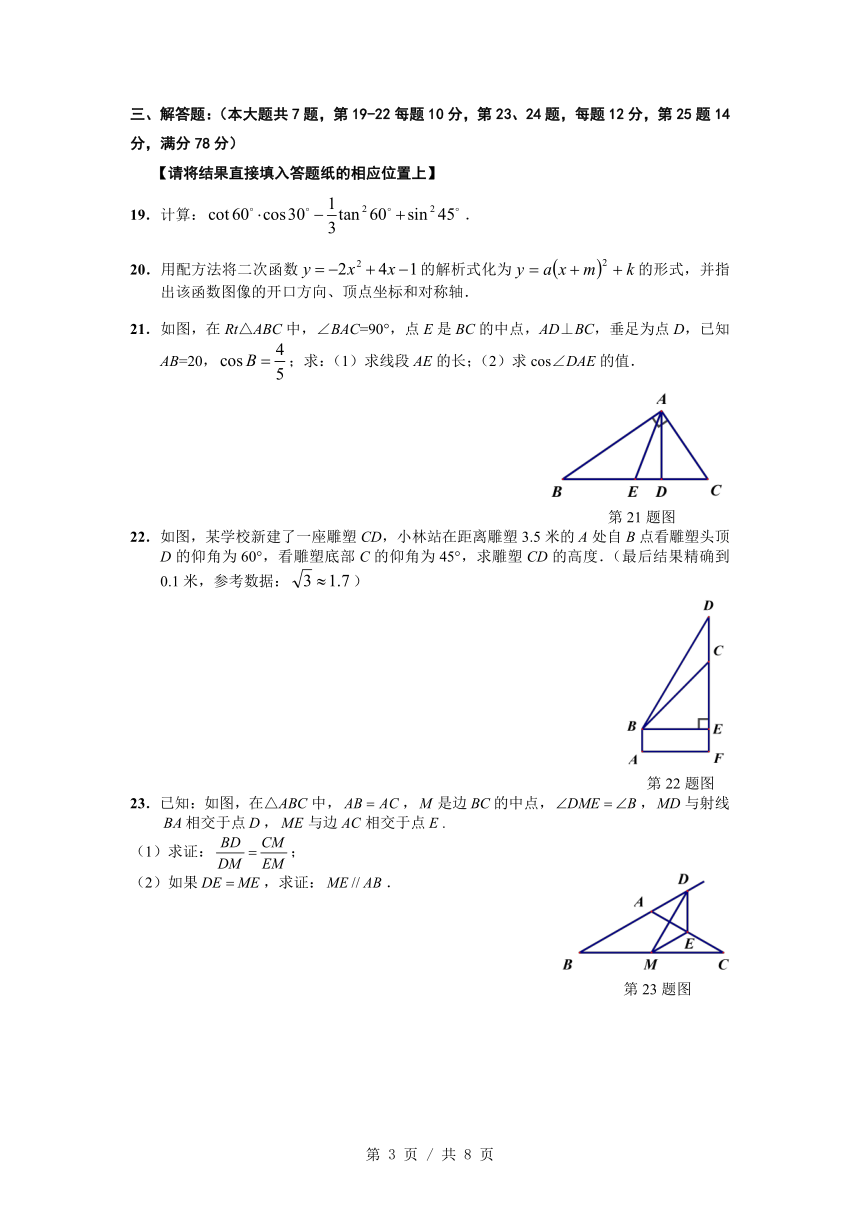
11.如图,⊙O中OE⊥弦AB,OF⊥弦CD,垂足分别为E、F,若CD=6且OE=OF,则AB= .
12.抛物线的图像,当时,y随x的增大而_______.(填“增大”或“减小”)
13.如果斜坡的坡度为1∶3,斜坡高为4米,则此斜坡的长为___________米.
14.如图,已知直线a∥b∥c,直线m、n截a、b、c分别于点A、C、E和B、D、F,如果AC=2,AE=8,DF=5,那么BD= .
15.如图,在△ABC中,DE∥BC,BE与CD相交于点F,如果,那么等于 .
第11题图 第14题图 第15题图
16.在等腰△ABC中,AB=AC,AD⊥BC于D,G是重心,若AG=9cm,则GD= cm.
17.如图,点C是线段AB的黄金分割点(AC>BC),如果分别以点C、B为圆心,以AC的长为半径作弧相交于点D,那么∠B的度数是 .
18.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,F为AB上的点,联结CF.将△ACF沿直线CF翻折,点A的对称点为E,若EF∥CB,则FE= .
第17题图 第18题图
三、解答题:(本大题共7题,第19-22每题10分,第23、24题,每题12分,第25题14分,满分78分)
【请将结果直接填入答题纸的相应位置上】
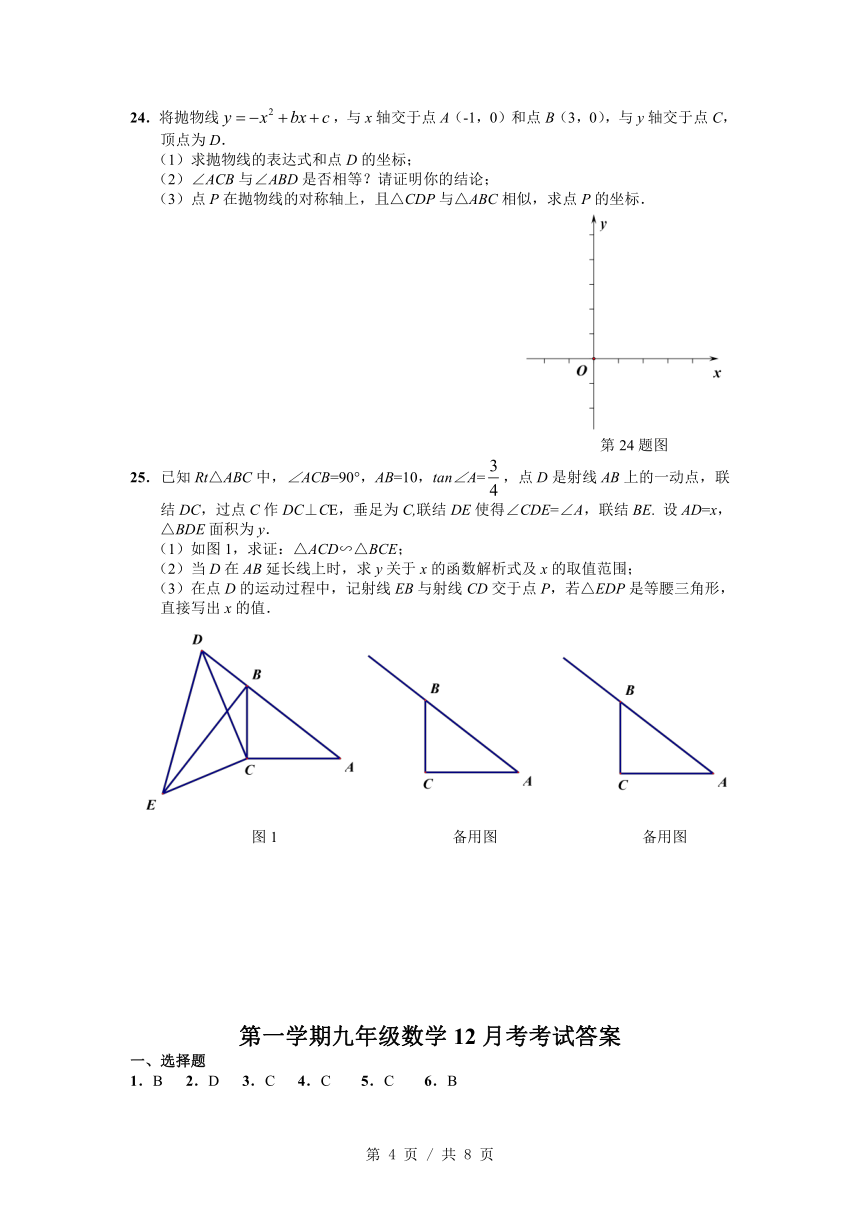
19.计算:.
20.用配方法将二次函数的解析式化为的形式,并指出该函数图像的开口方向、顶点坐标和对称轴.
21.如图,在Rt△ABC中,∠BAC=90°,点E是BC的中点,AD⊥BC,垂足为点D,已知AB=20,;求:(1)求线段AE的长;(2)求cos∠DAE的值.
第21题图
22.如图,某学校新建了一座雕塑CD,小林站在距离雕塑3.5米的A处自B点看雕塑头顶D的仰角为60°,看雕塑底部C的仰角为45°,求雕塑CD的高度.(最后结果精确到0.1米,参考数据:)
第22题图
23.已知:如图,在△ABC中,,是边的中点,,与射线相交于点,与边相交于点.
(1)求证:;
(2)如果,求证:.
第23题图
24.将抛物线,与x轴交于点A(-1,0)和点B(3,0),与y轴交于点C,顶点为D.
(1)求抛物线的表达式和点D的坐标;
(2)∠ACB与∠ABD是否相等?请证明你的结论;
(3)点P在抛物线的对称轴上,且△CDP与△ABC相似,求点P的坐标.
第24题图
25.已知Rt△ABC中,∠ACB=90°,AB=10,tan∠A=,点D是射线AB上的一动点,联结DC,过点C作DC⊥CE,垂足为C,联结DE使得∠CDE=∠A,联结BE. 设AD=x,△BDE面积为y.
(1)如图1,求证:△ACD∽△BCE;
(2)当D在AB延长线上时,求y关于x的函数解析式及x的取值范围;
(3)在点D的运动过程中,记射线EB与射线CD交于点P,若△EDP是等腰三角形,直接写出x的值.
图1 备用图 备用图
第一学期九年级数学12月考考试答案
一、选择题
1.B 2.D 3.C 4.C 5.C 6.B
二、填空题
7 15 8 9 8
10 11 6 12 增大
13 14 15 1:2
16 4.5 17 72° 18 2
三、解答题
19.
解:
20.
开口向下………………………………2分
顶点(1,1)……………………………2分
对称轴:直线x=1………………………2分
21.
22.
23.
证明:
(1)∵AB=AC
∴∠B=∠C 1分
∵∠DMC=∠DME+∠EMC=∠B+∠BDM
∠B=∠DME
∴∠EMC=∠BDM 1分
∴△BDM∽△CME 1分
∴ 1分
∴ 1分
∵M是BC中点
∴BM=MC
∵
∴ 2分
∵∠B=∠DME 1分
∴△BMD∽△MED
∴∠BDM=∠MDE 1分
∵DE=ME
∴∠MDE=∠DME 1分
∴∠DME=∠BDM 1分
∴ 1分
24.
25.
(2)证出∠DBE=90° ……………………………………………………………2分
求出BE= ………………………………………………………………1分
………………………………1分
x>10 …………………………………………………………………………………1分
(3)8或 ………………………………………………………………………2分一个
A
C
E
D
F
B
y
x
O
P
.
A
B
O
D
C
F
E
a
b
c
A
B
C
D
E
F
m
n
4
第 1 页 / 共 9 页
一、选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】
1.将抛物线向右平移个单位,再向下平移个单位得到抛物线的表达式是( )
(A) (B) (C) (D)
2. 如图,在直角坐标平面内有一点,那么射线与轴正半轴的夹角的正切值是( )
(A); (B); (C); (D).
第2题图 第4题图 第6题图
3.下列四个命题中正确的是( )
(A)菱形都相似;
(B)等腰三角形都相似;
(C)两边及其中一边上的中线对应成比例的两三角形相似;
(D)两边对应成比例,且有一个角对应相等的两三角形相似.
4.如图,H是平行四边形ABCD的边AD上一点,且,BH与AC相交于点K,那么AK:KC等于( )
(A)1:1 (B)1:2 (C)1:3 (D)1:4
5.已知⊙O的半径为3cm,在平面内有一点A,且OA=6cm,则点A与⊙O的位置关系是( )
(A)点A在⊙O内 ; (B)点A在⊙O上;
(C)点A在⊙O外; (D)不能确定.
6.如图,已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的角平分线与边AC交于点E,交AD于F,那么下列结论中错误的是 ( )
(A)△BAC∽△BDA; (B)△BDF∽△BEC;
(C)△BFA∽△BEC; (D)△BDF∽△BAE.
二、填空题:(本大题共12题,每题4分,满分48分)
【请将结果直接填入答题纸的相应位置上】
7.若在比例尺为的地图上,测得两地的距离为1.5厘米,则这两地的实际距离
是 千米.
8.已知P是线段AB的一个黄金分割点,且AB=20cm,AP>BP,那么AP= cm.
9.在Rt△ABC中,∠C=90°,如果sinA=,且AB=10,则BC= .
10.若二次函数的图像顶点在y轴上,则m= .
11.如图,⊙O中OE⊥弦AB,OF⊥弦CD,垂足分别为E、F,若CD=6且OE=OF,则AB= .
12.抛物线的图像,当时,y随x的增大而_______.(填“增大”或“减小”)
13.如果斜坡的坡度为1∶3,斜坡高为4米,则此斜坡的长为___________米.
14.如图,已知直线a∥b∥c,直线m、n截a、b、c分别于点A、C、E和B、D、F,如果AC=2,AE=8,DF=5,那么BD= .
15.如图,在△ABC中,DE∥BC,BE与CD相交于点F,如果,那么等于 .
第11题图 第14题图 第15题图
16.在等腰△ABC中,AB=AC,AD⊥BC于D,G是重心,若AG=9cm,则GD= cm.
17.如图,点C是线段AB的黄金分割点(AC>BC),如果分别以点C、B为圆心,以AC的长为半径作弧相交于点D,那么∠B的度数是 .
18.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,F为AB上的点,联结CF.将△ACF沿直线CF翻折,点A的对称点为E,若EF∥CB,则FE= .
第17题图 第18题图
三、解答题:(本大题共7题,第19-22每题10分,第23、24题,每题12分,第25题14分,满分78分)
【请将结果直接填入答题纸的相应位置上】
19.计算:.
20.用配方法将二次函数的解析式化为的形式,并指出该函数图像的开口方向、顶点坐标和对称轴.
21.如图,在Rt△ABC中,∠BAC=90°,点E是BC的中点,AD⊥BC,垂足为点D,已知AB=20,;求:(1)求线段AE的长;(2)求cos∠DAE的值.
第21题图
22.如图,某学校新建了一座雕塑CD,小林站在距离雕塑3.5米的A处自B点看雕塑头顶D的仰角为60°,看雕塑底部C的仰角为45°,求雕塑CD的高度.(最后结果精确到0.1米,参考数据:)
第22题图
23.已知:如图,在△ABC中,,是边的中点,,与射线相交于点,与边相交于点.
(1)求证:;
(2)如果,求证:.
第23题图
24.将抛物线,与x轴交于点A(-1,0)和点B(3,0),与y轴交于点C,顶点为D.
(1)求抛物线的表达式和点D的坐标;
(2)∠ACB与∠ABD是否相等?请证明你的结论;
(3)点P在抛物线的对称轴上,且△CDP与△ABC相似,求点P的坐标.
第24题图
25.已知Rt△ABC中,∠ACB=90°,AB=10,tan∠A=,点D是射线AB上的一动点,联结DC,过点C作DC⊥CE,垂足为C,联结DE使得∠CDE=∠A,联结BE. 设AD=x,△BDE面积为y.
(1)如图1,求证:△ACD∽△BCE;
(2)当D在AB延长线上时,求y关于x的函数解析式及x的取值范围;
(3)在点D的运动过程中,记射线EB与射线CD交于点P,若△EDP是等腰三角形,直接写出x的值.
图1 备用图 备用图
第一学期九年级数学12月考考试答案
一、选择题
1.B 2.D 3.C 4.C 5.C 6.B
二、填空题
7 15 8 9 8
10 11 6 12 增大
13 14 15 1:2
16 4.5 17 72° 18 2
三、解答题
19.
解:
20.
开口向下………………………………2分
顶点(1,1)……………………………2分
对称轴:直线x=1………………………2分
21.
22.
23.
证明:
(1)∵AB=AC
∴∠B=∠C 1分
∵∠DMC=∠DME+∠EMC=∠B+∠BDM
∠B=∠DME
∴∠EMC=∠BDM 1分
∴△BDM∽△CME 1分
∴ 1分
∴ 1分
∵M是BC中点
∴BM=MC
∵
∴ 2分
∵∠B=∠DME 1分
∴△BMD∽△MED
∴∠BDM=∠MDE 1分
∵DE=ME
∴∠MDE=∠DME 1分
∴∠DME=∠BDM 1分
∴ 1分
24.
25.
(2)证出∠DBE=90° ……………………………………………………………2分
求出BE= ………………………………………………………………1分
………………………………1分
x>10 …………………………………………………………………………………1分
(3)8或 ………………………………………………………………………2分一个
A
C
E
D
F
B
y
x
O
P
.
A
B
O
D
C
F
E
a
b
c
A
B
C
D
E
F
m
n
4
第 1 页 / 共 9 页
同课章节目录
