沪科版数学九年级上册 第22章 相似形综合题课件(共19张ppt)
文档属性
| 名称 | 沪科版数学九年级上册 第22章 相似形综合题课件(共19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 12:43:58 | ||
图片预览




文档简介
(共19张PPT)
第22章 相似形(通用)
知识点回顾
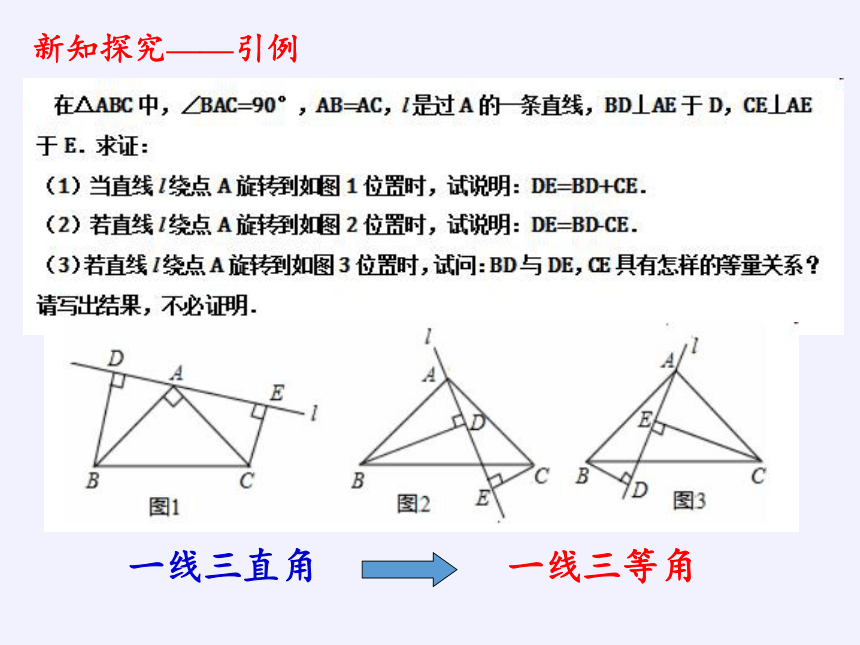
新知探究——引例
一线三直角
一线三等角
例题1
小试牛刀
例题2
一线二等角
真题展示
E
E
小结
同学们这节课你有哪些收获?
请大家相互交流,总结一下!
作业
2.名冠经典P80页,第12题
谢 谢
相似图形的定义、实质、及性质
1.形状相同的图形
①表象:大小不等,形状相同
②实质:各对应角相等、各对应边成比例
2.相似多边形
各对应角相等、各对应边成比例的两个多边形
叫做相似多边形.相似多边形对应边的比叫做相
似比(相似比与叙述的顺序有关)
3.相似多边形性质:
①相似多边形的对应角相等,对应边成比例
②相似多边形周长的比等于相似比
③相似多边形面积的比等于相似比的平方
4.相似三角形
三个对应角相等、三条对应边成比例的两个
角形叫做相似三角形.相似三角形对应边的比叫
做相似比(相似比与叙述的顺序有关)
5相似三角形性质:
①相似三角形的对应角相等,对应边成比例
②相似三角形对应中线的比对应角平分线的比,
对应高的比对应周长的比都等于相似比
③相似三角形面积的比等于相似比的平方
6似三角形与全等三角形的关系
相似比等于1的两个三角形全等
7两个极具代表性的益智“模型”:“A”型和
“X”型相似三角形
D
A
角形相似的判定方法有哪些
预备定理平行于三角形一边直线截其它两
边〔或其延长线)所截得的三角形与原三角形相似
2.定理三边对应成比例的两个三角形相似
3.定理两边对应成比例,且夹角相等的两个三
角形相似
4.定理有两个角对应相等的两个三角形相似
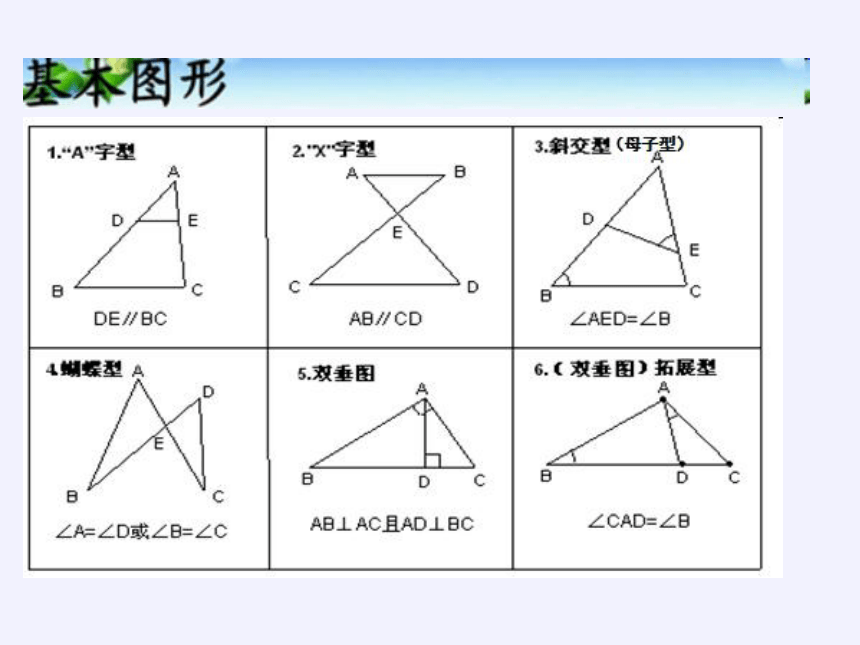
1“A"字型
2X宇型
3斜交型〔母子型)
D
DE∥BC
AB∥CD
∠AED=∠B
4蝴蟻型A
5双垂图
6.(双垂图〕拓展型
∠A=∠D或∠B=∠C
AB⊥AC且AD⊥BC
∠CAD=∠B
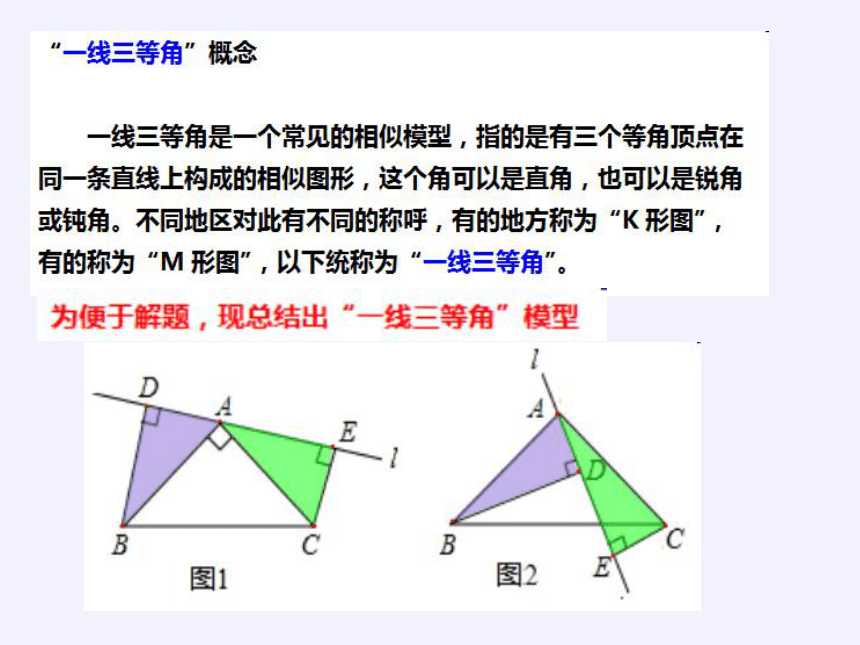
、“一线三等角”的性质
1、一般情况下,由∠1=∠2=∠3,易得△AEC∽△BDE
2、当等角所对的边相等时,两个三角形全等
如图,当CE=ED时,易得△AEC≌BDE
D
A
E
B
3、中点型一线三等角
当∠1=∠2=∠3且点E是AB中点时,
△AEC△BDE△EDC
1
E
B
例.如图,在△ABC中,已知AB=AC=5,BC
=6,且△ABC≌△DEF,将△DEF与△ABC重合在
一起,△ABC不动,△DEF运动,并满足:点E在边
BC上沿B到C的方向运动,且DE始终经过点A
EF与AC交于M点
(1)求证:△ABEU△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否
构成等腰三角形,若能,求出BE的长;若不能,请说
明理由;
第22章 相似形(通用)
知识点回顾
新知探究——引例
一线三直角
一线三等角
例题1
小试牛刀
例题2
一线二等角
真题展示
E
E
小结
同学们这节课你有哪些收获?
请大家相互交流,总结一下!
作业
2.名冠经典P80页,第12题
谢 谢
相似图形的定义、实质、及性质
1.形状相同的图形
①表象:大小不等,形状相同
②实质:各对应角相等、各对应边成比例
2.相似多边形
各对应角相等、各对应边成比例的两个多边形
叫做相似多边形.相似多边形对应边的比叫做相
似比(相似比与叙述的顺序有关)
3.相似多边形性质:
①相似多边形的对应角相等,对应边成比例
②相似多边形周长的比等于相似比
③相似多边形面积的比等于相似比的平方
4.相似三角形
三个对应角相等、三条对应边成比例的两个
角形叫做相似三角形.相似三角形对应边的比叫
做相似比(相似比与叙述的顺序有关)
5相似三角形性质:
①相似三角形的对应角相等,对应边成比例
②相似三角形对应中线的比对应角平分线的比,
对应高的比对应周长的比都等于相似比
③相似三角形面积的比等于相似比的平方
6似三角形与全等三角形的关系
相似比等于1的两个三角形全等
7两个极具代表性的益智“模型”:“A”型和
“X”型相似三角形
D
A
角形相似的判定方法有哪些
预备定理平行于三角形一边直线截其它两
边〔或其延长线)所截得的三角形与原三角形相似
2.定理三边对应成比例的两个三角形相似
3.定理两边对应成比例,且夹角相等的两个三
角形相似
4.定理有两个角对应相等的两个三角形相似
1“A"字型
2X宇型
3斜交型〔母子型)
D
DE∥BC
AB∥CD
∠AED=∠B
4蝴蟻型A
5双垂图
6.(双垂图〕拓展型
∠A=∠D或∠B=∠C
AB⊥AC且AD⊥BC
∠CAD=∠B
、“一线三等角”的性质
1、一般情况下,由∠1=∠2=∠3,易得△AEC∽△BDE
2、当等角所对的边相等时,两个三角形全等
如图,当CE=ED时,易得△AEC≌BDE
D
A
E
B
3、中点型一线三等角
当∠1=∠2=∠3且点E是AB中点时,
△AEC△BDE△EDC
1
E
B
例.如图,在△ABC中,已知AB=AC=5,BC
=6,且△ABC≌△DEF,将△DEF与△ABC重合在
一起,△ABC不动,△DEF运动,并满足:点E在边
BC上沿B到C的方向运动,且DE始终经过点A
EF与AC交于M点
(1)求证:△ABEU△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否
构成等腰三角形,若能,求出BE的长;若不能,请说
明理由;
