2021—2022学年华东师大版八年级数学下册19.3正方形 练习题(Word版含答案)
文档属性
| 名称 | 2021—2022学年华东师大版八年级数学下册19.3正方形 练习题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 140.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 13:57:20 | ||
图片预览



文档简介
19.3 正方形
一选择题
1.正方形具有而菱形不一定具有的性质是 ( )
A.四条边相等
B.对角线互相垂直平分
C.对角线平分一组对角
D.对角线相等
2.下列命题是假命题的是 ( )
A.对角线互相垂直且相等的平行四边形是正方形
B.对角线互相垂直的矩形是正方形
C.对角线相等的菱形是正方形
D.对角线互相垂直且平分的四边形是正方形
3.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH的长是 ( )
A.3 B.4 C.5 D.6
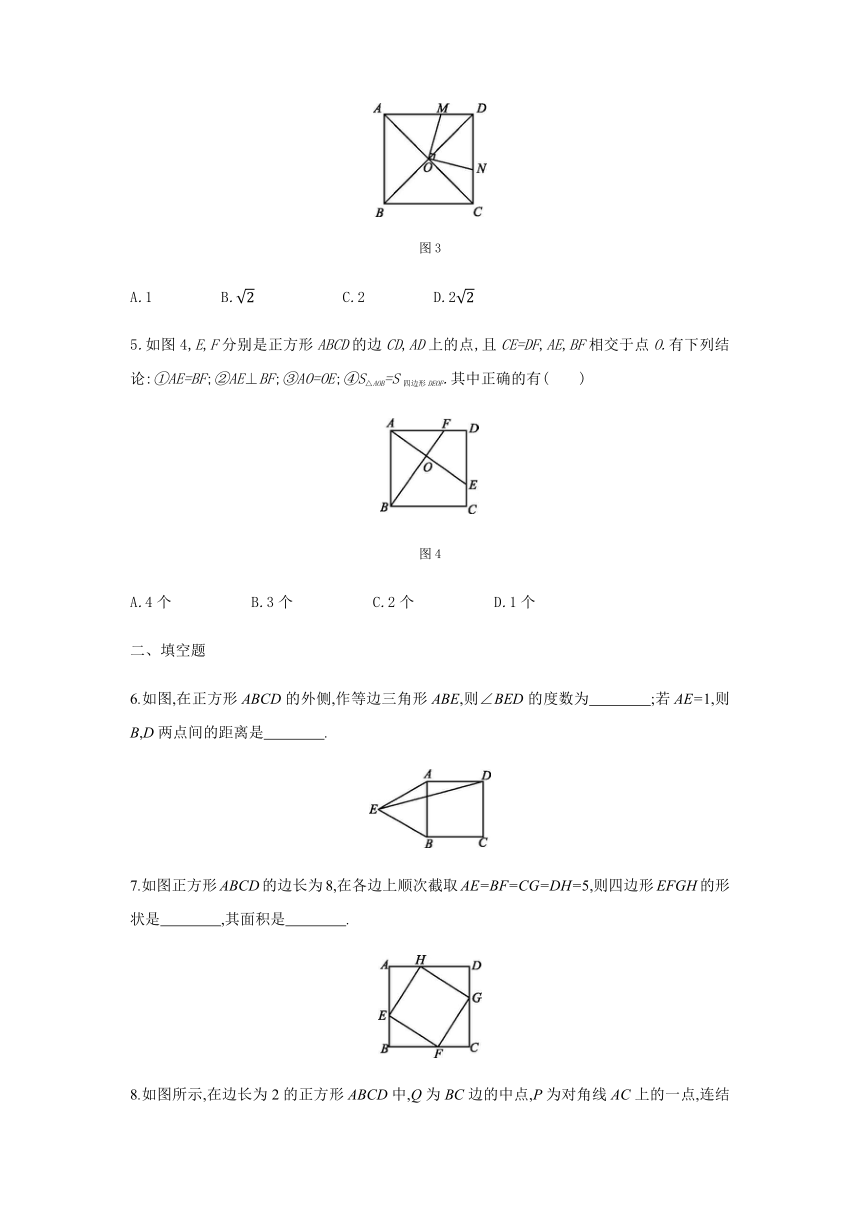
4.如图3,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连结OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为 ( )
图3
A.1 B. C.2 D.2
5.如图4,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O.有下列结论:①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF.其中正确的有( )
图4
A.4个 B.3个 C.2个 D.1个
填空题
6.如图,在正方形ABCD的外侧,作等边三角形ABE,则∠BED的度数为 ;若AE=1,则B,D两点间的距离是 .
7.如图正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的形状是 ,其面积是 .
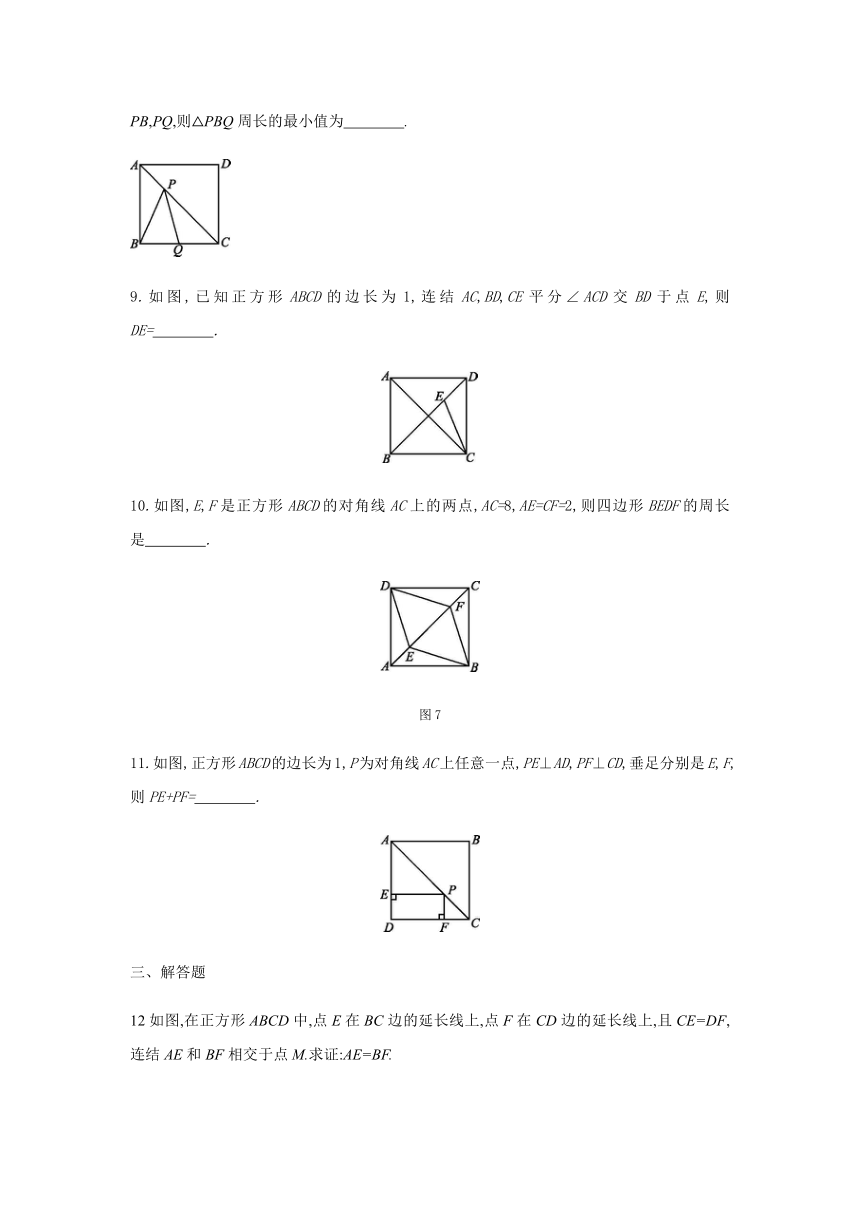
8.如图所示,在边长为2的正方形ABCD中,Q为BC边的中点,P为对角线AC上的一点,连结PB,PQ,则△PBQ周长的最小值为 .
9.如图,已知正方形ABCD的边长为1,连结AC,BD,CE平分∠ACD交BD于点E,则DE= .
10.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 .
图7
11.如图,正方形ABCD的边长为1,P为对角线AC上任意一点,PE⊥AD,PF⊥CD,垂足分别是E,F,则PE+PF= .
解答题
12如图,在正方形ABCD中,点E在BC边的延长线上,点F在CD边的延长线上,且CE=DF,连结AE和BF相交于点M.求证:AE=BF.
13.已知:如图,在Rt△ABC中,∠C=90°,∠BAC,∠ABC的平分线相交于点D,DE⊥BC,DF⊥AC,垂足分别为E,F.
求证:四边形CEDF是正方形.
14.如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
15.如图,在△ABC中,D为BC边上的一个动点(点D不与B,C两点重合),DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)试探索当AD满足什么条件时,四边形AEDF为菱形,并说明理由;
(2)在(1)的条件下,△ABC满足什么条件时,四边形AEDF为正方形 为什么
16在正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N,AH⊥MN于点H.
(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系: .
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗 如果不成立,请说明理由;如果成立,请进行证明.
19.3 正方形
1.D 2.D 3.B 4.C 5.B
645°
7正方形 34
+1
9.+1 .
10.-1
11.4
12.证明:∵四边形ABCD是正方形,
∴AB=BC=CD,∠ABE=∠BCF=90°.
∵CE=DF,∴BC+CE=CD+DF,即BE=CF.
在△AEB与△BFC中,
∵AB=BC,∠ABE=∠BCF,BE=CF,
∴△AEB≌△BFC,
∴AE=BF.
13证明:如图,过点D作DN⊥AB于点N.
∵DE⊥BC,DF⊥AC,
∴∠DFC=∠DEC=90°.
又∵∠C=90°,
∴四边形CEDF是矩形.
∵∠BAC,∠ABC的平分线相交于点D,DF⊥AC,DN⊥AB,DE⊥BC,
∴DF=DN,DE=DN,∴DF=DE,
∴四边形CEDF是正方形.
14.证明:(1)∵AB=AC,
∴∠B=∠C.
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵D为BC边的中点,
∴BD=CD,∴△BED≌△CFD.
(2)∵∠BED=∠CFD=90°,
∴∠AED=∠AFD=90°.
又∵∠A=90°,
∴四边形DFAE是矩形.
由(1)知△BED≌△CFD,
∴DE=DF,
∴四边形DFAE是正方形.
15.解:(1)当AD平分∠BAC时,四边形AEDF为菱形.
理由:∵AE∥DF,DE∥AF,
∴四边形AEDF为平行四边形,∠FAD=∠ADE.
∵AD平分∠BAC,
∴∠EAD=∠FAD,
∴∠EAD=∠ADE,
∴AE=DE,
∴ AEDF为菱形.
(2)当∠BAC=90°时,菱形AEDF为正方形.
理由:∵有一个角是直角的菱形是正方形,
∴当∠BAC=90°时,菱形AEDF为正方形.
16.解:(1)AH=AB
(2)AH=AB还成立.
证明:如图,延长CB至点E,使BE=DN,连结AE.
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠D=∠ABE=90°.
在△AEB和△AND中,
∵AB=AD,∠ABE=∠D,BE=DN,
∴△AEB≌△AND,
∴AE=AN,∠EAB=∠NAD.
∵∠BAD=90°,∠MAN=45°,
∴∠BAM+∠NAD=45°,
∴∠BAM+∠EAB=45°,
∴∠MAE=45°=∠MAN.
在△AEM和△ANM中,
∵AE=AN,∠MAE=∠MAN,AM=AM,
∴△AEM≌△ANM,
∴S△AEM=S△ANM,EM=MN.
∵AB为△AEM的边EM上的高,AH为△ANM的边MN上的高,
∴AB=AH.
一选择题
1.正方形具有而菱形不一定具有的性质是 ( )
A.四条边相等
B.对角线互相垂直平分
C.对角线平分一组对角
D.对角线相等
2.下列命题是假命题的是 ( )
A.对角线互相垂直且相等的平行四边形是正方形
B.对角线互相垂直的矩形是正方形
C.对角线相等的菱形是正方形
D.对角线互相垂直且平分的四边形是正方形
3.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH的长是 ( )
A.3 B.4 C.5 D.6
4.如图3,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连结OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为 ( )
图3
A.1 B. C.2 D.2
5.如图4,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O.有下列结论:①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF.其中正确的有( )
图4
A.4个 B.3个 C.2个 D.1个
填空题
6.如图,在正方形ABCD的外侧,作等边三角形ABE,则∠BED的度数为 ;若AE=1,则B,D两点间的距离是 .
7.如图正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的形状是 ,其面积是 .
8.如图所示,在边长为2的正方形ABCD中,Q为BC边的中点,P为对角线AC上的一点,连结PB,PQ,则△PBQ周长的最小值为 .
9.如图,已知正方形ABCD的边长为1,连结AC,BD,CE平分∠ACD交BD于点E,则DE= .
10.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 .
图7
11.如图,正方形ABCD的边长为1,P为对角线AC上任意一点,PE⊥AD,PF⊥CD,垂足分别是E,F,则PE+PF= .
解答题
12如图,在正方形ABCD中,点E在BC边的延长线上,点F在CD边的延长线上,且CE=DF,连结AE和BF相交于点M.求证:AE=BF.
13.已知:如图,在Rt△ABC中,∠C=90°,∠BAC,∠ABC的平分线相交于点D,DE⊥BC,DF⊥AC,垂足分别为E,F.
求证:四边形CEDF是正方形.
14.如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
15.如图,在△ABC中,D为BC边上的一个动点(点D不与B,C两点重合),DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)试探索当AD满足什么条件时,四边形AEDF为菱形,并说明理由;
(2)在(1)的条件下,△ABC满足什么条件时,四边形AEDF为正方形 为什么
16在正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N,AH⊥MN于点H.
(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系: .
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗 如果不成立,请说明理由;如果成立,请进行证明.
19.3 正方形
1.D 2.D 3.B 4.C 5.B
645°
7正方形 34
+1
9.+1 .
10.-1
11.4
12.证明:∵四边形ABCD是正方形,
∴AB=BC=CD,∠ABE=∠BCF=90°.
∵CE=DF,∴BC+CE=CD+DF,即BE=CF.
在△AEB与△BFC中,
∵AB=BC,∠ABE=∠BCF,BE=CF,
∴△AEB≌△BFC,
∴AE=BF.
13证明:如图,过点D作DN⊥AB于点N.
∵DE⊥BC,DF⊥AC,
∴∠DFC=∠DEC=90°.
又∵∠C=90°,
∴四边形CEDF是矩形.
∵∠BAC,∠ABC的平分线相交于点D,DF⊥AC,DN⊥AB,DE⊥BC,
∴DF=DN,DE=DN,∴DF=DE,
∴四边形CEDF是正方形.
14.证明:(1)∵AB=AC,
∴∠B=∠C.
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵D为BC边的中点,
∴BD=CD,∴△BED≌△CFD.
(2)∵∠BED=∠CFD=90°,
∴∠AED=∠AFD=90°.
又∵∠A=90°,
∴四边形DFAE是矩形.
由(1)知△BED≌△CFD,
∴DE=DF,
∴四边形DFAE是正方形.
15.解:(1)当AD平分∠BAC时,四边形AEDF为菱形.
理由:∵AE∥DF,DE∥AF,
∴四边形AEDF为平行四边形,∠FAD=∠ADE.
∵AD平分∠BAC,
∴∠EAD=∠FAD,
∴∠EAD=∠ADE,
∴AE=DE,
∴ AEDF为菱形.
(2)当∠BAC=90°时,菱形AEDF为正方形.
理由:∵有一个角是直角的菱形是正方形,
∴当∠BAC=90°时,菱形AEDF为正方形.
16.解:(1)AH=AB
(2)AH=AB还成立.
证明:如图,延长CB至点E,使BE=DN,连结AE.
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠D=∠ABE=90°.
在△AEB和△AND中,
∵AB=AD,∠ABE=∠D,BE=DN,
∴△AEB≌△AND,
∴AE=AN,∠EAB=∠NAD.
∵∠BAD=90°,∠MAN=45°,
∴∠BAM+∠NAD=45°,
∴∠BAM+∠EAB=45°,
∴∠MAE=45°=∠MAN.
在△AEM和△ANM中,
∵AE=AN,∠MAE=∠MAN,AM=AM,
∴△AEM≌△ANM,
∴S△AEM=S△ANM,EM=MN.
∵AB为△AEM的边EM上的高,AH为△ANM的边MN上的高,
∴AB=AH.
