2021-2022学年华东师大版八年级数学下册第17章 函数及其图象单元测试题 (Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学下册第17章 函数及其图象单元测试题 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 108.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 14:06:27 | ||
图片预览




文档简介
第17章 函数及其图象
一、选择题(每小题4分,共28分)
1.在平面直角坐标系中,点(2,-3)所在的象限是 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.直线y=2x-4与y轴的交点坐标是 ( )
A.(4,0) B.(0,4) C.(-4,0) D.(0,-4)
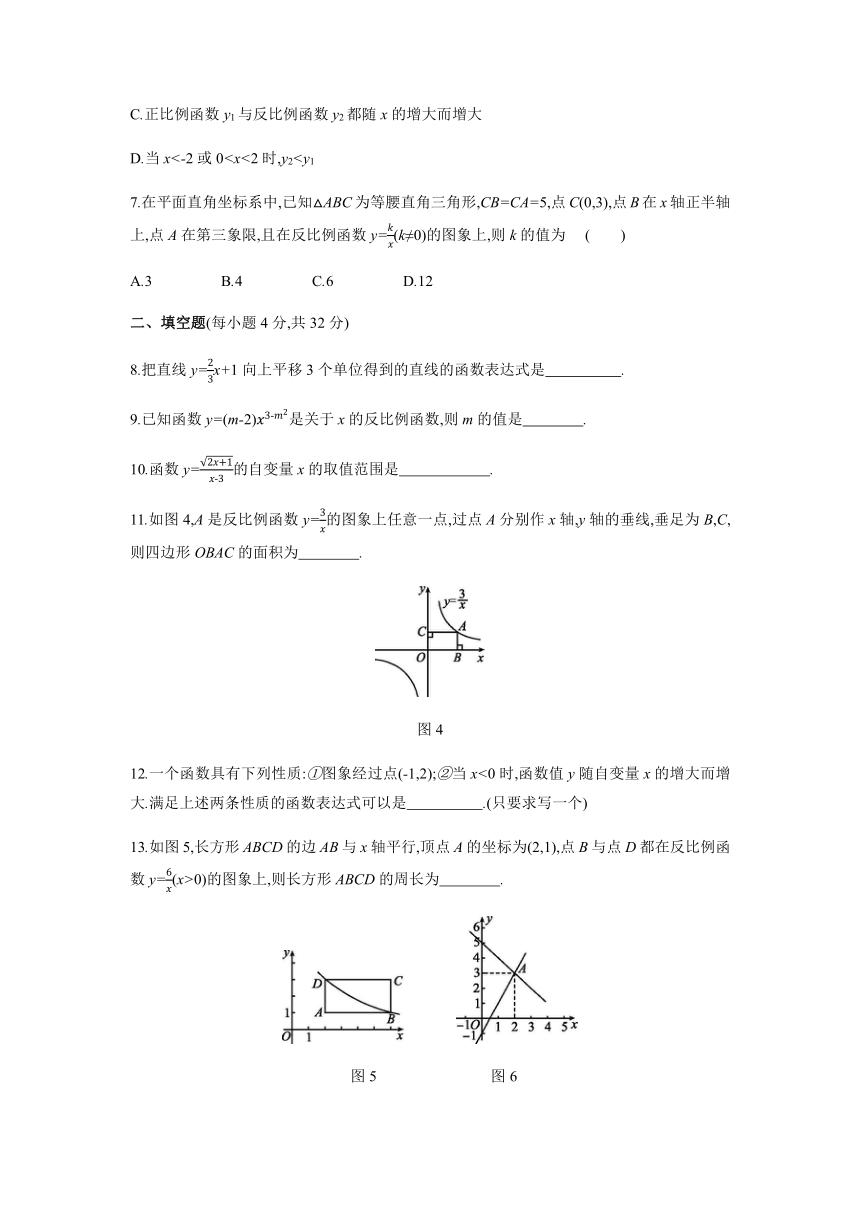
3.已知一次函数y=kx+b(k≠0)的图象如图1所示,当y<0时,x的取值范围是 ( )
A.x>0 B.x<1 C.01
图1 图2
4.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图2所示,则这个反比例函数的表达式为 ( )
A.I= B.I= C.I= D.I=
5.函数y=和y=-kx+2(k≠0)在同一平面直角坐标系中的大致图象可能是 ( )
图3
6.已知正比例函数y1的图象与反比例函数y2的图象相交于点A(-2,4).下列说法正确的是
( )
A.正比例函数y1的表达式是y1=2x
B.两个函数图象的另一交点坐标为(4,-2)
C.正比例函数y1与反比例函数y2都随x的增大而增大
D.当x<-2或07.在平面直角坐标系中,已知△ABC为等腰直角三角形,CB=CA=5,点C(0,3),点B在x轴正半轴上,点A在第三象限,且在反比例函数y=(k≠0)的图象上,则k的值为 ( )
A.3 B.4 C.6 D.12
二、填空题(每小题4分,共32分)
8.把直线y=x+1向上平移3个单位得到的直线的函数表达式是 .
9.已知函数y=(m-2)是关于x的反比例函数,则m的值是 .
10.函数y=的自变量x的取值范围是 .
11.如图4,A是反比例函数y=的图象上任意一点,过点A分别作x轴,y轴的垂线,垂足为B,C,则四边形OBAC的面积为 .
图4
12.一个函数具有下列性质:①图象经过点(-1,2);②当x<0时,函数值y随自变量x的增大而增大.满足上述两条性质的函数表达式可以是 .(只要求写一个)
13.如图5,长方形ABCD的边AB与x轴平行,顶点A的坐标为(2,1),点B与点D都在反比例函数y=(x>0)的图象上,则长方形ABCD的周长为 .
图5 图6
14.如图6,点A的坐标可以看成是方程组 的解.
15.小明从家步行到学校需走的路程为2000米.图7中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分)的函数关系,根据图象提供的信息,当小明从家出发去学校步行20分钟时,距离学校还有 米.
图7
三、解答题(共40分)
16.(12分)在平面直角坐标系中,有一点M(a-1,2a+7),试求满足下列条件的a的值.
(1)点M在x轴上;
(2)点M在第二象限;
(3)点M到y轴的距离是1.
17.(13分)某超市预购进A,B两种品牌的T恤共200件,已知两种T恤的进价和售价如下表所示,设购进A种T恤x件,且所购进的两种T恤全部卖出,获得的总利润为W元.
品牌 进价(元/件) 售价(元/件)
A 50 80
B 40 65
(1)W关于x的函数表达式为 ;
(2)如果购进两种T恤的总费用不超过9500元,那么超市如何进货才能获得最大利润 求出最大利润.(提示:利润=售价-进价)
18.(15分)如图8所示,一次函数y=mx+n(m≠0)的图象与反比例函数y=(k≠0)的图象交于第二、四象限的点A(-2,a)和点B(b,-1),过点A作x轴的垂线,垂足为C,△AOC的面积为4.
(1)a= ,b= ;
(2)结合图象直接写出当mx+n>时x的取值范围为 ;
(3)在y轴上取点P,使PB-PA的值最大,求出点P的坐标.
图8
19 李师傅将容量为60升的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程s(千米)与行驶时间t(时)之间的关系如图所示(中途休息、加油的时间不计).当油箱中剩余油量为10升时,货车会自动显示加油提醒.设货车平均耗油量为0.1升/千米,请根据图象解答下列问题:
(1)直接写出工厂离目的地的路程;
(2)求s关于t的函数表达式;
(3)当货车显示加油提醒后,行驶时间t在怎样的范围内货车应进站加油
20某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍,用80元购买的甲食材比用20元购买的乙食材多1千克.
营养品信息表
营养成分 每千克含铁42毫克
配料表 原料 每千克含铁
甲食材 50毫克
乙食材 10毫克
规格 每包食材含量 每包单价
A包装 1千克 45元
B包装 0.25千克 12元
(1)甲、乙两种食材每千克进价分别是多少元
(2)该公司每日用18000元购进甲、乙两种食材并恰好全部用完.
①每日购进甲、乙两种食材各多少千克
②已知每日其他费用为2000元,且生产的营养品当日全部售出.若A的数量不低于B的数量,则A为多少包时,每日所获总利润最大,最大总利润为多少元
答案
1.D 2.D 3.B 4.C 5.D 6.D 7.A
8.y=x+4
9.-2
10.x≥-且x≠3 .
11.3
12.y=-(答案不唯一)
13.12 .
14.
15.240 .
16.解:(1)要使点M在x轴上,a应满足2a+7=0,解得a=-,
所以当a=-时,点M在x轴上.
(2)要使点M在第二象限,a应满足
解得-所以当-(3)要使点M到y轴的距离是1,a应满足|a-1|=1,解得a=2或a=0,所以当a=2或a=0时,点M到y轴的距离是1.
17.解:(1)W=5x+5000 [解析] 购进A种T恤x件,则购进B种T恤(200-x)件.根据题意,得
W=(80-50)x+(65-40)(200-x)=30x+5000-25x=5x+5000.
(2)因为购进两种T恤的总费用不超过9500元,
所以50x+40(200-x)≤9500,解得x≤150.
因为W=5x+5000中,k=5>0,
所以W随x的增大而增大,
所以当x=150时,W的值最大,最大值为5750.
200-150=50(件).
所以当超市购进A种T恤150件,购进B种T恤50件时,才能获得最大利润,最大利润为5750元.
18.解:(1)4 8
(2)x<-2或0(3)由(1)知A(-2,4),B(8,-1).
如图,作点A关于y轴的对称点A',则A'(2,4),连结BA'并延长交y轴于点P,此时点P即为所求.
设直线A'B的表达式为y=cx+d(c≠0),则解得
所以直线A'B的表达式为y=-x+.
当x=0时,y=,
所以点P的坐标为0,.
19.解:(1)由图象,得t=0时,s=880,
所以工厂离目的地的路程为880千米.
(2)设s关于t的函数表达式为s=kt+b(k≠0),将(0,880)和(4,560)代入得
解得
所以s关于t的函数表达式为s=-80t+880(0≤t≤11).
(3)当油箱中剩余油量为10升时,s=880-(60-10)÷0.1=380(千米),
令380=-80t+880,解得t=;
当油箱中剩余油量为0升时,s=880-60÷0.1=280(千米),
令280=-80t+880,解得t=.
因为k=-80<0,所以s随t的增大而减小,
所以t的取值范围是即当货车显示加油提醒后,行驶时间t在20.解:(1)设乙食材每千克进价为a元,则甲食材每千克进价为2a元,
由题意得-=1,解得a=20.
经检验,a=20是所列方程的根,且符合题意,所以2a=40.
答:甲食材每千克进价为40元,乙食材每千克进价为20元.
(2)①设每日购进甲食材x千克,乙食材y千克,
由题意得
解得
答:每日购进甲食材400千克,乙食材100千克.
②设A为m包,则B为=(2000-4m)包.
因为A的数量不低于B的数量,
所以m≥2000-4m,所以m≥400.
设每日所获总利润为W元,根据题意得
W=45m+12(2000-4m)-18000-2000=-3m+4000.
因为k=-3<0,所以W随m的增大而减小,
所以当m=400时,W取最大值为2800.
答:当A为400包时,每日所获总利润最大,最大总利润为2800元.
一、选择题(每小题4分,共28分)
1.在平面直角坐标系中,点(2,-3)所在的象限是 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.直线y=2x-4与y轴的交点坐标是 ( )
A.(4,0) B.(0,4) C.(-4,0) D.(0,-4)
3.已知一次函数y=kx+b(k≠0)的图象如图1所示,当y<0时,x的取值范围是 ( )
A.x>0 B.x<1 C.0
图1 图2
4.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图2所示,则这个反比例函数的表达式为 ( )
A.I= B.I= C.I= D.I=
5.函数y=和y=-kx+2(k≠0)在同一平面直角坐标系中的大致图象可能是 ( )
图3
6.已知正比例函数y1的图象与反比例函数y2的图象相交于点A(-2,4).下列说法正确的是
( )
A.正比例函数y1的表达式是y1=2x
B.两个函数图象的另一交点坐标为(4,-2)
C.正比例函数y1与反比例函数y2都随x的增大而增大
D.当x<-2或0
A.3 B.4 C.6 D.12
二、填空题(每小题4分,共32分)
8.把直线y=x+1向上平移3个单位得到的直线的函数表达式是 .
9.已知函数y=(m-2)是关于x的反比例函数,则m的值是 .
10.函数y=的自变量x的取值范围是 .
11.如图4,A是反比例函数y=的图象上任意一点,过点A分别作x轴,y轴的垂线,垂足为B,C,则四边形OBAC的面积为 .
图4
12.一个函数具有下列性质:①图象经过点(-1,2);②当x<0时,函数值y随自变量x的增大而增大.满足上述两条性质的函数表达式可以是 .(只要求写一个)
13.如图5,长方形ABCD的边AB与x轴平行,顶点A的坐标为(2,1),点B与点D都在反比例函数y=(x>0)的图象上,则长方形ABCD的周长为 .
图5 图6
14.如图6,点A的坐标可以看成是方程组 的解.
15.小明从家步行到学校需走的路程为2000米.图7中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分)的函数关系,根据图象提供的信息,当小明从家出发去学校步行20分钟时,距离学校还有 米.
图7
三、解答题(共40分)
16.(12分)在平面直角坐标系中,有一点M(a-1,2a+7),试求满足下列条件的a的值.
(1)点M在x轴上;
(2)点M在第二象限;
(3)点M到y轴的距离是1.
17.(13分)某超市预购进A,B两种品牌的T恤共200件,已知两种T恤的进价和售价如下表所示,设购进A种T恤x件,且所购进的两种T恤全部卖出,获得的总利润为W元.
品牌 进价(元/件) 售价(元/件)
A 50 80
B 40 65
(1)W关于x的函数表达式为 ;
(2)如果购进两种T恤的总费用不超过9500元,那么超市如何进货才能获得最大利润 求出最大利润.(提示:利润=售价-进价)
18.(15分)如图8所示,一次函数y=mx+n(m≠0)的图象与反比例函数y=(k≠0)的图象交于第二、四象限的点A(-2,a)和点B(b,-1),过点A作x轴的垂线,垂足为C,△AOC的面积为4.
(1)a= ,b= ;
(2)结合图象直接写出当mx+n>时x的取值范围为 ;
(3)在y轴上取点P,使PB-PA的值最大,求出点P的坐标.
图8
19 李师傅将容量为60升的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程s(千米)与行驶时间t(时)之间的关系如图所示(中途休息、加油的时间不计).当油箱中剩余油量为10升时,货车会自动显示加油提醒.设货车平均耗油量为0.1升/千米,请根据图象解答下列问题:
(1)直接写出工厂离目的地的路程;
(2)求s关于t的函数表达式;
(3)当货车显示加油提醒后,行驶时间t在怎样的范围内货车应进站加油
20某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍,用80元购买的甲食材比用20元购买的乙食材多1千克.
营养品信息表
营养成分 每千克含铁42毫克
配料表 原料 每千克含铁
甲食材 50毫克
乙食材 10毫克
规格 每包食材含量 每包单价
A包装 1千克 45元
B包装 0.25千克 12元
(1)甲、乙两种食材每千克进价分别是多少元
(2)该公司每日用18000元购进甲、乙两种食材并恰好全部用完.
①每日购进甲、乙两种食材各多少千克
②已知每日其他费用为2000元,且生产的营养品当日全部售出.若A的数量不低于B的数量,则A为多少包时,每日所获总利润最大,最大总利润为多少元
答案
1.D 2.D 3.B 4.C 5.D 6.D 7.A
8.y=x+4
9.-2
10.x≥-且x≠3 .
11.3
12.y=-(答案不唯一)
13.12 .
14.
15.240 .
16.解:(1)要使点M在x轴上,a应满足2a+7=0,解得a=-,
所以当a=-时,点M在x轴上.
(2)要使点M在第二象限,a应满足
解得-
17.解:(1)W=5x+5000 [解析] 购进A种T恤x件,则购进B种T恤(200-x)件.根据题意,得
W=(80-50)x+(65-40)(200-x)=30x+5000-25x=5x+5000.
(2)因为购进两种T恤的总费用不超过9500元,
所以50x+40(200-x)≤9500,解得x≤150.
因为W=5x+5000中,k=5>0,
所以W随x的增大而增大,
所以当x=150时,W的值最大,最大值为5750.
200-150=50(件).
所以当超市购进A种T恤150件,购进B种T恤50件时,才能获得最大利润,最大利润为5750元.
18.解:(1)4 8
(2)x<-2或0
如图,作点A关于y轴的对称点A',则A'(2,4),连结BA'并延长交y轴于点P,此时点P即为所求.
设直线A'B的表达式为y=cx+d(c≠0),则解得
所以直线A'B的表达式为y=-x+.
当x=0时,y=,
所以点P的坐标为0,.
19.解:(1)由图象,得t=0时,s=880,
所以工厂离目的地的路程为880千米.
(2)设s关于t的函数表达式为s=kt+b(k≠0),将(0,880)和(4,560)代入得
解得
所以s关于t的函数表达式为s=-80t+880(0≤t≤11).
(3)当油箱中剩余油量为10升时,s=880-(60-10)÷0.1=380(千米),
令380=-80t+880,解得t=;
当油箱中剩余油量为0升时,s=880-60÷0.1=280(千米),
令280=-80t+880,解得t=.
因为k=-80<0,所以s随t的增大而减小,
所以t的取值范围是
由题意得-=1,解得a=20.
经检验,a=20是所列方程的根,且符合题意,所以2a=40.
答:甲食材每千克进价为40元,乙食材每千克进价为20元.
(2)①设每日购进甲食材x千克,乙食材y千克,
由题意得
解得
答:每日购进甲食材400千克,乙食材100千克.
②设A为m包,则B为=(2000-4m)包.
因为A的数量不低于B的数量,
所以m≥2000-4m,所以m≥400.
设每日所获总利润为W元,根据题意得
W=45m+12(2000-4m)-18000-2000=-3m+4000.
因为k=-3<0,所以W随m的增大而减小,
所以当m=400时,W取最大值为2800.
答:当A为400包时,每日所获总利润最大,最大总利润为2800元.
