2021-2022学年冀教版九年级数学下册第30章二次函数 期末综合复习训练(Word版含解析)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学下册第30章二次函数 期末综合复习训练(Word版含解析) | 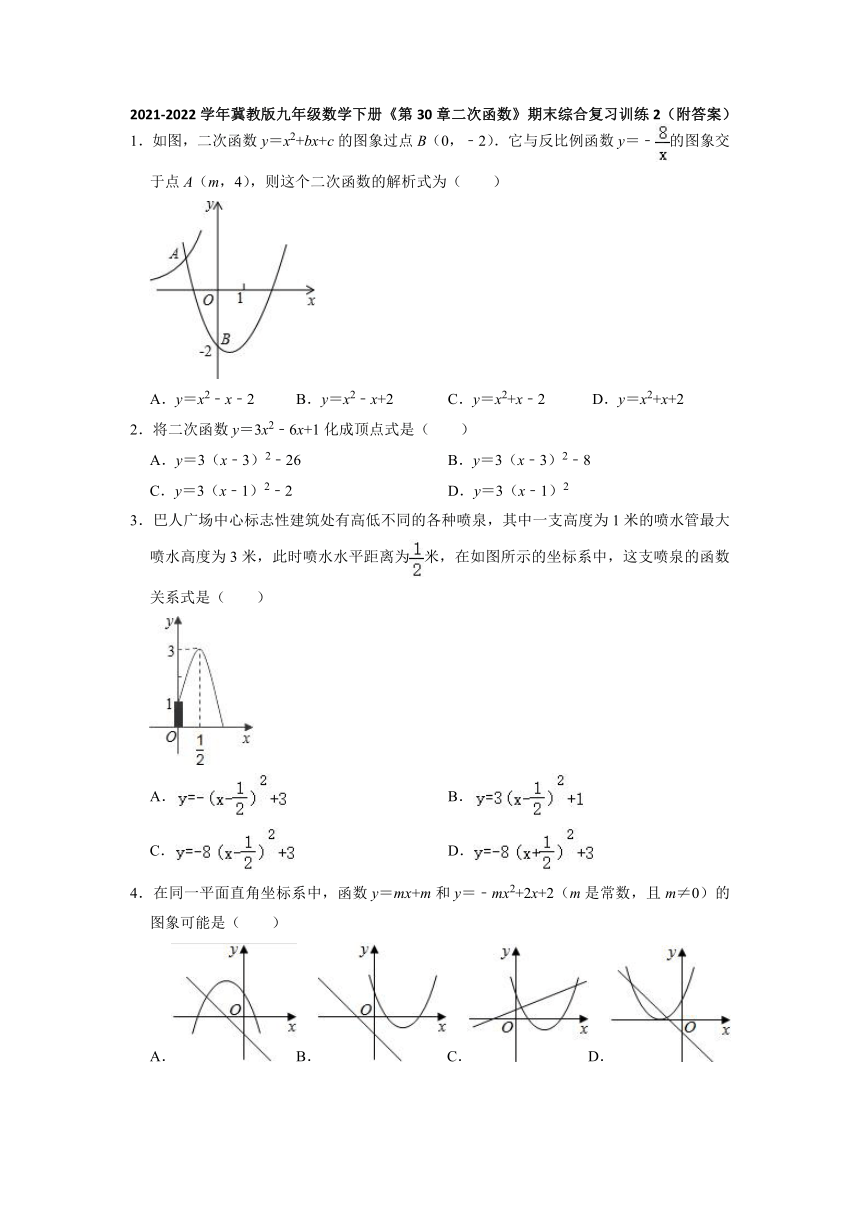 | |
| 格式 | doc | ||
| 文件大小 | 339.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 14:14:02 | ||
图片预览




文档简介
2021-2022学年冀教版九年级数学下册《第30章二次函数》期末综合复习训练2(附答案)
1.如图,二次函数y=x2+bx+c的图象过点B(0,﹣2).它与反比例函数y=﹣的图象交于点A(m,4),则这个二次函数的解析式为( )
A.y=x2﹣x﹣2 B.y=x2﹣x+2 C.y=x2+x﹣2 D.y=x2+x+2
2.将二次函数y=3x2﹣6x+1化成顶点式是( )
A.y=3(x﹣3)2﹣26 B.y=3(x﹣3)2﹣8
C.y=3(x﹣1)2﹣2 D.y=3(x﹣1)2
3.巴人广场中心标志性建筑处有高低不同的各种喷泉,其中一支高度为1米的喷水管最大喷水高度为3米,此时喷水水平距离为米,在如图所示的坐标系中,这支喷泉的函数关系式是( )
A. B.
C. D.
4.在同一平面直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.B.C.D.
5.给出下列四个命题:正确命题的个数是( )
(1)若点A在直线y=2x﹣3上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
(2)若A(a,m)、B(a﹣1,n)(a>0)在反比例函数y=的图象上,则m<n;
(3)一次函数y=﹣2x﹣3的图象不经过第三象限;
(4)二次函数y=﹣2x2﹣8x+1的最大值是9.
A.1个 B.2个 C.3个 D.4个
6.若A(﹣4,y1),B(﹣1,y2),C(2,y3)为二次函数y=﹣(x+2)2+3的图象上的三点,则y1,y2,y3的关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
7.如图,将抛物线y=﹣x2+x+5的图象x轴上方的部分沿x轴折到x轴下方,图象的其余部分不变,得到一个新图象.则新图象与直线y=﹣5的交点个数为( )
A.1 B.2 C.3 D.4
8.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ B.或 C.2或 D.2或或
9.如图是二次函数y=ax2+bx+c的图象,有下面四个结论:
①abc>0;②a﹣b+c>0;③2a+3b>0;④c﹣4b>0
其中,正确的结论是( )
A.①② B.①②③ C.①②④ D.①③④
10.在平面直角坐标系中,点P的坐标为(1,2),将抛物线y=x2﹣3x+2沿坐标轴平移一次,使其经过点P,则平移的最短距离为( )
A. B.1 C.5 D.
11.若抛物线y=2x2﹣px+4p+1中不管p取何值时都通过定点,则定点坐标为 .
12.把抛物线y=x2+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是y=x2﹣2x+1,则b= ,c= .
13.已知抛物线y=ax2﹣2ax+c与x轴一个交点的坐标为(﹣1,0),则一元二次方程ax2﹣2ax+c=0的根为 .
14.已知y=x2+mx﹣6,当1≤m≤3时,y<0恒成立,那么实数x的取值范围是 .
15.已知一次函数y1=kx+m和二次函数y2=ax2+bx+c的图象如图所示,它们的两个交点的横坐标是1和4,那么能够使得y1<y2的自变量x的取值范围是 .
16.用长度一定的绳子围成一个矩形,如果矩形的一边长x(m)与面积y(m2)满足函数关系y=﹣(x﹣12)2+144(0<x<24),则该矩形面积的最大值为 m2.
17.直角坐标系xOy中,O是坐标原点,抛物线y=x2﹣x﹣6与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.如果点M在y轴右侧的抛物线上,S△AMO=S△COB,那么点M的坐标是 .
18.二次函数y=x2+bx+c与直线y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②3b+c+6=0;③当x2+bx+c>1时,x<1;④当x2+bx+c>时,x>;⑤当1<x<3时,x2+(b﹣1)x+c<0.
其中正确结论的编号是 .
19.直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,那么不等式mx+n<ax2+bx+c<0的解集是 .
20.如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=﹣(x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .
21.已知,如图,抛物线y=ax2+bx+c经过点A(﹣1,0),B(0,﹣3),C(3,0 )三点.
(1)求抛物线的解析式;
(2)若抛物线的顶点为D,求sin∠BOD的值.
22.如图,经过点A(0,﹣6)的抛物线y=x2+bx+c与x轴相交于B(﹣2,0),C两点.
(1)求此抛物线的函数关系式和顶点D的坐标;
(2)将(1)中求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线y1,若新抛物线y1的顶点P在△ABC内,求m的取值范围;
(3)设点M在y轴上,∠OMB+∠OAB=∠ACB,直接写出AM的长.
23.如图,直线AB和抛物线的交点是A(0,﹣3),B(5,9),已知抛物线的顶点D的横坐标是2.
(1)求抛物线的解析式及顶点坐标;
(2)在x轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不在,请说明理由;
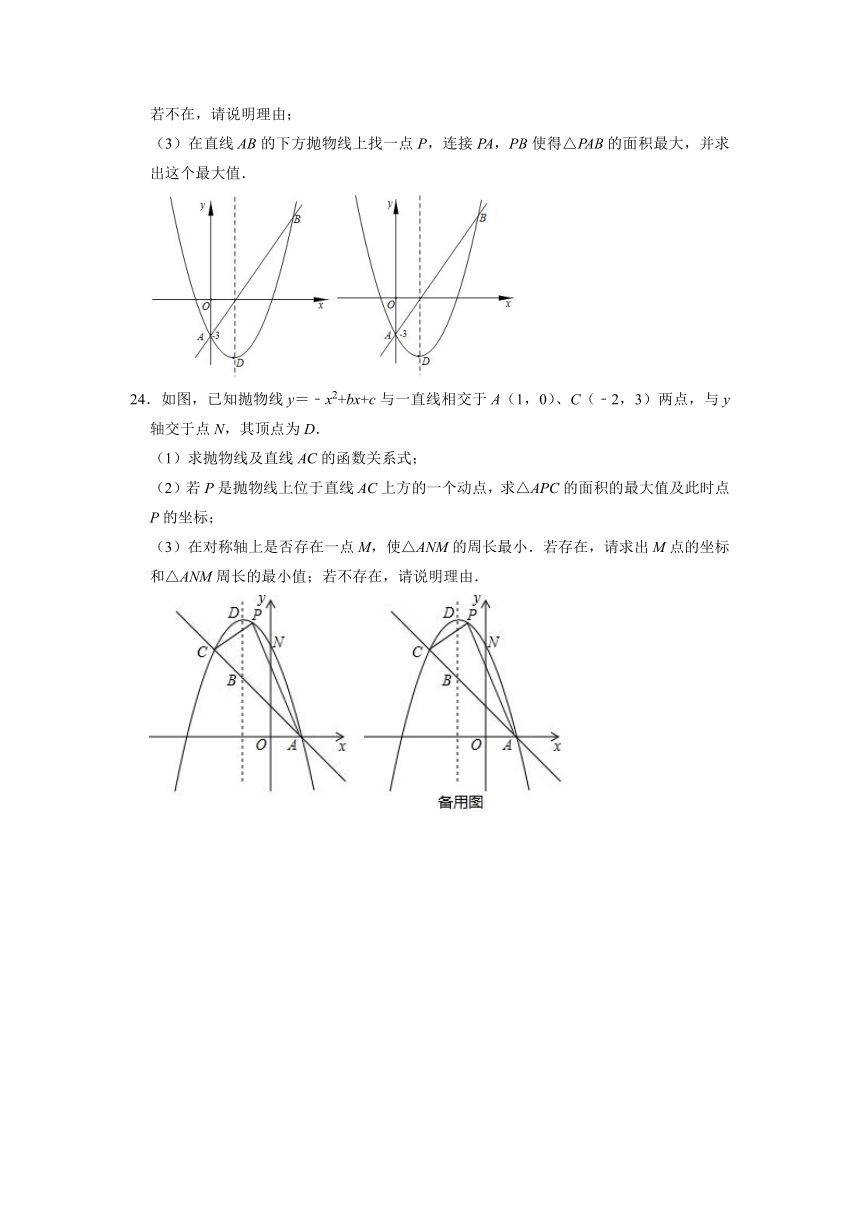
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
24.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.
参考答案
1.解:将A(m,4)代入反比例解析式得:4=﹣,即m=﹣2,
∴A(﹣2,4),
将A(﹣2,4),B(0,﹣2)代入二次函数解析式
得:,
解得:b=﹣1,c=﹣2,
则二次函数解析式为y=x2﹣x﹣2.
故选:A.
2.解:y=3x2﹣6x+1
=3(x2﹣2x)+1
=3(x﹣1)2﹣2.
故选:C.
3.解:根据图象知:
抛物线开口向下,顶点(,3),
∴答案B、D不符合.
把点(0,1)代入答案A、C检验,该点满足C.
故选:C.
4.解:解法一:逐项分析
A、由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B、由函数y=mx+m的图象可知m<0,二次函数的对称轴为x===<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C、由函数y=mx+m的图象可知m>0,即函数y=﹣mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D、由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,对称轴为x===<0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
解法二:当二次函数开口向下时,﹣m<0,m>0,
一次函数图象过一、二、三象限.
当二次函数开口向上时,﹣m>0,m<0,
对称轴x=<0,
这时二次函数图象的对称轴在y轴左侧,
一次函数图象过二、三、四象限.
故选:D.
5.解:(1)联立或,解得或
所以点A的坐标为(3,3)或(1,﹣1),在第一或第四象限正确
(2)反比例函数y=,在每个象限内y随x的增大而减小,点A在第一象限,而点B不能确定在第几象限,无法比较m、n的大小,错误
(3)一次函数y=﹣2x﹣3的图象不经过第一象限,错误
(4)二次函数y=﹣2x2﹣8x+1,可化为y=﹣2(x+2)2+9
所以二次函数y=﹣2x2﹣8x+1的最大值是9,正确.
(1)、(4)正确.
故选:B.
6.解:二次函数y=﹣(x+2)2+3的图象的开口向下(因为a=﹣1<0),对称轴是直线x=﹣2,
所以在对称轴的右侧,y随x的增大而减小,
点A关于对称轴对称的点的坐标为(0,y1),
∵﹣1<0<2,
∴y3<y1<y2,
故选:C.
7.解:如图,∵y=﹣x2+x+5中,当x=0时,y=5,
∴抛物线y=﹣x2+x+5与y轴的交点为(0,5),
∵将抛物线y=﹣x2+x+5图象中x轴上方的部分沿x轴翻折到x轴下方,图象的其余部分不变,
∴新图象与y轴的交点坐标为(0,﹣5),
∴新图象与直线y=﹣5的交点个数是4个,
故选:D.
8.解:二次函数的对称轴为直线x=m,
①m<﹣2时,x=﹣2时二次函数有最大值,
此时﹣(﹣2﹣m)2+m2+1=4,
解得m=﹣,与m<﹣2矛盾,故m值不存在;
②当﹣2≤m≤1时,x=m时,二次函数有最大值,
此时,m2+1=4,
解得m=﹣,m=(舍去);
③当m>1时,x=1时二次函数有最大值,
此时,﹣(1﹣m)2+m2+1=4,
解得m=2,
综上所述,m的值为2或﹣.
故选:C.
9.解:∵抛物线开口向上,
∴a>0;
∵抛物线的对称轴在y轴的右侧,
∴x=﹣>0,
∴b<0;
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以①正确;
∵x=﹣1时,y>0,
∴a﹣b+c>0,所以②正确;
∵x=﹣=,
∴2a+3b=0,所以③错误;
∵x=2时,y>0,
∴4a+2b+c>0,
把2a=﹣3b代入得﹣6b+2b+c>0,
∴c﹣4b>0,所以④正确.
故选:C.
10.解:y=x2﹣3x+2=(x﹣3)2﹣,
当沿水平方向平移时,纵坐标和P的纵坐标相同,把y=2代入y=x2﹣3x+2得:2=x2﹣3x+2,
解得:x=0或6,
平移的最短距离是1﹣0=1,
当沿竖直方向平移时,横坐标和P的横坐标相同,把x=1代入y=x2﹣3x+2得:y=×12﹣3×1+2=﹣,
平移的最短距离是2+=,
即平移的最短距离是1,
故选:B.
11.解:y=2x2﹣px+4p+1可化为y=2x2﹣p(x﹣4)+1,
分析可得:当x=4时,y=33;且与p的取值无关;
故不管p取何值时都通过定点(4,33).
12.解:∵y=x2﹣2x+1=(x﹣1)2,
∴抛物线顶点坐标为(1,0),
依题意,得平移前抛物线顶点坐标为(﹣2,2),
∵平移不改变二次项系数,
∴y=(x+2)2+2=x2+4x+6,
比较系数,得b=4,c=6.
故本题答案为:4,6.
13.解法一:将x=﹣1,y=0代入y=ax2﹣2ax+c得:a+2a+c=0.
解得:c=﹣3a.
将c=﹣3a代入方程得:ax2﹣2ax﹣3a=0.
∴a(x2﹣2x﹣3)=0.
∴a(x+1)(x﹣3)=0.
∴x1=﹣1,x2=3.
解法二:已知抛物线的对称轴为x==1,又抛物线与x轴一个交点的坐标为(﹣1,0),则根据对称性可知另一个交点坐标为(3,0);故而ax2﹣2ax+c=0的两个根为﹣1,3
故答案为:﹣1,3.
14.解:∵1≤m≤3,y<0,
∴当m=3时,x2+3x﹣6<0,
由y=x2+3x﹣6<0,
得<x<;
当m=1时,x2+x﹣6<0,
由y=x2+x﹣6<0,得﹣3<x<2.
∴实数x的取值范围为:﹣3<x<.
故答案为:﹣3<x<.
15.解:依题意得,能够使得y1<y2的自变量x的取值范围,
实质上就是根据图象找出函数y1=kx+m的值小于y2=ax2+bx+c的值时x的取值范围,
由两个函数图象的交点横坐标及图象的位置可以知道此时x的取值范围x>4或x<1.
故填空答案:x>4或x<1.
16.解:由函数关系y=﹣(x﹣12)2+144(0<x<24)可知,
∵二次函数的二次项系数即﹣1<0,
∴当x=12时,y最大值=144.
17.解:在抛物线y=x2﹣x﹣6中,
当y=0时,x=﹣2或3,
即A(﹣2,0),B(3,0);
当x=0时,y=﹣6,
即C(0,﹣6);
故S△COB=9,
设点M的纵坐标为y,必有×AO |y|=9,
解可得y=±9,
将其代入解析式可得x的值为,(舍去),
故点M的坐标是(,9).
18.解:∵函数y=x2+bx+c与x轴无交点,
∴b2﹣4ac<0;
∴b2﹣4c<0
故①不正确;
当x=3时,y=9+3b+c=3,
∴3b+c+6=0
故②正确;
从图象可知当x2+bx+c>1时,x<1或x>2
③不正确;
④过顶点(,)的反比例函数为y=,
由图象可知,当x2+bx+c>时,x>或x<0,
④错误.
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b﹣1)x+c<0.
故⑤正确.
故答案为:②⑤
19.解:因为mx+n<ax2+bx+c<0,由图可知,1<x<2.
20.方法一:
解:由题意可得出:y=a(x+6)2+4,
将(﹣12,0)代入得出,0=a(﹣12+6)2+4,
解得:a=﹣,
∴选取点B为坐标原点时的抛物线解析式是:y=﹣(x+6)2+4.
故答案为:y=﹣(x+6)2+4.
方法二:B为原点相当于把原函数左移12个单位,也由顶点坐标(6,4)变为(﹣6,4),
故点B为坐标原点时的抛物线解析式是:y=﹣(x+6)2+4.
21.解:(1)由已知得解得.
所以,抛物线的解析式为y=x2﹣2x﹣3.
(2)过D作DE⊥y轴于点E.
抛物线的解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,
则物线的顶点坐标为(1,﹣4),则OE=4,DE=1.
在直角△ODE中,根据勾股定理即可得到:OD===.
则sin∠BOD==.
22.解:(1)将A(0,﹣6)、B(﹣2,0)代入抛物线y=x2+bx+c中,得:
,
解得.
∴抛物线的解析式:y=x2﹣2x﹣6=(x﹣2)2﹣8,顶点D(2,﹣8);
(2)由题意,新抛物线的解析式可表示为:y=(x﹣2+1)2﹣8+m,
即:y=(x﹣2+1)2﹣8+m.它的顶点坐标P(1,m﹣8).
由(1)的抛物线解析式可得:C(6,0).
∴直线AB:y=﹣3x﹣6;直线AC:y=x﹣6.
当点P在直线AC上时,1﹣6=m﹣8,解得:m=3;
在x轴上时m=8,则m取值范围为3<m<8.
(3)由A(0,﹣6)、C(6,0)得:OA=OC=6,且△OAC是等腰直角三角形.
如图,在OA上取ON=OB=2,则∠ONB=∠ACB=45°.
∴∠ONB=∠NBA+∠OAB=∠ACB=∠OMB+∠OAB,
即∠NBA=∠OMB.
如图,在△ABN、△AM1B中,
∠BAN=∠M1AB,∠ABN=∠AM1B,
∴△ABN∽△AM1B,得:AB2=AN AM1;
由勾股定理,得AB2=(﹣2)2+(﹣6)2=40,
又∵AN=OA﹣ON=6﹣2=4,
∴AM1=40÷4=10,
OM1=AM1﹣OA=10﹣6=4
OM2=OM1=4
AM2=OA﹣OM2=6﹣4=2.
综上所述,AM的长为10或2.
23.解:(1)抛物线的顶点D的横坐标是2,则x=﹣=2…①,
抛物线过是A(0,﹣3),则:函数的表达式为:y=ax2+bx﹣3,
把B点坐标代入上式得:9=25a+5b﹣3…②,
联立①、②解得:a=,b=﹣,c=﹣3,
∴抛物线的解析式为:y=x2﹣x﹣3,
当x=2时,y=﹣,即顶点D的坐标为(2,﹣);
(2)A(0,﹣3),B(5,9),则AB=13,
①当AB=AC时,设点C坐标(m,0),
则:(m)2+(﹣3)2=132,解得:m=±4,
即点C坐标为:(4,0)或(﹣4,0);
②当AB=BC时,设点C坐标(m,0),
则:(5﹣m)2+92=132,解得:m=5,
即:点C坐标为(5,0)或(5﹣2,0),
③当AC=BC时,设点C坐标(m,0),
则:点C为AB的垂直平分线于x轴的交点,
则点C坐标为(,0),
故:存在,
点C的坐标为:(4,0)或(﹣4,0)或(5,0)或(5﹣2,0)或(,0);
(3)过点P作y轴的平行线交AB于点H,
设:AB所在的直线过点A(0,﹣3),则设直线AB的表达式为y=kx﹣3,
把点B坐标代入上式,9=5k﹣3,则k=,
故函数的表达式为:y=x﹣3,
设:点P坐标为(m,m2﹣m﹣3),则点H坐标为(m,m﹣3),
S△PAB= PH xB=(﹣m2+12m),
当m=2.5时,S△PAB取得最大值为:,
答:△PAB的面积最大值为.
24.解:(1)将A(1,0),C(﹣2,3)代入y=﹣x2+bx+c,得:
,解得:,
∴抛物线的函数关系式为y=﹣x2﹣2x+3;
设直线AC的函数关系式为y=mx+n(m≠0),
将A(1,0),C(﹣2,3)代入y=mx+n,得:
,解得:,
∴直线AC的函数关系式为y=﹣x+1.
(2)过点P作PE∥y轴交x轴于点E,交直线AC于点F,过点C作CQ∥y轴交x轴于点Q,如图1所示.
设点P的坐标为(x,﹣x2﹣2x+3)(﹣2<x<1),则点E的坐标为(x,0),点F的坐标为(x,﹣x+1),
∴PE=﹣x2﹣2x+3,EF=﹣x+1,
PF=PE﹣EF=﹣x2﹣2x+3﹣(﹣x+1)=﹣x2﹣x+2.
∵点C的坐标为(﹣2,3),
∴点Q的坐标为(﹣2,0),
∴AQ=1﹣(﹣2)=3,
∴S△APC=AQ PF=﹣x2﹣x+3=﹣(x+)2+.
∵﹣<0,
∴当x=﹣时,△APC的面积取最大值,最大值为,此时点P的坐标为(﹣,).
(3)当x=0时,y=﹣x2﹣2x+3=3,
∴点N的坐标为(0,3).
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线的对称轴为直线x=﹣1.
∵点C的坐标为(﹣2,3),
∴点C,N关于抛物线的对称轴对称.
令直线AC与抛物线的对称轴的交点为点M,如图2所示.
∵点C,N关于抛物线的对称轴对称,
∴MN=CM,
∴AM+MN=AM+MC=AC,
∴此时△ANM周长取最小值.
当x=﹣1时,y=﹣x+1=2,
∴此时点M的坐标为(﹣1,2).
∵点A的坐标为(1,0),点C的坐标为(﹣2,3),点N的坐标为(0,3),
∴AC==3,AN==,
∴C△ANM=AM+MN+AN=AC+AN=3+.
∴在对称轴上存在一点M(﹣1,2),使△ANM的周长最小,△ANM周长的最小值为3+.
1.如图,二次函数y=x2+bx+c的图象过点B(0,﹣2).它与反比例函数y=﹣的图象交于点A(m,4),则这个二次函数的解析式为( )
A.y=x2﹣x﹣2 B.y=x2﹣x+2 C.y=x2+x﹣2 D.y=x2+x+2
2.将二次函数y=3x2﹣6x+1化成顶点式是( )
A.y=3(x﹣3)2﹣26 B.y=3(x﹣3)2﹣8
C.y=3(x﹣1)2﹣2 D.y=3(x﹣1)2
3.巴人广场中心标志性建筑处有高低不同的各种喷泉,其中一支高度为1米的喷水管最大喷水高度为3米,此时喷水水平距离为米,在如图所示的坐标系中,这支喷泉的函数关系式是( )
A. B.
C. D.
4.在同一平面直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.B.C.D.
5.给出下列四个命题:正确命题的个数是( )
(1)若点A在直线y=2x﹣3上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
(2)若A(a,m)、B(a﹣1,n)(a>0)在反比例函数y=的图象上,则m<n;
(3)一次函数y=﹣2x﹣3的图象不经过第三象限;
(4)二次函数y=﹣2x2﹣8x+1的最大值是9.
A.1个 B.2个 C.3个 D.4个
6.若A(﹣4,y1),B(﹣1,y2),C(2,y3)为二次函数y=﹣(x+2)2+3的图象上的三点,则y1,y2,y3的关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
7.如图,将抛物线y=﹣x2+x+5的图象x轴上方的部分沿x轴折到x轴下方,图象的其余部分不变,得到一个新图象.则新图象与直线y=﹣5的交点个数为( )
A.1 B.2 C.3 D.4
8.当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( )
A.﹣ B.或 C.2或 D.2或或
9.如图是二次函数y=ax2+bx+c的图象,有下面四个结论:
①abc>0;②a﹣b+c>0;③2a+3b>0;④c﹣4b>0
其中,正确的结论是( )
A.①② B.①②③ C.①②④ D.①③④
10.在平面直角坐标系中,点P的坐标为(1,2),将抛物线y=x2﹣3x+2沿坐标轴平移一次,使其经过点P,则平移的最短距离为( )
A. B.1 C.5 D.
11.若抛物线y=2x2﹣px+4p+1中不管p取何值时都通过定点,则定点坐标为 .
12.把抛物线y=x2+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是y=x2﹣2x+1,则b= ,c= .
13.已知抛物线y=ax2﹣2ax+c与x轴一个交点的坐标为(﹣1,0),则一元二次方程ax2﹣2ax+c=0的根为 .
14.已知y=x2+mx﹣6,当1≤m≤3时,y<0恒成立,那么实数x的取值范围是 .
15.已知一次函数y1=kx+m和二次函数y2=ax2+bx+c的图象如图所示,它们的两个交点的横坐标是1和4,那么能够使得y1<y2的自变量x的取值范围是 .
16.用长度一定的绳子围成一个矩形,如果矩形的一边长x(m)与面积y(m2)满足函数关系y=﹣(x﹣12)2+144(0<x<24),则该矩形面积的最大值为 m2.
17.直角坐标系xOy中,O是坐标原点,抛物线y=x2﹣x﹣6与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.如果点M在y轴右侧的抛物线上,S△AMO=S△COB,那么点M的坐标是 .
18.二次函数y=x2+bx+c与直线y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②3b+c+6=0;③当x2+bx+c>1时,x<1;④当x2+bx+c>时,x>;⑤当1<x<3时,x2+(b﹣1)x+c<0.
其中正确结论的编号是 .
19.直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,那么不等式mx+n<ax2+bx+c<0的解集是 .
20.如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=﹣(x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .
21.已知,如图,抛物线y=ax2+bx+c经过点A(﹣1,0),B(0,﹣3),C(3,0 )三点.
(1)求抛物线的解析式;
(2)若抛物线的顶点为D,求sin∠BOD的值.
22.如图,经过点A(0,﹣6)的抛物线y=x2+bx+c与x轴相交于B(﹣2,0),C两点.
(1)求此抛物线的函数关系式和顶点D的坐标;
(2)将(1)中求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线y1,若新抛物线y1的顶点P在△ABC内,求m的取值范围;
(3)设点M在y轴上,∠OMB+∠OAB=∠ACB,直接写出AM的长.
23.如图,直线AB和抛物线的交点是A(0,﹣3),B(5,9),已知抛物线的顶点D的横坐标是2.
(1)求抛物线的解析式及顶点坐标;
(2)在x轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
24.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.
参考答案
1.解:将A(m,4)代入反比例解析式得:4=﹣,即m=﹣2,
∴A(﹣2,4),
将A(﹣2,4),B(0,﹣2)代入二次函数解析式
得:,
解得:b=﹣1,c=﹣2,
则二次函数解析式为y=x2﹣x﹣2.
故选:A.
2.解:y=3x2﹣6x+1
=3(x2﹣2x)+1
=3(x﹣1)2﹣2.
故选:C.
3.解:根据图象知:
抛物线开口向下,顶点(,3),
∴答案B、D不符合.
把点(0,1)代入答案A、C检验,该点满足C.
故选:C.
4.解:解法一:逐项分析
A、由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B、由函数y=mx+m的图象可知m<0,二次函数的对称轴为x===<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C、由函数y=mx+m的图象可知m>0,即函数y=﹣mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D、由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,对称轴为x===<0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
解法二:当二次函数开口向下时,﹣m<0,m>0,
一次函数图象过一、二、三象限.
当二次函数开口向上时,﹣m>0,m<0,
对称轴x=<0,
这时二次函数图象的对称轴在y轴左侧,
一次函数图象过二、三、四象限.
故选:D.
5.解:(1)联立或,解得或
所以点A的坐标为(3,3)或(1,﹣1),在第一或第四象限正确
(2)反比例函数y=,在每个象限内y随x的增大而减小,点A在第一象限,而点B不能确定在第几象限,无法比较m、n的大小,错误
(3)一次函数y=﹣2x﹣3的图象不经过第一象限,错误
(4)二次函数y=﹣2x2﹣8x+1,可化为y=﹣2(x+2)2+9
所以二次函数y=﹣2x2﹣8x+1的最大值是9,正确.
(1)、(4)正确.
故选:B.
6.解:二次函数y=﹣(x+2)2+3的图象的开口向下(因为a=﹣1<0),对称轴是直线x=﹣2,
所以在对称轴的右侧,y随x的增大而减小,
点A关于对称轴对称的点的坐标为(0,y1),
∵﹣1<0<2,
∴y3<y1<y2,
故选:C.
7.解:如图,∵y=﹣x2+x+5中,当x=0时,y=5,
∴抛物线y=﹣x2+x+5与y轴的交点为(0,5),
∵将抛物线y=﹣x2+x+5图象中x轴上方的部分沿x轴翻折到x轴下方,图象的其余部分不变,
∴新图象与y轴的交点坐标为(0,﹣5),
∴新图象与直线y=﹣5的交点个数是4个,
故选:D.
8.解:二次函数的对称轴为直线x=m,
①m<﹣2时,x=﹣2时二次函数有最大值,
此时﹣(﹣2﹣m)2+m2+1=4,
解得m=﹣,与m<﹣2矛盾,故m值不存在;
②当﹣2≤m≤1时,x=m时,二次函数有最大值,
此时,m2+1=4,
解得m=﹣,m=(舍去);
③当m>1时,x=1时二次函数有最大值,
此时,﹣(1﹣m)2+m2+1=4,
解得m=2,
综上所述,m的值为2或﹣.
故选:C.
9.解:∵抛物线开口向上,
∴a>0;
∵抛物线的对称轴在y轴的右侧,
∴x=﹣>0,
∴b<0;
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以①正确;
∵x=﹣1时,y>0,
∴a﹣b+c>0,所以②正确;
∵x=﹣=,
∴2a+3b=0,所以③错误;
∵x=2时,y>0,
∴4a+2b+c>0,
把2a=﹣3b代入得﹣6b+2b+c>0,
∴c﹣4b>0,所以④正确.
故选:C.
10.解:y=x2﹣3x+2=(x﹣3)2﹣,
当沿水平方向平移时,纵坐标和P的纵坐标相同,把y=2代入y=x2﹣3x+2得:2=x2﹣3x+2,
解得:x=0或6,
平移的最短距离是1﹣0=1,
当沿竖直方向平移时,横坐标和P的横坐标相同,把x=1代入y=x2﹣3x+2得:y=×12﹣3×1+2=﹣,
平移的最短距离是2+=,
即平移的最短距离是1,
故选:B.
11.解:y=2x2﹣px+4p+1可化为y=2x2﹣p(x﹣4)+1,
分析可得:当x=4时,y=33;且与p的取值无关;
故不管p取何值时都通过定点(4,33).
12.解:∵y=x2﹣2x+1=(x﹣1)2,
∴抛物线顶点坐标为(1,0),
依题意,得平移前抛物线顶点坐标为(﹣2,2),
∵平移不改变二次项系数,
∴y=(x+2)2+2=x2+4x+6,
比较系数,得b=4,c=6.
故本题答案为:4,6.
13.解法一:将x=﹣1,y=0代入y=ax2﹣2ax+c得:a+2a+c=0.
解得:c=﹣3a.
将c=﹣3a代入方程得:ax2﹣2ax﹣3a=0.
∴a(x2﹣2x﹣3)=0.
∴a(x+1)(x﹣3)=0.
∴x1=﹣1,x2=3.
解法二:已知抛物线的对称轴为x==1,又抛物线与x轴一个交点的坐标为(﹣1,0),则根据对称性可知另一个交点坐标为(3,0);故而ax2﹣2ax+c=0的两个根为﹣1,3
故答案为:﹣1,3.
14.解:∵1≤m≤3,y<0,
∴当m=3时,x2+3x﹣6<0,
由y=x2+3x﹣6<0,
得<x<;
当m=1时,x2+x﹣6<0,
由y=x2+x﹣6<0,得﹣3<x<2.
∴实数x的取值范围为:﹣3<x<.
故答案为:﹣3<x<.
15.解:依题意得,能够使得y1<y2的自变量x的取值范围,
实质上就是根据图象找出函数y1=kx+m的值小于y2=ax2+bx+c的值时x的取值范围,
由两个函数图象的交点横坐标及图象的位置可以知道此时x的取值范围x>4或x<1.
故填空答案:x>4或x<1.
16.解:由函数关系y=﹣(x﹣12)2+144(0<x<24)可知,
∵二次函数的二次项系数即﹣1<0,
∴当x=12时,y最大值=144.
17.解:在抛物线y=x2﹣x﹣6中,
当y=0时,x=﹣2或3,
即A(﹣2,0),B(3,0);
当x=0时,y=﹣6,
即C(0,﹣6);
故S△COB=9,
设点M的纵坐标为y,必有×AO |y|=9,
解可得y=±9,
将其代入解析式可得x的值为,(舍去),
故点M的坐标是(,9).
18.解:∵函数y=x2+bx+c与x轴无交点,
∴b2﹣4ac<0;
∴b2﹣4c<0
故①不正确;
当x=3时,y=9+3b+c=3,
∴3b+c+6=0
故②正确;
从图象可知当x2+bx+c>1时,x<1或x>2
③不正确;
④过顶点(,)的反比例函数为y=,
由图象可知,当x2+bx+c>时,x>或x<0,
④错误.
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b﹣1)x+c<0.
故⑤正确.
故答案为:②⑤
19.解:因为mx+n<ax2+bx+c<0,由图可知,1<x<2.
20.方法一:
解:由题意可得出:y=a(x+6)2+4,
将(﹣12,0)代入得出,0=a(﹣12+6)2+4,
解得:a=﹣,
∴选取点B为坐标原点时的抛物线解析式是:y=﹣(x+6)2+4.
故答案为:y=﹣(x+6)2+4.
方法二:B为原点相当于把原函数左移12个单位,也由顶点坐标(6,4)变为(﹣6,4),
故点B为坐标原点时的抛物线解析式是:y=﹣(x+6)2+4.
21.解:(1)由已知得解得.
所以,抛物线的解析式为y=x2﹣2x﹣3.
(2)过D作DE⊥y轴于点E.
抛物线的解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,
则物线的顶点坐标为(1,﹣4),则OE=4,DE=1.
在直角△ODE中,根据勾股定理即可得到:OD===.
则sin∠BOD==.
22.解:(1)将A(0,﹣6)、B(﹣2,0)代入抛物线y=x2+bx+c中,得:
,
解得.
∴抛物线的解析式:y=x2﹣2x﹣6=(x﹣2)2﹣8,顶点D(2,﹣8);
(2)由题意,新抛物线的解析式可表示为:y=(x﹣2+1)2﹣8+m,
即:y=(x﹣2+1)2﹣8+m.它的顶点坐标P(1,m﹣8).
由(1)的抛物线解析式可得:C(6,0).
∴直线AB:y=﹣3x﹣6;直线AC:y=x﹣6.
当点P在直线AC上时,1﹣6=m﹣8,解得:m=3;
在x轴上时m=8,则m取值范围为3<m<8.
(3)由A(0,﹣6)、C(6,0)得:OA=OC=6,且△OAC是等腰直角三角形.
如图,在OA上取ON=OB=2,则∠ONB=∠ACB=45°.
∴∠ONB=∠NBA+∠OAB=∠ACB=∠OMB+∠OAB,
即∠NBA=∠OMB.
如图,在△ABN、△AM1B中,
∠BAN=∠M1AB,∠ABN=∠AM1B,
∴△ABN∽△AM1B,得:AB2=AN AM1;
由勾股定理,得AB2=(﹣2)2+(﹣6)2=40,
又∵AN=OA﹣ON=6﹣2=4,
∴AM1=40÷4=10,
OM1=AM1﹣OA=10﹣6=4
OM2=OM1=4
AM2=OA﹣OM2=6﹣4=2.
综上所述,AM的长为10或2.
23.解:(1)抛物线的顶点D的横坐标是2,则x=﹣=2…①,
抛物线过是A(0,﹣3),则:函数的表达式为:y=ax2+bx﹣3,
把B点坐标代入上式得:9=25a+5b﹣3…②,
联立①、②解得:a=,b=﹣,c=﹣3,
∴抛物线的解析式为:y=x2﹣x﹣3,
当x=2时,y=﹣,即顶点D的坐标为(2,﹣);
(2)A(0,﹣3),B(5,9),则AB=13,
①当AB=AC时,设点C坐标(m,0),
则:(m)2+(﹣3)2=132,解得:m=±4,
即点C坐标为:(4,0)或(﹣4,0);
②当AB=BC时,设点C坐标(m,0),
则:(5﹣m)2+92=132,解得:m=5,
即:点C坐标为(5,0)或(5﹣2,0),
③当AC=BC时,设点C坐标(m,0),
则:点C为AB的垂直平分线于x轴的交点,
则点C坐标为(,0),
故:存在,
点C的坐标为:(4,0)或(﹣4,0)或(5,0)或(5﹣2,0)或(,0);
(3)过点P作y轴的平行线交AB于点H,
设:AB所在的直线过点A(0,﹣3),则设直线AB的表达式为y=kx﹣3,
把点B坐标代入上式,9=5k﹣3,则k=,
故函数的表达式为:y=x﹣3,
设:点P坐标为(m,m2﹣m﹣3),则点H坐标为(m,m﹣3),
S△PAB= PH xB=(﹣m2+12m),
当m=2.5时,S△PAB取得最大值为:,
答:△PAB的面积最大值为.
24.解:(1)将A(1,0),C(﹣2,3)代入y=﹣x2+bx+c,得:
,解得:,
∴抛物线的函数关系式为y=﹣x2﹣2x+3;
设直线AC的函数关系式为y=mx+n(m≠0),
将A(1,0),C(﹣2,3)代入y=mx+n,得:
,解得:,
∴直线AC的函数关系式为y=﹣x+1.
(2)过点P作PE∥y轴交x轴于点E,交直线AC于点F,过点C作CQ∥y轴交x轴于点Q,如图1所示.
设点P的坐标为(x,﹣x2﹣2x+3)(﹣2<x<1),则点E的坐标为(x,0),点F的坐标为(x,﹣x+1),
∴PE=﹣x2﹣2x+3,EF=﹣x+1,
PF=PE﹣EF=﹣x2﹣2x+3﹣(﹣x+1)=﹣x2﹣x+2.
∵点C的坐标为(﹣2,3),
∴点Q的坐标为(﹣2,0),
∴AQ=1﹣(﹣2)=3,
∴S△APC=AQ PF=﹣x2﹣x+3=﹣(x+)2+.
∵﹣<0,
∴当x=﹣时,△APC的面积取最大值,最大值为,此时点P的坐标为(﹣,).
(3)当x=0时,y=﹣x2﹣2x+3=3,
∴点N的坐标为(0,3).
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线的对称轴为直线x=﹣1.
∵点C的坐标为(﹣2,3),
∴点C,N关于抛物线的对称轴对称.
令直线AC与抛物线的对称轴的交点为点M,如图2所示.
∵点C,N关于抛物线的对称轴对称,
∴MN=CM,
∴AM+MN=AM+MC=AC,
∴此时△ANM周长取最小值.
当x=﹣1时,y=﹣x+1=2,
∴此时点M的坐标为(﹣1,2).
∵点A的坐标为(1,0),点C的坐标为(﹣2,3),点N的坐标为(0,3),
∴AC==3,AN==,
∴C△ANM=AM+MN+AN=AC+AN=3+.
∴在对称轴上存在一点M(﹣1,2),使△ANM的周长最小,△ANM周长的最小值为3+.
