沪科版数学九年级上册 23.1 锐角的三角函数 课件(共14张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 23.1 锐角的三角函数 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 147.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 12:45:40 | ||
图片预览





文档简介
(共14张PPT)
23.1 锐角的三角函数
23 解直角三角形复习课
三角函数
一、基本定义:
你觉得运用时应该注意什么
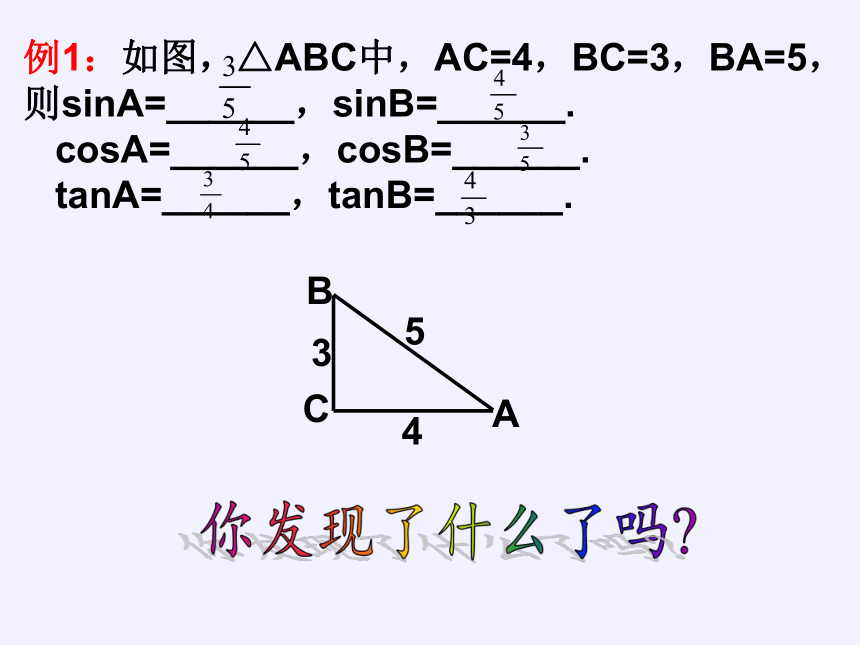
例1:如图,△ABC中,AC=4,BC=3,BA=5,则sinA=______,sinB=______.
cosA=______,cosB=______.
tanA=______,tanB=______.
你发现了什么了吗
A
C
B
3
4
5
练习1、如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,AB=7,AC=3,则sin∠BCD=_____.
练习2、Rt△ABC中,∠C=900 ,
求tanB,cosA
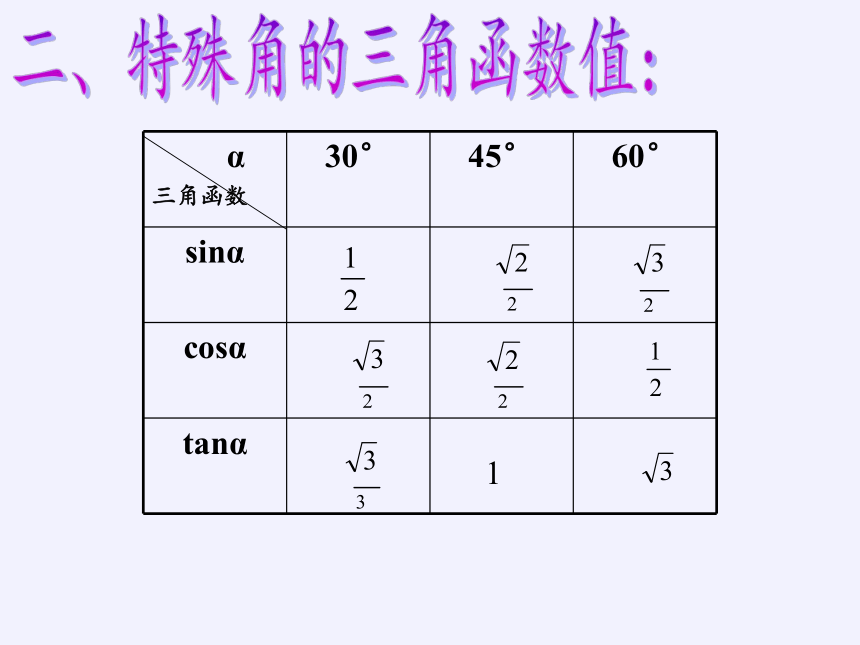
二、特殊角的三角函数值:
α 三角函数 30° 45° 60°
sinα
cosα
tanα
正切值随着锐角的度数的增大而_____;
正弦值随着锐角的度数的增大而_____;
余弦值随着锐角的度数的增大而_____.
增大
增大
减小
三、三角函数的增减性:
异名函数化为同名函数
练习1、比较大小:
(1)sin250____sin430 (2)cos70____cos80
(3)sin480____cos520 (4)tan480____tan400
练习2、已知:300<α<450,则:
(1)sin α的取值范围:________;
(2)cosα的取值范围:________;
(3)tanα的取值范围:________.
例1、计算:
例2、已知△ABC满足
则△ABC是______三角形.
1、在直角三角形中,利用已知的元素求出所有未知元素的过程,叫解直角三角形.
2、知道直角三角形中的2个元素(至少有一边),可以求出其它三个元素.
四、解直角三角形:
例2、如图,在△ABC中,∠A=30°,tanB= AC= ,求AB的长.
A
B
C
例1、在Rt△ABC中,∠C=90°,∠A=60°,a-b= ,解这个直角三角形.
D
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系 a2+b2=c 2 勾股定理
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
课堂小结
五.作业设置:课本136页第8题第9题。
谢 谢
23.1 锐角的三角函数
23 解直角三角形复习课
三角函数
一、基本定义:
你觉得运用时应该注意什么
例1:如图,△ABC中,AC=4,BC=3,BA=5,则sinA=______,sinB=______.
cosA=______,cosB=______.
tanA=______,tanB=______.
你发现了什么了吗
A
C
B
3
4
5
练习1、如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,AB=7,AC=3,则sin∠BCD=_____.
练习2、Rt△ABC中,∠C=900 ,
求tanB,cosA
二、特殊角的三角函数值:
α 三角函数 30° 45° 60°
sinα
cosα
tanα
正切值随着锐角的度数的增大而_____;
正弦值随着锐角的度数的增大而_____;
余弦值随着锐角的度数的增大而_____.
增大
增大
减小
三、三角函数的增减性:
异名函数化为同名函数
练习1、比较大小:
(1)sin250____sin430 (2)cos70____cos80
(3)sin480____cos520 (4)tan480____tan400
练习2、已知:300<α<450,则:
(1)sin α的取值范围:________;
(2)cosα的取值范围:________;
(3)tanα的取值范围:________.
例1、计算:
例2、已知△ABC满足
则△ABC是______三角形.
1、在直角三角形中,利用已知的元素求出所有未知元素的过程,叫解直角三角形.
2、知道直角三角形中的2个元素(至少有一边),可以求出其它三个元素.
四、解直角三角形:
例2、如图,在△ABC中,∠A=30°,tanB= AC= ,求AB的长.
A
B
C
例1、在Rt△ABC中,∠C=90°,∠A=60°,a-b= ,解这个直角三角形.
D
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系 a2+b2=c 2 勾股定理
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到下面一些关系:
课堂小结
五.作业设置:课本136页第8题第9题。
谢 谢
