沪科版数学九年级上册 22.1 相似三角形 课件(共18张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 22.1 相似三角形 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 12:53:55 | ||
图片预览


文档简介
(共18张PPT)
△ABC∽△A/B/C/,如果BC=3,B/C/=1.5,那么△A/B/C/
与 △ABC的相似比为_________.
1.相似三角形的定义:
对应角相等、对应边成比例的三角形叫做相似三角形。
2.相似比:
相似三角形的对应边的比,叫做相似三角形的相似比。
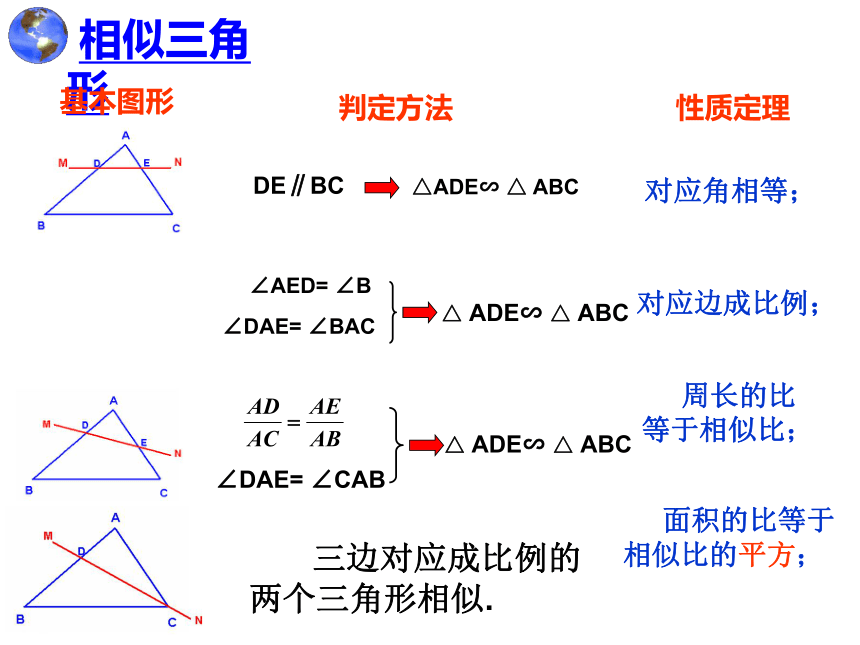
相似三角形
DE∥BC
△ ADE∽ △ ABC
∠DAE= ∠CAB
△ ADE∽ △ ABC
基本图形
判定方法
∠AED= ∠B
∠DAE= ∠BAC
△ADE∽ △ ABC
对应角相等;
性质定理
对应边成比例;
周长的比
等于相似比;
面积的比等于
相似比的平方;
三边对应成比例的
两个三角形相似.
练一练
基本图形
D
E
M
N
H
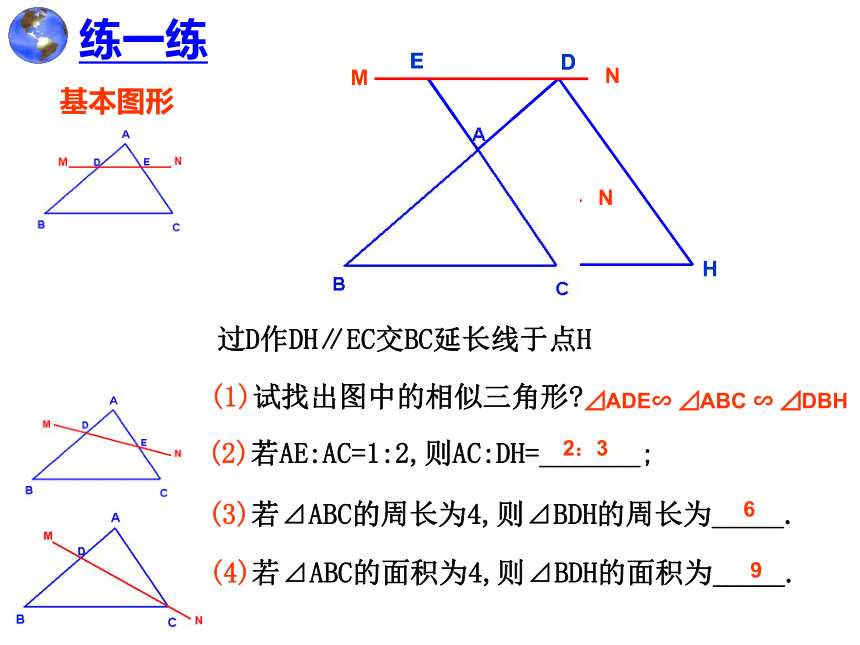
过D作DH∥EC交BC延长线于点H
(1)试找出图中的相似三角形
(2)若AE:AC=1:2,则AC:DH=_______;
(3)若⊿ABC的周长为4,则⊿BDH的周长为_____.
(4)若⊿ABC的面积为4,则⊿BDH的面积为_____.
⊿ADE∽ ⊿ABC ∽ ⊿DBH
2:3
6
9
D
E
M
N
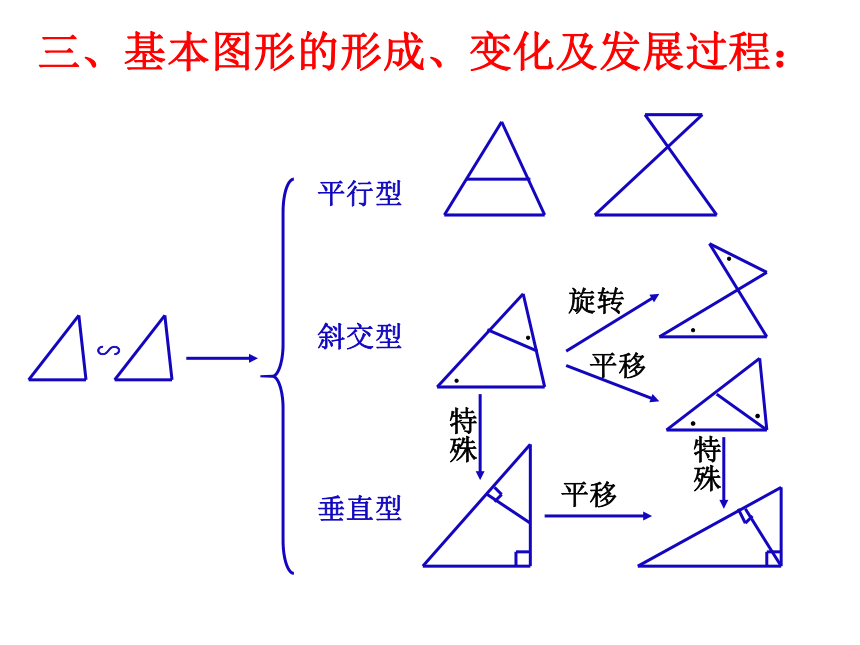
三、基本图形的形成、变化及发展过程:
∽
平行型
斜交型
.
.
.
.
.
.
旋转
平移
垂直型
特殊
特殊
平移
学以致用
E
F
B
G
D
C
A
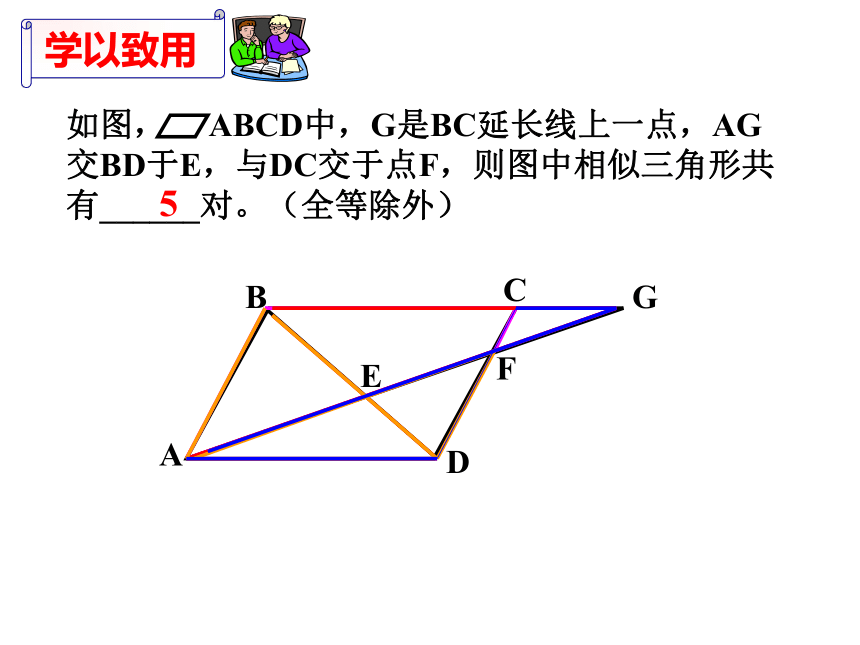
如图, ABCD中,G是BC延长线上一点,AG交BD于E,与DC交于点F,则图中相似三角形共有______对。(全等除外)
5
学以致用
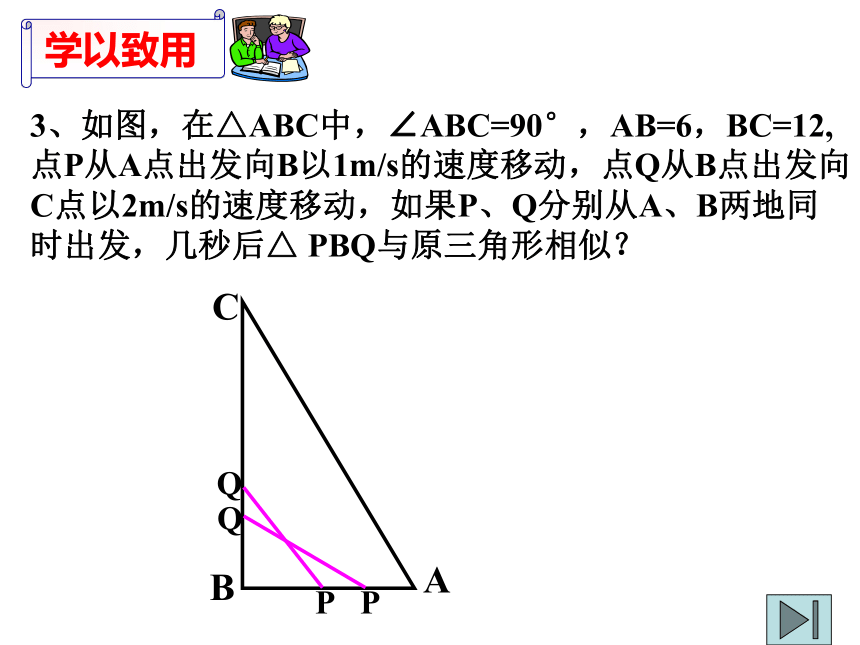
3、如图,在△ABC中,∠ABC=90°,AB=6,BC=12,点P从A点出发向B以1m/s的速度移动,点Q从B点出发向C点以2m/s的速度移动,如果P、Q分别从A、B两地同时出发,几秒后△ PBQ与原三角形相似?
A
B
C
Q
P
Q
P
A
B
C
E
F
如图,在正方形ABCD中,E为BC上任意一点(与B、C不重合)∠AEF=90°.观察图形:
D
A
B
C
E
F
D
(2)若E为BC的中点,连结AF,图中有哪些相似三角形?
(1) △ABE 与△ECF 是否相似?并证明你的结论。
△ABE∽ △ECF
∽ △AEF
问题1:
(1)点E为BC上任意一点,若 ∠B= ∠C=60°, ∠AEF= ∠ C,则△ABE与△ ECF的关系还成立吗?说明理由
(2)点E为BC上任意一点若 ∠B= ∠C= α, ∠AEF= ∠ C,则△ABE 与△ ECF的关系还成立吗?
C
60°
60°
60°
A
B
E
F
α
α
α
A
B
C
E
F
α
α
α
A
B
F
C
E
60°
60°
60°
C
A
B
E
F
△ABE∽ △ECF
A
B
C
E
F
α
α
α
D
A
F
α
B
C
E
α
α
D
G
(1)延长BA、CF相交于点D,且E为BC的中点,若 ∠B=∠C= α, ∠AEF= ∠ C,连结AF.
①找出图中的相似三角形
②说出图中相等的角及边之间的关系
(2)延长BA、CF相交于点D,且E为BC的中点,若 ∠B=∠C= α, ∠AEF= ∠ C, 当∠AEF旋转到如图位置时,上述关系还成立吗?
问题2:
善于运用类比、迁移的数学方法解决问题
C
A
B
E
F
A
B
C
E
F
A
B
C
E
F
α
α
α
A
B
C
E
F
α
α
α
D
①
②
③
①
②
①
②
③
①
②
E为中点
E
B
C
D
F
已知:D为BC上一点, ∠B= ∠C= ∠EDF=60°,BE=6,CD=3,CF=4,
则AF=_______
7
A
C
A
B
E
D
C
A
B
E
D
C
A
B
E
D
A
B
C
E
D
α
α
α
A
B
C
E
D
F
α
α
α
α
α
α
O
A
B
C
D
P
1、已知:等边△ABC 中,P为直线AC上一动点,连结BP,作∠BPQ=60°,交直线BC于点N.
(1)当P在线段AC上时,证明PA·PC=AB ·CN
(2)若P在AC的延长线上,上述关系是否成立?
(3)若P在CA的延长线上, CN=1.5,BC=2,求AP、BP的长
N
B
C
A
Q
N
B
C
A
Q
N
B
C
A
Q
P
60°
60°
60°
P
P
通过这节课的学习活动你有哪些收获?
你还有什么想法吗?
提出一个问题往往比解决一个问题更重要。----------爱因斯坦
不经历风雨怎能见彩虹,没有谁能随随便便成功!加油!!
再见
△ABC∽△A/B/C/,如果BC=3,B/C/=1.5,那么△A/B/C/
与 △ABC的相似比为_________.
1.相似三角形的定义:
对应角相等、对应边成比例的三角形叫做相似三角形。
2.相似比:
相似三角形的对应边的比,叫做相似三角形的相似比。
相似三角形
DE∥BC
△ ADE∽ △ ABC
∠DAE= ∠CAB
△ ADE∽ △ ABC
基本图形
判定方法
∠AED= ∠B
∠DAE= ∠BAC
△ADE∽ △ ABC
对应角相等;
性质定理
对应边成比例;
周长的比
等于相似比;
面积的比等于
相似比的平方;
三边对应成比例的
两个三角形相似.
练一练
基本图形
D
E
M
N
H
过D作DH∥EC交BC延长线于点H
(1)试找出图中的相似三角形
(2)若AE:AC=1:2,则AC:DH=_______;
(3)若⊿ABC的周长为4,则⊿BDH的周长为_____.
(4)若⊿ABC的面积为4,则⊿BDH的面积为_____.
⊿ADE∽ ⊿ABC ∽ ⊿DBH
2:3
6
9
D
E
M
N
三、基本图形的形成、变化及发展过程:
∽
平行型
斜交型
.
.
.
.
.
.
旋转
平移
垂直型
特殊
特殊
平移
学以致用
E
F
B
G
D
C
A
如图, ABCD中,G是BC延长线上一点,AG交BD于E,与DC交于点F,则图中相似三角形共有______对。(全等除外)
5
学以致用
3、如图,在△ABC中,∠ABC=90°,AB=6,BC=12,点P从A点出发向B以1m/s的速度移动,点Q从B点出发向C点以2m/s的速度移动,如果P、Q分别从A、B两地同时出发,几秒后△ PBQ与原三角形相似?
A
B
C
Q
P
Q
P
A
B
C
E
F
如图,在正方形ABCD中,E为BC上任意一点(与B、C不重合)∠AEF=90°.观察图形:
D
A
B
C
E
F
D
(2)若E为BC的中点,连结AF,图中有哪些相似三角形?
(1) △ABE 与△ECF 是否相似?并证明你的结论。
△ABE∽ △ECF
∽ △AEF
问题1:
(1)点E为BC上任意一点,若 ∠B= ∠C=60°, ∠AEF= ∠ C,则△ABE与△ ECF的关系还成立吗?说明理由
(2)点E为BC上任意一点若 ∠B= ∠C= α, ∠AEF= ∠ C,则△ABE 与△ ECF的关系还成立吗?
C
60°
60°
60°
A
B
E
F
α
α
α
A
B
C
E
F
α
α
α
A
B
F
C
E
60°
60°
60°
C
A
B
E
F
△ABE∽ △ECF
A
B
C
E
F
α
α
α
D
A
F
α
B
C
E
α
α
D
G
(1)延长BA、CF相交于点D,且E为BC的中点,若 ∠B=∠C= α, ∠AEF= ∠ C,连结AF.
①找出图中的相似三角形
②说出图中相等的角及边之间的关系
(2)延长BA、CF相交于点D,且E为BC的中点,若 ∠B=∠C= α, ∠AEF= ∠ C, 当∠AEF旋转到如图位置时,上述关系还成立吗?
问题2:
善于运用类比、迁移的数学方法解决问题
C
A
B
E
F
A
B
C
E
F
A
B
C
E
F
α
α
α
A
B
C
E
F
α
α
α
D
①
②
③
①
②
①
②
③
①
②
E为中点
E
B
C
D
F
已知:D为BC上一点, ∠B= ∠C= ∠EDF=60°,BE=6,CD=3,CF=4,
则AF=_______
7
A
C
A
B
E
D
C
A
B
E
D
C
A
B
E
D
A
B
C
E
D
α
α
α
A
B
C
E
D
F
α
α
α
α
α
α
O
A
B
C
D
P
1、已知:等边△ABC 中,P为直线AC上一动点,连结BP,作∠BPQ=60°,交直线BC于点N.
(1)当P在线段AC上时,证明PA·PC=AB ·CN
(2)若P在AC的延长线上,上述关系是否成立?
(3)若P在CA的延长线上, CN=1.5,BC=2,求AP、BP的长
N
B
C
A
Q
N
B
C
A
Q
N
B
C
A
Q
P
60°
60°
60°
P
P
通过这节课的学习活动你有哪些收获?
你还有什么想法吗?
提出一个问题往往比解决一个问题更重要。----------爱因斯坦
不经历风雨怎能见彩虹,没有谁能随随便便成功!加油!!
再见
