第五章 投影与视图 复习课件(共30张PPT)
文档属性
| 名称 | 第五章 投影与视图 复习课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
《第五章投影与视图》
你猜我猜小游戏
下面的图片表示什么?
用一句话说出你的感悟:。。。
学习目标:
1.学习用思维导图的方式进行本章知识点的梳理与归纳;
2.运用配置有关例题及习题更加深入全面地思考巩固全章知识.
学习重点、难点:
会制作知识结构图,并运用相关知识解决实际问题.
第一环节
归纳梳理 展示交流
第二环节
评价与引领 建议与欣赏
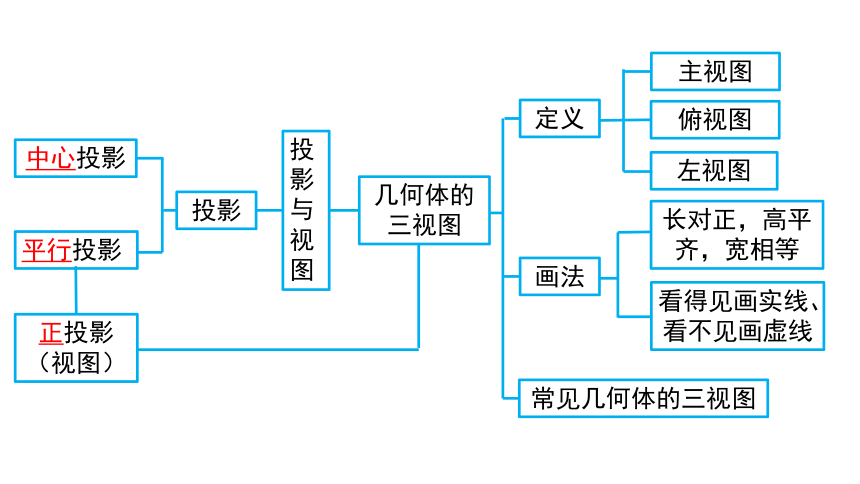
正投影
(视图)
平行投影
中心投影
投影
投影与视图
几何体的三视图
长对正,高平齐,宽相等
看得见画实线、
看不见画虚线
常见几何体的三视图
画法
定义
左视图
俯视图
主视图
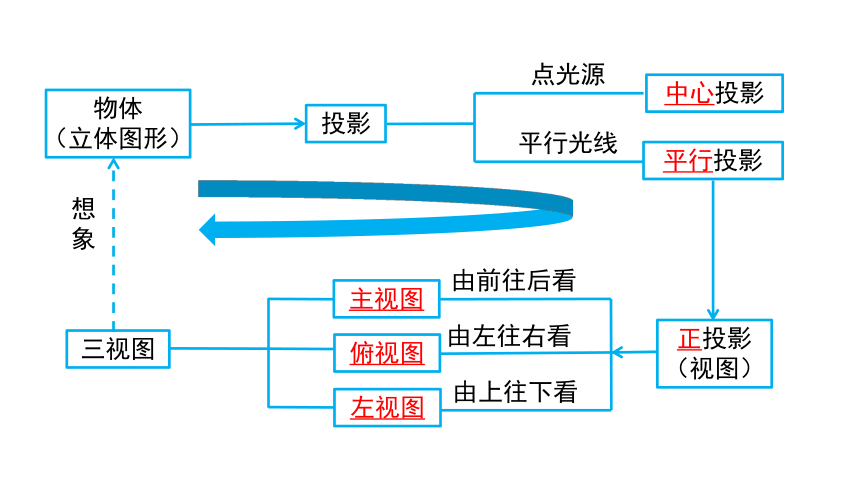
物体
(立体图形)
投影
主视图
俯视图
左视图
正投影
(视图)
平行投影
中心投影
三视图
由上往下看
平行光线
点光源
由左往右看
由前往后看
想象
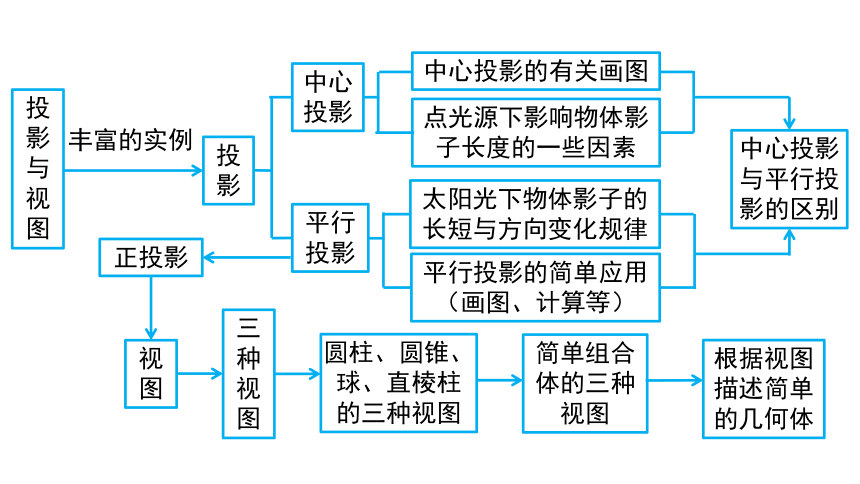
简单组合体的三种视图
投影与视图
圆柱、圆锥、球、直棱柱的三种视图
三种视图
平行投影的简单应用
(画图、计算等)
视图
正投影
点光源下影响物体影子长度的一些因素
太阳光下物体影子的长短与方向变化规律
中心投影的有关画图
中心投影与平行投影的区别
平行投影
中心投影
根据视图描述简单的几何体
丰富的实例
投影
第三环节
典型例题
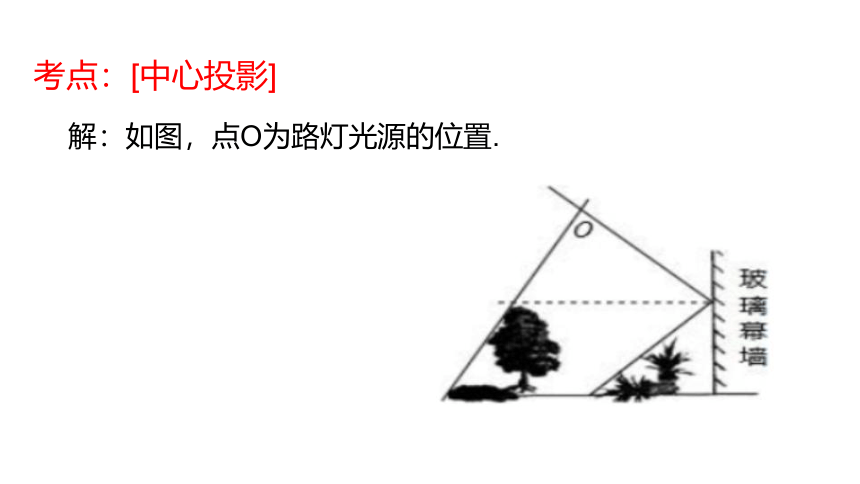
例1. 与一盏路灯相对,有一玻璃幕墙幕墙,前面的地面上有一盆花和一棵树. 晚上,幕墙反射路灯灯光形成了那盆花的影子(如图所示),树影是路灯灯光形成的. 请你确定此时路灯光源的位置.
考点:[中心投影]
考点:[中心投影]
解:如图,点O为路灯光源的位置.
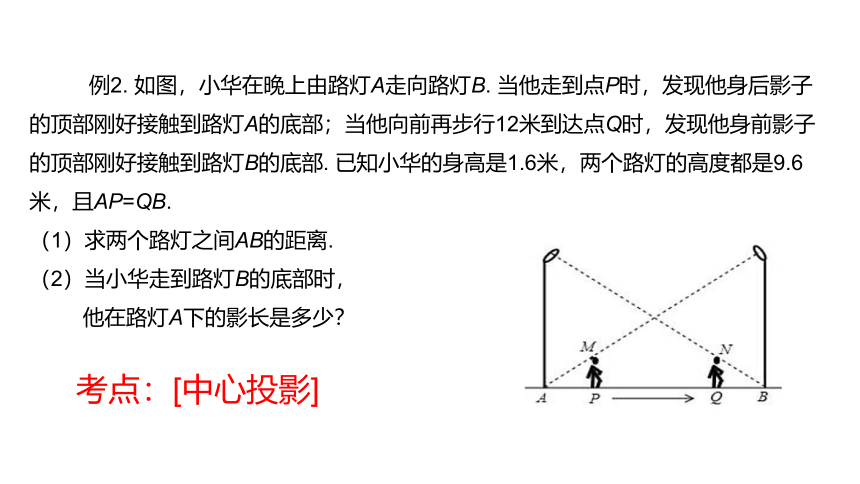
例2. 如图,小华在晚上由路灯A走向路灯B. 当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12米到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部. 已知小华的身高是1.6米,两个路灯的高度都是9.6米,且AP=QB.
(1)求两个路灯之间AB的距离.
(2)当小华走到路灯B的底部时,
他在路灯A下的影长是多少?
考点:[中心投影]
例3. 如图,小明与同学合作利用太阳光线测量旗杆的高度,身高1.6 m的小明落在地面上的影长为BC=2.4 m.
(1)请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG;
(2)若小明测得此刻旗杆落在地面的影长EG=16 m,请求出旗杆DE的高度.
考点:[平行投影]
考点:[中心投影]
例4. 我国古代数学家利用 “牟合方盖” 找到了球体体积的计算方法. “牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图所示的几何体是可以形成 “牟合方盖” 的一种模型,它的主视图是( ).
C
例5. 如图是一个几何体的三视图,根据图示的数据可计算出该几何体的表面积为 .
90π
第四环节
实战训练 巩固提升
1.将两个长方体如图放置,则所构成的几何体的左视图可能
是( ).
C
2.如图所示,该几何体的左视图是( ).
B
3.鲁班锁,民间也称作孔明锁、八卦锁,它起源于中国古代建筑中首创的榫卯结构,如图是鲁班锁的其中一个部件,它的主视图是( ).
C
4.观察如图所示的三种视图,与之对应的物体是( ).
D
第五环节
课堂检测 收获成果
1.如图是由10个同样大小的小正方体摆成的几何体. 将小正方体①移走后,则关于新几何体的三视图描述正确的是( ).
A.俯视图不变,左视图不变
B.主视图改变,左视图改变
C.俯视图不变,主视图不变
D.主视图改变,俯视图改变
A
2.小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的投影不可能的是( ).
A
3.(2018年山东省临沂市)如图是一个几何体的三视图(图中尺寸单位:cm). 根据图中所示数据求得这个几何体的侧面积是( ).
C
4.两个大小不同的球在水平面上靠在一起,组成如图所示的几何体,则该几何体的左视图是( ).
C
5. “皮影戏” 作为我国一种民间艺术,对它的叙述错误的是( ).
A.它是用兽皮或纸板做成的人物剪影,来表演故事的戏曲
B.表演时,要用灯光把剪影照在银幕上
C.灯光下,做不同的手势可以形成不同的手影
D.表演时,也可用阳光把剪影照在银幕上
D
第六环节
课堂小结
谢谢倾听!
《第五章投影与视图》
你猜我猜小游戏
下面的图片表示什么?
用一句话说出你的感悟:。。。
学习目标:
1.学习用思维导图的方式进行本章知识点的梳理与归纳;
2.运用配置有关例题及习题更加深入全面地思考巩固全章知识.
学习重点、难点:
会制作知识结构图,并运用相关知识解决实际问题.
第一环节
归纳梳理 展示交流
第二环节
评价与引领 建议与欣赏
正投影
(视图)
平行投影
中心投影
投影
投影与视图
几何体的三视图
长对正,高平齐,宽相等
看得见画实线、
看不见画虚线
常见几何体的三视图
画法
定义
左视图
俯视图
主视图
物体
(立体图形)
投影
主视图
俯视图
左视图
正投影
(视图)
平行投影
中心投影
三视图
由上往下看
平行光线
点光源
由左往右看
由前往后看
想象
简单组合体的三种视图
投影与视图
圆柱、圆锥、球、直棱柱的三种视图
三种视图
平行投影的简单应用
(画图、计算等)
视图
正投影
点光源下影响物体影子长度的一些因素
太阳光下物体影子的长短与方向变化规律
中心投影的有关画图
中心投影与平行投影的区别
平行投影
中心投影
根据视图描述简单的几何体
丰富的实例
投影
第三环节
典型例题
例1. 与一盏路灯相对,有一玻璃幕墙幕墙,前面的地面上有一盆花和一棵树. 晚上,幕墙反射路灯灯光形成了那盆花的影子(如图所示),树影是路灯灯光形成的. 请你确定此时路灯光源的位置.
考点:[中心投影]
考点:[中心投影]
解:如图,点O为路灯光源的位置.
例2. 如图,小华在晚上由路灯A走向路灯B. 当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12米到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部. 已知小华的身高是1.6米,两个路灯的高度都是9.6米,且AP=QB.
(1)求两个路灯之间AB的距离.
(2)当小华走到路灯B的底部时,
他在路灯A下的影长是多少?
考点:[中心投影]
例3. 如图,小明与同学合作利用太阳光线测量旗杆的高度,身高1.6 m的小明落在地面上的影长为BC=2.4 m.
(1)请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG;
(2)若小明测得此刻旗杆落在地面的影长EG=16 m,请求出旗杆DE的高度.
考点:[平行投影]
考点:[中心投影]
例4. 我国古代数学家利用 “牟合方盖” 找到了球体体积的计算方法. “牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图所示的几何体是可以形成 “牟合方盖” 的一种模型,它的主视图是( ).
C
例5. 如图是一个几何体的三视图,根据图示的数据可计算出该几何体的表面积为 .
90π
第四环节
实战训练 巩固提升
1.将两个长方体如图放置,则所构成的几何体的左视图可能
是( ).
C
2.如图所示,该几何体的左视图是( ).
B
3.鲁班锁,民间也称作孔明锁、八卦锁,它起源于中国古代建筑中首创的榫卯结构,如图是鲁班锁的其中一个部件,它的主视图是( ).
C
4.观察如图所示的三种视图,与之对应的物体是( ).
D
第五环节
课堂检测 收获成果
1.如图是由10个同样大小的小正方体摆成的几何体. 将小正方体①移走后,则关于新几何体的三视图描述正确的是( ).
A.俯视图不变,左视图不变
B.主视图改变,左视图改变
C.俯视图不变,主视图不变
D.主视图改变,俯视图改变
A
2.小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的投影不可能的是( ).
A
3.(2018年山东省临沂市)如图是一个几何体的三视图(图中尺寸单位:cm). 根据图中所示数据求得这个几何体的侧面积是( ).
C
4.两个大小不同的球在水平面上靠在一起,组成如图所示的几何体,则该几何体的左视图是( ).
C
5. “皮影戏” 作为我国一种民间艺术,对它的叙述错误的是( ).
A.它是用兽皮或纸板做成的人物剪影,来表演故事的戏曲
B.表演时,要用灯光把剪影照在银幕上
C.灯光下,做不同的手势可以形成不同的手影
D.表演时,也可用阳光把剪影照在银幕上
D
第六环节
课堂小结
谢谢倾听!
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
