第一章 特殊平行四边形 复习课件(共31张PPT)
文档属性
| 名称 | 第一章 特殊平行四边形 复习课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 21:22:08 | ||
图片预览




文档简介
(共31张PPT)
第一章 特殊平行四边形
本章总结提升
第一章 特殊平行四边形
知识结构关系
重点模块总结
综合能力提升
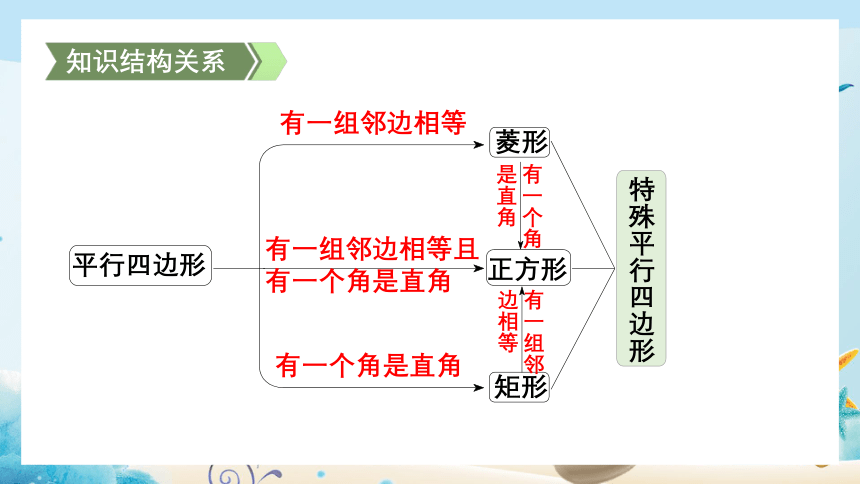
平行四边形
有一组邻边相等
有一组邻边相等且有一个角是直角
有一个角是直角
菱形
正方形
矩形
有一个角是直角
有一组邻边相等
特殊平行四边形
知识结构关系
模块1 菱形的性质与判定
菱形的性质与判定有哪些?它与平行四边形有何关系?你能用几种方法计算菱形的面积?
重点模块总结
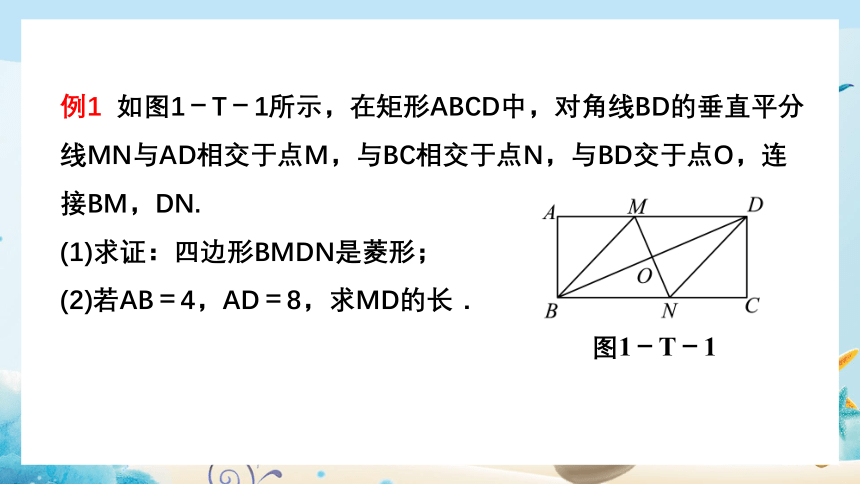
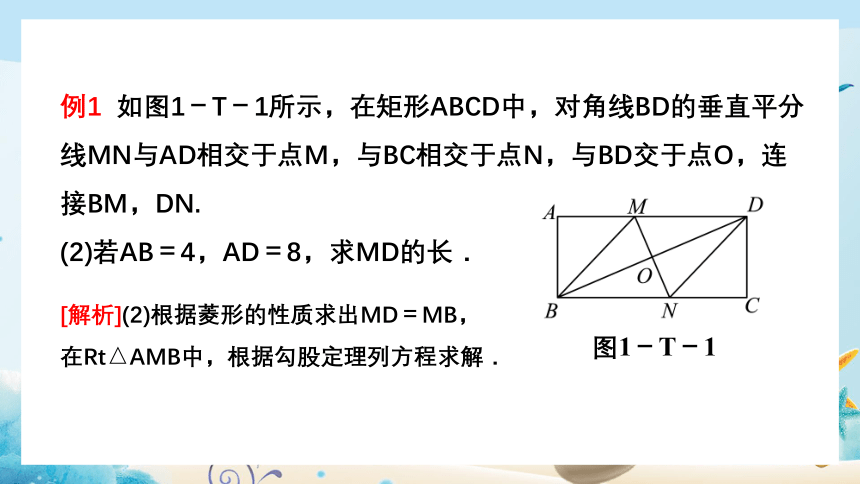
例1 如图1-T-1所示,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,与BD交于点O,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
图1-T-1
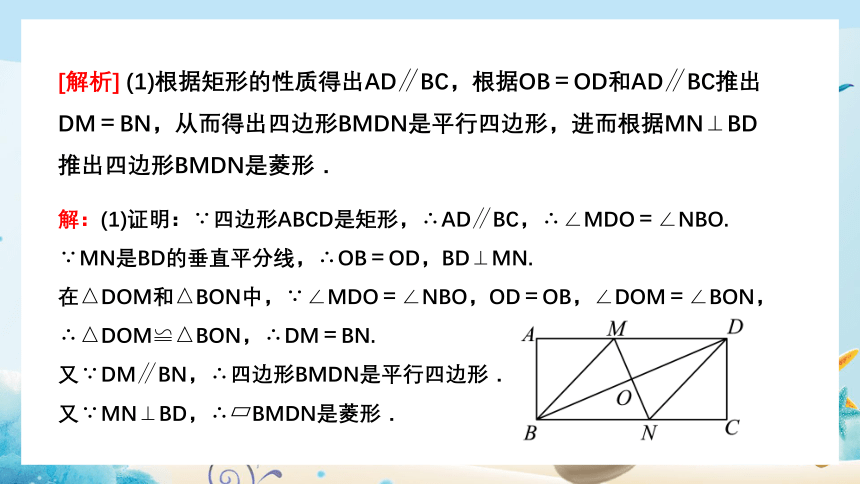
[解析] (1)根据矩形的性质得出AD∥BC,根据OB=OD和AD∥BC推出DM=BN,从而得出四边形BMDN是平行四边形,进而根据MN⊥BD推出四边形BMDN是菱形.
解:(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠MDO=∠NBO.
∵MN是BD的垂直平分线,∴OB=OD,BD⊥MN.
在△DOM和△BON中,∵∠MDO=∠NBO,OD=OB,∠DOM=∠BON,
∴△DOM≌△BON,∴DM=BN.
又∵DM∥BN,∴四边形BMDN是平行四边形.
又∵MN⊥BD,∴ BMDN是菱形.
例1 如图1-T-1所示,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,与BD交于点O,连接BM,DN.
(2)若AB=4,AD=8,求MD的长.
图1-T-1
[解析](2)根据菱形的性质求出MD=MB,
在Rt△AMB中,根据勾股定理列方程求解.
解:(2)∵四边形BMDN是菱形,∴MB=MD.
设MD=x,则MB=MD=x,AM=8-x.
在Rt△AMB中,MB2=AM2+AB2,
即x2=(8-x)2+42,解得x=5,
即MD的长为5.
模块2 矩形的性质与判定
矩形的性质与判定有哪些?它与平行四边形有何关系?矩形与菱形有何异同点?利用矩形对角线的性质可得到直角三角形的哪个性质?
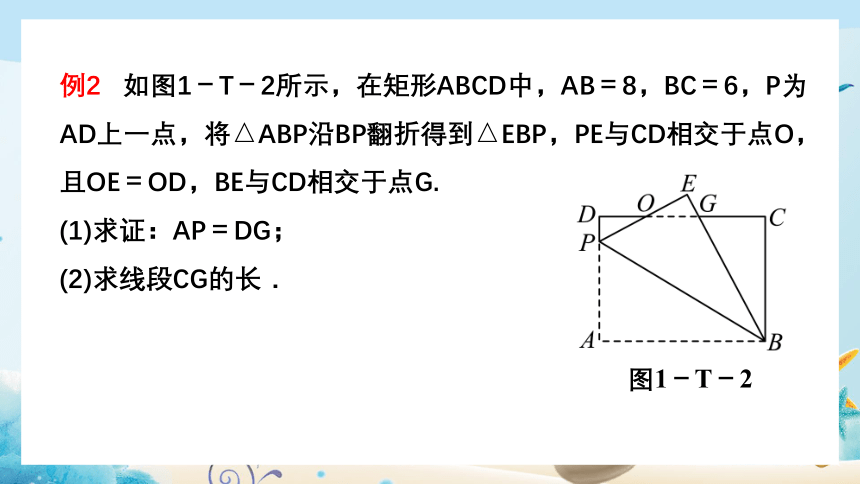
例2 如图1-T-2所示,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折得到△EBP,PE与CD相交于点O,且OE=OD,BE与CD相交于点G.
(1)求证:AP=DG;
(2)求线段CG的长.
图1-T-2
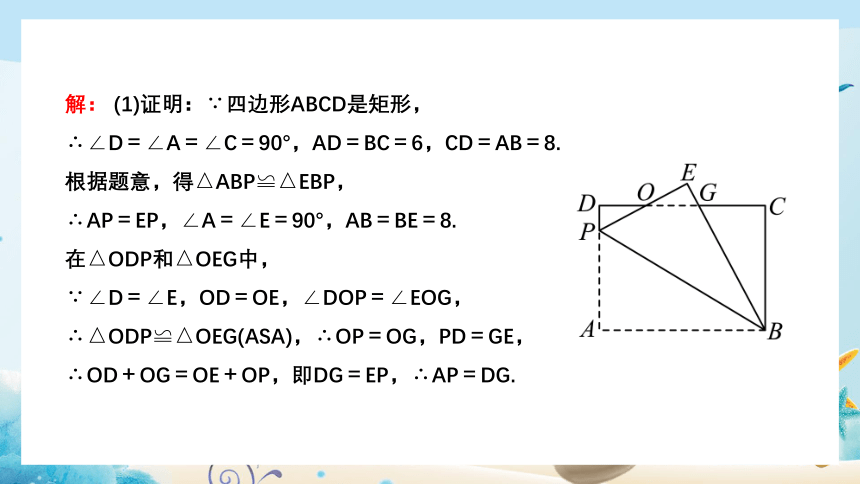
解: (1)证明:∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8.
根据题意,得△ABP≌△EBP,
∴AP=EP,∠A=∠E=90°,AB=BE=8.
在△ODP和△OEG中,
∵∠D=∠E,OD=OE,∠DOP=∠EOG,
∴△ODP≌△OEG(ASA),∴OP=OG,PD=GE,
∴OD+OG=OE+OP,即DG=EP,∴AP=DG.
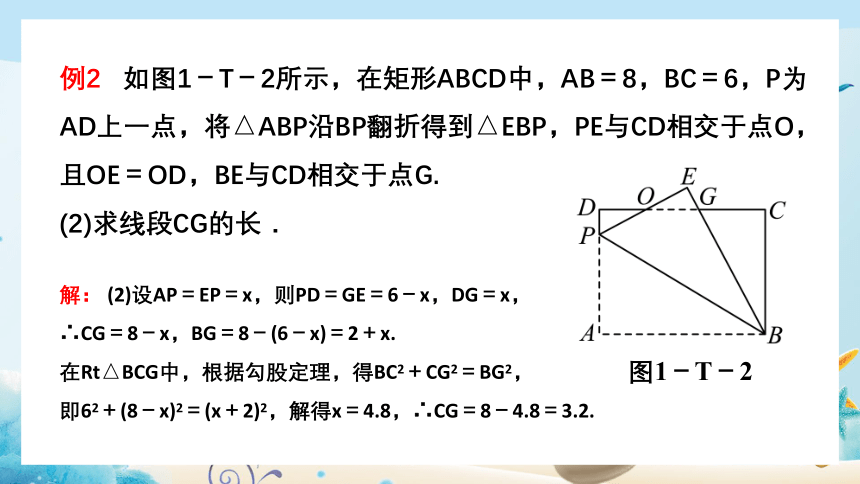
例2 如图1-T-2所示,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折得到△EBP,PE与CD相交于点O,且OE=OD,BE与CD相交于点G.
(2)求线段CG的长.
图1-T-2
解: (2)设AP=EP=x,则PD=GE=6-x,DG=x,
∴CG=8-x,BG=8-(6-x)=2+x.
在Rt△BCG中,根据勾股定理,得BC2+CG2=BG2,
即62+(8-x)2=(x+2)2,解得x=4.8,∴CG=8-4.8=3.2.
【归纳总结】解决矩形中折叠问题的关键点:
(1)抓住折叠的本质:①折起部分与重合部分是全等的;②利用轴对称的性质(对称轴垂直平分对应点所连线段).
(2)找出隐含的折叠前后的位置关系和数量关系.
(3)结合三角形全等、勾股定理等知识,设出恰当的未知数,列出方程求解.
例3 如图1-T-3,在 ABCD中,各内角的平分线相交于点E,F,G,H.
(1)求证:四边形EFGH是矩形;
(2)若AB=6,BC=4,∠BAD=60°,
求四边形EFGH的面积.
图1-T-3
例3 如图1-T-3,在 ABCD中,各内角的平分线相交于点E,F,G,H.
(2)若AB=6,BC=4,∠BAD=60°,
求四边形EFGH的面积.
图1-T-3
例4 如图1-T-4,在四边形ABCD中,∠DAB=90°,DB=DC,E,F分别为DB,BC的中点,连接AE,EF,AF.
(1)求证:AE=EF;
(2)当AF=AE时,设∠ADB=α,
∠CDB=β,求α,β之间的数量关系.
图1-T-3
例4 如图1-T-4,在四边形ABCD中,∠DAB=90°,DB=DC,E,F分别为DB,BC的中点,连接AE,EF,AF.
(2)当AF=AE时,设∠ADB=α,
∠CDB=β,求α,β之间的数量关系.
图1-T-3
解:(2)∵AE是Rt△ABD的斜边BD上的中线,
∴AE=DE,∴∠ADB=∠DAE,∴∠AEB=2∠ADB=2α.
∵EF是△BCD的中位线,∴EF∥DC,∴∠FEB=∠CDB=β.
由(1)知AE=EF,又AF=AE,
∴AE=EF=AF,∴△AEF是等边三角形,
∴∠AEF=60°,
即∠AEF=∠AEB+∠FEB=2α+β=60°,
∴2α+β=60°.
模块3 正方形的性质与判定
正方形的性质与判定有哪些?四边形、平行四边形、菱形、矩形、正方形之间有怎样的关系?
例5 如图1-T-5,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,
CD,AD上,AH=2,连接CF.
(1)若DG=2,求证:四边形EFGH为正方形;
(2)若DG=6,求△FCG的面积.
图1-T-3
[解析] (1)通过证明Rt△DHG≌Rt△AEH,得到∠DHG=∠AEH,从而得到∠GHE=90°,然后根据有一个角为直角的菱形为正方形得到四边形EFGH为正方形;
解:(1)证明:∵四边形EFGH为菱形,∴HG=EH.
∵AH=2,DG=2,∴DG=AH.
在Rt△DHG和Rt△AEH中,∵HG=EH,DG=AH,
∴Rt△DHG≌Rt△AEH,∴∠DHG=∠AEH.
∵∠AEH+∠AHE=90°,∴∠DHG+∠AHE=90°,∴∠GHE=90°.
又∵四边形EFGH为菱形,∴四边形EFGH为正方形.
例5 如图1-T-5,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,
CD,AD上,AH=2,连接CF.
(2)若DG=6,求△FCG的面积.
图1-T-3
[解析](2)过点F作FQ⊥CD于点Q,连接GE,利用
AB∥CD得到∠AEG=∠QGE,再根据菱形的性质得HE=FG,HE∥FG,则∠HEG=∠FGE,所以∠AEH=∠QGF,于是可证明△AEH≌△QGF,得到AH=QF=2,然后根据三角形面积公式求解.
【归纳总结】正方形既是矩形,又是菱形,它具有矩形和菱形的所有性质,判定一个四边形是正方形只需要保证它既是矩形又是菱形即可.
例6 如图1-T-6①所示,在正方形ABCD和正方形CGEF中,点B,C,F在同一条直线上,M是线段AE的中点,连接DM,FM.
(1)求证:DM⊥FM,DM=FM;
(2)如图1-T-6②,若将“正方形
ABCD和正方形CGEF”改为“菱形
ABCD和菱形CGEF”,且∠BCD=
∠G=120°,其他条件不变,则DM和FM又有怎样的位置关系和数量关系?直接写出结论.
图1-T-6
综合能力提升
解:(1)证明:如图,延长DM交GE于点N,连接DF,NF.
∵四边形ABCD和四边形CGEF都是正方形,∴AD∥BC,BC∥GE,
∴AD∥GE,∴∠DAM=∠NEM.∵M是AE的中点,∴AM=EM.
又∵∠AMD=∠EMN,∴△MAD≌△MEN,
∴DM=NM,AD=EN.∵AD=CD,∴CD=EN.
又∵CF=EF,∠FCD=∠FEN=90°,
∴△DCF≌△NEF,∴∠CFD=∠EFN,DF=NF.
∵DM=NM,∴FM平分∠DFN,且DM⊥FM.
∵∠EFN+∠CFN=90°,∴∠CFD+∠CFN=90°,即∠DFN=90°.
∵DM=NM,∴FM是Rt△DFN斜边上的中线,∴DM=FM.
例6 如图1-T-6①所示,在正方形ABCD和正方形CGEF中,点B,C,F在同一条直线上,M是线段AE的中点,连接DM,FM.
(2)如图1-T-6②,若将“正方形
ABCD和正方形CGEF”改为“菱形
ABCD和菱形CGEF”,且∠BCD=
∠G=120°,其他条件不变,则DM和FM
又有怎样的位置关系和数量关系?直接写出结论.
图1-T-6
谢 谢
第一章 特殊平行四边形
本章总结提升
第一章 特殊平行四边形
知识结构关系
重点模块总结
综合能力提升
平行四边形
有一组邻边相等
有一组邻边相等且有一个角是直角
有一个角是直角
菱形
正方形
矩形
有一个角是直角
有一组邻边相等
特殊平行四边形
知识结构关系
模块1 菱形的性质与判定
菱形的性质与判定有哪些?它与平行四边形有何关系?你能用几种方法计算菱形的面积?
重点模块总结
例1 如图1-T-1所示,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,与BD交于点O,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
图1-T-1
[解析] (1)根据矩形的性质得出AD∥BC,根据OB=OD和AD∥BC推出DM=BN,从而得出四边形BMDN是平行四边形,进而根据MN⊥BD推出四边形BMDN是菱形.
解:(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠MDO=∠NBO.
∵MN是BD的垂直平分线,∴OB=OD,BD⊥MN.
在△DOM和△BON中,∵∠MDO=∠NBO,OD=OB,∠DOM=∠BON,
∴△DOM≌△BON,∴DM=BN.
又∵DM∥BN,∴四边形BMDN是平行四边形.
又∵MN⊥BD,∴ BMDN是菱形.
例1 如图1-T-1所示,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,与BD交于点O,连接BM,DN.
(2)若AB=4,AD=8,求MD的长.
图1-T-1
[解析](2)根据菱形的性质求出MD=MB,
在Rt△AMB中,根据勾股定理列方程求解.
解:(2)∵四边形BMDN是菱形,∴MB=MD.
设MD=x,则MB=MD=x,AM=8-x.
在Rt△AMB中,MB2=AM2+AB2,
即x2=(8-x)2+42,解得x=5,
即MD的长为5.
模块2 矩形的性质与判定
矩形的性质与判定有哪些?它与平行四边形有何关系?矩形与菱形有何异同点?利用矩形对角线的性质可得到直角三角形的哪个性质?
例2 如图1-T-2所示,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折得到△EBP,PE与CD相交于点O,且OE=OD,BE与CD相交于点G.
(1)求证:AP=DG;
(2)求线段CG的长.
图1-T-2
解: (1)证明:∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8.
根据题意,得△ABP≌△EBP,
∴AP=EP,∠A=∠E=90°,AB=BE=8.
在△ODP和△OEG中,
∵∠D=∠E,OD=OE,∠DOP=∠EOG,
∴△ODP≌△OEG(ASA),∴OP=OG,PD=GE,
∴OD+OG=OE+OP,即DG=EP,∴AP=DG.
例2 如图1-T-2所示,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折得到△EBP,PE与CD相交于点O,且OE=OD,BE与CD相交于点G.
(2)求线段CG的长.
图1-T-2
解: (2)设AP=EP=x,则PD=GE=6-x,DG=x,
∴CG=8-x,BG=8-(6-x)=2+x.
在Rt△BCG中,根据勾股定理,得BC2+CG2=BG2,
即62+(8-x)2=(x+2)2,解得x=4.8,∴CG=8-4.8=3.2.
【归纳总结】解决矩形中折叠问题的关键点:
(1)抓住折叠的本质:①折起部分与重合部分是全等的;②利用轴对称的性质(对称轴垂直平分对应点所连线段).
(2)找出隐含的折叠前后的位置关系和数量关系.
(3)结合三角形全等、勾股定理等知识,设出恰当的未知数,列出方程求解.
例3 如图1-T-3,在 ABCD中,各内角的平分线相交于点E,F,G,H.
(1)求证:四边形EFGH是矩形;
(2)若AB=6,BC=4,∠BAD=60°,
求四边形EFGH的面积.
图1-T-3
例3 如图1-T-3,在 ABCD中,各内角的平分线相交于点E,F,G,H.
(2)若AB=6,BC=4,∠BAD=60°,
求四边形EFGH的面积.
图1-T-3
例4 如图1-T-4,在四边形ABCD中,∠DAB=90°,DB=DC,E,F分别为DB,BC的中点,连接AE,EF,AF.
(1)求证:AE=EF;
(2)当AF=AE时,设∠ADB=α,
∠CDB=β,求α,β之间的数量关系.
图1-T-3
例4 如图1-T-4,在四边形ABCD中,∠DAB=90°,DB=DC,E,F分别为DB,BC的中点,连接AE,EF,AF.
(2)当AF=AE时,设∠ADB=α,
∠CDB=β,求α,β之间的数量关系.
图1-T-3
解:(2)∵AE是Rt△ABD的斜边BD上的中线,
∴AE=DE,∴∠ADB=∠DAE,∴∠AEB=2∠ADB=2α.
∵EF是△BCD的中位线,∴EF∥DC,∴∠FEB=∠CDB=β.
由(1)知AE=EF,又AF=AE,
∴AE=EF=AF,∴△AEF是等边三角形,
∴∠AEF=60°,
即∠AEF=∠AEB+∠FEB=2α+β=60°,
∴2α+β=60°.
模块3 正方形的性质与判定
正方形的性质与判定有哪些?四边形、平行四边形、菱形、矩形、正方形之间有怎样的关系?
例5 如图1-T-5,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,
CD,AD上,AH=2,连接CF.
(1)若DG=2,求证:四边形EFGH为正方形;
(2)若DG=6,求△FCG的面积.
图1-T-3
[解析] (1)通过证明Rt△DHG≌Rt△AEH,得到∠DHG=∠AEH,从而得到∠GHE=90°,然后根据有一个角为直角的菱形为正方形得到四边形EFGH为正方形;
解:(1)证明:∵四边形EFGH为菱形,∴HG=EH.
∵AH=2,DG=2,∴DG=AH.
在Rt△DHG和Rt△AEH中,∵HG=EH,DG=AH,
∴Rt△DHG≌Rt△AEH,∴∠DHG=∠AEH.
∵∠AEH+∠AHE=90°,∴∠DHG+∠AHE=90°,∴∠GHE=90°.
又∵四边形EFGH为菱形,∴四边形EFGH为正方形.
例5 如图1-T-5,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,
CD,AD上,AH=2,连接CF.
(2)若DG=6,求△FCG的面积.
图1-T-3
[解析](2)过点F作FQ⊥CD于点Q,连接GE,利用
AB∥CD得到∠AEG=∠QGE,再根据菱形的性质得HE=FG,HE∥FG,则∠HEG=∠FGE,所以∠AEH=∠QGF,于是可证明△AEH≌△QGF,得到AH=QF=2,然后根据三角形面积公式求解.
【归纳总结】正方形既是矩形,又是菱形,它具有矩形和菱形的所有性质,判定一个四边形是正方形只需要保证它既是矩形又是菱形即可.
例6 如图1-T-6①所示,在正方形ABCD和正方形CGEF中,点B,C,F在同一条直线上,M是线段AE的中点,连接DM,FM.
(1)求证:DM⊥FM,DM=FM;
(2)如图1-T-6②,若将“正方形
ABCD和正方形CGEF”改为“菱形
ABCD和菱形CGEF”,且∠BCD=
∠G=120°,其他条件不变,则DM和FM又有怎样的位置关系和数量关系?直接写出结论.
图1-T-6
综合能力提升
解:(1)证明:如图,延长DM交GE于点N,连接DF,NF.
∵四边形ABCD和四边形CGEF都是正方形,∴AD∥BC,BC∥GE,
∴AD∥GE,∴∠DAM=∠NEM.∵M是AE的中点,∴AM=EM.
又∵∠AMD=∠EMN,∴△MAD≌△MEN,
∴DM=NM,AD=EN.∵AD=CD,∴CD=EN.
又∵CF=EF,∠FCD=∠FEN=90°,
∴△DCF≌△NEF,∴∠CFD=∠EFN,DF=NF.
∵DM=NM,∴FM平分∠DFN,且DM⊥FM.
∵∠EFN+∠CFN=90°,∴∠CFD+∠CFN=90°,即∠DFN=90°.
∵DM=NM,∴FM是Rt△DFN斜边上的中线,∴DM=FM.
例6 如图1-T-6①所示,在正方形ABCD和正方形CGEF中,点B,C,F在同一条直线上,M是线段AE的中点,连接DM,FM.
(2)如图1-T-6②,若将“正方形
ABCD和正方形CGEF”改为“菱形
ABCD和菱形CGEF”,且∠BCD=
∠G=120°,其他条件不变,则DM和FM
又有怎样的位置关系和数量关系?直接写出结论.
图1-T-6
谢 谢
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
