第二章 一元二次方程 复习课件(共23张PPT)
文档属性
| 名称 | 第二章 一元二次方程 复习课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 21:27:21 | ||
图片预览







文档简介
(共23张PPT)
第二章 一元二次方程回顾与思考
学习目标
1、通过课前自主学习,建构一元二次方程知识体系.
2、通过归纳本章习题,进行典型例题的解析.
3、能用一元二次方程解决一些简单的实际问题,体会方程是刻画现实问题的有效模型.
知识回顾
考点一 一元二次方程的定义
1、若关于x的方程(m-1)x2+mx-1=0是一元二次方程,则m的取值范围是( )
A. m≠1 B. m=1 C. m>1 D. m≠0
A
考点二 一元二次方程的解及解法
2、用简便方法解下列方程(先说岀适合的解法,并说明理由)
(1)2x2-3x-7=0 (2)9-x2=2x2-6x
(3)(x+1)(2-x)=2 (4)(3x-2)2=8
针对训练
(易错题)三角形两边长分别为3和6,第三边的长是方程x2-13+36=0的根,则该三角形的周长为( )
A.13 B.15 C.18 D.13或18
A
考点三 一元二次方程根的判别式及根与系数的关系
3、已知关于x的方程(m5)x2-4x-1=0有两个实数根,则m的取值范围是( )
A. m≥1 B. m>1且m≠5 C. m≥1且m≠5 D. m≠5
针对训练
已知关于x的一元二次方程x2-2mx-3m2+8m-4=0.
(1)求证:原方程恒有两个实数根.
(2)若方程的一个实数根为4,求m的值及方程的另一个根.
(3)若方程的两个实数根一个小于5,另一个大于2,求m的取值范围.(只分析解题思路)
有实数根
考点四 一元二次方程的应用
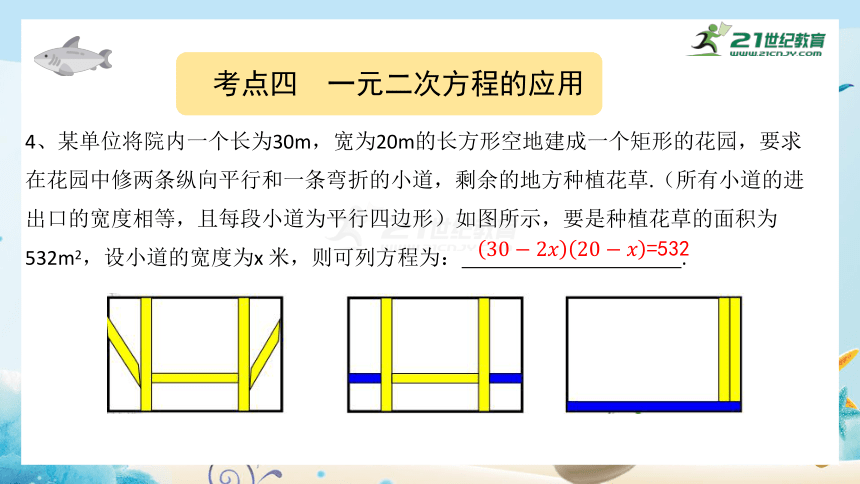
4、某单位将院内一个长为30m,宽为20m的长方形空地建成一个矩形的花园,要求在花园中修两条纵向平行和一条弯折的小道,剩余的地方种植花草.(所有小道的进出口的宽度相等,且每段小道为平行四边形)如图所示,要是种植花草的面积为532m2,设小道的宽度为x 米,则可列方程为: .
=532
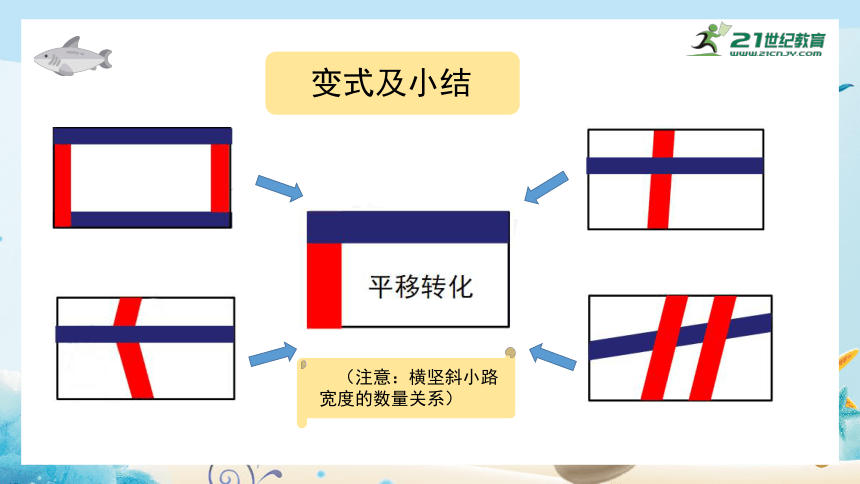
变式及小结
(注意:横坚斜小路宽度的数量关系)
考点四 一元二次方程的应用
5、新竹文具店以16元/支的价格购进一批钢笔,根据市场调查,如果以20元/支的价格销售,每月可以售出200支;而这种钢笔的售价每上涨1元就少卖10支.现在商店店主希望销售该种钢笔月利润为1350元,则该种钢笔该如何涨价?此时店主该进货多少?
分析
解答
考点四 一元二次方程的应用
6、如图,在Rt△ACB中,∠C=90°,BC=30cm,AC=40cm,点P、Q同时由A、B两点出发分别沿AC,BC方向向点C匀速运动,当点P移动到点C时停止,点Q也随之停止. 已知点P移动的速度是10cm/s,点Q移动的速度是5cm/s,几秒后△PCQ的面积为△ACB面积的?
拓展提高
7、新苑小区的物业管理部门为了美化环境,在小区靠墙的一侧设计了一处长方形花圃(墙长25m),三边外围用篱笆围起,栽上蝴蝶花,共用篱笆40m.
(1)花圃的面积能达到180 m2吗?
(2)花圃的面积能达到250 m2吗?
如果能,请你给出设计方案;如果不能,请说明理由.
(3)你能根据所学过的知识求出花圃的最大面积吗?此时,篱笆该怎样围?
知识框架
一元二次方程
一元二次方程的定义
一元二次方程的解及解法
根的判别式及根与系数的关系
一元二次方程的应用
概念:①一元;②二次;③整式方程.
一般形式:.
直接开方法
配方法
公式法
因式分解法
( ≥0)
根的判别式: △
根与系数的关系
面积问题、增长率问题
利润问题、动点、握手、送贺卡等问题
中考连接
1.(2013河南3题3分)方程=0的解是( )
B.
C. D.
2.(2018河南7题3分)下列一元二次方程中,有两个不相等实数根的是
( )
B.
C. D.
中考连接
3.(2017河南6题3分)方程2的根的情况是( )
有两个相等的实数根 B.有两个不相等的实数根
C. 只有一个实数根 D. 没有实数根
4.(2016河南11题3分)若关于的一元二次方程有两个不相等实数根,则的取值范围是 .
中考连接
5.(2015河南19题9分)已知关于的一元二次方程.
(1)求证:对于任意实数,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求的值及方程的另一个根.
布置作业
1、本节课中涉及的所有题目在课下进行分类整理,留作资料;
2、整理你见到的关于本章的新题型;
3、针对自己对本章的理解,每名同学出一份自命题试卷,要求时间在60分钟左右,重点突出,难度适宜,并配有答案.
谢谢!
(1)利润的表达形式有哪几种?
(2)本题中的等量关系是什么?
解:设涨价x元时,月利润可达1350元,则此时应进货支. 根据题意,得
解得
当x=11时,200-10x=200-10×11=90;
当x=5时,200-10x=200-10×5=150.
答:当每支钢笔涨价1元或5元时,月利润可达1350元.
当每支钢笔涨价1元时,应进货90支;当每支钢笔涨价5元时,应进货150支.
解:设垂直于墙的一边的篱笆长为x m.
(1)
解得(不合题意,舍去)
∴花圃的面积能达到180 m2,其中垂直于墙的一边的篱笆长为米.
(2)
∵△<0 ,∴方程无解.
∴花圃的面积达不到250m2.
(3)
∴花圃的最大面积为200 m2,垂直于墙的一边的篱笆长为10米.
解:设 t 秒后△PCQ的面积为△ACB面积的 .
由题意可得:AP=40-10t ,BQ=30-5t.
∵ ∠C=90°,BC=30cm,AC=40cm,∴ S△PCQ= S△ACB.
即 PC×CQ= × AC×BC.
∴ 30×40= ( 40-10t )(30-5t).
解得:t1=2 ,t2=8.
由题意可知:0≤t<4 ∴t=2.
答:2秒后△PCQ的面积为△ACB面积的
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第二章 一元二次方程回顾与思考
学习目标
1、通过课前自主学习,建构一元二次方程知识体系.
2、通过归纳本章习题,进行典型例题的解析.
3、能用一元二次方程解决一些简单的实际问题,体会方程是刻画现实问题的有效模型.
知识回顾
考点一 一元二次方程的定义
1、若关于x的方程(m-1)x2+mx-1=0是一元二次方程,则m的取值范围是( )
A. m≠1 B. m=1 C. m>1 D. m≠0
A
考点二 一元二次方程的解及解法
2、用简便方法解下列方程(先说岀适合的解法,并说明理由)
(1)2x2-3x-7=0 (2)9-x2=2x2-6x
(3)(x+1)(2-x)=2 (4)(3x-2)2=8
针对训练
(易错题)三角形两边长分别为3和6,第三边的长是方程x2-13+36=0的根,则该三角形的周长为( )
A.13 B.15 C.18 D.13或18
A
考点三 一元二次方程根的判别式及根与系数的关系
3、已知关于x的方程(m5)x2-4x-1=0有两个实数根,则m的取值范围是( )
A. m≥1 B. m>1且m≠5 C. m≥1且m≠5 D. m≠5
针对训练
已知关于x的一元二次方程x2-2mx-3m2+8m-4=0.
(1)求证:原方程恒有两个实数根.
(2)若方程的一个实数根为4,求m的值及方程的另一个根.
(3)若方程的两个实数根一个小于5,另一个大于2,求m的取值范围.(只分析解题思路)
有实数根
考点四 一元二次方程的应用
4、某单位将院内一个长为30m,宽为20m的长方形空地建成一个矩形的花园,要求在花园中修两条纵向平行和一条弯折的小道,剩余的地方种植花草.(所有小道的进出口的宽度相等,且每段小道为平行四边形)如图所示,要是种植花草的面积为532m2,设小道的宽度为x 米,则可列方程为: .
=532
变式及小结
(注意:横坚斜小路宽度的数量关系)
考点四 一元二次方程的应用
5、新竹文具店以16元/支的价格购进一批钢笔,根据市场调查,如果以20元/支的价格销售,每月可以售出200支;而这种钢笔的售价每上涨1元就少卖10支.现在商店店主希望销售该种钢笔月利润为1350元,则该种钢笔该如何涨价?此时店主该进货多少?
分析
解答
考点四 一元二次方程的应用
6、如图,在Rt△ACB中,∠C=90°,BC=30cm,AC=40cm,点P、Q同时由A、B两点出发分别沿AC,BC方向向点C匀速运动,当点P移动到点C时停止,点Q也随之停止. 已知点P移动的速度是10cm/s,点Q移动的速度是5cm/s,几秒后△PCQ的面积为△ACB面积的?
拓展提高
7、新苑小区的物业管理部门为了美化环境,在小区靠墙的一侧设计了一处长方形花圃(墙长25m),三边外围用篱笆围起,栽上蝴蝶花,共用篱笆40m.
(1)花圃的面积能达到180 m2吗?
(2)花圃的面积能达到250 m2吗?
如果能,请你给出设计方案;如果不能,请说明理由.
(3)你能根据所学过的知识求出花圃的最大面积吗?此时,篱笆该怎样围?
知识框架
一元二次方程
一元二次方程的定义
一元二次方程的解及解法
根的判别式及根与系数的关系
一元二次方程的应用
概念:①一元;②二次;③整式方程.
一般形式:.
直接开方法
配方法
公式法
因式分解法
( ≥0)
根的判别式: △
根与系数的关系
面积问题、增长率问题
利润问题、动点、握手、送贺卡等问题
中考连接
1.(2013河南3题3分)方程=0的解是( )
B.
C. D.
2.(2018河南7题3分)下列一元二次方程中,有两个不相等实数根的是
( )
B.
C. D.
中考连接
3.(2017河南6题3分)方程2的根的情况是( )
有两个相等的实数根 B.有两个不相等的实数根
C. 只有一个实数根 D. 没有实数根
4.(2016河南11题3分)若关于的一元二次方程有两个不相等实数根,则的取值范围是 .
中考连接
5.(2015河南19题9分)已知关于的一元二次方程.
(1)求证:对于任意实数,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求的值及方程的另一个根.
布置作业
1、本节课中涉及的所有题目在课下进行分类整理,留作资料;
2、整理你见到的关于本章的新题型;
3、针对自己对本章的理解,每名同学出一份自命题试卷,要求时间在60分钟左右,重点突出,难度适宜,并配有答案.
谢谢!
(1)利润的表达形式有哪几种?
(2)本题中的等量关系是什么?
解:设涨价x元时,月利润可达1350元,则此时应进货支. 根据题意,得
解得
当x=11时,200-10x=200-10×11=90;
当x=5时,200-10x=200-10×5=150.
答:当每支钢笔涨价1元或5元时,月利润可达1350元.
当每支钢笔涨价1元时,应进货90支;当每支钢笔涨价5元时,应进货150支.
解:设垂直于墙的一边的篱笆长为x m.
(1)
解得(不合题意,舍去)
∴花圃的面积能达到180 m2,其中垂直于墙的一边的篱笆长为米.
(2)
∵△<0 ,∴方程无解.
∴花圃的面积达不到250m2.
(3)
∴花圃的最大面积为200 m2,垂直于墙的一边的篱笆长为10米.
解:设 t 秒后△PCQ的面积为△ACB面积的 .
由题意可得:AP=40-10t ,BQ=30-5t.
∵ ∠C=90°,BC=30cm,AC=40cm,∴ S△PCQ= S△ACB.
即 PC×CQ= × AC×BC.
∴ 30×40= ( 40-10t )(30-5t).
解得:t1=2 ,t2=8.
由题意可知:0≤t<4 ∴t=2.
答:2秒后△PCQ的面积为△ACB面积的
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
