2.1单式折线统计图的认识和应用 教案 五年级数学下册-苏教版
文档属性
| 名称 | 2.1单式折线统计图的认识和应用 教案 五年级数学下册-苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 492.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 11:29:21 | ||
图片预览

文档简介
册2.1单式折线统计图的认识和应用
教学目标
1、使学生结合实际问题认识单式折线统计图,了解折线统计图表示数据的基本方法和特点,能看懂折线统计图表示的数据信息。会用折线统计图表示相关的数据。
2、使学生在读图、画图,以及对图中信息进行分析、比较,基于数据作出判断、预测等活动中,进一步积累统计活动经验,感受数据对于分析和解决问题的意义,发展数据分析观念。
3、使学生在统计活动过程中,进一步感受数学与现实生活的联系,提高对统计活动的兴趣,增强动手实践、合作交流的意识。
课时安排
1课时
教学重点
结合实际问题认识单式折线统计图,了解折线统计图表示数据的基本方法和特点,能看懂折线统计图表示的数据信息。会用折线统计图表示相关的数据。
四、教学难点
结合实际问题认识单式折线统计图,了解折线统计图表示数据的基本方法和特点,能看懂折线统计图表示的数据信息。会用折线统计图表示相关的数据。
五、教学过程
(一)导入新课
出示例1:张小楠把自己6——12岁生日测得的身高数据制成了统计表。
张小楠6——12岁身高情况统计表
2012年6月
你从中能读出哪些数学信息?
讲授新课
师生交流数学信息后小结:
表中有两组数据,一组是年龄,一组是身高,年龄按从小到大的次序连续变化,身高按从矮到高的次序连续变化的。
在小学阶段,身高是随着年龄的增长而增长的。
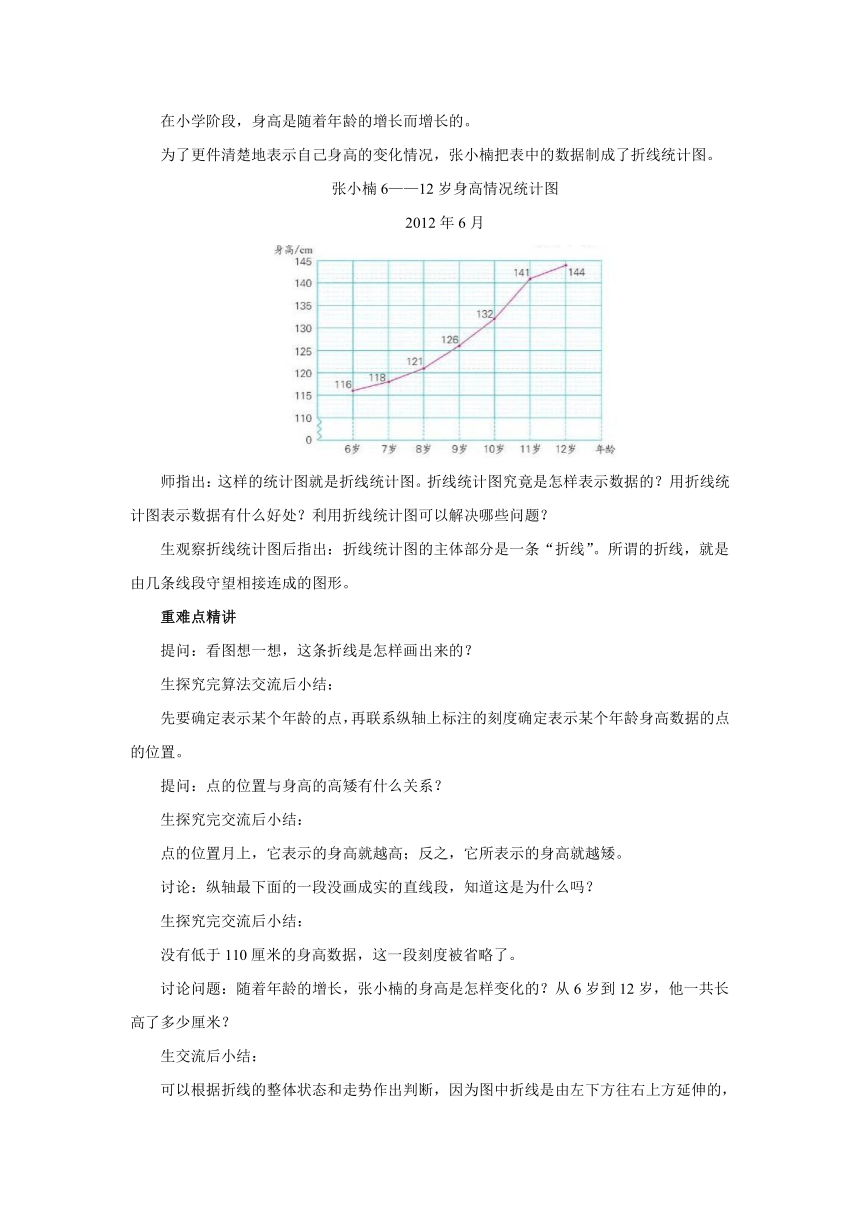
为了更件清楚地表示自己身高的变化情况,张小楠把表中的数据制成了折线统计图。
张小楠6——12岁身高情况统计图
2012年6月
师指出:这样的统计图就是折线统计图。折线统计图究竟是怎样表示数据的?用折线统计图表示数据有什么好处?利用折线统计图可以解决哪些问题?
生观察折线统计图后指出:折线统计图的主体部分是一条“折线”。所谓的折线,就是由几条线段守望相接连成的图形。
重难点精讲
提问:看图想一想,这条折线是怎样画出来的?
生探究完算法交流后小结:
先要确定表示某个年龄的点,再联系纵轴上标注的刻度确定表示某个年龄身高数据的点的位置。
提问:点的位置与身高的高矮有什么关系?
生探究完交流后小结:
点的位置月上,它表示的身高就越高;反之,它所表示的身高就越矮。
讨论:纵轴最下面的一段没画成实的直线段,知道这是为什么吗?
生探究完交流后小结:
没有低于110厘米的身高数据,这一段刻度被省略了。
讨论问题:随着年龄的增长,张小楠的身高是怎样变化的?从6岁到12岁,他一共长高了多少厘米?
生交流后小结:
可以根据折线的整体状态和走势作出判断,因为图中折线是由左下方往右上方延伸的,所以它就表示身高是随着年龄的增长而增长的。
提问:从图上看,哪一年张小楠的身高增长的最快?你是怎样看出来的?
生交流后小结:
看折线中的某一部分的倾斜程度。某段折线倾斜程度越大,说明相应两个年龄之间的身高增长越快;某段折线倾斜程度越小,说明相应两个年龄之间的身高增长越慢。
提问:估计一下,张小楠13岁生日时的身高大约是多少厘米?
生交流后小结:
①张小楠13岁生日时的身高一定超过144厘米;②至于超过的厘米数,估计位5——5厘米较为合适;③由于影响身高变化的因素非常多少,所以上面的预测带有不确定性。
通过上面的学习,你有什么收获和体会?
从折线统计图中不仅能够看出数量的多少,而且能够更清楚地看出数量的增减变化情况。
在折线统计图中,某段折线倾斜程度越大,说明相应数据增长越快;某段折线倾斜程度越小,说明数据增长越慢。
归纳小结
通过刚才的探究,你能说说你的收获吗?
师生交流后小结:
从折线统计图中不仅能够看出数量的多少,而且能够更清楚地看出数量的增减变化情况。
在折线统计图中,某段折线倾斜程度越大,说明相应数据增长越快;某段折线倾斜程度越小,说明数据增长越慢。
课堂检测
1、你上小学后身高是怎样变化的?收集自己从一年级开始每年体检的身高数据,先填写统计表,再完成折线统计图。
讨论下面的问题:
从一年级到五年级,你一共长高了多少厘米?从哪个年级到哪个年级,你的身高增长最快?
全班同学中,谁的身高长得最快?身高增长最快的时间大多集中在哪个年级到哪个年级。
一位病人某天7——23时的体温变化情况如下图:
病人的体温在哪个时间段不断上升?从几时到几时上升最快?
病人的体温从几时起开始下降?从几时起趋于平稳?
从图中你还能知道什么?
板书设计
单式折线统计图的认识和应用
从折线统计图中不仅能够看出数量的多少,而且能够更清楚地看出数量的增减变化情况。
在折线统计图中,某段折线倾斜程度越大,说明相应数据增长越快;某段折线倾斜程度越小,说明数据增长越慢。
作业布置
1、你上小学后体重是怎样变化的?收集自己从一年级开始每年体检的体重数据,先填写统计表,再完成折线统计图。
2、预习第23、24页的有关内容。
教学反思
教学目标
1、使学生结合实际问题认识单式折线统计图,了解折线统计图表示数据的基本方法和特点,能看懂折线统计图表示的数据信息。会用折线统计图表示相关的数据。
2、使学生在读图、画图,以及对图中信息进行分析、比较,基于数据作出判断、预测等活动中,进一步积累统计活动经验,感受数据对于分析和解决问题的意义,发展数据分析观念。
3、使学生在统计活动过程中,进一步感受数学与现实生活的联系,提高对统计活动的兴趣,增强动手实践、合作交流的意识。
课时安排
1课时
教学重点
结合实际问题认识单式折线统计图,了解折线统计图表示数据的基本方法和特点,能看懂折线统计图表示的数据信息。会用折线统计图表示相关的数据。
四、教学难点
结合实际问题认识单式折线统计图,了解折线统计图表示数据的基本方法和特点,能看懂折线统计图表示的数据信息。会用折线统计图表示相关的数据。
五、教学过程
(一)导入新课
出示例1:张小楠把自己6——12岁生日测得的身高数据制成了统计表。
张小楠6——12岁身高情况统计表
2012年6月
你从中能读出哪些数学信息?
讲授新课
师生交流数学信息后小结:
表中有两组数据,一组是年龄,一组是身高,年龄按从小到大的次序连续变化,身高按从矮到高的次序连续变化的。
在小学阶段,身高是随着年龄的增长而增长的。
为了更件清楚地表示自己身高的变化情况,张小楠把表中的数据制成了折线统计图。
张小楠6——12岁身高情况统计图
2012年6月
师指出:这样的统计图就是折线统计图。折线统计图究竟是怎样表示数据的?用折线统计图表示数据有什么好处?利用折线统计图可以解决哪些问题?
生观察折线统计图后指出:折线统计图的主体部分是一条“折线”。所谓的折线,就是由几条线段守望相接连成的图形。
重难点精讲
提问:看图想一想,这条折线是怎样画出来的?
生探究完算法交流后小结:
先要确定表示某个年龄的点,再联系纵轴上标注的刻度确定表示某个年龄身高数据的点的位置。
提问:点的位置与身高的高矮有什么关系?
生探究完交流后小结:
点的位置月上,它表示的身高就越高;反之,它所表示的身高就越矮。
讨论:纵轴最下面的一段没画成实的直线段,知道这是为什么吗?
生探究完交流后小结:
没有低于110厘米的身高数据,这一段刻度被省略了。
讨论问题:随着年龄的增长,张小楠的身高是怎样变化的?从6岁到12岁,他一共长高了多少厘米?
生交流后小结:
可以根据折线的整体状态和走势作出判断,因为图中折线是由左下方往右上方延伸的,所以它就表示身高是随着年龄的增长而增长的。
提问:从图上看,哪一年张小楠的身高增长的最快?你是怎样看出来的?
生交流后小结:
看折线中的某一部分的倾斜程度。某段折线倾斜程度越大,说明相应两个年龄之间的身高增长越快;某段折线倾斜程度越小,说明相应两个年龄之间的身高增长越慢。
提问:估计一下,张小楠13岁生日时的身高大约是多少厘米?
生交流后小结:
①张小楠13岁生日时的身高一定超过144厘米;②至于超过的厘米数,估计位5——5厘米较为合适;③由于影响身高变化的因素非常多少,所以上面的预测带有不确定性。
通过上面的学习,你有什么收获和体会?
从折线统计图中不仅能够看出数量的多少,而且能够更清楚地看出数量的增减变化情况。
在折线统计图中,某段折线倾斜程度越大,说明相应数据增长越快;某段折线倾斜程度越小,说明数据增长越慢。
归纳小结
通过刚才的探究,你能说说你的收获吗?
师生交流后小结:
从折线统计图中不仅能够看出数量的多少,而且能够更清楚地看出数量的增减变化情况。
在折线统计图中,某段折线倾斜程度越大,说明相应数据增长越快;某段折线倾斜程度越小,说明数据增长越慢。
课堂检测
1、你上小学后身高是怎样变化的?收集自己从一年级开始每年体检的身高数据,先填写统计表,再完成折线统计图。
讨论下面的问题:
从一年级到五年级,你一共长高了多少厘米?从哪个年级到哪个年级,你的身高增长最快?
全班同学中,谁的身高长得最快?身高增长最快的时间大多集中在哪个年级到哪个年级。
一位病人某天7——23时的体温变化情况如下图:
病人的体温在哪个时间段不断上升?从几时到几时上升最快?
病人的体温从几时起开始下降?从几时起趋于平稳?
从图中你还能知道什么?
板书设计
单式折线统计图的认识和应用
从折线统计图中不仅能够看出数量的多少,而且能够更清楚地看出数量的增减变化情况。
在折线统计图中,某段折线倾斜程度越大,说明相应数据增长越快;某段折线倾斜程度越小,说明数据增长越慢。
作业布置
1、你上小学后体重是怎样变化的?收集自己从一年级开始每年体检的体重数据,先填写统计表,再完成折线统计图。
2、预习第23、24页的有关内容。
教学反思
