6.4圆的周长 教案 五年级数学下册 苏教版
文档属性
| 名称 | 6.4圆的周长 教案 五年级数学下册 苏教版 |  | |
| 格式 | doc | ||
| 文件大小 | 313.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-28 14:29:35 | ||
图片预览

文档简介
6.4圆的周长
教学目标
在观察、操作、测量等活动中,经历探索圆周率以及总结圆周长公式的过程。
认识圆周率,理解并掌握圆的周长公式,能运用周长公式正确进行计算。
体验数学与日常生活的密切联系,了解圆周率的探索历史,激发民族自豪感。
课时安排
1课时
教学重点
认识圆周率,理解并掌握圆的周长公式,能运用周长公式正确进行计算。
教学难点
认识圆周率,理解并掌握圆的周长公式,能运用周长公式正确进行计算。
五、教学过程
(一)导入新课
出示例4:下面3个自行车车轮各滚动一周,哪个车轮行的路程比较长?
你从中读出什么数学信息?
讲授新课
师生交流数学信息,
车轮一周的长度是车轮的周长。
探究问题:比较3个车轮的直径和周长,你有什么发现?
生探究后交流展示:
小结:车轮的直径越长,周长就越长。
重难点精讲
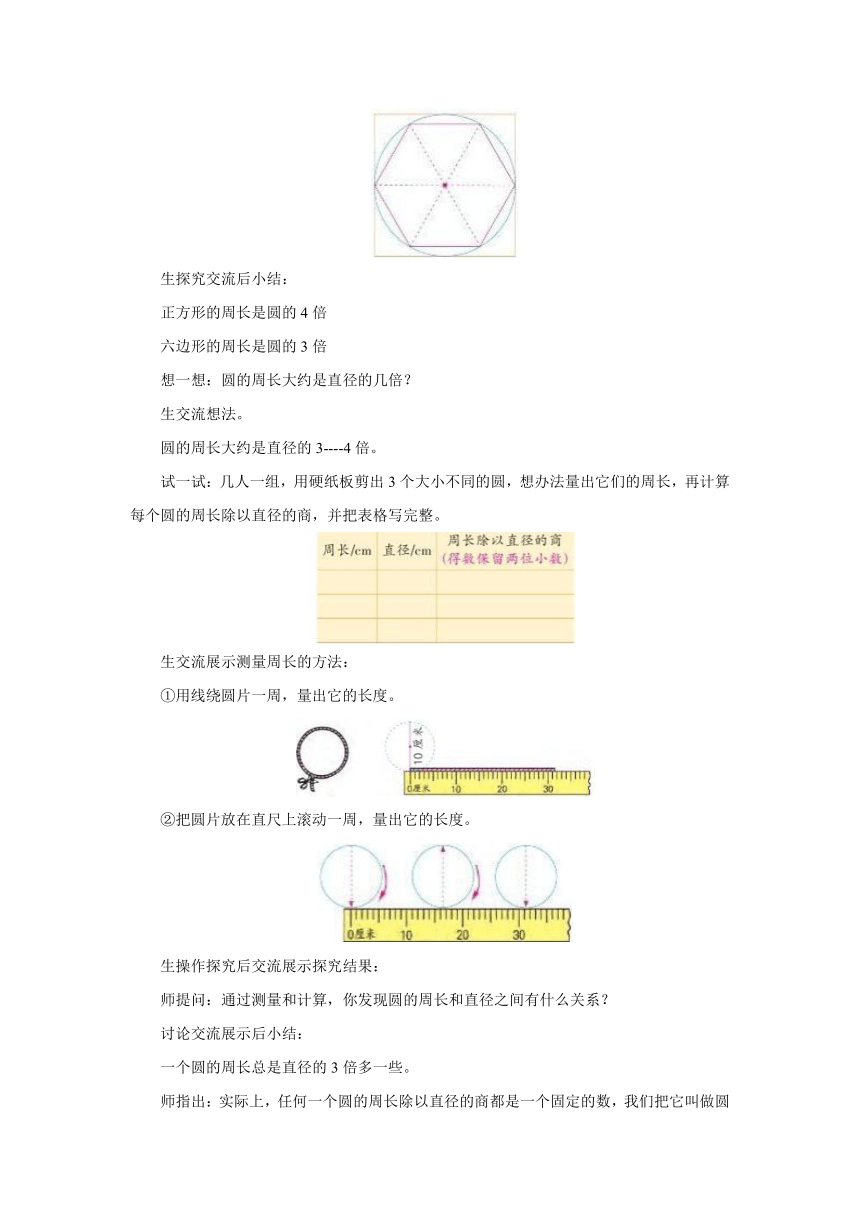
出示例5:如图,在正方形内画一个最大的圆。你知道正方形的周长是圆的几倍吗?
在圆内画一个正六边形。六边形的顶点都在圆上,你知道六边形的周长是圆的几倍吗?
生探究交流后小结:
正方形的周长是圆的4倍
六边形的周长是圆的3倍
想一想:圆的周长大约是直径的几倍?
生交流想法。
圆的周长大约是直径的3----4倍。
试一试:几人一组,用硬纸板剪出3个大小不同的圆,想办法量出它们的周长,再计算每个圆的周长除以直径的商,并把表格写完整。
生交流展示测量周长的方法:
①用线绕圆片一周,量出它的长度。
②把圆片放在直尺上滚动一周,量出它的长度。
生操作探究后交流展示探究结果:
师提问:通过测量和计算,你发现圆的周长和直径之间有什么关系?
讨论交流展示后小结:
一个圆的周长总是直径的3倍多一些。
师指出:实际上,任何一个圆的周长除以直径的商都是一个固定的数,我们把它叫做圆周率,用字母π表示。π是一个无限不循环的小数。
π=3.141592653……
在计算时,一般保留两位小数,取它的近似值3.14。
如果用C表示圆的周长,那么周长C与直径d或半径r的关系是:
C=πd 或 C=2πr
试一试:例4中的三种车轮的周长大约各是多少厘米?算一算。
生探究后交流:
车轮1: 3.14×66=207.24(米)
车轮2: 3.14×61=191.54(米)
车轮3: 3.14×56=175.84(米)
归纳小结
通过刚才的探究,你能说说你的收获吗?
师生交流后小结:
任何圆的周长总是它的直径的3倍多一些,这个倍数是一个固定不变的数,我们把它叫做圆周率,用字母π表示。它是一个无限的不循环的小数。
计算时一般只取它的近似值;π≈3.14。
如果用C表示圆的周长,则C=πd 或C=2πr
)随堂检测
一个圆形喷水池的半径是14米。它的周长是多少米?
计算下面各圆的周长。
计算各圆的周长。
d=5cm d=3.5dm r=4cm r=1.2cm
一种汽车车轮的直径是0.6米。它在公路上转一周前进多少米?
摩天轮的半径是10米,坐着它转动一周,大约在空中转过多少米?
板书设计
圆的周长
任何圆的周长总是它的直径的3倍多一些,这个倍数是一个固定不变的数,我们把它叫做圆周率,用字母π表示。它是一个无限的不循环的小数。
计算时一般只取它的近似值;π≈3.14。
如果用C表示圆的周长,则C=πd 或C=2πr
作业布置
1、调查并计算
2、预习第93页有关内容。
八、教学反思
教学目标
在观察、操作、测量等活动中,经历探索圆周率以及总结圆周长公式的过程。
认识圆周率,理解并掌握圆的周长公式,能运用周长公式正确进行计算。
体验数学与日常生活的密切联系,了解圆周率的探索历史,激发民族自豪感。
课时安排
1课时
教学重点
认识圆周率,理解并掌握圆的周长公式,能运用周长公式正确进行计算。
教学难点
认识圆周率,理解并掌握圆的周长公式,能运用周长公式正确进行计算。
五、教学过程
(一)导入新课
出示例4:下面3个自行车车轮各滚动一周,哪个车轮行的路程比较长?
你从中读出什么数学信息?
讲授新课
师生交流数学信息,
车轮一周的长度是车轮的周长。
探究问题:比较3个车轮的直径和周长,你有什么发现?
生探究后交流展示:
小结:车轮的直径越长,周长就越长。
重难点精讲
出示例5:如图,在正方形内画一个最大的圆。你知道正方形的周长是圆的几倍吗?
在圆内画一个正六边形。六边形的顶点都在圆上,你知道六边形的周长是圆的几倍吗?
生探究交流后小结:
正方形的周长是圆的4倍
六边形的周长是圆的3倍
想一想:圆的周长大约是直径的几倍?
生交流想法。
圆的周长大约是直径的3----4倍。
试一试:几人一组,用硬纸板剪出3个大小不同的圆,想办法量出它们的周长,再计算每个圆的周长除以直径的商,并把表格写完整。
生交流展示测量周长的方法:
①用线绕圆片一周,量出它的长度。
②把圆片放在直尺上滚动一周,量出它的长度。
生操作探究后交流展示探究结果:
师提问:通过测量和计算,你发现圆的周长和直径之间有什么关系?
讨论交流展示后小结:
一个圆的周长总是直径的3倍多一些。
师指出:实际上,任何一个圆的周长除以直径的商都是一个固定的数,我们把它叫做圆周率,用字母π表示。π是一个无限不循环的小数。
π=3.141592653……
在计算时,一般保留两位小数,取它的近似值3.14。
如果用C表示圆的周长,那么周长C与直径d或半径r的关系是:
C=πd 或 C=2πr
试一试:例4中的三种车轮的周长大约各是多少厘米?算一算。
生探究后交流:
车轮1: 3.14×66=207.24(米)
车轮2: 3.14×61=191.54(米)
车轮3: 3.14×56=175.84(米)
归纳小结
通过刚才的探究,你能说说你的收获吗?
师生交流后小结:
任何圆的周长总是它的直径的3倍多一些,这个倍数是一个固定不变的数,我们把它叫做圆周率,用字母π表示。它是一个无限的不循环的小数。
计算时一般只取它的近似值;π≈3.14。
如果用C表示圆的周长,则C=πd 或C=2πr
)随堂检测
一个圆形喷水池的半径是14米。它的周长是多少米?
计算下面各圆的周长。
计算各圆的周长。
d=5cm d=3.5dm r=4cm r=1.2cm
一种汽车车轮的直径是0.6米。它在公路上转一周前进多少米?
摩天轮的半径是10米,坐着它转动一周,大约在空中转过多少米?
板书设计
圆的周长
任何圆的周长总是它的直径的3倍多一些,这个倍数是一个固定不变的数,我们把它叫做圆周率,用字母π表示。它是一个无限的不循环的小数。
计算时一般只取它的近似值;π≈3.14。
如果用C表示圆的周长,则C=πd 或C=2πr
作业布置
1、调查并计算
2、预习第93页有关内容。
八、教学反思
