5.3.2 命题、定理、证明 同步训练 2021-2022学年 人教版 七年级数学下册(word版 含答案)
文档属性
| 名称 | 5.3.2 命题、定理、证明 同步训练 2021-2022学年 人教版 七年级数学下册(word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 145.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 13:58:27 | ||
图片预览



文档简介
2022年春人教版初中七年级数学下册 同步训练
班级 姓名
第五章 相交线与平行线
5.3 平行线的性质
5.3.2 命题、定理、证明
测试时间:10分钟
一、选择题
1.(2021广西南宁兴宁三美学校期末)下列说法正确的是( )
A.经过一点有且只有一条直线与已知直线平行
B.直线外一点到这条直线的垂线段,叫做点到直线的距离
C.同一平面内,不相交的两条直线是平行线
D.“相等的角是对顶角”是真命题
2.(2021河南安阳滑县期末)下列说法中,属于真命题的是( )
A.垂线最短
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.相等的角一定是对顶角
D.两直线相交,邻补角相等
3.把命题“同角的余角相等”改写成“如果……那么……”的形式,正确的是( )
A.如果是同角,那么余角相等
B.如果两个角相等,那么这两个角是同一个角的余角
C.如果是同角的余角,那么相等
D.如果两个角是同一个角的余角,那么这两个角相等
4.(2021江西九江期末)对于命题“若a2>b2,则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )
A.a=3,b=2 B.a=-1,b=3
C.a=-3,b=2 D.a=3,b=-1
5.下列句子中命题的个数是( )
①你喜欢数学吗?
②熊猫没有翅膀;
③任何一个三角形一定有直角;
④作线段AB=CD;
⑤连接AC;
⑥无论n是怎样的自然数,式子n2-n+11的值都是质数;
⑦如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
A.4 B.5 C.6 D.7
6.如图,直线a,b被直线c所截,下列说法正确的是( )
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180° 时,一定有a∥b
二、填空题
7.“直角都相等”的题设是 ,结论是 .
8.把“垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式是 .
9.(2021安徽黄山期末)下列三个命题:
①对顶角相等;②同旁内角互补;③两直线平行,同位角相等.
其中是假命题的有 .(填序号)
10.命题“若a2=b2,则a=b.”是 (填“真命题”或“假命题”).
三、解答题
11.把下列命题写成“如果……那么……”的形式,并判断其真假.
(1)等角的补角相等;
(2)不相等的角不是对顶角;
(3)相等的角是内错角.
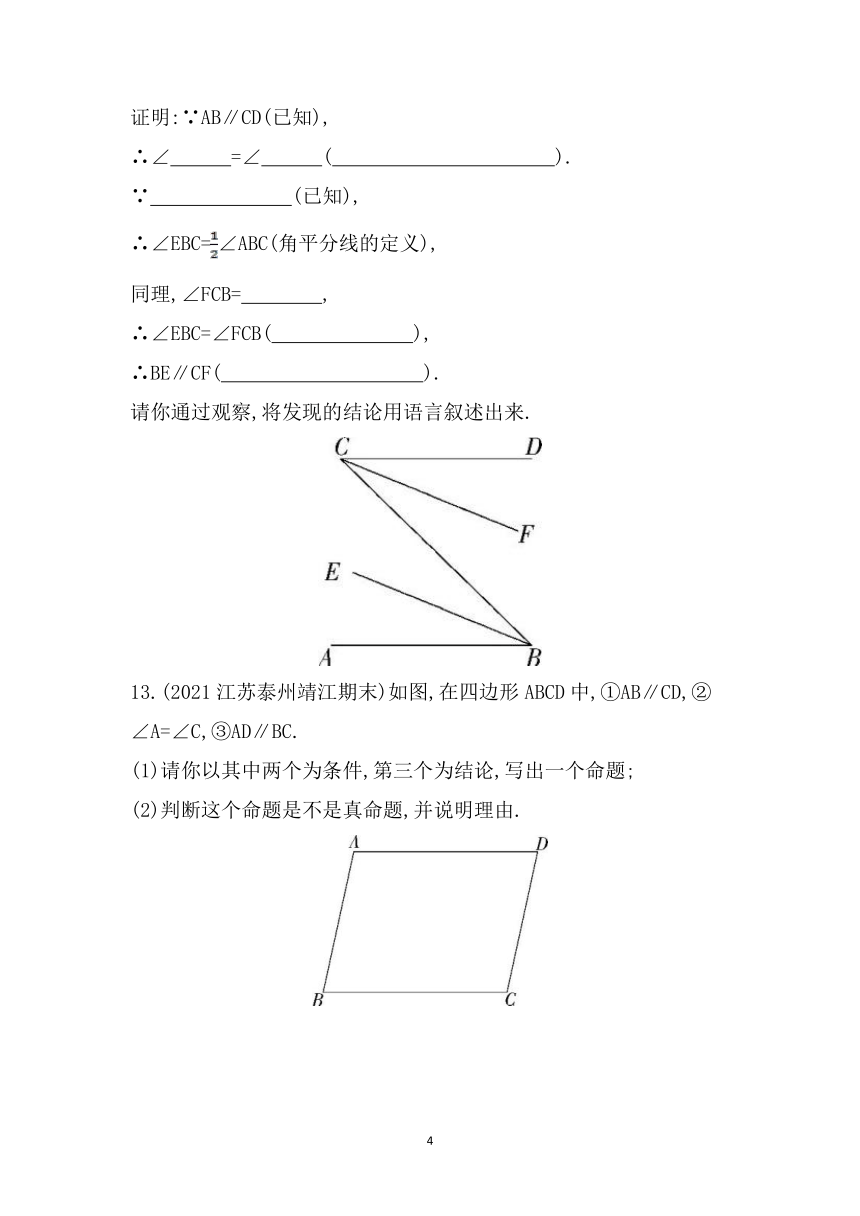
12.(2021江苏扬州江都月考)在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式).
如图,已知直线AB∥直线CD,射线BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
证明:∵AB∥CD(已知),
∴∠ =∠ ( ).
∵ (已知),
∴∠EBC=∠ABC(角平分线的定义),
同理,∠FCB= ,
∴∠EBC=∠FCB( ),
∴BE∥CF( ).
请你通过观察,将发现的结论用语言叙述出来.
13.(2021江苏泰州靖江期末)如图,在四边形ABCD中,①AB∥CD,②∠A=∠C,③AD∥BC.
(1)请你以其中两个为条件,第三个为结论,写出一个命题;
(2)判断这个命题是不是真命题,并说明理由.
14.[2020春·港南区期末]如图 ,已知∠A=∠ADE,∠C=∠E.
(1)若∠EDC=3∠C,求∠C的度数;
(2)求证:BE∥CD.
15.有一天,李明同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图5 3 20①),他用鼠标左键点住点E,拖动后,分别得到如图5 3 20②,③,④等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着李明同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
(1)你能探究出图①到图④各图中的∠B,∠D与∠BED之间的关系吗?
(2)请从所得的四个关系中,选一个说明它成立的理由.
一、选择题
1.答案 C A.经过直线外一点有且只有一条直线与已知直线平行,故该选项错误;
B.直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故该选项错误;
C.同一平面内,不相交的两条直线是平行线,正确;
D.“相等的角是对顶角”是假命题,故该选项错误.故选C.
2.答案 B 垂线段最短,故A不是真命题;
在同一平面内,过一点有且只有一条直线与已知直线垂直,故B为真命题;
对顶角一定相等,但相等的角并不一定都是对顶角,故C不是真命题;
由邻补角的定义可知,两直线相交,邻补角互补,故D不是真命题.故选B.
3.答案 D 命题“同角的余角相等”改写成“如果……那么……”的形式为如果两个角是同一个角的余角,那么这两个角相等.故选D.
4.答案 C 说明命题为假命题,即a、b的值满足a2>b2,但a>b不成立,把四个选项中的a、b的值分别代入验证即可判断,选项C符合题意.
5. 答案 A
6. 答案 D
二、填空题
7.答案 两个角是直角;这两个角相等
8.答案 如果两条直线垂直于同一条直线,那么这两条直线平行
9.答案 ②
解析 ①对顶角相等,是真命题;
②两直线平行,同旁内角互补,原命题是假命题;
③两直线平行,同位角相等,是真命题.
故答案为②.
10. 答案 假命题
三、解答题
11.解析 (1)如果两个角分别是两个相等的角的补角,那么这两个角相等.是真命题.
(2)如果两个角不相等,那么这两个角不是对顶角.是真命题.
(3)如果两个角相等,那么这两个角是内错角.是假命题.
12.解析 证明:∵AB∥CD(已知),
∴∠ABC=∠DCB(两直线平行,内错角相等).
∵BE平分∠ABC(已知),
∴∠EBC=∠ABC(角平分线的定义),
同理,∠FCB=∠DCB,
∴∠EBC=∠FCB(等量代换),
∴BE∥CF(内错角相等,两直线平行).
通过观察,发现的结论如下:两条平行线被第三条直线所截,所形成的内错角的平分线互相平行.
13.解析 答案不唯一.
(1)如果AB∥CD,∠A=∠C,那么AD∥BC.
(2)这个命题是真命题,
理由:∵AB∥CD,
∴∠B+∠C=180°,
∵∠A=∠C,
∴∠B+∠A=180°,
∴AD∥BC.
14. (1)解:∵∠A=∠ADE,∴AC∥DE,
∴∠EDC+∠C=180°.
又∵∠EDC=3∠C,∴4∠C=180°,即∠C=45°.
(2)证明:∵AC∥DE,∴∠E=∠ABE.
又∵∠C=∠E,∴∠C=∠ABE,∴BE∥CD.
15. 解:(1)①∠B+∠D=∠BED;②∠B+∠D+∠BED=360°;③∠ABE=∠BED+∠D;④∠B=∠D+∠BED.
(2)选择①.理由如下:
如答图①,过点E作EF∥AB.
∵AB∥CD,∴EF∥CD,
∴∠B=∠BEF,∠D=∠DEF,
∴∠BED=∠BEF+∠DEF=∠B+∠D.
选择②.理由如下:
如答图②,过点E作EF∥AB.
∵AB∥CD,∴EF∥CD,
∴∠B+∠BEF=180°,∠D+∠DEF=180°,
∴∠B+∠BED+∠D=180°+180°=360°.
选择③.理由如下:
如答图③,延长AB交DE于点F.
∵AB∥CD,∴∠D=∠BFE.
∵∠ABE是△BEF的外角,
∴∠ABE=∠BEF+∠BFE=∠BED+∠D.
1
班级 姓名
第五章 相交线与平行线
5.3 平行线的性质
5.3.2 命题、定理、证明
测试时间:10分钟
一、选择题
1.(2021广西南宁兴宁三美学校期末)下列说法正确的是( )
A.经过一点有且只有一条直线与已知直线平行
B.直线外一点到这条直线的垂线段,叫做点到直线的距离
C.同一平面内,不相交的两条直线是平行线
D.“相等的角是对顶角”是真命题
2.(2021河南安阳滑县期末)下列说法中,属于真命题的是( )
A.垂线最短
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.相等的角一定是对顶角
D.两直线相交,邻补角相等
3.把命题“同角的余角相等”改写成“如果……那么……”的形式,正确的是( )
A.如果是同角,那么余角相等
B.如果两个角相等,那么这两个角是同一个角的余角
C.如果是同角的余角,那么相等
D.如果两个角是同一个角的余角,那么这两个角相等
4.(2021江西九江期末)对于命题“若a2>b2,则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )
A.a=3,b=2 B.a=-1,b=3
C.a=-3,b=2 D.a=3,b=-1
5.下列句子中命题的个数是( )
①你喜欢数学吗?
②熊猫没有翅膀;
③任何一个三角形一定有直角;
④作线段AB=CD;
⑤连接AC;
⑥无论n是怎样的自然数,式子n2-n+11的值都是质数;
⑦如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
A.4 B.5 C.6 D.7
6.如图,直线a,b被直线c所截,下列说法正确的是( )
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180° 时,一定有a∥b
二、填空题
7.“直角都相等”的题设是 ,结论是 .
8.把“垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式是 .
9.(2021安徽黄山期末)下列三个命题:
①对顶角相等;②同旁内角互补;③两直线平行,同位角相等.
其中是假命题的有 .(填序号)
10.命题“若a2=b2,则a=b.”是 (填“真命题”或“假命题”).
三、解答题
11.把下列命题写成“如果……那么……”的形式,并判断其真假.
(1)等角的补角相等;
(2)不相等的角不是对顶角;
(3)相等的角是内错角.
12.(2021江苏扬州江都月考)在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式).
如图,已知直线AB∥直线CD,射线BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
证明:∵AB∥CD(已知),
∴∠ =∠ ( ).
∵ (已知),
∴∠EBC=∠ABC(角平分线的定义),
同理,∠FCB= ,
∴∠EBC=∠FCB( ),
∴BE∥CF( ).
请你通过观察,将发现的结论用语言叙述出来.
13.(2021江苏泰州靖江期末)如图,在四边形ABCD中,①AB∥CD,②∠A=∠C,③AD∥BC.
(1)请你以其中两个为条件,第三个为结论,写出一个命题;
(2)判断这个命题是不是真命题,并说明理由.
14.[2020春·港南区期末]如图 ,已知∠A=∠ADE,∠C=∠E.
(1)若∠EDC=3∠C,求∠C的度数;
(2)求证:BE∥CD.
15.有一天,李明同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图5 3 20①),他用鼠标左键点住点E,拖动后,分别得到如图5 3 20②,③,④等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着李明同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
(1)你能探究出图①到图④各图中的∠B,∠D与∠BED之间的关系吗?
(2)请从所得的四个关系中,选一个说明它成立的理由.
一、选择题
1.答案 C A.经过直线外一点有且只有一条直线与已知直线平行,故该选项错误;
B.直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故该选项错误;
C.同一平面内,不相交的两条直线是平行线,正确;
D.“相等的角是对顶角”是假命题,故该选项错误.故选C.
2.答案 B 垂线段最短,故A不是真命题;
在同一平面内,过一点有且只有一条直线与已知直线垂直,故B为真命题;
对顶角一定相等,但相等的角并不一定都是对顶角,故C不是真命题;
由邻补角的定义可知,两直线相交,邻补角互补,故D不是真命题.故选B.
3.答案 D 命题“同角的余角相等”改写成“如果……那么……”的形式为如果两个角是同一个角的余角,那么这两个角相等.故选D.
4.答案 C 说明命题为假命题,即a、b的值满足a2>b2,但a>b不成立,把四个选项中的a、b的值分别代入验证即可判断,选项C符合题意.
5. 答案 A
6. 答案 D
二、填空题
7.答案 两个角是直角;这两个角相等
8.答案 如果两条直线垂直于同一条直线,那么这两条直线平行
9.答案 ②
解析 ①对顶角相等,是真命题;
②两直线平行,同旁内角互补,原命题是假命题;
③两直线平行,同位角相等,是真命题.
故答案为②.
10. 答案 假命题
三、解答题
11.解析 (1)如果两个角分别是两个相等的角的补角,那么这两个角相等.是真命题.
(2)如果两个角不相等,那么这两个角不是对顶角.是真命题.
(3)如果两个角相等,那么这两个角是内错角.是假命题.
12.解析 证明:∵AB∥CD(已知),
∴∠ABC=∠DCB(两直线平行,内错角相等).
∵BE平分∠ABC(已知),
∴∠EBC=∠ABC(角平分线的定义),
同理,∠FCB=∠DCB,
∴∠EBC=∠FCB(等量代换),
∴BE∥CF(内错角相等,两直线平行).
通过观察,发现的结论如下:两条平行线被第三条直线所截,所形成的内错角的平分线互相平行.
13.解析 答案不唯一.
(1)如果AB∥CD,∠A=∠C,那么AD∥BC.
(2)这个命题是真命题,
理由:∵AB∥CD,
∴∠B+∠C=180°,
∵∠A=∠C,
∴∠B+∠A=180°,
∴AD∥BC.
14. (1)解:∵∠A=∠ADE,∴AC∥DE,
∴∠EDC+∠C=180°.
又∵∠EDC=3∠C,∴4∠C=180°,即∠C=45°.
(2)证明:∵AC∥DE,∴∠E=∠ABE.
又∵∠C=∠E,∴∠C=∠ABE,∴BE∥CD.
15. 解:(1)①∠B+∠D=∠BED;②∠B+∠D+∠BED=360°;③∠ABE=∠BED+∠D;④∠B=∠D+∠BED.
(2)选择①.理由如下:
如答图①,过点E作EF∥AB.
∵AB∥CD,∴EF∥CD,
∴∠B=∠BEF,∠D=∠DEF,
∴∠BED=∠BEF+∠DEF=∠B+∠D.
选择②.理由如下:
如答图②,过点E作EF∥AB.
∵AB∥CD,∴EF∥CD,
∴∠B+∠BEF=180°,∠D+∠DEF=180°,
∴∠B+∠BED+∠D=180°+180°=360°.
选择③.理由如下:
如答图③,延长AB交DE于点F.
∵AB∥CD,∴∠D=∠BFE.
∵∠ABE是△BEF的外角,
∴∠ABE=∠BEF+∠BFE=∠BED+∠D.
1
