第二十四章 圆 24.2.1 点和圆的位置关系 课后练习2021-2022学年人教版九年级数学上册(word版 含答案)
文档属性
| 名称 | 第二十四章 圆 24.2.1 点和圆的位置关系 课后练习2021-2022学年人教版九年级数学上册(word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 271.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 14:11:10 | ||
图片预览


文档简介
2021——2022学年度人教版九年级数学上册 第二十四章 圆 24.2.1 点和圆的位置关系 课后练习
一、选择题
1.平面直角坐标系中,⊙O的圆心在原点,半径为5,则点与⊙O的位置关系是( )
A.点在⊙O内 B.点在⊙O上 C.点在⊙O外 D.无法确定
2.如图,在中,,以该三角形的三条边为边向形外作正方形,正方形的顶点都在同一个圆上.记该圆面积为,面积为,则的值是( )
A. B. C. D.
3.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,D是以点A为圆心,4为半径的圆上一点,连接BD,M为BD的中点,则线段CM长度的最大值( )
A.14 B.7 C.9 D.6
4.如图,⊙O是△ABC的外接圆,∠A=62°,E是BC的中点,连接OE并延长交⊙O于点D,连接BD,则∠D的度数为( )
A.58° B.59° C.60° D.61°
5.如图,已知直线与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最小值为( )
A.5.5 B.10.5 C.8 D.12
6.如图,点为的外心,为正三角形,与相交于点,连接.若,,则的度数为( )
A. B. C. D.
7.如图,平面直角坐标系中,点A是y轴正半轴上任意一点,B(-3,0),C(4,0),则当点A在y轴上运动时,△ABC的外心不可能在( )
A.第三象限 B.第一象限 C.第四象限 D.x轴上
8.如图,根据下列尺规作图痕迹,其中表示点O是△ABC外心的是( )
A.B. C. D.
9.引理:在中,若为的中点,则.(中线长公式,不用证明,可以直接应用)根据这个引理,解决下面的问题:如图,在矩形中,,,点在以为直径的半圆上运动,则的最小值是( )
A. B.38 C.40 D.68
10.如图,在已知的△ABC中,按以下步骤:(1)分别以B、C为圆心,大于BC的长为半径作弧,两弧相交M、N;(2)作直线MN,交AB于D,连接CD,若CD=AD,∠B=25°,则下列结论中错误的是( )
A.直线MN是线段BC的垂直平分线
B.点D为△ABC的外心
C.∠ACB=90°
D.点D为△ABC的内心
二、填空题
11.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=8,则S△ABC=___________.
12.一个直角三角形的两条边长是方程的两个根,则此直角三角形的外接圆的直径为________.
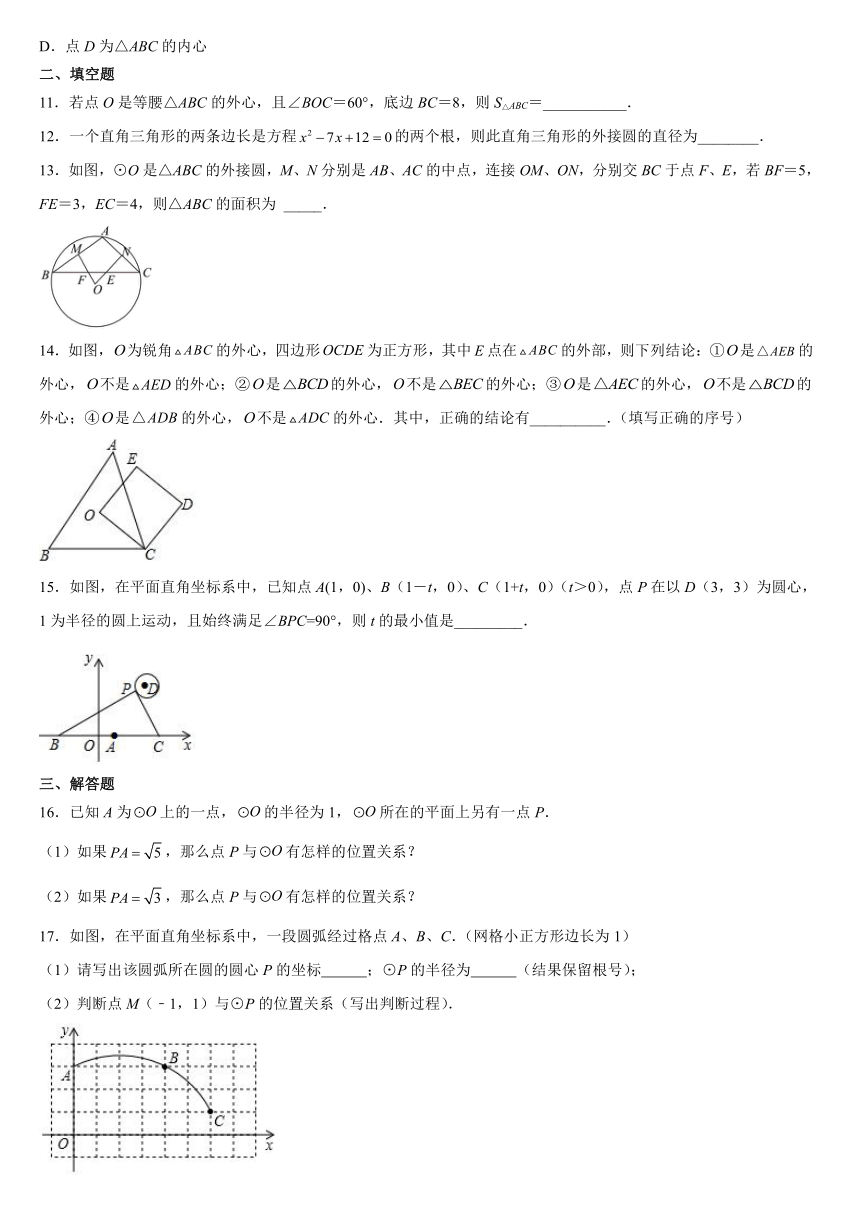
13.如图,⊙O是△ABC的外接圆,M、N分别是AB、AC的中点,连接OM、ON,分别交BC于点F、E,若BF=5,FE=3,EC=4,则△ABC的面积为 _____.
14.如图,为锐角的外心,四边形为正方形,其中点在的外部,则下列结论:①是的外心,不是的外心;②是的外心,不是的外心;③是的外心,不是的外心;④是的外心,不是的外心.其中,正确的结论有__________.(填写正确的序号)
15.如图,在平面直角坐标系中,已知点A(1,0)、B(1-t,0)、C(1+t,0)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是_________.
三、解答题
16.已知A为上的一点,的半径为1,所在的平面上另有一点P.
(1)如果,那么点P与有怎样的位置关系?
(2)如果,那么点P与有怎样的位置关系?
17.如图,在平面直角坐标系中,一段圆弧经过格点A、B、C.(网格小正方形边长为1)
(1)请写出该圆弧所在圆的圆心P的坐标 ;⊙P的半径为 (结果保留根号);
(2)判断点M(﹣1,1)与⊙P的位置关系(写出判断过程).
18.如图,菱形的对角线与交于点E,,的外接圆为.
(1)求的半径;
(2)分别判断点D和点E与的位置关系,并说明理由.
19.如图,已知抛物线与x轴交于A,B两点(A在左边),抛物线经过点,顶点为M.
(1)写出M点的坐标,并指出函数y最值?求a的值.
(2)以AB为直径画,试判定点D与的位置关系,并证明.
20.阅读下列材料,并完成相应的学习任务:
我们知道三角形外接圆的圆心叫做三角形的外心,三角形内切圆的圆心叫做三角形的内心.由于三角形的三条高(或高所在的直线)相交于一点,因此我们把三角形三条高的交点叫做三角形的垂心.下面我们以锐角三角形为例,证明三角形的三条高相交于一点.
如图,在△ABC中,AD,BE分别是BC,AC边上的高,且AD与BE相交于点P.连接CP并延长,交AB于点F.
求证:CF⊥AB.
证明:分别过点A,B,C作它们所对边的平行线,三条平行线两两相交于点M,N,Q.分别连接PM,PN,PQ.
∵MNBC,MQAB,NQAC,
∴四边形MABC,四边形ANBC,四边形ABQC都是平行四边形.
∴BC=AM=AN,AC=BN=BQ,AB=MC=CQ.
∵AD⊥BC,
∴∠MAD=∠ADB=90°,即AD⊥MN.
∴PM=PN.
…
学习任务:
(1)请将上面剩余的证明过程补充完整;
(2)点P是△MNQ的 .(填出字母代号即可)
A.内心 B.外心 C.垂心 D.重心
(3)若∠CAB=40°,则∠MPN= °.
21.如图,抛物线过点,且与直线交于、两点,点的坐标为.
(1)求抛物线的解析式;
(2)点为抛物线上位于直线上方的一点,过点作轴交直线于点,点为对称轴上一动点,当线段的长度最大时,求的最小值;
(3)设点为抛物线的顶点,在轴上是否存在点,使?若存在,求点的坐标;若不存在,请说明理由.
22.锐角外接圆的圆心为O,线段的中点分别为M、N,,.设.
(1)请直接用表示;
(2)判断的形状,并给出证明;
(3)求的大小.
23.如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
(1)求抛物线的解析式及点B坐标;
(2)试探究的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求面积 的最大值,并求出此时M点的坐标.
【参考答案】
1.A 2.A 3.B 4.B 5.A 6.A 7.A 8.C 9.C 10.D
11.32+16或32﹣16
12.4或5或4
13.24
14.①③
15..
16.(1)点P在外;(2)点P可能在外,也可能在内,还可能在上,实际上,点P位于以A为圆心,以为半径的圆上.
17.(1)(2,﹣1),2;(2)圆内
18.(1)5;(2)点E在内,点D在外
19.(1),最小值为,;(2)点D在上
20.(1)略;(2)B;(3)80°
21.(1);(2);(3)存在,点的坐标为、
22.(1)∠BAC=180°-10θ,∠MON=180°-2θ;(2)等腰三角形;(3)12°
23.(1)抛物线解析式为,B点坐标为(3,0);(2)△ABC外接圆圆心在直线上,其坐标为(1,);(3)的最大值为,此时M点的坐标为(,).
一、选择题
1.平面直角坐标系中,⊙O的圆心在原点,半径为5,则点与⊙O的位置关系是( )
A.点在⊙O内 B.点在⊙O上 C.点在⊙O外 D.无法确定
2.如图,在中,,以该三角形的三条边为边向形外作正方形,正方形的顶点都在同一个圆上.记该圆面积为,面积为,则的值是( )
A. B. C. D.
3.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,D是以点A为圆心,4为半径的圆上一点,连接BD,M为BD的中点,则线段CM长度的最大值( )
A.14 B.7 C.9 D.6
4.如图,⊙O是△ABC的外接圆,∠A=62°,E是BC的中点,连接OE并延长交⊙O于点D,连接BD,则∠D的度数为( )
A.58° B.59° C.60° D.61°
5.如图,已知直线与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最小值为( )
A.5.5 B.10.5 C.8 D.12
6.如图,点为的外心,为正三角形,与相交于点,连接.若,,则的度数为( )
A. B. C. D.
7.如图,平面直角坐标系中,点A是y轴正半轴上任意一点,B(-3,0),C(4,0),则当点A在y轴上运动时,△ABC的外心不可能在( )
A.第三象限 B.第一象限 C.第四象限 D.x轴上
8.如图,根据下列尺规作图痕迹,其中表示点O是△ABC外心的是( )
A.B. C. D.
9.引理:在中,若为的中点,则.(中线长公式,不用证明,可以直接应用)根据这个引理,解决下面的问题:如图,在矩形中,,,点在以为直径的半圆上运动,则的最小值是( )
A. B.38 C.40 D.68
10.如图,在已知的△ABC中,按以下步骤:(1)分别以B、C为圆心,大于BC的长为半径作弧,两弧相交M、N;(2)作直线MN,交AB于D,连接CD,若CD=AD,∠B=25°,则下列结论中错误的是( )
A.直线MN是线段BC的垂直平分线
B.点D为△ABC的外心
C.∠ACB=90°
D.点D为△ABC的内心
二、填空题
11.若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=8,则S△ABC=___________.
12.一个直角三角形的两条边长是方程的两个根,则此直角三角形的外接圆的直径为________.
13.如图,⊙O是△ABC的外接圆,M、N分别是AB、AC的中点,连接OM、ON,分别交BC于点F、E,若BF=5,FE=3,EC=4,则△ABC的面积为 _____.
14.如图,为锐角的外心,四边形为正方形,其中点在的外部,则下列结论:①是的外心,不是的外心;②是的外心,不是的外心;③是的外心,不是的外心;④是的外心,不是的外心.其中,正确的结论有__________.(填写正确的序号)
15.如图,在平面直角坐标系中,已知点A(1,0)、B(1-t,0)、C(1+t,0)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是_________.
三、解答题
16.已知A为上的一点,的半径为1,所在的平面上另有一点P.
(1)如果,那么点P与有怎样的位置关系?
(2)如果,那么点P与有怎样的位置关系?
17.如图,在平面直角坐标系中,一段圆弧经过格点A、B、C.(网格小正方形边长为1)
(1)请写出该圆弧所在圆的圆心P的坐标 ;⊙P的半径为 (结果保留根号);
(2)判断点M(﹣1,1)与⊙P的位置关系(写出判断过程).
18.如图,菱形的对角线与交于点E,,的外接圆为.
(1)求的半径;
(2)分别判断点D和点E与的位置关系,并说明理由.
19.如图,已知抛物线与x轴交于A,B两点(A在左边),抛物线经过点,顶点为M.
(1)写出M点的坐标,并指出函数y最值?求a的值.
(2)以AB为直径画,试判定点D与的位置关系,并证明.
20.阅读下列材料,并完成相应的学习任务:
我们知道三角形外接圆的圆心叫做三角形的外心,三角形内切圆的圆心叫做三角形的内心.由于三角形的三条高(或高所在的直线)相交于一点,因此我们把三角形三条高的交点叫做三角形的垂心.下面我们以锐角三角形为例,证明三角形的三条高相交于一点.
如图,在△ABC中,AD,BE分别是BC,AC边上的高,且AD与BE相交于点P.连接CP并延长,交AB于点F.
求证:CF⊥AB.
证明:分别过点A,B,C作它们所对边的平行线,三条平行线两两相交于点M,N,Q.分别连接PM,PN,PQ.
∵MNBC,MQAB,NQAC,
∴四边形MABC,四边形ANBC,四边形ABQC都是平行四边形.
∴BC=AM=AN,AC=BN=BQ,AB=MC=CQ.
∵AD⊥BC,
∴∠MAD=∠ADB=90°,即AD⊥MN.
∴PM=PN.
…
学习任务:
(1)请将上面剩余的证明过程补充完整;
(2)点P是△MNQ的 .(填出字母代号即可)
A.内心 B.外心 C.垂心 D.重心
(3)若∠CAB=40°,则∠MPN= °.
21.如图,抛物线过点,且与直线交于、两点,点的坐标为.
(1)求抛物线的解析式;
(2)点为抛物线上位于直线上方的一点,过点作轴交直线于点,点为对称轴上一动点,当线段的长度最大时,求的最小值;
(3)设点为抛物线的顶点,在轴上是否存在点,使?若存在,求点的坐标;若不存在,请说明理由.
22.锐角外接圆的圆心为O,线段的中点分别为M、N,,.设.
(1)请直接用表示;
(2)判断的形状,并给出证明;
(3)求的大小.
23.如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
(1)求抛物线的解析式及点B坐标;
(2)试探究的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求面积 的最大值,并求出此时M点的坐标.
【参考答案】
1.A 2.A 3.B 4.B 5.A 6.A 7.A 8.C 9.C 10.D
11.32+16或32﹣16
12.4或5或4
13.24
14.①③
15..
16.(1)点P在外;(2)点P可能在外,也可能在内,还可能在上,实际上,点P位于以A为圆心,以为半径的圆上.
17.(1)(2,﹣1),2;(2)圆内
18.(1)5;(2)点E在内,点D在外
19.(1),最小值为,;(2)点D在上
20.(1)略;(2)B;(3)80°
21.(1);(2);(3)存在,点的坐标为、
22.(1)∠BAC=180°-10θ,∠MON=180°-2θ;(2)等腰三角形;(3)12°
23.(1)抛物线解析式为,B点坐标为(3,0);(2)△ABC外接圆圆心在直线上,其坐标为(1,);(3)的最大值为,此时M点的坐标为(,).
同课章节目录
