2021-2022学年北师大版数学八年级上册第五章 二元一次方程组 章节测试 (word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版数学八年级上册第五章 二元一次方程组 章节测试 (word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 377.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 14:56:44 | ||
图片预览




文档简介
第五章 二元一次方程组
一、单选题
1.关于x,y的二元一次方程组的解也是二元一次方程2x+3y=﹣6的解,则k的值是( )
A.﹣ B. C. D.﹣
2.如图,10块形状、大小相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为x厘米和y厘米,则依题意可列方程组为( )
A. B. C. D.
3.已知关于x、y的方程x2m-n-2+ym+n+1=6是二元一次方程,则m,n的值为( )
A.m=1,n=﹣1 B.m=﹣1,n=1
C.m=,n=﹣ D.m=﹣,n=
4.若方程组的解满足,则的值为( )
A. B.1 C.0 D.不能确定
5.下列是二元一次方程的是( )
A. B. C. D.
6.甲、乙两地相距360千米,一轮船往返于甲、乙两地之间,顺水行船用18小时,逆水行船用24小时,若设船在静水中的速度为x千米/时,水流速度为y千米/时,则下列方程组中正确的是( )
A. B. C. D.
7.我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有匹,小马有匹,则可列方程组为( )
A. B.
C. D.
8.甲、乙两人练习跑步.如果乙先跑10米,则甲跑5秒就可追上乙;如果乙先跑2秒,则甲跑4秒就可追上乙.若设甲的速度为米/秒,乙的速度为米/秒,则下列方程组中正确的是( )
A. B. C. D.
9.如果方程 与下面方程中的一个组成的方程组的解为 那么这个方程可以
A. B. C. D.
10.若方程组仅有一组解,则m的取值是( )
A.m可以取任何实数 B.
C. D.以上均不对
11.为了丰富同学们的课余生活,体育委员小强到体育用品商店购买羽毛球拍和乒乓球拍,若购买1副羽毛球拍和1副乒乓球拍共需50元,小强一共用320元购买了6副同样的羽毛球拍和10副同样的乒乓球拍,若设每副羽毛球拍为x元,每副乒乓球拍为y元,列二元一次方程组得( )
A. B. C. D.
12.端午节前夕,某超市用元购进A,B两种商品共,其中A型商品每件元,B型商品每件36元.设购买A型商品件、B型商品件,依题意列方程组正确的是( )
A. B.
C. D.
13.等腰三角形的周长是40 cm,腰长y(cm)是底边长x(cm)的函数.此函数的表达式和自变量取值范围正确的是( )
A.y=-2x+40(0<x<20) B.y=-0.5x+20(10<x<20)
C.y=-2x+40(10<x<20) D.y=-0.5x+20(0<x<20)
14.已知是二元一次方程组的解,则的值为
A.-1 B.1 C.2 D.3
15.方程组没有解,因此直线y=﹣x+2和直线y=﹣x+在同一平面直角坐标系中的位置关系是( )
A.重合 B.平行 C.相交 D.以上三种情况都有可能
二、填空题
16.已知二元一次方程组,则x﹣y=_____,x+y=_____.
17.已知和都是ax+by=7的解,则a=____,b=_____.
18.由一次函数与的图象与x轴围成的三角形面积是________.
19.如果是二元一次方程,那么的值是________.
20.若一个二元一次方程的一个解为,则这个方程可能是________.(填出符合条件的一个即可)
21.某班共有学生49人,该班某男生因事请假,当天的男生人数恰为女生人数的一半.若设该班男生人数为x,女生人数为y,列出关于x,y的方程组为________________.
三、解答题
22.解方程组:(1);(2);(3);(4).
23.在代数式中,当,2,3时,代数式的值依次是0,3,28.
(1)求a,b,c的值;
(2)当时,求这个代数式的值.
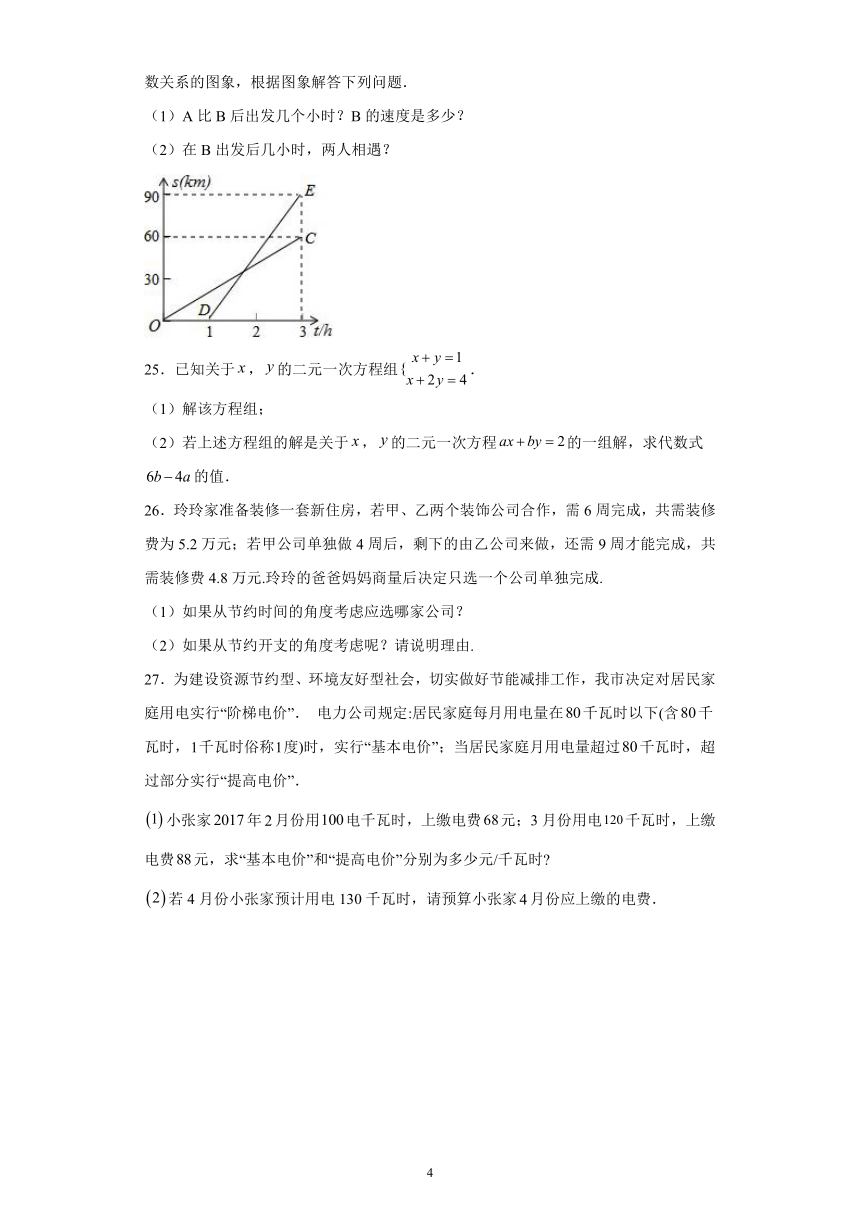
24.已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
25.已知关于,的二元一次方程组.
(1)解该方程组;
(2)若上述方程组的解是关于,的二元一次方程的一组解,求代数式的值.
26.玲玲家准备装修一套新住房,若甲、乙两个装饰公司合作,需6周完成,共需装修费为5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成,共需装修费4.8万元.玲玲的爸爸妈妈商量后决定只选一个公司单独完成.
(1)如果从节约时间的角度考虑应选哪家公司?
(2)如果从节约开支的角度考虑呢?请说明理由.
27.为建设资源节约型、环境友好型社会,切实做好节能减排工作,我市决定对居民家庭用电实行“阶梯电价”. 电力公司规定:居民家庭每月用电量在千瓦时以下(含千瓦时,千瓦时俗称度)时,实行“基本电价”;当居民家庭月用电量超过千瓦时,超过部分实行“提高电价”.
小张家年月份用电千瓦时,上缴电费元;3月份用电千瓦时,上缴电费元,求“基本电价”和“提高电价”分别为多少元/千瓦时
若4月份小张家预计用电130千瓦时,请预算小张家月份应上缴的电费.
参考答案
1.A
解:解方程组 ,
得:x=7k,y=﹣2k,
把x,y代入二元一次方程2x+3y=﹣6,
得:2×7k+3×(﹣2k)=﹣6,
解得:k=﹣,
故选:A.
2.B
解:由题图可得等量关系式:
故选B.
3.A
∵关于x、y的方程x2m﹣n﹣2+ym+n+1=6是二元一次方程,
∴,
解得.
故选:A.
4.B
解:①+②,得
3(x+y)=3-3k,
由x+y=0,得
3-3k=0,
解得k=1,
故选:B.
5.B
A、是一元一次方程,此项不符题意;
B、是二元一次方程,此项符合题意;
C、是分式方程,此项不符题意;
D、是二元二次方程,此项不符题意;
故选:B.
6.A
根据题意可得,顺水速度为:,逆水速度为:,所以根据所走的路程可列方程组为,故选A.
7.B
解:设大马有匹,小马有匹,由题意得:
,
故选:B.
8.A
设甲的速度为米/秒,乙的速度为米/秒,根据题意得:
故选:A
9.D
解:A、由,解得:,故本项错误;
B、由,解得:,故本项错误;
C、由,解得:,故本项错误;
D、,解得:,故本项正确;
故选择:D.
10.C
,
①×2-②×3得,
(8+9m)y=0,
当8+9m≠0时,方程有一个解,
即时,方程有一个解,
故选C.
11.B
设每副羽毛球拍为x元,每副乒乓球拍为y元,由题意得,
故选B.
12.B
解:设购买A型商品x件、B型商品y件,依题意列方程组:
.
故选B..
13.D
解:根据三角形周长等于三边之和可得:2y=40-x
∴y=-0.5x+20,
根据三角形三边关系可得:x<2y,x>y-y
∴可知0<x<20
故选D.
14.A
∵已知是二元一次方程组的解,
∴
由①+②,得a=2,
由①-②,得b=3,
∴a-b=-1;
故选A.
考点:二元一次方程的解.
15.B
方程组可化为,若方程组没有解,说明直线y=﹣x+2和直线y=﹣x+在同一平面直角坐标系中没有交点,所以,两条直线平行.
故选B
16.-1 5
解:
①-②得x﹣y=-1
①+②得3(x+y)=15,则x+y=5
故答案为:-1,5
17.2 1
解决此题可将两组x,y的值代入方程,列出方程组,即可解出a,b的值.
解答:把和代入方程,
得
解这个方程组,得
“点睛”本题既考查了二元一次方程的概念又考查了二元一次方程组的解法.
18.1
如图所示一次函数y=x+1与y= x 3的图象与x轴围成三角形为ABC,
当y= x 3的图象与x轴相交时得到A(-3,0),
当函数y=x+1的图象与x轴相交时得到B(-1,0),
∴AB=2,
∵一次函数y=x+1与y= x 3的交点C坐标为( 2, 1),
∴三角形ABC的高为1,
∴三角形ABC的面积为:×2×1=1,
故答案为:1.
19.2
由是二元一次方程,得
,
解得 .
=1+1=2.
故答案为:2.
20.答案不唯一,如
这个方程可能是:,答案不唯一.
故答案是:,答案不唯一.
21.
解:根据该班一男生请假后,男生人数恰为女生人数的一半,得x 1=y,即y=2(x 1);根据该班共有学生49人,得x+y=49.
所以列方程组为:,
故答案为:.
22.(1);(2);(3);(4);
(1)①+②得,4x=8,
解得,x=2,
把x=2代入①得,y=1,
即方程组的解为 ;
(2)①×2+②,得7x=-7,
解,得x=-1
把x=-1代入①,得y=3,
即方程组的解为;
(3)①×4+②×3得,8x+9x=28+6,
解得x=2
把x=2代入②得y=1,
即方程组的解为 ;
(4)原方程组整理得
①+②得6x=18,
解得x=3,
②-①得4y=2,
解得y=,
即方程组的解为 ;
23.(1),,;(2)60.
解:(1)由题意可得,将,2,3分别代入代数式得:
由①得:④
将④代入②得:⑤,
将④代入③得:⑥,
⑥-⑤得:
将代入⑤得:
将、代入①式得:,解得
故答案为:,,
(2)由(1)得,此代数式为
将代入得:
故答案为
24.(1)1,20 km/h;(2).
解:(1)由图可知,A比B后出发1小时;
B的速度:60÷3=20(km/h);
(2)由图可知点D(1,0),C(3,60),E(3,90),
设OC的解析式为s=kt,
则3k=60,
解得k=20,
所以,s=20t,
设DE的解析式为s=mt+n,
则 ,
解得,
所以,s=45t﹣45,
由题意得,
解得,
所以,B出发小时后两人相遇.
25.(1) ;(2)4
(1) 得出;
(2)-2a+3b=2则=4
26.(1)甲公司;(2)乙公司.
(1)设甲公司的每周工作效率为m,乙公司每周的工作效率为n ,由题意得:
, 解得,
甲公司单独完成需要1÷=10周,
乙公司单独完成需要1÷=15周,
故从节约时间的角度考虑应选择甲公司;
(2)由(1)知甲、乙完成这次工程分别需10周、15周 ,
设需付甲公司每周装修费x万元,乙公司y万元,
则,解得,
所以甲公司单独完成需要装修费10×=6万元,
乙公司单独完成需要装修费15×=4万元,
故从节约开支的角度出发应选择乙公司 .
27.(1)基本电价为0.6元/千瓦时,提高电价为1元/千瓦时;(2)98元
(1)设“基本电价”为元/千瓦时,“提高电价”为元/千瓦时
由题意有,
解得:,
答:“基本电价”为0.6元/千瓦时,“提高电价”为1元/千瓦时.
(2)4月份应上缴电费:(元)
答:预计小张家4月份上缴的电费为98元.
一、单选题
1.关于x,y的二元一次方程组的解也是二元一次方程2x+3y=﹣6的解,则k的值是( )
A.﹣ B. C. D.﹣
2.如图,10块形状、大小相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为x厘米和y厘米,则依题意可列方程组为( )
A. B. C. D.
3.已知关于x、y的方程x2m-n-2+ym+n+1=6是二元一次方程,则m,n的值为( )
A.m=1,n=﹣1 B.m=﹣1,n=1
C.m=,n=﹣ D.m=﹣,n=
4.若方程组的解满足,则的值为( )
A. B.1 C.0 D.不能确定
5.下列是二元一次方程的是( )
A. B. C. D.
6.甲、乙两地相距360千米,一轮船往返于甲、乙两地之间,顺水行船用18小时,逆水行船用24小时,若设船在静水中的速度为x千米/时,水流速度为y千米/时,则下列方程组中正确的是( )
A. B. C. D.
7.我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有匹,小马有匹,则可列方程组为( )
A. B.
C. D.
8.甲、乙两人练习跑步.如果乙先跑10米,则甲跑5秒就可追上乙;如果乙先跑2秒,则甲跑4秒就可追上乙.若设甲的速度为米/秒,乙的速度为米/秒,则下列方程组中正确的是( )
A. B. C. D.
9.如果方程 与下面方程中的一个组成的方程组的解为 那么这个方程可以
A. B. C. D.
10.若方程组仅有一组解,则m的取值是( )
A.m可以取任何实数 B.
C. D.以上均不对
11.为了丰富同学们的课余生活,体育委员小强到体育用品商店购买羽毛球拍和乒乓球拍,若购买1副羽毛球拍和1副乒乓球拍共需50元,小强一共用320元购买了6副同样的羽毛球拍和10副同样的乒乓球拍,若设每副羽毛球拍为x元,每副乒乓球拍为y元,列二元一次方程组得( )
A. B. C. D.
12.端午节前夕,某超市用元购进A,B两种商品共,其中A型商品每件元,B型商品每件36元.设购买A型商品件、B型商品件,依题意列方程组正确的是( )
A. B.
C. D.
13.等腰三角形的周长是40 cm,腰长y(cm)是底边长x(cm)的函数.此函数的表达式和自变量取值范围正确的是( )
A.y=-2x+40(0<x<20) B.y=-0.5x+20(10<x<20)
C.y=-2x+40(10<x<20) D.y=-0.5x+20(0<x<20)
14.已知是二元一次方程组的解,则的值为
A.-1 B.1 C.2 D.3
15.方程组没有解,因此直线y=﹣x+2和直线y=﹣x+在同一平面直角坐标系中的位置关系是( )
A.重合 B.平行 C.相交 D.以上三种情况都有可能
二、填空题
16.已知二元一次方程组,则x﹣y=_____,x+y=_____.
17.已知和都是ax+by=7的解,则a=____,b=_____.
18.由一次函数与的图象与x轴围成的三角形面积是________.
19.如果是二元一次方程,那么的值是________.
20.若一个二元一次方程的一个解为,则这个方程可能是________.(填出符合条件的一个即可)
21.某班共有学生49人,该班某男生因事请假,当天的男生人数恰为女生人数的一半.若设该班男生人数为x,女生人数为y,列出关于x,y的方程组为________________.
三、解答题
22.解方程组:(1);(2);(3);(4).
23.在代数式中,当,2,3时,代数式的值依次是0,3,28.
(1)求a,b,c的值;
(2)当时,求这个代数式的值.
24.已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
25.已知关于,的二元一次方程组.
(1)解该方程组;
(2)若上述方程组的解是关于,的二元一次方程的一组解,求代数式的值.
26.玲玲家准备装修一套新住房,若甲、乙两个装饰公司合作,需6周完成,共需装修费为5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成,共需装修费4.8万元.玲玲的爸爸妈妈商量后决定只选一个公司单独完成.
(1)如果从节约时间的角度考虑应选哪家公司?
(2)如果从节约开支的角度考虑呢?请说明理由.
27.为建设资源节约型、环境友好型社会,切实做好节能减排工作,我市决定对居民家庭用电实行“阶梯电价”. 电力公司规定:居民家庭每月用电量在千瓦时以下(含千瓦时,千瓦时俗称度)时,实行“基本电价”;当居民家庭月用电量超过千瓦时,超过部分实行“提高电价”.
小张家年月份用电千瓦时,上缴电费元;3月份用电千瓦时,上缴电费元,求“基本电价”和“提高电价”分别为多少元/千瓦时
若4月份小张家预计用电130千瓦时,请预算小张家月份应上缴的电费.
参考答案
1.A
解:解方程组 ,
得:x=7k,y=﹣2k,
把x,y代入二元一次方程2x+3y=﹣6,
得:2×7k+3×(﹣2k)=﹣6,
解得:k=﹣,
故选:A.
2.B
解:由题图可得等量关系式:
故选B.
3.A
∵关于x、y的方程x2m﹣n﹣2+ym+n+1=6是二元一次方程,
∴,
解得.
故选:A.
4.B
解:①+②,得
3(x+y)=3-3k,
由x+y=0,得
3-3k=0,
解得k=1,
故选:B.
5.B
A、是一元一次方程,此项不符题意;
B、是二元一次方程,此项符合题意;
C、是分式方程,此项不符题意;
D、是二元二次方程,此项不符题意;
故选:B.
6.A
根据题意可得,顺水速度为:,逆水速度为:,所以根据所走的路程可列方程组为,故选A.
7.B
解:设大马有匹,小马有匹,由题意得:
,
故选:B.
8.A
设甲的速度为米/秒,乙的速度为米/秒,根据题意得:
故选:A
9.D
解:A、由,解得:,故本项错误;
B、由,解得:,故本项错误;
C、由,解得:,故本项错误;
D、,解得:,故本项正确;
故选择:D.
10.C
,
①×2-②×3得,
(8+9m)y=0,
当8+9m≠0时,方程有一个解,
即时,方程有一个解,
故选C.
11.B
设每副羽毛球拍为x元,每副乒乓球拍为y元,由题意得,
故选B.
12.B
解:设购买A型商品x件、B型商品y件,依题意列方程组:
.
故选B..
13.D
解:根据三角形周长等于三边之和可得:2y=40-x
∴y=-0.5x+20,
根据三角形三边关系可得:x<2y,x>y-y
∴可知0<x<20
故选D.
14.A
∵已知是二元一次方程组的解,
∴
由①+②,得a=2,
由①-②,得b=3,
∴a-b=-1;
故选A.
考点:二元一次方程的解.
15.B
方程组可化为,若方程组没有解,说明直线y=﹣x+2和直线y=﹣x+在同一平面直角坐标系中没有交点,所以,两条直线平行.
故选B
16.-1 5
解:
①-②得x﹣y=-1
①+②得3(x+y)=15,则x+y=5
故答案为:-1,5
17.2 1
解决此题可将两组x,y的值代入方程,列出方程组,即可解出a,b的值.
解答:把和代入方程,
得
解这个方程组,得
“点睛”本题既考查了二元一次方程的概念又考查了二元一次方程组的解法.
18.1
如图所示一次函数y=x+1与y= x 3的图象与x轴围成三角形为ABC,
当y= x 3的图象与x轴相交时得到A(-3,0),
当函数y=x+1的图象与x轴相交时得到B(-1,0),
∴AB=2,
∵一次函数y=x+1与y= x 3的交点C坐标为( 2, 1),
∴三角形ABC的高为1,
∴三角形ABC的面积为:×2×1=1,
故答案为:1.
19.2
由是二元一次方程,得
,
解得 .
=1+1=2.
故答案为:2.
20.答案不唯一,如
这个方程可能是:,答案不唯一.
故答案是:,答案不唯一.
21.
解:根据该班一男生请假后,男生人数恰为女生人数的一半,得x 1=y,即y=2(x 1);根据该班共有学生49人,得x+y=49.
所以列方程组为:,
故答案为:.
22.(1);(2);(3);(4);
(1)①+②得,4x=8,
解得,x=2,
把x=2代入①得,y=1,
即方程组的解为 ;
(2)①×2+②,得7x=-7,
解,得x=-1
把x=-1代入①,得y=3,
即方程组的解为;
(3)①×4+②×3得,8x+9x=28+6,
解得x=2
把x=2代入②得y=1,
即方程组的解为 ;
(4)原方程组整理得
①+②得6x=18,
解得x=3,
②-①得4y=2,
解得y=,
即方程组的解为 ;
23.(1),,;(2)60.
解:(1)由题意可得,将,2,3分别代入代数式得:
由①得:④
将④代入②得:⑤,
将④代入③得:⑥,
⑥-⑤得:
将代入⑤得:
将、代入①式得:,解得
故答案为:,,
(2)由(1)得,此代数式为
将代入得:
故答案为
24.(1)1,20 km/h;(2).
解:(1)由图可知,A比B后出发1小时;
B的速度:60÷3=20(km/h);
(2)由图可知点D(1,0),C(3,60),E(3,90),
设OC的解析式为s=kt,
则3k=60,
解得k=20,
所以,s=20t,
设DE的解析式为s=mt+n,
则 ,
解得,
所以,s=45t﹣45,
由题意得,
解得,
所以,B出发小时后两人相遇.
25.(1) ;(2)4
(1) 得出;
(2)-2a+3b=2则=4
26.(1)甲公司;(2)乙公司.
(1)设甲公司的每周工作效率为m,乙公司每周的工作效率为n ,由题意得:
, 解得,
甲公司单独完成需要1÷=10周,
乙公司单独完成需要1÷=15周,
故从节约时间的角度考虑应选择甲公司;
(2)由(1)知甲、乙完成这次工程分别需10周、15周 ,
设需付甲公司每周装修费x万元,乙公司y万元,
则,解得,
所以甲公司单独完成需要装修费10×=6万元,
乙公司单独完成需要装修费15×=4万元,
故从节约开支的角度出发应选择乙公司 .
27.(1)基本电价为0.6元/千瓦时,提高电价为1元/千瓦时;(2)98元
(1)设“基本电价”为元/千瓦时,“提高电价”为元/千瓦时
由题意有,
解得:,
答:“基本电价”为0.6元/千瓦时,“提高电价”为1元/千瓦时.
(2)4月份应上缴电费:(元)
答:预计小张家4月份上缴的电费为98元.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
