2021-2022学年湘教版九年级数学下册期末综合复习训练 第1章二次函数 (Word版含解析)
文档属性
| 名称 | 2021-2022学年湘教版九年级数学下册期末综合复习训练 第1章二次函数 (Word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 501.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 00:00:00 | ||
图片预览




文档简介
2021-2022学年湘教版九年级数学下册《第1章二次函数》期末综合复习训练1(附答案)
1.下列函数关系中,是二次函数的是( )
A.在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
B.当距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长C与边长a之间的关系
D.半圆面积S与半径R之间的关系
2.在同一平面直角坐标系中,函数y=2x2+kx与y=kx+k(k≠0)的图象大致是( )
A. B. C. D.
3.如图,在4×4的网格中,每一个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点,以O为坐标原点建立如图所示的平面直角坐标系.若抛物线y=x2+bx+c的图象至少经过图中(4×4的网格中)的三个格点,并且至少一个格点在x轴上,则符合要求的抛物线一定不经过的格点坐标为( )
A.(1,3) B.(2,3) C.(1,4) D.(2,4)
4.若函数y=ax2﹣2x+a的图象与坐标轴只有1个交点,则a的取值范围是( )
A.a≥1 B.a>1或a=0
C.a≥1或a=0 D.a>1或a=0或a<﹣1
5.已知抛物线y=ax2+bx+c(a<0)过A(﹣2,0)、B(0,0)、C(﹣3,y1)、D(2,y2)四点,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
6.如图,点A(m,5),B(n,2)是抛物线C1:y=x2﹣2x+3上的两点,将抛物线C1向左平移,得到抛物线C2,点A,B的对应点分别为点A',B'.若曲线段AB扫过的面积为9(图中的阴影部分),则抛物线C2的解析式是( )
A.y=(x﹣5)2+1 B.y=(x﹣2)2+4
C.y=(x+1)2+1 D.y=(x+2)2﹣2
7.若min{a,b,c}表示a,b,c三个数中的最小值,当y=min{x2,x+2,8﹣x}(x≥0)时,则y的最大值是( )
A.4 B.5 C.6 D.7
8.已知函数y=kx2﹣(k+2)x+2(k是常数),下列说法:①函数图象必过第一、二象限; ②当函数图象与坐标轴只有两个交点时,k=0;③当k<﹣2时,抛物线顶点在第一象限;④若k>0,则当x<时,y随着x的增大而减小,其中正确的有( )
A.①②③ B.①③④ C.②④ D.①③
9.已知抛物线y=ax2+3x+c(a,c为常数,且a≠0)经过点(﹣1,﹣1),(0,3),有下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小;③3是方程ax2+2x+c=0的一个根;④当﹣1<x<3时,ax2+2x+c>0其中正确结论的个数是( )
A.1 B.2 C.3 D.4
10.如图,抛物线y=x+2交x轴于点A,B,交y轴于点C,当△ABC纸片上的点C沿着此抛物线运动时,则△ABC纸片随之也跟着移动,设纸片上BC的中点M坐标为(m,n),在此运动过程中,n与m的关系式是( )
A.n=(m﹣)2﹣ B.n=(m﹣)2
C.n=(m﹣)2﹣ D.n=(m﹣)2﹣
11.有一个矩形苗圃园,其中一边靠墙,另外边用长为20m的篱笆围成.已知墙长为15m,若平行于墙的一边长不小于8m,则这个苗圃园面积的最大值和最小值分别为( )
A.48m2,37.5m2 B.50m2,32m2
C.50m2,37.5m2 D.48m2,32m2
12.如图,抛物线y=ax2﹣x+4与直线y=x+b经过点A(2,0),且相交于另一点B;抛物线与y轴交于点C,与x轴交于另一点E;点N在线段AB上,过点N的直线交抛物线于点M,且MN∥y轴,连接AM、BM、BC、AC;当点N在线段AB上移动时(不与A、B重合),下列结论中正确的是( )
A.MN+BN<AB
B.∠BAC=∠BAE
C.∠ACB﹣∠ANM=∠ABC
D.四边形ACBM的最大面积为13
13.已知抛物线y=a(x﹣3)2+过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:
①抛物线的对称轴是直线x=3;
②点C在⊙D外;
③在抛物线上存在一点E,能使四边形ADEC为平行四边形;
④直线CM与⊙D相切.
正确的结论是( )
A.①③ B.①④ C.①③④ D.①②③④
14.二次函数y1=mx2、y2=nx2的图象如图所示,则m n(填“>”或“<”).
15.如果点A(﹣1,4)、B(m,4)在抛物线y=a(x﹣1)2+h上,那么m的值为 .
16.将抛物线y=x2+2x向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的表达式为 ;
17.如图,四边形的两条对角线AC、BD所成的锐角为45°,当AC+BD=12时,四边形ABCD的面积最大值是 .
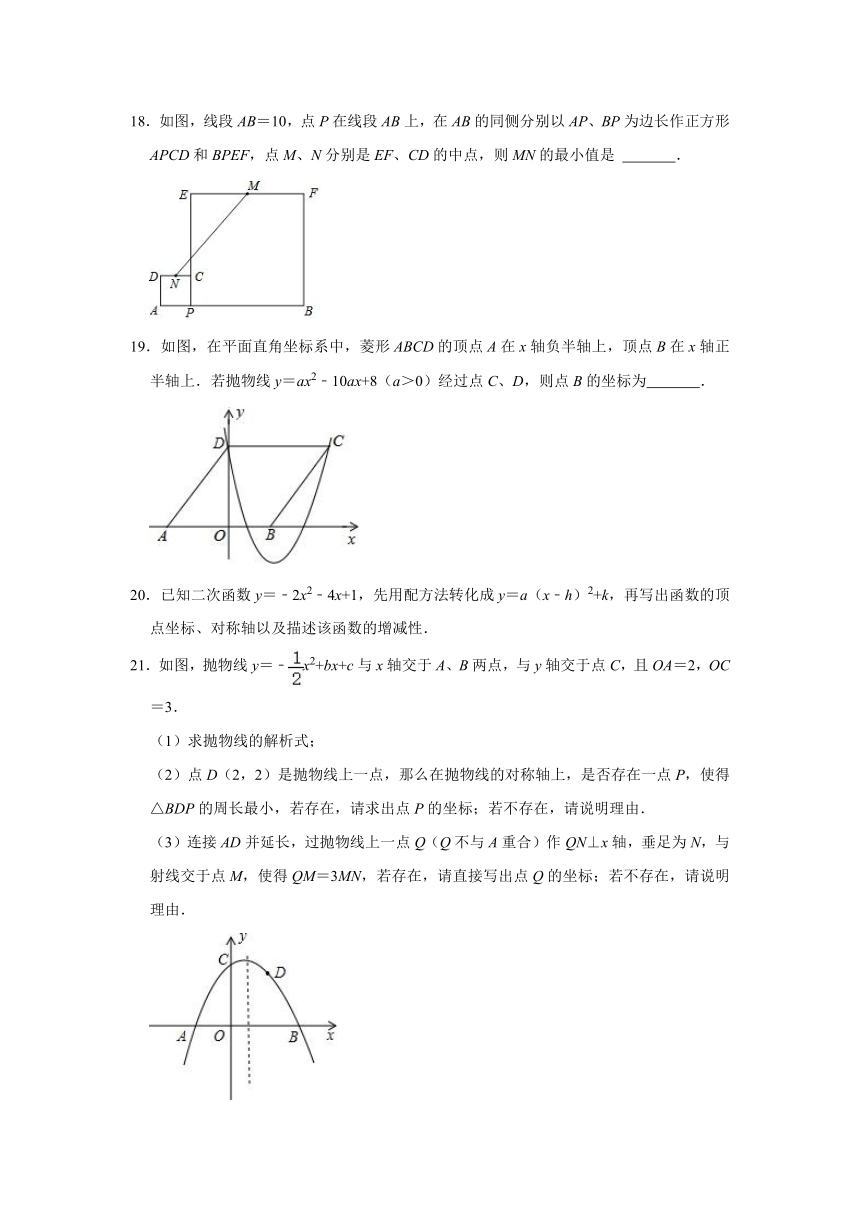
18.如图,线段AB=10,点P在线段AB上,在AB的同侧分别以AP、BP为边长作正方形APCD和BPEF,点M、N分别是EF、CD的中点,则MN的最小值是 .
19.如图,在平面直角坐标系中,菱形ABCD的顶点A在x轴负半轴上,顶点B在x轴正半轴上.若抛物线y=ax2﹣10ax+8(a>0)经过点C、D,则点B的坐标为 .
20.已知二次函数y=﹣2x2﹣4x+1,先用配方法转化成y=a(x﹣h)2+k,再写出函数的顶点坐标、对称轴以及描述该函数的增减性.
21.如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式;
(2)点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
(3)连接AD并延长,过抛物线上一点Q(Q不与A重合)作QN⊥x轴,垂足为N,与射线交于点M,使得QM=3MN,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
22.如图,已知抛物线y=ax2+2x+c与y轴交于点A(0,6),与x轴交于点B(6,0),点P是线段AB上方抛物线上的一个动点.
(1)求这条抛物线的表达式及其顶点坐标;
(2)点M在抛物线上,点N在x轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标:若不存在,请说明理由;
(3)当点P从A点出发沿线段AB上方的抛物线向终点B移动时,点P到直线AB的距离为d,求d最大时点P的坐标.
23.综合与探究:
如图,二次函数y=ax2+bx﹣6的图象与x轴交于A,B两点,并经过点C(8,﹣6),对称轴交x轴于点D.已知点A坐标是(2,0).
(1)求点B和点D的坐标;
(2)连接并延长CD交抛物线于点E,连接BC,BE,求△EBC的面积;
(3)抛物线上有一个动点P,与A,B两点构成△ABP,是否存在S△ABP=S△DBC?若存在,请求出点P的坐标;若不存在,请说明理由.
24.已知抛物线y=ax2+bx+3与x轴交于A(﹣1,0)、B(3,0)两点.
(1)求抛物线解析式;
(2)抛物线与y轴交于点C,在抛物线上存在点P,使S△BAP=S△CAP,求P点坐标;
(3)已知直线l:y=2x﹣1,将抛物线沿y=2x﹣1方向平移,平移过程中与l相交于E、F两点.设平移过程中抛物线的顶点的横坐标为m,在x轴上存在一点P,使∠EPF=90°,求m的范围.
25.如图,抛物线y=ax2+bx+6与x轴交于点A(6,0),B(﹣1,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)若点M为该抛物线对称轴上一点,当CM+BM最小时,求点M的坐标.
(3)抛物线上是否存在点P,使△ACP为直角三角形?若存在,有几个?写出所有符合条件的点P的坐标;若不存在,说明理由.
26.已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=2x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=2x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
参考答案
1.解:A、y=kx+b,是一次函数,错误;
B、t=,是反比例函数,错误;
C、C=3a,是正比例函数,错误;
D、S=.是二次函数,正确;
故选:D.
2.解:当k>0时,函数y=kx+k的图象经过一、二、三象限;函数y=2x2+kx的开口向上,对称轴在y轴的左侧;
当k<0时,函数y=kx+k的图象经过二、三、四象限;函数y=2x2+kx的开口向上,对称轴在y轴的右侧,故C正确.
故选:C.
3.解:∵二次项系数为1,∴该抛物线开口向上
∵图象至少经过图中(4×4的网格中)的三个格点,且至少一个格点在x轴上,
∴结合二次函数的对称性分析如下:
选项A:若过(1,3),将点A坐标代入抛物线表达式并解得:
抛物线的表达式为:y=x2+bx+(2﹣b),
设抛物线过点(2,0),即当x=2时,y=4+2b+2﹣b=0,解得:b=﹣6,
抛物线的表达式为:y=x2﹣6x+8=(x﹣2)(x﹣4),
即抛物线还过点(2,0)、(4,0),不符合题意;
选项B:若过(2,3),还可过点(3,1),将这个点的坐标代入y=x2+bx+c并解得:y=x2﹣7x+13,
若同时过x轴上的可能的格点(4,0),当x=4时,y=1,故B符合题意;
故选:B.
4.解:当a=0时,y=﹣2x,该函数与坐标轴有1个交点;
当a≠0时,△=4﹣4a2<0时,图象与坐标轴只有1个交点,解得:a>1或a<﹣1;
故选:D.
5.解:抛物线y=ax2+bx+c(a<0)过A(﹣2,0)、B(0,0),
则函数的对称轴为:x=﹣1,
x=﹣3比x=2离对称轴近,故y1>y2,
故选:C.
6.解:y=x2﹣2x+3=(x﹣2)2+1.
∵曲线段AB扫过的面积为9(图中的阴影部分),点A(m,5),B(n,2)
∴3BB′=9,
∴BB′=3,
即将函数y=(x﹣2)2+1的图象沿x轴向左平移3个单位长度得到一条新函数的图象,
∴新图象的函数表达式是y=(x+1)2+1.
故选:C.
7.解:解方程x2=x+2得:x=2或x=﹣1,(因为x≥0,x=﹣1舍去),
解方程x+2=8﹣x得:x=3,
解方程x2=8﹣x得:x=,(因为x≥0,x=舍去),
当0≤x≤2时,y的最大值是点A的纵坐标;
当2<x≤时,y的最大值是点B的纵坐标;
当x>时,y的最大值是点C的纵坐标;
如图所示:
y最大=3+2=5,
即y的最大值是5,
故选:B.
8.解:①当k=0时,函数为y=﹣x+2,函数图象经过第一、二、四象限;当k≠0时,△=(k+2)2﹣8k=(k﹣2)2≥0;
k>0时,抛物线开口向上,并且与x轴有交点,函数图象必过第一二象限;k<0时,抛物线开口向下,与y轴相交于y轴正半轴,函数图象必过第一二象限;所以函数图象必经过第一、二象限,故符合题意;
②当k=0时,此函数是不平行于坐标轴的直线,所以,函数与坐标轴有两个交点,当k≠0时,函数是抛物线,必与y轴相交,△=(k+2)2﹣8k=(k﹣2)2≥0,抛物线与x轴有一个(k=2时)或两个交点,此时函数与坐标轴有两个到三个交点,故不符合题意;
③当k<﹣2时,对称轴x=>0,顶点纵坐标==﹣>0,故抛物线顶点在第一象限,符合题意;
④若k>0,抛物线的对称轴为:x=﹣=,则当x<时,y随着x的增大而减小,符合题意;
故选:B.
9.解:把点(﹣1,﹣1),(0,3)代入y=ax2+3x+c得:
∴
∴y=﹣x2+3x+3
∴①ac<0正确;
该抛物线的对称轴为:,
∴②当x>1时,y的值随x值的增大而减小是错误的;
方程ax2+2x+c=0可化为:方程ax2+3x+c=x,
把x=3代入y=﹣x2+3x+3得y=3,
∴﹣x2+2x+3=0,
故③正确;
∴(3,3)在该抛物线上,
又∵抛物线y=ax2+3x+c(a,c为常数,且a≠0)经过点(﹣1,﹣1),
∴抛物线y=ax2+3x+c与y=x的交点为(﹣1,﹣1)和(3,3),
当﹣1<x<3时,ax2+3x+c>x,即ax2+2x+c>0
④当﹣1<x<3时,ax2+2x+c>0,故④正确.
综上,①③④正确.
故选:C.
10.解:∵抛物线y=x+2交x轴于点A,B,交y轴于点C,
∴点B的坐标为(4,0),点C的坐标为(0,2),
∴BC的中点M坐标为(,),即点M坐标为(2,1).
∵点C沿着此抛物线运动,点M也随之运动,点M的运动轨迹是抛物线,且经过(2,1),(6,﹣1)
∴设抛物线的解析式为y=x2+bx+c,
则有,解得
∴m,n满足,n=m2﹣m+8=(m﹣)2﹣,
故选:D.
11.解:设平行于墙的一边长为xm,苗圃园面积为Sm2,则
S=x×(20﹣x)
=﹣(x2﹣20x)
=﹣(x﹣10)2+50 (8≤x≤15)
∵﹣<0
∴S有最大值,x=10>8时,S最大=50
∵墙长为15m
∴当x=15时,S最小
S最小=15××(20﹣15)=37.5
∴这个苗圃园面积的最大值和最小值分别为50m2,37.5m2.
故选:C.
12.解:将点A(2,0)代入抛物线y=ax2﹣x+4与直线y=x+b
解得:a=,b=﹣,
设:M点横坐标为m,则M(m,m2﹣m+4)、N(m,m﹣),
其它点坐标为A(2,0)、B(5,4)、C(0,4),
则AB=BC=5,则∠CAB=∠ACB,
∴△ABC是等腰三角形.
A、当MN过对称轴的直线时,此时点M、N的坐标分别为(,﹣)、(,),
由勾股定理得:BN=,而MN=,
BN+MN=5=AB,
故本选项错误;
B、∵BC∥x轴(B、C两点y坐标相同),
∴∠BAE=∠CBA,而△ABC是等腰三角形不是等边三角形,
∠CBA≠∠BCA,
∴∠BAC=∠BAE不成立,
故本选项错误;
C、如上图,过点A作AD⊥BC、BF⊥AC,
∵△ABC是等腰三角形,
∴BF是∠ABC的平分线,
易证:∠CAD=∠ABF=ABC,
而∠ACB﹣∠ANM=∠CAD=ABC,
故本选项正确;
D、S四边形ACBM=S△ABC+S△ABM,
S△ABC=10,
S△ABM=MN (xB﹣xA)=﹣m2+7m﹣10,其最大值为,
故S四边形ACBM的最大值为10+=12.25,
故本选项错误.
故选:C.
13.解:由抛物线y=a(x﹣3)2+可知:抛物线的对称轴x=3,故①正确;
∵抛物线y=a(x﹣3)2+过点C(0,4),
∴4=9a+,解得:a=﹣,
∴抛物线的解析式为y=﹣(x﹣3)2+,
令y=0,则﹣(x﹣3)2+=0,解得:x=8或x=﹣2,
∴A(﹣2,0),B(8,0);
∴AB=10,
∴AD=5,
∴OD=3
∵C(0,4),
∴CD==5,
∴CD=AD,
∴点C在圆上,故②错误;
过点C作CE∥AB,交抛物线于E,
∵C(0,4),
代入y=﹣(x﹣3)2+得:4=﹣(x﹣3)2+,
解得:x=0或x=6,
∴CE=6,
∴AD≠CE,
∴四边形ADEC不是平行四边形,故③错误;
由抛物线y=a(x﹣3)2+可知:M(3,),
∵C(0,4),
∴直线CM为y=x+4,直线CD为:y=﹣x+4,
∴CM⊥CD,
∵CD=AD=5,
∴直线CM与⊙D相切,故④正确;
故选:B.
14.解:根据抛物线的开口大小与二次函数的二次项系数的关系:系数越大,开口越小,
故m>n,
故答案为>.
15.解:由点A(﹣1,4)、B(m,4)在抛物线y=a(x﹣1)2+h上,得
(﹣1,4)与(m,4)关于对称轴x=1对称,
m﹣1=1﹣(﹣1),
解得m=3,
故答案为:3.
16.解:y=x2+2x=(x+1)2﹣1,此抛物线的顶点坐标为(﹣1,﹣1),
把点(﹣1,﹣1)向左平移2个单位长度,再向下平移3个单位长度后所得对应点的坐标为(﹣3,﹣4),所以平移后得到的抛物线的解析式为y=(x+3)2﹣4.
故答案为:y=(x+3)2﹣4.
17.解:∵AC与BD所成的锐角为45°,
∴根据四边形面积公式,得四边形ABCD的面积S=AC×BD×sin45°,
设AC=x,则BD=12﹣x,
所以S=x(12﹣x)×=﹣(x﹣6)2+9,
所以当x=6,S有最大值9.
故答案为:9.
18.解:作MG⊥DC于G,如图所示:
设MN=y,PC=x,
根据题意得:GN=5,MG=|10﹣2x|,
在Rt△MNG中,由勾股定理得:MN2=MG2+GN2,
即y2=52+(10﹣2x)2.
∵0<x<10,
∴当10﹣2x=0,即x=5时,y2最小值=25,
∴y最小值=5.即MN的最小值为5;
故答案为:5.
19.解:∵抛物线y=ax2﹣10ax+8=a(x﹣5)2﹣25a+8,
∴该抛物线的顶点的横坐标是x=5,当x=0时,y=8,
∴点D的坐标为:(0,8),
∴OD=8,
∵抛物线y=ax2﹣10ax+8(a>0)经过点C、D,CD∥AB∥x轴,
∴CD=5×2=10,
∴AD=10,
∵∠AOD=90°,OD=8,AD=10,
∴AO===6,
∵AB=10,
∴OB=10﹣AO=10﹣6=4,
∴点B的坐标为(4,0),
故答案为:(4,0)
20.解:∵y=﹣2x2﹣4x+1=﹣2(x+1)2+3.
∴该函数的图象的顶点坐标是(﹣1,3),对称轴为直线x=﹣1,抛物线开口方向向下,
∴当x<﹣1时,y随x的增大而增大,当x>﹣1时,y随x的增大而减小.
21.解:(1)点A、C的坐标分别为:(﹣2,0)、(0,3),
将点A、C的坐标代入抛物线表达式得:,解得:,
故抛物线的表达式为:y=﹣x2+x+3;
(2)存在,理由:
作点D关于对称轴的对称轴D′(﹣1,2),连接BD′交抛物线对称轴与点P,则点P为所求,
将点B、D′的坐标代入一次函数表达式:y=kx+b并解得:
直线BD′的函数表达式为:y=﹣x+,
抛物线的对称轴为:x=,当x=时,y=,
故点P(,);
(3)设点N(m,0),则点M、Q的坐标分别为:(m,m+1)、(m,﹣m2+m+3),
则QM=|﹣m2+m+3﹣m﹣1|=|﹣m2+2|,
3MN=3(m+1),
∵QM=3MN,即|﹣m2+2|=3(m+1),
解得:m=﹣2或﹣1或5(舍去﹣2),
故点Q坐标为(﹣1,2)或(5,﹣7).
22.解:(1)物线y=ax2+2x+c与y轴交于点A(0,6),则c=6,
将点B(6,0)代入函数表达式得:0=36a+12+6,
解得:a=﹣,
故抛物线的表达式为:y=﹣x2+2x+6,
∴函数的对称轴为:x=2,顶点坐标为(2,8);
(2)设点M(m,n),n=﹣m2+2m+6,点N(s,0),
①当AB是平行四边形的一条边时,
点A向右、向下均平移6个单位得到B,
同理点N右、向下均平移6个单位得到M,
故:s+6=m,0﹣6=n,
解得:m=2±2,
故点M的坐标为(2﹣2,﹣6)或(2+2,﹣6);
②当AB是平行四边形的对角线时,
则AB的中点即为MN的中点,则
s+m=6,n+0=6,
解得:m=4,
故点M的坐标为(4,6),
综上,点M的坐标为(2﹣2,﹣6)或(2+2,﹣6)或(4,6).
(3)如下图,过点P作PG∥y轴交AB于点G,作PH⊥AB交于点H,
∵OA=OB=6,则∠OAB=∠OBA=45°,
∵PG∥y轴,则∠PGH=∠OAB=45°,
直线AB的表达式为:y=﹣x+6,
设点P(x,﹣x2+2x+6),则G(x,﹣x+6),
d=PH=PG=(﹣x2+2x+6+x﹣6)=(﹣x2+3x),
当x=3时,d取得最大值,此时点P(3,).
23.解:(1)二次函数y=ax2+bx﹣6的图象经过点C(8,﹣6),点A(2,0),
∴,
∴,
∴二次函数的解析式为y=﹣x2+4x﹣6,
∴抛物线的对称轴为x=﹣=4,
∴D(4,0);
当y=0时,则﹣x2+4x﹣6=0,
∴x=2(点A的横坐标)或x=6,
∴B(6,0);
(2)由(1)知,D(4,0),
∵C(8,﹣6),
∴直线CD的解析式为y=﹣x+6①,
由(1)知,二次函数的解析式为y=﹣x2+4x﹣6②,
联立①②解得,或(点C的纵横坐标),
∴点E(3,),
如图1,过点B作BF∥y轴交CD于F,
由(1)知,B(6,0),
∴F(6,﹣3),
∴S△EBC=BF |xC﹣xE|=×3×|8﹣3|=;
(3)设点P的纵坐标为m,由(1)知,B(6,0),D(4,0),
∵C(8,﹣6),
∴S△DBC=BD |yC|=(6﹣4)×6=6,
∵S△ABP=S△DBC,
∴S△ABP=×6=3,
∵A(2,0),B(6,0),
∴S△ABP=AB |yP|=(6﹣2)|m|=2|m|=3,
∴m=±,
当m=时,﹣x2+4x﹣6=,x=3或x=5,
∴P(3,)或(5,),
当m=﹣时,﹣x2+4x﹣6=﹣,x=4﹣或x=4+,
∴P(4﹣,﹣)或(4+,﹣),即:P(3,)或(5,)或(4﹣,﹣)或(4+,﹣).
24.解:(1)抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),
故﹣3a=1,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+3…①;
(2)①当点P在第一象限时,如下图左图:
过点C作AP的平行线,过点B作AP的平行线交y轴于点H,
当GH=CG时,即点G是CH的中点时,则S△BAP=S△CAP,
设点P(m,﹣m2+2m+3),
将点P、A的坐标代入一次函数表达式:y=kx+b并解得:
直线PA的表达式为:y=(3﹣m)x+(3﹣m),则点G(0,3﹣m),
同理BH的表达式为:y=(3﹣m)x﹣3×(3﹣m),则点H(0,3m﹣9),
点G是CH的中点,则2(3﹣m)=3+3m﹣9,解得:m=,
故点P(,);
②当点P在第四象限时,如上图右侧图,
S△BAP=S△CAP,则点B、C到直线AP的距离相等,
则CB∥AP即满足条件,
同理可得:直线BC的表达式为:y=﹣x+3,
同理可得:直线AP的表达式为:y=﹣x﹣1…②,
联立①②并解得:x=4,故点P(4,﹣5),
③当点P在二、三象限时,点B、C到直线AP的距离不相等,故点P不存在;
综上,点P的坐标为:(,)或(4,﹣5);
(3)当以EF为直径的⊙R与x轴相切时,直线x上存在点P即切点,使∠EPF=90°,
当⊙R与x轴相交时,在x轴上存在点P(即交点),使∠EPF=90°,当⊙R与x轴相离时,不存在点P.
如下图,⊙R与x轴相切时,切点为P,
设:点E、F的坐标分别为:(x1,y1)、(x2,y2),
当平移后的抛物线顶点横坐标为m时,则抛物线向右平移了m﹣1个单位,相应纵坐标向上平移了2(m﹣1)个单位,则平移后抛物线的表达式为:y=﹣(x﹣m)2+2m+2,
将上式与y=2x﹣1联立并整理得:x2﹣(2m+2)x+m2﹣2m﹣3=0,
则x1+x2=2m+2,x1x2=m2﹣2m﹣3,
则y1+y2=2(x1+x2)﹣2=4m﹣6,则点R(m﹣1,2m﹣3),
则(x1﹣x2)2=(x1+x2)2﹣4x1x2=16,
PR=EF,即:EF2=4PR2,
EF2=(x1﹣x2)2+(y1﹣y2)2=5(x1﹣x2)2=5×16=4PR2=4[(2m﹣3)2]
解得:m=,
故m的范围是:≤m≤.
25.解:(1)当x=0时,y=ax2+bx+6=6,则C(0,6),
设抛物线的解析式为y=a(x+1)(x﹣6),
把C(0,6)代入得a 1 (﹣6)=6,解得a=﹣1,
∴抛物线的解析式为y=﹣(x+1)(x﹣6),即y=﹣x2+5x+6;
(2)连接AC,与对称轴交点即为所求点M,
设AC所在直线的解析式为y=mx+n,
将A(6,0),C(0,6)代入,得:,
解得:,
则AC所在直线解析式为y=﹣x+6,
又y=﹣x2+5x+6=﹣(x﹣)2+,
∴抛物线的对称轴为直线x=,
在直线y=﹣x+6中当x=时,y=,
则M的坐标为(,);
(3)设P点坐标为(x,﹣x2+5x+6),
存在4个点P,使△ACP为直角三角形.
PC2=x2+(﹣x2+5x)2,PA2=(x﹣6)2+(﹣x2+5x+6)2,AC2=62+62=72,
当∠PAC=90°,∵PA2+AC2=PC2,
∴(x﹣6)2+(﹣x2+5x+6)2+72=x2+(﹣x2+5x)2,
整理得x2﹣4x﹣12=0,解得x1=6(舍去),x2=﹣2,此时P点坐标为(﹣2,﹣8);
当∠PCA=90°,∵PC2+AC2=PA2,
72+x2+(﹣x2+5x)2=(x﹣6)2+(﹣x2+5x+6)2,
整理得x2﹣4x=0,解得x1=0(舍去),x2=4,此时P点坐标为(4,10);
当∠APC=90°,∵PA2+AC2=PC2,
∴(x﹣6)2+(﹣x2+5x+6)2+x2+(﹣x2+5x)2=72,
整理得x3﹣10x2+20x+24=0,
x3﹣10x2+24x﹣4x+24=0,
x(x2﹣10x+24)﹣4(x﹣6)=0,
x(x﹣4)(x﹣6)﹣4(x﹣6)=0,
(x﹣6)(x2﹣4x﹣4)=0,
而x﹣6≠0,
所以x2﹣4x﹣4=0,解得x1=2+2,x2=2﹣2,
此时P点坐标为(2+2,4+2)或(2﹣2,4﹣2);
综上所述,符合条件的点P的坐标为(﹣2,﹣8)或(4,10)或(2+2,4+2)或(2﹣2,4﹣2).
26.解:(1)∵抛物线y=2x2﹣2x﹣3过(0,﹣3),
∴设其衍生抛物线为y=ax2﹣3,
∵y=2x2﹣2x﹣3=2(x﹣)2﹣,
∴衍生抛物线为y=ax2﹣3过抛物线y=2x2﹣2x﹣3的顶点(,﹣),
∴﹣=a﹣3,
解得 a=﹣2,
∴衍生抛物线为y=﹣2x2﹣3.
设衍生直线为y=kx+b,
∵y=kx+b过(0,﹣3),(1,﹣4),
∴,
∴,
∴衍生直线为y=﹣x﹣3.
故答案是:y=﹣2x2﹣3;y=﹣x﹣3;
(2)∵衍生抛物线和衍生直线两交点分别为原抛物线与衍生抛物线的顶点,
∴将y=﹣2x2+1和y=﹣2x+1联立,得,
解得或,
∵衍生抛物线y=﹣2x2+1的顶点为(0,1),
∴原抛物线的顶点为(1,﹣1).
设原抛物线为y=a(x﹣1)2﹣1,
∵y=a(x﹣1)2﹣1过(0,1),
∴1=a(0﹣1)2﹣1,
解得 a=2,
∴原抛物线为y=2x2﹣4x+1.
(3)∵N(0,﹣3),
∴MN绕点N旋转到与x轴平行后,解析式为y=﹣3,
∴再沿y轴向上平移1个单位得的直线n解析式为y=﹣2.
设点P坐标为(x,﹣2),
∵O(0,0),M(,﹣),
∴OM2=(xM﹣xO)2+(yO﹣yM)2=+=,
OP2=(xP﹣xO)2+(yO﹣yP)2=x2+4,
MP2=(xP﹣xM)2+(yP﹣yM)2=(x﹣1)2+4=x2﹣x+.
①当OM2=OP2+MP2时,有=x2+4+x2﹣x+,
解得x=2或x=﹣,即P(2,﹣2)或P(﹣,﹣2).
②当OP2=OM2+MP2时,有x2+4=17+x2﹣x+,
解得 x=11,即P(11,﹣2).
③当MP2=OP2+OM2时,有x2﹣x+=x2+4+17,
解得 x=﹣14,即P(﹣14,﹣2).
综上所述,当P为(2,﹣2)或P(﹣,﹣2)或(11,﹣2)或(﹣14,﹣2)时,△POM为直角三角形.
1.下列函数关系中,是二次函数的是( )
A.在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
B.当距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长C与边长a之间的关系
D.半圆面积S与半径R之间的关系
2.在同一平面直角坐标系中,函数y=2x2+kx与y=kx+k(k≠0)的图象大致是( )
A. B. C. D.
3.如图,在4×4的网格中,每一个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点,以O为坐标原点建立如图所示的平面直角坐标系.若抛物线y=x2+bx+c的图象至少经过图中(4×4的网格中)的三个格点,并且至少一个格点在x轴上,则符合要求的抛物线一定不经过的格点坐标为( )
A.(1,3) B.(2,3) C.(1,4) D.(2,4)
4.若函数y=ax2﹣2x+a的图象与坐标轴只有1个交点,则a的取值范围是( )
A.a≥1 B.a>1或a=0
C.a≥1或a=0 D.a>1或a=0或a<﹣1
5.已知抛物线y=ax2+bx+c(a<0)过A(﹣2,0)、B(0,0)、C(﹣3,y1)、D(2,y2)四点,则y1与y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
6.如图,点A(m,5),B(n,2)是抛物线C1:y=x2﹣2x+3上的两点,将抛物线C1向左平移,得到抛物线C2,点A,B的对应点分别为点A',B'.若曲线段AB扫过的面积为9(图中的阴影部分),则抛物线C2的解析式是( )
A.y=(x﹣5)2+1 B.y=(x﹣2)2+4
C.y=(x+1)2+1 D.y=(x+2)2﹣2
7.若min{a,b,c}表示a,b,c三个数中的最小值,当y=min{x2,x+2,8﹣x}(x≥0)时,则y的最大值是( )
A.4 B.5 C.6 D.7
8.已知函数y=kx2﹣(k+2)x+2(k是常数),下列说法:①函数图象必过第一、二象限; ②当函数图象与坐标轴只有两个交点时,k=0;③当k<﹣2时,抛物线顶点在第一象限;④若k>0,则当x<时,y随着x的增大而减小,其中正确的有( )
A.①②③ B.①③④ C.②④ D.①③
9.已知抛物线y=ax2+3x+c(a,c为常数,且a≠0)经过点(﹣1,﹣1),(0,3),有下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小;③3是方程ax2+2x+c=0的一个根;④当﹣1<x<3时,ax2+2x+c>0其中正确结论的个数是( )
A.1 B.2 C.3 D.4
10.如图,抛物线y=x+2交x轴于点A,B,交y轴于点C,当△ABC纸片上的点C沿着此抛物线运动时,则△ABC纸片随之也跟着移动,设纸片上BC的中点M坐标为(m,n),在此运动过程中,n与m的关系式是( )
A.n=(m﹣)2﹣ B.n=(m﹣)2
C.n=(m﹣)2﹣ D.n=(m﹣)2﹣
11.有一个矩形苗圃园,其中一边靠墙,另外边用长为20m的篱笆围成.已知墙长为15m,若平行于墙的一边长不小于8m,则这个苗圃园面积的最大值和最小值分别为( )
A.48m2,37.5m2 B.50m2,32m2
C.50m2,37.5m2 D.48m2,32m2
12.如图,抛物线y=ax2﹣x+4与直线y=x+b经过点A(2,0),且相交于另一点B;抛物线与y轴交于点C,与x轴交于另一点E;点N在线段AB上,过点N的直线交抛物线于点M,且MN∥y轴,连接AM、BM、BC、AC;当点N在线段AB上移动时(不与A、B重合),下列结论中正确的是( )
A.MN+BN<AB
B.∠BAC=∠BAE
C.∠ACB﹣∠ANM=∠ABC
D.四边形ACBM的最大面积为13
13.已知抛物线y=a(x﹣3)2+过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:
①抛物线的对称轴是直线x=3;
②点C在⊙D外;
③在抛物线上存在一点E,能使四边形ADEC为平行四边形;
④直线CM与⊙D相切.
正确的结论是( )
A.①③ B.①④ C.①③④ D.①②③④
14.二次函数y1=mx2、y2=nx2的图象如图所示,则m n(填“>”或“<”).
15.如果点A(﹣1,4)、B(m,4)在抛物线y=a(x﹣1)2+h上,那么m的值为 .
16.将抛物线y=x2+2x向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的表达式为 ;
17.如图,四边形的两条对角线AC、BD所成的锐角为45°,当AC+BD=12时,四边形ABCD的面积最大值是 .
18.如图,线段AB=10,点P在线段AB上,在AB的同侧分别以AP、BP为边长作正方形APCD和BPEF,点M、N分别是EF、CD的中点,则MN的最小值是 .
19.如图,在平面直角坐标系中,菱形ABCD的顶点A在x轴负半轴上,顶点B在x轴正半轴上.若抛物线y=ax2﹣10ax+8(a>0)经过点C、D,则点B的坐标为 .
20.已知二次函数y=﹣2x2﹣4x+1,先用配方法转化成y=a(x﹣h)2+k,再写出函数的顶点坐标、对称轴以及描述该函数的增减性.
21.如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式;
(2)点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
(3)连接AD并延长,过抛物线上一点Q(Q不与A重合)作QN⊥x轴,垂足为N,与射线交于点M,使得QM=3MN,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
22.如图,已知抛物线y=ax2+2x+c与y轴交于点A(0,6),与x轴交于点B(6,0),点P是线段AB上方抛物线上的一个动点.
(1)求这条抛物线的表达式及其顶点坐标;
(2)点M在抛物线上,点N在x轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标:若不存在,请说明理由;
(3)当点P从A点出发沿线段AB上方的抛物线向终点B移动时,点P到直线AB的距离为d,求d最大时点P的坐标.
23.综合与探究:
如图,二次函数y=ax2+bx﹣6的图象与x轴交于A,B两点,并经过点C(8,﹣6),对称轴交x轴于点D.已知点A坐标是(2,0).
(1)求点B和点D的坐标;
(2)连接并延长CD交抛物线于点E,连接BC,BE,求△EBC的面积;
(3)抛物线上有一个动点P,与A,B两点构成△ABP,是否存在S△ABP=S△DBC?若存在,请求出点P的坐标;若不存在,请说明理由.
24.已知抛物线y=ax2+bx+3与x轴交于A(﹣1,0)、B(3,0)两点.
(1)求抛物线解析式;
(2)抛物线与y轴交于点C,在抛物线上存在点P,使S△BAP=S△CAP,求P点坐标;
(3)已知直线l:y=2x﹣1,将抛物线沿y=2x﹣1方向平移,平移过程中与l相交于E、F两点.设平移过程中抛物线的顶点的横坐标为m,在x轴上存在一点P,使∠EPF=90°,求m的范围.
25.如图,抛物线y=ax2+bx+6与x轴交于点A(6,0),B(﹣1,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)若点M为该抛物线对称轴上一点,当CM+BM最小时,求点M的坐标.
(3)抛物线上是否存在点P,使△ACP为直角三角形?若存在,有几个?写出所有符合条件的点P的坐标;若不存在,说明理由.
26.已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=2x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=2x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
参考答案
1.解:A、y=kx+b,是一次函数,错误;
B、t=,是反比例函数,错误;
C、C=3a,是正比例函数,错误;
D、S=.是二次函数,正确;
故选:D.
2.解:当k>0时,函数y=kx+k的图象经过一、二、三象限;函数y=2x2+kx的开口向上,对称轴在y轴的左侧;
当k<0时,函数y=kx+k的图象经过二、三、四象限;函数y=2x2+kx的开口向上,对称轴在y轴的右侧,故C正确.
故选:C.
3.解:∵二次项系数为1,∴该抛物线开口向上
∵图象至少经过图中(4×4的网格中)的三个格点,且至少一个格点在x轴上,
∴结合二次函数的对称性分析如下:
选项A:若过(1,3),将点A坐标代入抛物线表达式并解得:
抛物线的表达式为:y=x2+bx+(2﹣b),
设抛物线过点(2,0),即当x=2时,y=4+2b+2﹣b=0,解得:b=﹣6,
抛物线的表达式为:y=x2﹣6x+8=(x﹣2)(x﹣4),
即抛物线还过点(2,0)、(4,0),不符合题意;
选项B:若过(2,3),还可过点(3,1),将这个点的坐标代入y=x2+bx+c并解得:y=x2﹣7x+13,
若同时过x轴上的可能的格点(4,0),当x=4时,y=1,故B符合题意;
故选:B.
4.解:当a=0时,y=﹣2x,该函数与坐标轴有1个交点;
当a≠0时,△=4﹣4a2<0时,图象与坐标轴只有1个交点,解得:a>1或a<﹣1;
故选:D.
5.解:抛物线y=ax2+bx+c(a<0)过A(﹣2,0)、B(0,0),
则函数的对称轴为:x=﹣1,
x=﹣3比x=2离对称轴近,故y1>y2,
故选:C.
6.解:y=x2﹣2x+3=(x﹣2)2+1.
∵曲线段AB扫过的面积为9(图中的阴影部分),点A(m,5),B(n,2)
∴3BB′=9,
∴BB′=3,
即将函数y=(x﹣2)2+1的图象沿x轴向左平移3个单位长度得到一条新函数的图象,
∴新图象的函数表达式是y=(x+1)2+1.
故选:C.
7.解:解方程x2=x+2得:x=2或x=﹣1,(因为x≥0,x=﹣1舍去),
解方程x+2=8﹣x得:x=3,
解方程x2=8﹣x得:x=,(因为x≥0,x=舍去),
当0≤x≤2时,y的最大值是点A的纵坐标;
当2<x≤时,y的最大值是点B的纵坐标;
当x>时,y的最大值是点C的纵坐标;
如图所示:
y最大=3+2=5,
即y的最大值是5,
故选:B.
8.解:①当k=0时,函数为y=﹣x+2,函数图象经过第一、二、四象限;当k≠0时,△=(k+2)2﹣8k=(k﹣2)2≥0;
k>0时,抛物线开口向上,并且与x轴有交点,函数图象必过第一二象限;k<0时,抛物线开口向下,与y轴相交于y轴正半轴,函数图象必过第一二象限;所以函数图象必经过第一、二象限,故符合题意;
②当k=0时,此函数是不平行于坐标轴的直线,所以,函数与坐标轴有两个交点,当k≠0时,函数是抛物线,必与y轴相交,△=(k+2)2﹣8k=(k﹣2)2≥0,抛物线与x轴有一个(k=2时)或两个交点,此时函数与坐标轴有两个到三个交点,故不符合题意;
③当k<﹣2时,对称轴x=>0,顶点纵坐标==﹣>0,故抛物线顶点在第一象限,符合题意;
④若k>0,抛物线的对称轴为:x=﹣=,则当x<时,y随着x的增大而减小,符合题意;
故选:B.
9.解:把点(﹣1,﹣1),(0,3)代入y=ax2+3x+c得:
∴
∴y=﹣x2+3x+3
∴①ac<0正确;
该抛物线的对称轴为:,
∴②当x>1时,y的值随x值的增大而减小是错误的;
方程ax2+2x+c=0可化为:方程ax2+3x+c=x,
把x=3代入y=﹣x2+3x+3得y=3,
∴﹣x2+2x+3=0,
故③正确;
∴(3,3)在该抛物线上,
又∵抛物线y=ax2+3x+c(a,c为常数,且a≠0)经过点(﹣1,﹣1),
∴抛物线y=ax2+3x+c与y=x的交点为(﹣1,﹣1)和(3,3),
当﹣1<x<3时,ax2+3x+c>x,即ax2+2x+c>0
④当﹣1<x<3时,ax2+2x+c>0,故④正确.
综上,①③④正确.
故选:C.
10.解:∵抛物线y=x+2交x轴于点A,B,交y轴于点C,
∴点B的坐标为(4,0),点C的坐标为(0,2),
∴BC的中点M坐标为(,),即点M坐标为(2,1).
∵点C沿着此抛物线运动,点M也随之运动,点M的运动轨迹是抛物线,且经过(2,1),(6,﹣1)
∴设抛物线的解析式为y=x2+bx+c,
则有,解得
∴m,n满足,n=m2﹣m+8=(m﹣)2﹣,
故选:D.
11.解:设平行于墙的一边长为xm,苗圃园面积为Sm2,则
S=x×(20﹣x)
=﹣(x2﹣20x)
=﹣(x﹣10)2+50 (8≤x≤15)
∵﹣<0
∴S有最大值,x=10>8时,S最大=50
∵墙长为15m
∴当x=15时,S最小
S最小=15××(20﹣15)=37.5
∴这个苗圃园面积的最大值和最小值分别为50m2,37.5m2.
故选:C.
12.解:将点A(2,0)代入抛物线y=ax2﹣x+4与直线y=x+b
解得:a=,b=﹣,
设:M点横坐标为m,则M(m,m2﹣m+4)、N(m,m﹣),
其它点坐标为A(2,0)、B(5,4)、C(0,4),
则AB=BC=5,则∠CAB=∠ACB,
∴△ABC是等腰三角形.
A、当MN过对称轴的直线时,此时点M、N的坐标分别为(,﹣)、(,),
由勾股定理得:BN=,而MN=,
BN+MN=5=AB,
故本选项错误;
B、∵BC∥x轴(B、C两点y坐标相同),
∴∠BAE=∠CBA,而△ABC是等腰三角形不是等边三角形,
∠CBA≠∠BCA,
∴∠BAC=∠BAE不成立,
故本选项错误;
C、如上图,过点A作AD⊥BC、BF⊥AC,
∵△ABC是等腰三角形,
∴BF是∠ABC的平分线,
易证:∠CAD=∠ABF=ABC,
而∠ACB﹣∠ANM=∠CAD=ABC,
故本选项正确;
D、S四边形ACBM=S△ABC+S△ABM,
S△ABC=10,
S△ABM=MN (xB﹣xA)=﹣m2+7m﹣10,其最大值为,
故S四边形ACBM的最大值为10+=12.25,
故本选项错误.
故选:C.
13.解:由抛物线y=a(x﹣3)2+可知:抛物线的对称轴x=3,故①正确;
∵抛物线y=a(x﹣3)2+过点C(0,4),
∴4=9a+,解得:a=﹣,
∴抛物线的解析式为y=﹣(x﹣3)2+,
令y=0,则﹣(x﹣3)2+=0,解得:x=8或x=﹣2,
∴A(﹣2,0),B(8,0);
∴AB=10,
∴AD=5,
∴OD=3
∵C(0,4),
∴CD==5,
∴CD=AD,
∴点C在圆上,故②错误;
过点C作CE∥AB,交抛物线于E,
∵C(0,4),
代入y=﹣(x﹣3)2+得:4=﹣(x﹣3)2+,
解得:x=0或x=6,
∴CE=6,
∴AD≠CE,
∴四边形ADEC不是平行四边形,故③错误;
由抛物线y=a(x﹣3)2+可知:M(3,),
∵C(0,4),
∴直线CM为y=x+4,直线CD为:y=﹣x+4,
∴CM⊥CD,
∵CD=AD=5,
∴直线CM与⊙D相切,故④正确;
故选:B.
14.解:根据抛物线的开口大小与二次函数的二次项系数的关系:系数越大,开口越小,
故m>n,
故答案为>.
15.解:由点A(﹣1,4)、B(m,4)在抛物线y=a(x﹣1)2+h上,得
(﹣1,4)与(m,4)关于对称轴x=1对称,
m﹣1=1﹣(﹣1),
解得m=3,
故答案为:3.
16.解:y=x2+2x=(x+1)2﹣1,此抛物线的顶点坐标为(﹣1,﹣1),
把点(﹣1,﹣1)向左平移2个单位长度,再向下平移3个单位长度后所得对应点的坐标为(﹣3,﹣4),所以平移后得到的抛物线的解析式为y=(x+3)2﹣4.
故答案为:y=(x+3)2﹣4.
17.解:∵AC与BD所成的锐角为45°,
∴根据四边形面积公式,得四边形ABCD的面积S=AC×BD×sin45°,
设AC=x,则BD=12﹣x,
所以S=x(12﹣x)×=﹣(x﹣6)2+9,
所以当x=6,S有最大值9.
故答案为:9.
18.解:作MG⊥DC于G,如图所示:
设MN=y,PC=x,
根据题意得:GN=5,MG=|10﹣2x|,
在Rt△MNG中,由勾股定理得:MN2=MG2+GN2,
即y2=52+(10﹣2x)2.
∵0<x<10,
∴当10﹣2x=0,即x=5时,y2最小值=25,
∴y最小值=5.即MN的最小值为5;
故答案为:5.
19.解:∵抛物线y=ax2﹣10ax+8=a(x﹣5)2﹣25a+8,
∴该抛物线的顶点的横坐标是x=5,当x=0时,y=8,
∴点D的坐标为:(0,8),
∴OD=8,
∵抛物线y=ax2﹣10ax+8(a>0)经过点C、D,CD∥AB∥x轴,
∴CD=5×2=10,
∴AD=10,
∵∠AOD=90°,OD=8,AD=10,
∴AO===6,
∵AB=10,
∴OB=10﹣AO=10﹣6=4,
∴点B的坐标为(4,0),
故答案为:(4,0)
20.解:∵y=﹣2x2﹣4x+1=﹣2(x+1)2+3.
∴该函数的图象的顶点坐标是(﹣1,3),对称轴为直线x=﹣1,抛物线开口方向向下,
∴当x<﹣1时,y随x的增大而增大,当x>﹣1时,y随x的增大而减小.
21.解:(1)点A、C的坐标分别为:(﹣2,0)、(0,3),
将点A、C的坐标代入抛物线表达式得:,解得:,
故抛物线的表达式为:y=﹣x2+x+3;
(2)存在,理由:
作点D关于对称轴的对称轴D′(﹣1,2),连接BD′交抛物线对称轴与点P,则点P为所求,
将点B、D′的坐标代入一次函数表达式:y=kx+b并解得:
直线BD′的函数表达式为:y=﹣x+,
抛物线的对称轴为:x=,当x=时,y=,
故点P(,);
(3)设点N(m,0),则点M、Q的坐标分别为:(m,m+1)、(m,﹣m2+m+3),
则QM=|﹣m2+m+3﹣m﹣1|=|﹣m2+2|,
3MN=3(m+1),
∵QM=3MN,即|﹣m2+2|=3(m+1),
解得:m=﹣2或﹣1或5(舍去﹣2),
故点Q坐标为(﹣1,2)或(5,﹣7).
22.解:(1)物线y=ax2+2x+c与y轴交于点A(0,6),则c=6,
将点B(6,0)代入函数表达式得:0=36a+12+6,
解得:a=﹣,
故抛物线的表达式为:y=﹣x2+2x+6,
∴函数的对称轴为:x=2,顶点坐标为(2,8);
(2)设点M(m,n),n=﹣m2+2m+6,点N(s,0),
①当AB是平行四边形的一条边时,
点A向右、向下均平移6个单位得到B,
同理点N右、向下均平移6个单位得到M,
故:s+6=m,0﹣6=n,
解得:m=2±2,
故点M的坐标为(2﹣2,﹣6)或(2+2,﹣6);
②当AB是平行四边形的对角线时,
则AB的中点即为MN的中点,则
s+m=6,n+0=6,
解得:m=4,
故点M的坐标为(4,6),
综上,点M的坐标为(2﹣2,﹣6)或(2+2,﹣6)或(4,6).
(3)如下图,过点P作PG∥y轴交AB于点G,作PH⊥AB交于点H,
∵OA=OB=6,则∠OAB=∠OBA=45°,
∵PG∥y轴,则∠PGH=∠OAB=45°,
直线AB的表达式为:y=﹣x+6,
设点P(x,﹣x2+2x+6),则G(x,﹣x+6),
d=PH=PG=(﹣x2+2x+6+x﹣6)=(﹣x2+3x),
当x=3时,d取得最大值,此时点P(3,).
23.解:(1)二次函数y=ax2+bx﹣6的图象经过点C(8,﹣6),点A(2,0),
∴,
∴,
∴二次函数的解析式为y=﹣x2+4x﹣6,
∴抛物线的对称轴为x=﹣=4,
∴D(4,0);
当y=0时,则﹣x2+4x﹣6=0,
∴x=2(点A的横坐标)或x=6,
∴B(6,0);
(2)由(1)知,D(4,0),
∵C(8,﹣6),
∴直线CD的解析式为y=﹣x+6①,
由(1)知,二次函数的解析式为y=﹣x2+4x﹣6②,
联立①②解得,或(点C的纵横坐标),
∴点E(3,),
如图1,过点B作BF∥y轴交CD于F,
由(1)知,B(6,0),
∴F(6,﹣3),
∴S△EBC=BF |xC﹣xE|=×3×|8﹣3|=;
(3)设点P的纵坐标为m,由(1)知,B(6,0),D(4,0),
∵C(8,﹣6),
∴S△DBC=BD |yC|=(6﹣4)×6=6,
∵S△ABP=S△DBC,
∴S△ABP=×6=3,
∵A(2,0),B(6,0),
∴S△ABP=AB |yP|=(6﹣2)|m|=2|m|=3,
∴m=±,
当m=时,﹣x2+4x﹣6=,x=3或x=5,
∴P(3,)或(5,),
当m=﹣时,﹣x2+4x﹣6=﹣,x=4﹣或x=4+,
∴P(4﹣,﹣)或(4+,﹣),即:P(3,)或(5,)或(4﹣,﹣)或(4+,﹣).
24.解:(1)抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),
故﹣3a=1,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+3…①;
(2)①当点P在第一象限时,如下图左图:
过点C作AP的平行线,过点B作AP的平行线交y轴于点H,
当GH=CG时,即点G是CH的中点时,则S△BAP=S△CAP,
设点P(m,﹣m2+2m+3),
将点P、A的坐标代入一次函数表达式:y=kx+b并解得:
直线PA的表达式为:y=(3﹣m)x+(3﹣m),则点G(0,3﹣m),
同理BH的表达式为:y=(3﹣m)x﹣3×(3﹣m),则点H(0,3m﹣9),
点G是CH的中点,则2(3﹣m)=3+3m﹣9,解得:m=,
故点P(,);
②当点P在第四象限时,如上图右侧图,
S△BAP=S△CAP,则点B、C到直线AP的距离相等,
则CB∥AP即满足条件,
同理可得:直线BC的表达式为:y=﹣x+3,
同理可得:直线AP的表达式为:y=﹣x﹣1…②,
联立①②并解得:x=4,故点P(4,﹣5),
③当点P在二、三象限时,点B、C到直线AP的距离不相等,故点P不存在;
综上,点P的坐标为:(,)或(4,﹣5);
(3)当以EF为直径的⊙R与x轴相切时,直线x上存在点P即切点,使∠EPF=90°,
当⊙R与x轴相交时,在x轴上存在点P(即交点),使∠EPF=90°,当⊙R与x轴相离时,不存在点P.
如下图,⊙R与x轴相切时,切点为P,
设:点E、F的坐标分别为:(x1,y1)、(x2,y2),
当平移后的抛物线顶点横坐标为m时,则抛物线向右平移了m﹣1个单位,相应纵坐标向上平移了2(m﹣1)个单位,则平移后抛物线的表达式为:y=﹣(x﹣m)2+2m+2,
将上式与y=2x﹣1联立并整理得:x2﹣(2m+2)x+m2﹣2m﹣3=0,
则x1+x2=2m+2,x1x2=m2﹣2m﹣3,
则y1+y2=2(x1+x2)﹣2=4m﹣6,则点R(m﹣1,2m﹣3),
则(x1﹣x2)2=(x1+x2)2﹣4x1x2=16,
PR=EF,即:EF2=4PR2,
EF2=(x1﹣x2)2+(y1﹣y2)2=5(x1﹣x2)2=5×16=4PR2=4[(2m﹣3)2]
解得:m=,
故m的范围是:≤m≤.
25.解:(1)当x=0时,y=ax2+bx+6=6,则C(0,6),
设抛物线的解析式为y=a(x+1)(x﹣6),
把C(0,6)代入得a 1 (﹣6)=6,解得a=﹣1,
∴抛物线的解析式为y=﹣(x+1)(x﹣6),即y=﹣x2+5x+6;
(2)连接AC,与对称轴交点即为所求点M,
设AC所在直线的解析式为y=mx+n,
将A(6,0),C(0,6)代入,得:,
解得:,
则AC所在直线解析式为y=﹣x+6,
又y=﹣x2+5x+6=﹣(x﹣)2+,
∴抛物线的对称轴为直线x=,
在直线y=﹣x+6中当x=时,y=,
则M的坐标为(,);
(3)设P点坐标为(x,﹣x2+5x+6),
存在4个点P,使△ACP为直角三角形.
PC2=x2+(﹣x2+5x)2,PA2=(x﹣6)2+(﹣x2+5x+6)2,AC2=62+62=72,
当∠PAC=90°,∵PA2+AC2=PC2,
∴(x﹣6)2+(﹣x2+5x+6)2+72=x2+(﹣x2+5x)2,
整理得x2﹣4x﹣12=0,解得x1=6(舍去),x2=﹣2,此时P点坐标为(﹣2,﹣8);
当∠PCA=90°,∵PC2+AC2=PA2,
72+x2+(﹣x2+5x)2=(x﹣6)2+(﹣x2+5x+6)2,
整理得x2﹣4x=0,解得x1=0(舍去),x2=4,此时P点坐标为(4,10);
当∠APC=90°,∵PA2+AC2=PC2,
∴(x﹣6)2+(﹣x2+5x+6)2+x2+(﹣x2+5x)2=72,
整理得x3﹣10x2+20x+24=0,
x3﹣10x2+24x﹣4x+24=0,
x(x2﹣10x+24)﹣4(x﹣6)=0,
x(x﹣4)(x﹣6)﹣4(x﹣6)=0,
(x﹣6)(x2﹣4x﹣4)=0,
而x﹣6≠0,
所以x2﹣4x﹣4=0,解得x1=2+2,x2=2﹣2,
此时P点坐标为(2+2,4+2)或(2﹣2,4﹣2);
综上所述,符合条件的点P的坐标为(﹣2,﹣8)或(4,10)或(2+2,4+2)或(2﹣2,4﹣2).
26.解:(1)∵抛物线y=2x2﹣2x﹣3过(0,﹣3),
∴设其衍生抛物线为y=ax2﹣3,
∵y=2x2﹣2x﹣3=2(x﹣)2﹣,
∴衍生抛物线为y=ax2﹣3过抛物线y=2x2﹣2x﹣3的顶点(,﹣),
∴﹣=a﹣3,
解得 a=﹣2,
∴衍生抛物线为y=﹣2x2﹣3.
设衍生直线为y=kx+b,
∵y=kx+b过(0,﹣3),(1,﹣4),
∴,
∴,
∴衍生直线为y=﹣x﹣3.
故答案是:y=﹣2x2﹣3;y=﹣x﹣3;
(2)∵衍生抛物线和衍生直线两交点分别为原抛物线与衍生抛物线的顶点,
∴将y=﹣2x2+1和y=﹣2x+1联立,得,
解得或,
∵衍生抛物线y=﹣2x2+1的顶点为(0,1),
∴原抛物线的顶点为(1,﹣1).
设原抛物线为y=a(x﹣1)2﹣1,
∵y=a(x﹣1)2﹣1过(0,1),
∴1=a(0﹣1)2﹣1,
解得 a=2,
∴原抛物线为y=2x2﹣4x+1.
(3)∵N(0,﹣3),
∴MN绕点N旋转到与x轴平行后,解析式为y=﹣3,
∴再沿y轴向上平移1个单位得的直线n解析式为y=﹣2.
设点P坐标为(x,﹣2),
∵O(0,0),M(,﹣),
∴OM2=(xM﹣xO)2+(yO﹣yM)2=+=,
OP2=(xP﹣xO)2+(yO﹣yP)2=x2+4,
MP2=(xP﹣xM)2+(yP﹣yM)2=(x﹣1)2+4=x2﹣x+.
①当OM2=OP2+MP2时,有=x2+4+x2﹣x+,
解得x=2或x=﹣,即P(2,﹣2)或P(﹣,﹣2).
②当OP2=OM2+MP2时,有x2+4=17+x2﹣x+,
解得 x=11,即P(11,﹣2).
③当MP2=OP2+OM2时,有x2﹣x+=x2+4+17,
解得 x=﹣14,即P(﹣14,﹣2).
综上所述,当P为(2,﹣2)或P(﹣,﹣2)或(11,﹣2)或(﹣14,﹣2)时,△POM为直角三角形.
