2021-2022学年湘教版九年级数学上册期末模拟试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版九年级数学上册期末模拟试卷(word版含答案) | 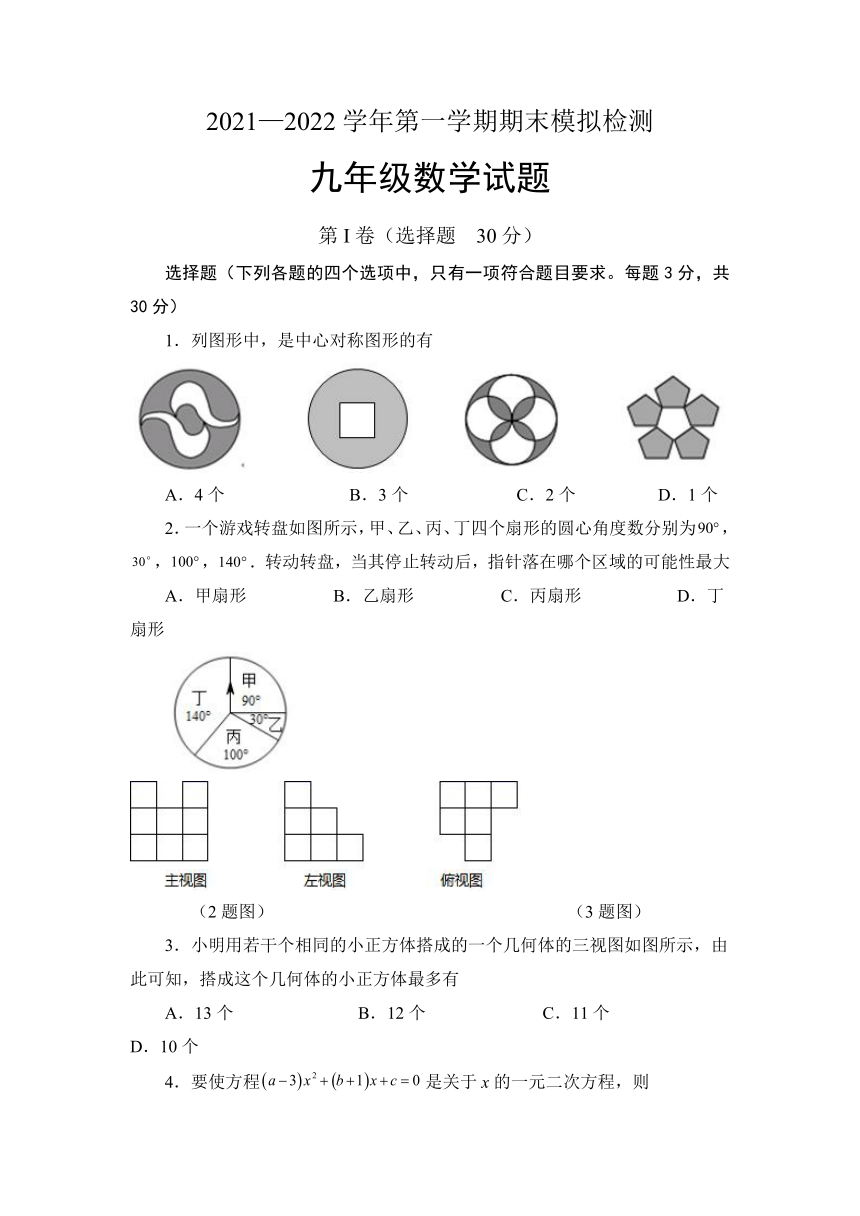 | |
| 格式 | doc | ||
| 文件大小 | 811.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 15:01:57 | ||
图片预览


文档简介
2021—2022学年第一学期期末模拟检测
九年级数学试题
第I卷(选择题 30分)
选择题(下列各题的四个选项中,只有一项符合题目要求。每题3分,共30分)
1.列图形中,是中心对称图形的有
A.4个 B.3个 C.2个 D.1个
2.一个游戏转盘如图所示,甲、乙、丙、丁四个扇形的圆心角度数分别为,,,.转动转盘,当其停止转动后,指针落在哪个区域的可能性最大
A.甲扇形 B.乙扇形 C.丙扇形 D.丁扇形
(2题图) (3题图)
3.小明用若干个相同的小正方体搭成的一个几何体的三视图如图所示,由此可知,搭成这个几何体的小正方体最多有
A.13个 B.12个 C.11个 D.10个
4.要使方程是关于x的一元二次方程,则
A.a≠0 B.a≠3
C.a≠1且b≠﹣1 D.a≠3且b≠﹣1且c≠0
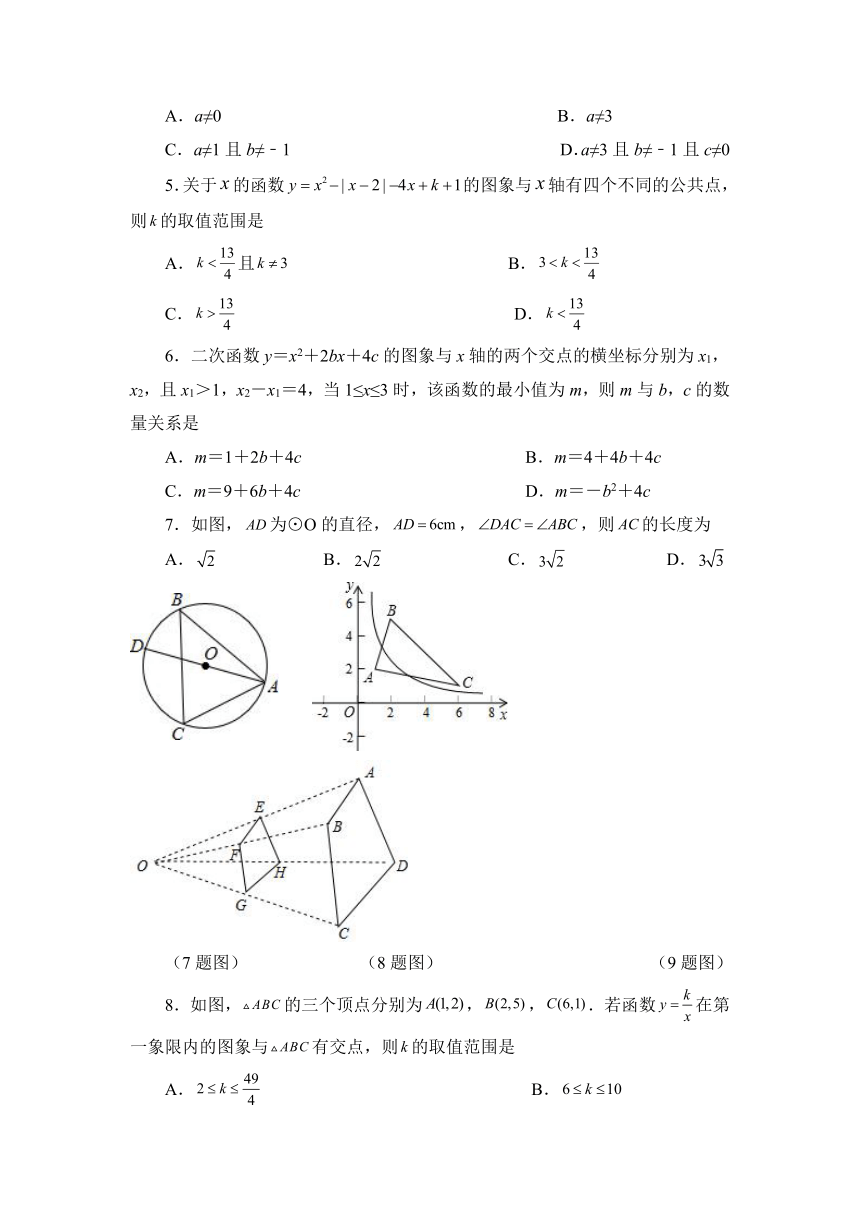
5.关于的函数的图象与轴有四个不同的公共点,则的取值范围是
A.且 B.
C. D.
6.二次函数y=x2+2bx+4c的图象与x轴的两个交点的横坐标分别为x1,x2,且x1>1,x2-x1=4,当1≤x≤3时,该函数的最小值为m,则m与b,c的数量关系是
A.m=1+2b+4c B.m=4+4b+4c
C.m=9+6b+4c D.m=-b2+4c
7.如图,为⊙O的直径,,,则的长度为
A. B. C. D.
(7题图) (8题图) (9题图)
8.如图,的三个顶点分别为,,.若函数在第一象限内的图象与有交点,则的取值范围是
A. B.
C. D.
9.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,则=
A. B. C. D.
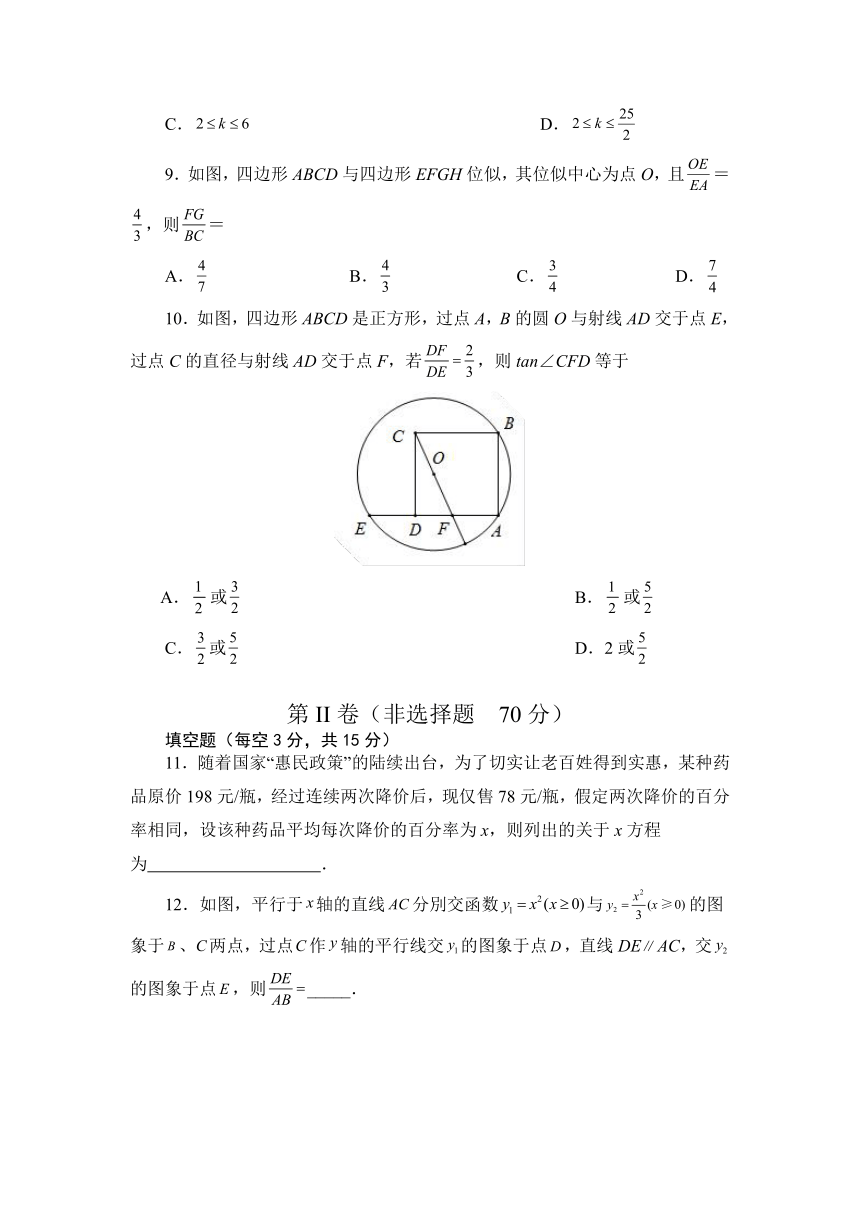
10.如图,四边形ABCD是正方形,过点A,B的圆O与射线AD交于点E,过点C的直径与射线AD交于点F,若,则tan∠CFD等于
或 B.或
C.或 D.2或
第II卷(非选择题 70分)
填空题(每空3分,共15分)
11.随着国家“惠民政策”的陆续出台,为了切实让老百姓得到实惠,某种药品原价198元/瓶,经过连续两次降价后,现仅售78元/瓶,假定两次降价的百分率相同,设该种药品平均每次降价的百分率为x,则列出的关于x方程为 .
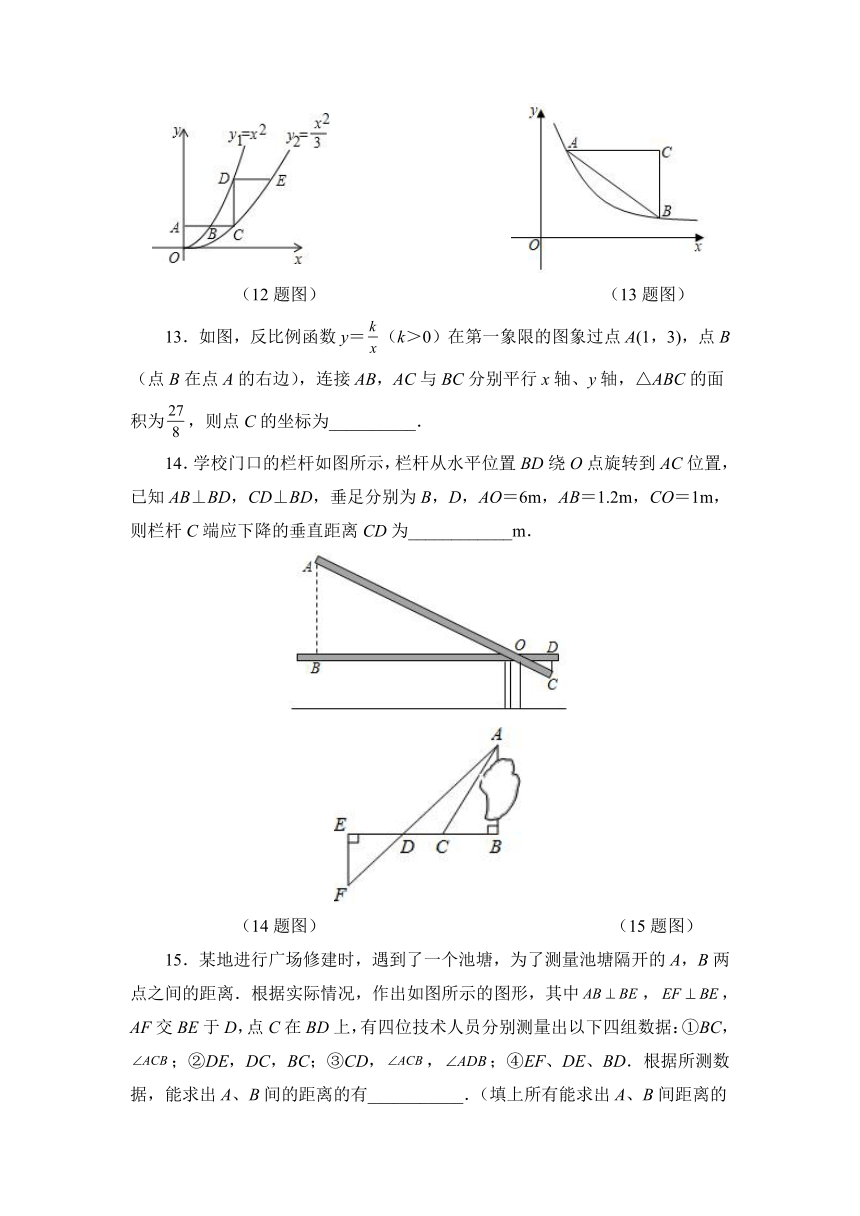
12.如图,平行于轴的直线分別交函数与的图象于、两点,过点作轴的平行线交的图象于点,直线DEAC,交的图象于点,则_____.
(12题图) (13题图)
13.如图,反比例函数y=(k>0)在第一象限的图象过点A(1,3),点B(点B在点A的右边),连接AB,AC与BC分别平行x轴、y轴,△ABC的面积为,则点C的坐标为__________.
14.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=6m,AB=1.2m,CO=1m,则栏杆C端应下降的垂直距离CD为____________m.
(14题图) (15题图)
15.某地进行广场修建时,遇到了一个池塘,为了测量池塘隔开的A,B两点之间的距离.根据实际情况,作出如图所示的图形,其中,,AF交BE于D,点C在BD上,有四位技术人员分别测量出以下四组数据:①BC,;②DE,DC,BC;③CD,,;④EF、DE、BD.根据所测数据,能求出A、B间的距离的有___________.(填上所有能求出A、B间距离的序号)
解答题(共55分)
16.(6分)(1)计算:
(2)解方程:
17.(6分)在一个不透明的布袋中放有三个分别标有数,,的乒乓球,它们的质地都相同.现从中任意摸出一个球记下所标的数字,将其放回袋中搅匀,再从袋子里任意摸出一个球记下所标的数字.
(1)请用画树状图法或列表法表示出所有可能的结果.
(2)求两次记下的数字的乘积为正数的概率.
18.(7分)如图,在平面直角坐标系中,已知的三个顶点的坐标分别为、、.
(1)与关于原点成中心对称,写出点、、的坐标;
(2)将绕点顺时针旋转得到,画出;
(3)求的面积.
19.(8分)如图,点在线段上,在的同侧作等腰和等腰,与、分别交于点、.
求证:(1);
(2).
20.(8分)如图,点O在△ABC的BC边上,⊙O经过点A、C,且与BC相交于点D.点E是下半圆弧的中点,连接AE交BC于点F,已知AB=BF.
(1)求证:AB是⊙O的切线;
(2)若OC=3,OF=1,求cos∠B的值.
21.(9分)如图,一次函数与反比例函数的图象交于,两点.
(1)求反比例函数的解析式和的值;
(2)根据图象直接写出不等式的的取值范围;
(3)求的面积.
22.(11分)已知抛物线过点.
(1)求抛物线的解析式;
(2)点A在直线上且在第一象限内,过A作轴于B,以为斜边在其左侧作等腰直角.
①若A与Q重合,求C到抛物线对称轴的距离;
②若C落在抛物线上,求C的坐标.
【参考答案】
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B D A B B C C A A B
二、填空题(每空3分,共30分)
11.198(1-x)2=78 12. 13.(4,3) 14.0.2 15.①③④
三、解答题(共55分)
16.(1)-5 (2)x=-4或x=-5
17.解:(1)列表如下:
-3 -5
-3
-5
由表格可知,共有种等可能的结果.
(2)由(1)知,共有种等可能的结果,
两次记下的数字的乘积为正数的情况有种,
两次记下的数字的乘积为正数的概率.
18.解:(1)如图,即为所求作,点,,;
(2)如图,即为所求作;
(3)的面积.
19.证明:(1)等腰和等腰,
,,
,,,
,,
,且,
∴
(2)∵
,且
∴,
20.解:(1)证明:连接OA、OE,
∵点E是下半圆弧的中点,OE过O,
∴OE⊥DC,
∴∠FOE=90°,
∴∠E+∠OFE=90°,
∵OA=OE,AB=BF,
∴∠BAF=∠BFA,∠E=∠OAE,
∵∠AFB=∠OFE,
∴∠OAE+∠BAF=90°,
即OA⊥AB,
∵OA为半径,
∴AB是⊙O的切线;
(2)解:设AB=x,则BF=x,OB=x+1,
∵OA=OC=3,
由勾股定理得:OB2=AB2+OA2,
∴(1+x)2=32+x2,
解得:x=4,
∴.
21.解:(1)在的图象上,
,
反比例函数的解析式是.
又∵在的图象上,
;
(2)由图像可知:当或时,;
(3),在函数的图象上,
,
解得:,
则一次函数的解析式是,
设直线与轴相交于点,则的坐标是.
∴
.
22.解:(1)将两点分别代入,得
解得.
所以抛物线的解析式是.
(2)①如图2,抛物线的对称轴是y轴,当点A与点重合时,,
作于H.
∵是等腰直角三角形,
∴和也是等腰直角三角形,
∴,
∴点C到抛物线的对称轴的距离等于1.
②如图3,设直线PQ的解析式为y=kx+b,由,得
解得
∴直线的解析式为,
设,
∴,
所以.
所以.
将点代入,
得.
整理,得.
因式分解,得.
解得,或(与点P重合,舍去).
当时,.
所以点C的坐标是.
九年级数学试题
第I卷(选择题 30分)
选择题(下列各题的四个选项中,只有一项符合题目要求。每题3分,共30分)
1.列图形中,是中心对称图形的有
A.4个 B.3个 C.2个 D.1个
2.一个游戏转盘如图所示,甲、乙、丙、丁四个扇形的圆心角度数分别为,,,.转动转盘,当其停止转动后,指针落在哪个区域的可能性最大
A.甲扇形 B.乙扇形 C.丙扇形 D.丁扇形
(2题图) (3题图)
3.小明用若干个相同的小正方体搭成的一个几何体的三视图如图所示,由此可知,搭成这个几何体的小正方体最多有
A.13个 B.12个 C.11个 D.10个
4.要使方程是关于x的一元二次方程,则
A.a≠0 B.a≠3
C.a≠1且b≠﹣1 D.a≠3且b≠﹣1且c≠0
5.关于的函数的图象与轴有四个不同的公共点,则的取值范围是
A.且 B.
C. D.
6.二次函数y=x2+2bx+4c的图象与x轴的两个交点的横坐标分别为x1,x2,且x1>1,x2-x1=4,当1≤x≤3时,该函数的最小值为m,则m与b,c的数量关系是
A.m=1+2b+4c B.m=4+4b+4c
C.m=9+6b+4c D.m=-b2+4c
7.如图,为⊙O的直径,,,则的长度为
A. B. C. D.
(7题图) (8题图) (9题图)
8.如图,的三个顶点分别为,,.若函数在第一象限内的图象与有交点,则的取值范围是
A. B.
C. D.
9.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,则=
A. B. C. D.
10.如图,四边形ABCD是正方形,过点A,B的圆O与射线AD交于点E,过点C的直径与射线AD交于点F,若,则tan∠CFD等于
或 B.或
C.或 D.2或
第II卷(非选择题 70分)
填空题(每空3分,共15分)
11.随着国家“惠民政策”的陆续出台,为了切实让老百姓得到实惠,某种药品原价198元/瓶,经过连续两次降价后,现仅售78元/瓶,假定两次降价的百分率相同,设该种药品平均每次降价的百分率为x,则列出的关于x方程为 .
12.如图,平行于轴的直线分別交函数与的图象于、两点,过点作轴的平行线交的图象于点,直线DEAC,交的图象于点,则_____.
(12题图) (13题图)
13.如图,反比例函数y=(k>0)在第一象限的图象过点A(1,3),点B(点B在点A的右边),连接AB,AC与BC分别平行x轴、y轴,△ABC的面积为,则点C的坐标为__________.
14.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=6m,AB=1.2m,CO=1m,则栏杆C端应下降的垂直距离CD为____________m.
(14题图) (15题图)
15.某地进行广场修建时,遇到了一个池塘,为了测量池塘隔开的A,B两点之间的距离.根据实际情况,作出如图所示的图形,其中,,AF交BE于D,点C在BD上,有四位技术人员分别测量出以下四组数据:①BC,;②DE,DC,BC;③CD,,;④EF、DE、BD.根据所测数据,能求出A、B间的距离的有___________.(填上所有能求出A、B间距离的序号)
解答题(共55分)
16.(6分)(1)计算:
(2)解方程:
17.(6分)在一个不透明的布袋中放有三个分别标有数,,的乒乓球,它们的质地都相同.现从中任意摸出一个球记下所标的数字,将其放回袋中搅匀,再从袋子里任意摸出一个球记下所标的数字.
(1)请用画树状图法或列表法表示出所有可能的结果.
(2)求两次记下的数字的乘积为正数的概率.
18.(7分)如图,在平面直角坐标系中,已知的三个顶点的坐标分别为、、.
(1)与关于原点成中心对称,写出点、、的坐标;
(2)将绕点顺时针旋转得到,画出;
(3)求的面积.
19.(8分)如图,点在线段上,在的同侧作等腰和等腰,与、分别交于点、.
求证:(1);
(2).
20.(8分)如图,点O在△ABC的BC边上,⊙O经过点A、C,且与BC相交于点D.点E是下半圆弧的中点,连接AE交BC于点F,已知AB=BF.
(1)求证:AB是⊙O的切线;
(2)若OC=3,OF=1,求cos∠B的值.
21.(9分)如图,一次函数与反比例函数的图象交于,两点.
(1)求反比例函数的解析式和的值;
(2)根据图象直接写出不等式的的取值范围;
(3)求的面积.
22.(11分)已知抛物线过点.
(1)求抛物线的解析式;
(2)点A在直线上且在第一象限内,过A作轴于B,以为斜边在其左侧作等腰直角.
①若A与Q重合,求C到抛物线对称轴的距离;
②若C落在抛物线上,求C的坐标.
【参考答案】
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B D A B B C C A A B
二、填空题(每空3分,共30分)
11.198(1-x)2=78 12. 13.(4,3) 14.0.2 15.①③④
三、解答题(共55分)
16.(1)-5 (2)x=-4或x=-5
17.解:(1)列表如下:
-3 -5
-3
-5
由表格可知,共有种等可能的结果.
(2)由(1)知,共有种等可能的结果,
两次记下的数字的乘积为正数的情况有种,
两次记下的数字的乘积为正数的概率.
18.解:(1)如图,即为所求作,点,,;
(2)如图,即为所求作;
(3)的面积.
19.证明:(1)等腰和等腰,
,,
,,,
,,
,且,
∴
(2)∵
,且
∴,
20.解:(1)证明:连接OA、OE,
∵点E是下半圆弧的中点,OE过O,
∴OE⊥DC,
∴∠FOE=90°,
∴∠E+∠OFE=90°,
∵OA=OE,AB=BF,
∴∠BAF=∠BFA,∠E=∠OAE,
∵∠AFB=∠OFE,
∴∠OAE+∠BAF=90°,
即OA⊥AB,
∵OA为半径,
∴AB是⊙O的切线;
(2)解:设AB=x,则BF=x,OB=x+1,
∵OA=OC=3,
由勾股定理得:OB2=AB2+OA2,
∴(1+x)2=32+x2,
解得:x=4,
∴.
21.解:(1)在的图象上,
,
反比例函数的解析式是.
又∵在的图象上,
;
(2)由图像可知:当或时,;
(3),在函数的图象上,
,
解得:,
则一次函数的解析式是,
设直线与轴相交于点,则的坐标是.
∴
.
22.解:(1)将两点分别代入,得
解得.
所以抛物线的解析式是.
(2)①如图2,抛物线的对称轴是y轴,当点A与点重合时,,
作于H.
∵是等腰直角三角形,
∴和也是等腰直角三角形,
∴,
∴点C到抛物线的对称轴的距离等于1.
②如图3,设直线PQ的解析式为y=kx+b,由,得
解得
∴直线的解析式为,
设,
∴,
所以.
所以.
将点代入,
得.
整理,得.
因式分解,得.
解得,或(与点P重合,舍去).
当时,.
所以点C的坐标是.
同课章节目录
