2021-2022学年高一上学期物理人教版(2019)必修第一册 第四章专题牛顿第二定律 瞬变模型 专项练习
文档属性
| 名称 | 2021-2022学年高一上学期物理人教版(2019)必修第一册 第四章专题牛顿第二定律 瞬变模型 专项练习 |  | |
| 格式 | doc | ||
| 文件大小 | 210.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-28 10:44:27 | ||
图片预览



文档简介
第四章《运动和力的关系》牛顿第二定律 瞬变模型 专项练习
一.单选题(共10小题)
1.彩虹圈是相当于弹簧的塑料玩具,如图所示,一人手拿彩虹圈处于竖直状态,彩虹圈静止且质量不可忽略,当他松开手,对彩虹圈的下落过程以下说法正确的是( )
A.彩虹圈的长度始终不变
B.彩虹圈刚开始下落的很短时间内,其长度减小
C.刚松开手的一瞬间,彩虹圈下端有向下的加速度
D.刚松开手的一瞬间,彩虹圈上端的加速度为零
2.两质量均为m的物块A、B用轻弹簧连接起来用细线悬挂在升降机内,如图所示。当升降机正以大小为a=2m/s2的加速度加速上升时,细线突然断裂,则在细线断裂瞬间,A、B的加速度分别为(取竖直向上为正方向,重力加速度大小g取10m/s2)( )
A.﹣22m/s2,2m/s2 B.﹣12m/s2,2m/s2
C.﹣24m/s2,0 D.﹣2m/s2,2m/s2
3.如图所示,质量为0.5kg的物块A悬挂在弹簧测力计下方,木板B托住物块A使整个装置静止,此时测力计的示数为3.0N,重力加速度g=10m/s2。现使木板B以5m/s2的加速度向下运动,木板B开始运动的瞬间,物块A的加速度为( )
A.0 B.4m/s2 C.5m/s2 D.6m/s2
4.如图所示,将两相同的木块a、b置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用轻细绳固定于墙壁。开始时a、b均静止。弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力fa≠0,b所受摩擦力fb=0,现将右侧细绳剪断,则剪断瞬间( )
A.fa大小不变 B.fa方向改变 C.fb仍然为零 D.fa变为零
5.如图所示,质量均为m的三个物块A、B、C,物块B叠放在A上,物块A与C之间用轻弹簧水平连接,物块A、C与水平地面间的动摩擦因数都为μ,物块B与A之间的动摩擦因数为2μ,在水平拉力F的作用下三个物块相对静止一起向右匀加速运动.某时刻,突然撤去水平拉力F,要使拉力撤去瞬间,物块A和B仍能保持相对静止,则水平拉力应不大于( )(已知重力加速度为g)
A.6μmg B.7μmg C.8μmg D.9μmg
6.如图所示,水平地面上固定一倾角为θ的光滑斜面,斜面顶端固定一轻质弹簧,弹簧另一端与A球相连,三个完全相同的小球A、B、C静止在斜面上,质量均为m,A、B、C间均由一轻质细线连接,弹簧与细线均平行于斜面,A、B间细线被烧断的瞬间(重力加速度为g),下列说法正确的是( )
A.A球的加速度沿斜面向上,大小为3gsinθ
B.B球的加速度沿斜面向下,大小为gsinθ
C.C球的受力情况未变,加速度为0
D.B、C之间绳的弹力大小为mgsinθ
7.如图所示,质量为m的小球与轻质弹簧Ⅰ和水平轻绳Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q,弹簧与竖直方向夹角θ=37°若分别剪断Ⅰ、Ⅱ的瞬间,小球的加速度大小分别为a1和a2,则a1:a2为( )
A.1:1 B.3:4 C.4:3 D.3:5
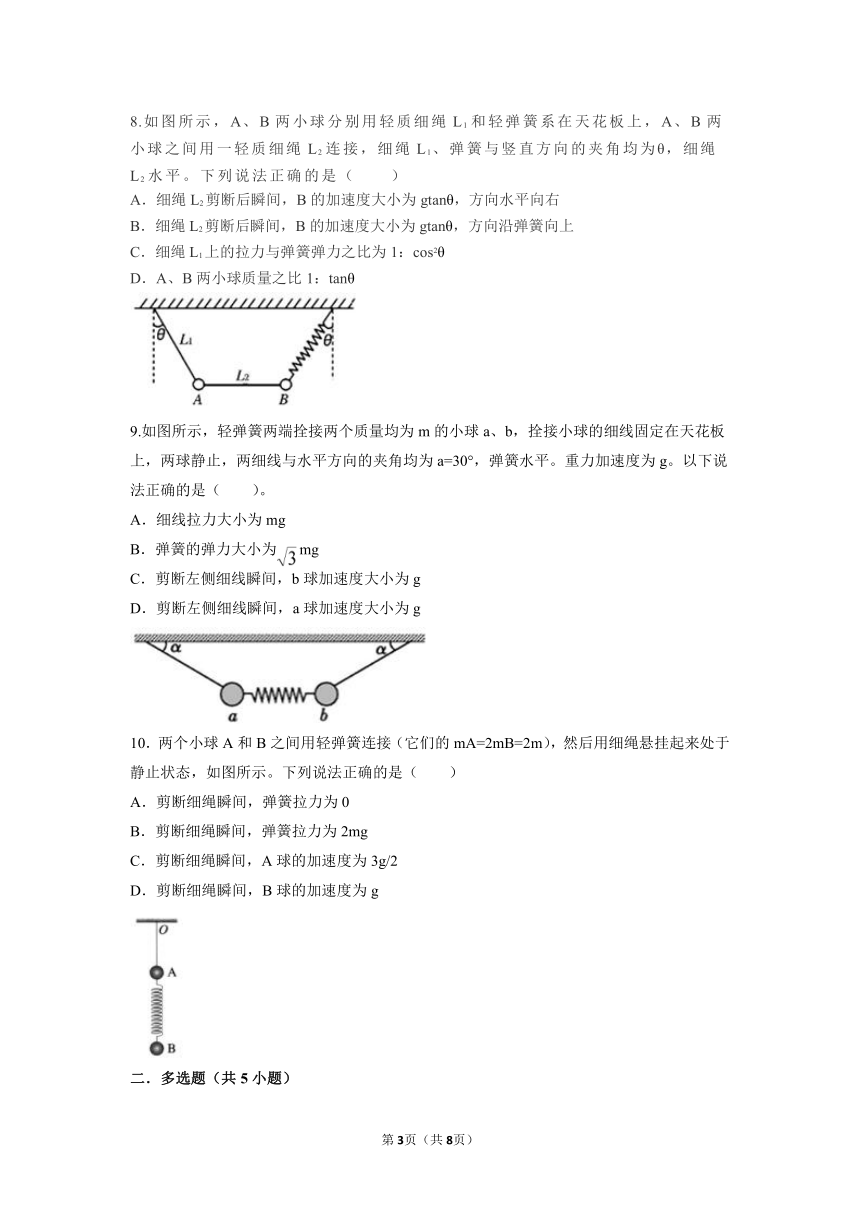
8.如图所示,A、B两小球分别用轻质细绳L1和轻弹簧系在天花板上,A、B两小球之间用一轻质细绳L2连接,细绳L1、弹簧与竖直方向的夹角均为θ,细绳L2水平。下列说法正确的是( )
A.细绳L2剪断后瞬间,B的加速度大小为gtanθ,方向水平向右
B.细绳L2剪断后瞬间,B的加速度大小为gtanθ,方向沿弹簧向上
C.细绳L1上的拉力与弹簧弹力之比为1:cos2θ
D.A、B两小球质量之比1:tanθ
9.如图所示,轻弹簧两端拴接两个质量均为m的小球a、b,拴接小球的细线固定在天花板上,两球静止,两细线与水平方向的夹角均为a=30°,弹簧水平。重力加速度为g。以下说法正确的是( )。
A.细线拉力大小为mg
B.弹簧的弹力大小为 mg
C.剪断左侧细线瞬间,b球加速度大小为g
D.剪断左侧细线瞬间,a球加速度大小为g
10.两个小球A和B之间用轻弹簧连接(它们的mA=2mB=2m),然后用细绳悬挂起来处于静止状态,如图所示。下列说法正确的是( )
A.剪断细绳瞬间,弹簧拉力为0
B.剪断细绳瞬间,弹簧拉力为2mg
C.剪断细绳瞬间,A球的加速度为3g/2
D.剪断细绳瞬间,B球的加速度为g
二.多选题(共5小题)
11.如图所示,A、B两物块用细线相连绕过轻质定滑轮,B和物块C在竖直方向上通过劲度系数为k的轻质弹簧相连,C放在水平地面上。控制A使细线拉直但无弹力。释放A运动至速度最大,此时C恰好离开地面。A始终未落地,滑轮两侧细线始终保持竖直状态。已知B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,则( )
A.C刚离开地面时,B的加速度为零
B.A的质量为2m
C.弹簧恢复原长瞬间,细线中的拉力大小为2mg
D.A的最大速度为
12.在动摩擦因数μ=0.2的水平面上有一个质量为m=2kg的小球,小球与水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳一端相连,如图所示,此时小球处于静止平衡状态,且水平面对小球的弹力恰好为零。取g=10m/s2,以下说法正确的是( )
A.若剪断轻绳,则剪断的瞬间轻弹簧的弹力大小为20N
B.若剪断轻绳,则剪断的瞬间小球的加速度大小为10m/s2,方向向左
C.若剪断弹簧,则剪断的瞬间小球的加速度大小为8m/s2,方向向右
D.若剪断弹簧,则剪断的瞬间小球所受地面的支持力大小、轻绳上的弹力大小、轻弹簧的弹力大小都会突变
13.一根细绳与一根轻弹簧,上端分别固定在A、B两点,下端交于C点共同拉住一个小球,如图所示,AC、BC与竖直方向的夹角均为θ,重力加速度为g,则( )
A.烧断细绳的瞬间,小球的加速度为
B.烧断细绳的瞬间,小球的加速度为gsinθ
C.弹簧在B处断开的瞬间,小球的加速度为gtanθ
D.弹簧在C处与小球断开的瞬间,小球的加速度为gsinθ
14.如图所示,质量M=2kg的水平托盘B与一竖直放置的轻弹簧焊接,托盘上放一质量m=1kg的小物块A,整个装置静止。现对小物块A施加一个竖直向上的变力F,使其从静止开始以加速度a=2m/s2做匀加速直线运动,已知弹簧的劲度系数k=600N/m,g=10m/s2。以下结论正确的是( )
A.变力F的最小值为2N
B.变力F的最小值为6N
C.小物块A与托盘B分离瞬间的速度为0.2m/s
D.小物块A与托盘B分离瞬间的速度为 m/s
15.如图所示,杆Ⅰ的左端固定在P,右端连着质量为m的物体,弹簧Ⅱ右端固定在Q,左端连在物体m上,m静止在光滑水平面上,弹簧的长度比原长大。则对下列情况的叙述正确的是( )
A.剪断Ⅰ的瞬间,Ⅱ对m的弹力立刻消失
B.剪断Ⅰ的瞬间,Ⅱ对m的弹力还存在
C.剪断Ⅱ的瞬间,Ⅰ对m的弹力立即消失
D.剪断Ⅱ的瞬间,Ⅰ对m的弹力还存在
三.填空题(共2小题)
16. 如图所示,A、B两小球用细线连接,C、D两小球用轻弹簧连接,双手分别提起A、C两球,使四个小球均在空中处于静止状态,双手同时释放A、C瞬间(空气阻力不计,重力加速度为g),小球B的加速度大小为 ,小球D的加速度大小为 。
17.如图甲所示,一质量为m的物体系于长度分别为L1、L2的两根细线上,L1的一端悬挂在天花板上,与竖直方向夹角为θ=45°,L2水平拉直,物体处于平衡状态。如图乙所示,将L1换成弹簧后,仍处于平衡状态。现将线L2剪断,则剪断L2的瞬间甲、乙两种情况下物体的加速度之比为 。
通过该题分析总结绳子产生弹力与弹簧产生弹力的特点: 。
四.计算题(共5小题)
18.如图所示,静止在水平面上的A、B两个物体通过一根拉直的轻绳相连,轻绳长度L=0.4m,当其承受拉力增大到Tm=8N时,轻绳瞬间被拉断。已知A的质量m1=2kg,B的质量m2=8kg,A、B与水平面间的动摩擦因数μ=0.2,现用一从零开始逐渐增大的水平力F作用在B上,使A、B向右运动,当F增大到某一值时,轻绳刚好被拉断(g取10m/s2)。
(1)求绳刚被拉断时F的大小;
(2)若绳刚被拉断时,A、B的速度为v=2m/s,保持此时的F大小不变,当A静止时,A、B间的距离为多少?
19.用两根细线a、b和一根轻质弹簧将质量均为m的小球1和2连接,并如图所示悬挂。两小球处于静止状态,细线a与竖直方向的夹角为θ=45°,弹簧水平,重力加速度大小为g。
(1)求细线b对小球1的拉力大小Tb1;
(2)若烧断细线a,求在细线a断开瞬间小球2的加速度大小。
20.如图所示,水平横杆固定,小环A、B套在杆上(其直径略大于杆的直径),用两段不可伸长的轻绳连接小球C,A、B、C构成等边三角形且质量均为m,整个装置处于静止状态,重力加速度用g表示。求:
(1)轻绳AC对C的拉力大小;
(2)A受到的摩擦力的大小;
(3)用手按住A环,突然剪断BC轻绳瞬间,C球的加速度大小。
21.如图,A、B两滑环分别套在间距为d=20cm的水平平行光滑细杆上,A和B的质量分别为1kg、3kg,用一自然长度为20cm的轻弹簧将两环相连,在A环上作用一沿杆向右的小为20N的拉力F,当两环都沿杆以相同的加速度运动时,求:
(1)若突然撤去拉力F,在撤去拉力F的瞬间,A的加速度为多大?方向如何?
(2)若弹簧与杆夹角为53°且仍在弹性限度内,则弹簧的劲度系数k为多少?
22.如图甲所示,倾角为37°的光滑斜面体固定在水平面上,轻弹簧放在斜面上,下端与斜面上的固定挡板相连,处于原长时,上端与斜面上的O点对齐,将质量为m的物块A放在斜面上,并与弹簧上端连接,用力沿斜面向下缓慢推动物块A至C点时,弹簧的压缩量为L,此时由静止释放物块A,物块A沿斜面向上运动到OC中点时速度达到最大,重力加速度为g,不计物块A的大小,弹簧的形变在弹性限度内,斜面足够长,sin37°=0.6,求:
(1)弹簧的劲度系数多大;释放物块A的一瞬间加速度多大;
(2)若用绕过斜面顶端的细线一端连接物块A,另一端吊着物块B,如图乙所示,滑轮与物块A间的细线与斜面平行,将物块A轻推至C点由静止释放,当物块运动到D点时,速度达到最大,DO=L,则物块B的质量多大;物块A的最大速度多大。
第四章《运动和力的关系》牛顿第二定律 瞬变模型 专项练习
参考答案
一.单选题(共10小题)
1.B; 2.A; 3.B; 4.A; 5.A; 6.B; 7.C;8.A;9.B;10.C
二.多选题(共5小题)
11.AB; 12.AD; 13.AD; 14.BC; 15.BC;
三.填空题(共2小题)
16. g,0.
17. 1: ,绳子上力能发生突变,弹簧上力只能渐变。
四.计算题(共5小题)
18.(1)绳刚被拉断时F的大小为40N;
(2)当A静止时,A、B间的距离为2.9m。
19.(1)细线b对小球1的拉力大小Tb1为 mg;
(2)若烧断细线a,在细线a断开瞬间小球2的加速度大小为 g。
20.(1)轻绳AC对C的拉力大小为 mg;
(2)A受到的摩擦力的大小为 mg;
(3)用手按住A环,突然剪断BC轻绳瞬间,C球的加速度大小为 g。
21.(1)若突然撤去拉力F,在撤去拉力F的瞬间,A的加速度为15m/s2,方向水平向左;
(2)若弹簧与杆夹角为53°且仍在弹性限度内,则弹簧的劲度系数k为500N/m。
22.(1)弹簧的劲度系数为 ;释放物块A的一瞬间加速度大小为0.6g;
(2)物块B的质量为 m;物块A的最大速度为 。
第9页(共9页)
一.单选题(共10小题)
1.彩虹圈是相当于弹簧的塑料玩具,如图所示,一人手拿彩虹圈处于竖直状态,彩虹圈静止且质量不可忽略,当他松开手,对彩虹圈的下落过程以下说法正确的是( )
A.彩虹圈的长度始终不变
B.彩虹圈刚开始下落的很短时间内,其长度减小
C.刚松开手的一瞬间,彩虹圈下端有向下的加速度
D.刚松开手的一瞬间,彩虹圈上端的加速度为零
2.两质量均为m的物块A、B用轻弹簧连接起来用细线悬挂在升降机内,如图所示。当升降机正以大小为a=2m/s2的加速度加速上升时,细线突然断裂,则在细线断裂瞬间,A、B的加速度分别为(取竖直向上为正方向,重力加速度大小g取10m/s2)( )
A.﹣22m/s2,2m/s2 B.﹣12m/s2,2m/s2
C.﹣24m/s2,0 D.﹣2m/s2,2m/s2
3.如图所示,质量为0.5kg的物块A悬挂在弹簧测力计下方,木板B托住物块A使整个装置静止,此时测力计的示数为3.0N,重力加速度g=10m/s2。现使木板B以5m/s2的加速度向下运动,木板B开始运动的瞬间,物块A的加速度为( )
A.0 B.4m/s2 C.5m/s2 D.6m/s2
4.如图所示,将两相同的木块a、b置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用轻细绳固定于墙壁。开始时a、b均静止。弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力fa≠0,b所受摩擦力fb=0,现将右侧细绳剪断,则剪断瞬间( )
A.fa大小不变 B.fa方向改变 C.fb仍然为零 D.fa变为零
5.如图所示,质量均为m的三个物块A、B、C,物块B叠放在A上,物块A与C之间用轻弹簧水平连接,物块A、C与水平地面间的动摩擦因数都为μ,物块B与A之间的动摩擦因数为2μ,在水平拉力F的作用下三个物块相对静止一起向右匀加速运动.某时刻,突然撤去水平拉力F,要使拉力撤去瞬间,物块A和B仍能保持相对静止,则水平拉力应不大于( )(已知重力加速度为g)
A.6μmg B.7μmg C.8μmg D.9μmg
6.如图所示,水平地面上固定一倾角为θ的光滑斜面,斜面顶端固定一轻质弹簧,弹簧另一端与A球相连,三个完全相同的小球A、B、C静止在斜面上,质量均为m,A、B、C间均由一轻质细线连接,弹簧与细线均平行于斜面,A、B间细线被烧断的瞬间(重力加速度为g),下列说法正确的是( )
A.A球的加速度沿斜面向上,大小为3gsinθ
B.B球的加速度沿斜面向下,大小为gsinθ
C.C球的受力情况未变,加速度为0
D.B、C之间绳的弹力大小为mgsinθ
7.如图所示,质量为m的小球与轻质弹簧Ⅰ和水平轻绳Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q,弹簧与竖直方向夹角θ=37°若分别剪断Ⅰ、Ⅱ的瞬间,小球的加速度大小分别为a1和a2,则a1:a2为( )
A.1:1 B.3:4 C.4:3 D.3:5
8.如图所示,A、B两小球分别用轻质细绳L1和轻弹簧系在天花板上,A、B两小球之间用一轻质细绳L2连接,细绳L1、弹簧与竖直方向的夹角均为θ,细绳L2水平。下列说法正确的是( )
A.细绳L2剪断后瞬间,B的加速度大小为gtanθ,方向水平向右
B.细绳L2剪断后瞬间,B的加速度大小为gtanθ,方向沿弹簧向上
C.细绳L1上的拉力与弹簧弹力之比为1:cos2θ
D.A、B两小球质量之比1:tanθ
9.如图所示,轻弹簧两端拴接两个质量均为m的小球a、b,拴接小球的细线固定在天花板上,两球静止,两细线与水平方向的夹角均为a=30°,弹簧水平。重力加速度为g。以下说法正确的是( )。
A.细线拉力大小为mg
B.弹簧的弹力大小为 mg
C.剪断左侧细线瞬间,b球加速度大小为g
D.剪断左侧细线瞬间,a球加速度大小为g
10.两个小球A和B之间用轻弹簧连接(它们的mA=2mB=2m),然后用细绳悬挂起来处于静止状态,如图所示。下列说法正确的是( )
A.剪断细绳瞬间,弹簧拉力为0
B.剪断细绳瞬间,弹簧拉力为2mg
C.剪断细绳瞬间,A球的加速度为3g/2
D.剪断细绳瞬间,B球的加速度为g
二.多选题(共5小题)
11.如图所示,A、B两物块用细线相连绕过轻质定滑轮,B和物块C在竖直方向上通过劲度系数为k的轻质弹簧相连,C放在水平地面上。控制A使细线拉直但无弹力。释放A运动至速度最大,此时C恰好离开地面。A始终未落地,滑轮两侧细线始终保持竖直状态。已知B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,则( )
A.C刚离开地面时,B的加速度为零
B.A的质量为2m
C.弹簧恢复原长瞬间,细线中的拉力大小为2mg
D.A的最大速度为
12.在动摩擦因数μ=0.2的水平面上有一个质量为m=2kg的小球,小球与水平轻弹簧及与竖直方向成θ=45°角的不可伸长的轻绳一端相连,如图所示,此时小球处于静止平衡状态,且水平面对小球的弹力恰好为零。取g=10m/s2,以下说法正确的是( )
A.若剪断轻绳,则剪断的瞬间轻弹簧的弹力大小为20N
B.若剪断轻绳,则剪断的瞬间小球的加速度大小为10m/s2,方向向左
C.若剪断弹簧,则剪断的瞬间小球的加速度大小为8m/s2,方向向右
D.若剪断弹簧,则剪断的瞬间小球所受地面的支持力大小、轻绳上的弹力大小、轻弹簧的弹力大小都会突变
13.一根细绳与一根轻弹簧,上端分别固定在A、B两点,下端交于C点共同拉住一个小球,如图所示,AC、BC与竖直方向的夹角均为θ,重力加速度为g,则( )
A.烧断细绳的瞬间,小球的加速度为
B.烧断细绳的瞬间,小球的加速度为gsinθ
C.弹簧在B处断开的瞬间,小球的加速度为gtanθ
D.弹簧在C处与小球断开的瞬间,小球的加速度为gsinθ
14.如图所示,质量M=2kg的水平托盘B与一竖直放置的轻弹簧焊接,托盘上放一质量m=1kg的小物块A,整个装置静止。现对小物块A施加一个竖直向上的变力F,使其从静止开始以加速度a=2m/s2做匀加速直线运动,已知弹簧的劲度系数k=600N/m,g=10m/s2。以下结论正确的是( )
A.变力F的最小值为2N
B.变力F的最小值为6N
C.小物块A与托盘B分离瞬间的速度为0.2m/s
D.小物块A与托盘B分离瞬间的速度为 m/s
15.如图所示,杆Ⅰ的左端固定在P,右端连着质量为m的物体,弹簧Ⅱ右端固定在Q,左端连在物体m上,m静止在光滑水平面上,弹簧的长度比原长大。则对下列情况的叙述正确的是( )
A.剪断Ⅰ的瞬间,Ⅱ对m的弹力立刻消失
B.剪断Ⅰ的瞬间,Ⅱ对m的弹力还存在
C.剪断Ⅱ的瞬间,Ⅰ对m的弹力立即消失
D.剪断Ⅱ的瞬间,Ⅰ对m的弹力还存在
三.填空题(共2小题)
16. 如图所示,A、B两小球用细线连接,C、D两小球用轻弹簧连接,双手分别提起A、C两球,使四个小球均在空中处于静止状态,双手同时释放A、C瞬间(空气阻力不计,重力加速度为g),小球B的加速度大小为 ,小球D的加速度大小为 。
17.如图甲所示,一质量为m的物体系于长度分别为L1、L2的两根细线上,L1的一端悬挂在天花板上,与竖直方向夹角为θ=45°,L2水平拉直,物体处于平衡状态。如图乙所示,将L1换成弹簧后,仍处于平衡状态。现将线L2剪断,则剪断L2的瞬间甲、乙两种情况下物体的加速度之比为 。
通过该题分析总结绳子产生弹力与弹簧产生弹力的特点: 。
四.计算题(共5小题)
18.如图所示,静止在水平面上的A、B两个物体通过一根拉直的轻绳相连,轻绳长度L=0.4m,当其承受拉力增大到Tm=8N时,轻绳瞬间被拉断。已知A的质量m1=2kg,B的质量m2=8kg,A、B与水平面间的动摩擦因数μ=0.2,现用一从零开始逐渐增大的水平力F作用在B上,使A、B向右运动,当F增大到某一值时,轻绳刚好被拉断(g取10m/s2)。
(1)求绳刚被拉断时F的大小;
(2)若绳刚被拉断时,A、B的速度为v=2m/s,保持此时的F大小不变,当A静止时,A、B间的距离为多少?
19.用两根细线a、b和一根轻质弹簧将质量均为m的小球1和2连接,并如图所示悬挂。两小球处于静止状态,细线a与竖直方向的夹角为θ=45°,弹簧水平,重力加速度大小为g。
(1)求细线b对小球1的拉力大小Tb1;
(2)若烧断细线a,求在细线a断开瞬间小球2的加速度大小。
20.如图所示,水平横杆固定,小环A、B套在杆上(其直径略大于杆的直径),用两段不可伸长的轻绳连接小球C,A、B、C构成等边三角形且质量均为m,整个装置处于静止状态,重力加速度用g表示。求:
(1)轻绳AC对C的拉力大小;
(2)A受到的摩擦力的大小;
(3)用手按住A环,突然剪断BC轻绳瞬间,C球的加速度大小。
21.如图,A、B两滑环分别套在间距为d=20cm的水平平行光滑细杆上,A和B的质量分别为1kg、3kg,用一自然长度为20cm的轻弹簧将两环相连,在A环上作用一沿杆向右的小为20N的拉力F,当两环都沿杆以相同的加速度运动时,求:
(1)若突然撤去拉力F,在撤去拉力F的瞬间,A的加速度为多大?方向如何?
(2)若弹簧与杆夹角为53°且仍在弹性限度内,则弹簧的劲度系数k为多少?
22.如图甲所示,倾角为37°的光滑斜面体固定在水平面上,轻弹簧放在斜面上,下端与斜面上的固定挡板相连,处于原长时,上端与斜面上的O点对齐,将质量为m的物块A放在斜面上,并与弹簧上端连接,用力沿斜面向下缓慢推动物块A至C点时,弹簧的压缩量为L,此时由静止释放物块A,物块A沿斜面向上运动到OC中点时速度达到最大,重力加速度为g,不计物块A的大小,弹簧的形变在弹性限度内,斜面足够长,sin37°=0.6,求:
(1)弹簧的劲度系数多大;释放物块A的一瞬间加速度多大;
(2)若用绕过斜面顶端的细线一端连接物块A,另一端吊着物块B,如图乙所示,滑轮与物块A间的细线与斜面平行,将物块A轻推至C点由静止释放,当物块运动到D点时,速度达到最大,DO=L,则物块B的质量多大;物块A的最大速度多大。
第四章《运动和力的关系》牛顿第二定律 瞬变模型 专项练习
参考答案
一.单选题(共10小题)
1.B; 2.A; 3.B; 4.A; 5.A; 6.B; 7.C;8.A;9.B;10.C
二.多选题(共5小题)
11.AB; 12.AD; 13.AD; 14.BC; 15.BC;
三.填空题(共2小题)
16. g,0.
17. 1: ,绳子上力能发生突变,弹簧上力只能渐变。
四.计算题(共5小题)
18.(1)绳刚被拉断时F的大小为40N;
(2)当A静止时,A、B间的距离为2.9m。
19.(1)细线b对小球1的拉力大小Tb1为 mg;
(2)若烧断细线a,在细线a断开瞬间小球2的加速度大小为 g。
20.(1)轻绳AC对C的拉力大小为 mg;
(2)A受到的摩擦力的大小为 mg;
(3)用手按住A环,突然剪断BC轻绳瞬间,C球的加速度大小为 g。
21.(1)若突然撤去拉力F,在撤去拉力F的瞬间,A的加速度为15m/s2,方向水平向左;
(2)若弹簧与杆夹角为53°且仍在弹性限度内,则弹簧的劲度系数k为500N/m。
22.(1)弹簧的劲度系数为 ;释放物块A的一瞬间加速度大小为0.6g;
(2)物块B的质量为 m;物块A的最大速度为 。
第9页(共9页)
