2021-2022学年高一上学期物理人教版(2019)必修第一册-1.2时间 位移 知识点归纳+课堂检测(Word版含答案)
文档属性
| 名称 | 2021-2022学年高一上学期物理人教版(2019)必修第一册-1.2时间 位移 知识点归纳+课堂检测(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 678.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-28 10:49:04 | ||
图片预览




文档简介
1 运动的描述
1.2 时间 位移
一 时间
(1)时刻:指某个时间点。
例如:早上6点50分起床、中午。11点40分放学、新闻联播19点播放。
(2)时间:两个时刻之间的间隔。
例如:新闻联播是30分钟、郑州到上海高铁4个小时、一堂课45分钟。
(3)时间轴:
由于时间具有单向性,是不可逆的所以可以用一个时间轴来表示:
(a)时间轴的五要素:计时起点、正方向、单位间隔、物理量、单位。
(b)时间的表示:
0~2s 2s的时间间隔“前2s3
0~5s 5s的时间间隔“前5s"
0~1s 1s 的时间间隔“第1s 内”
2~3s 1s 的时间间隔“第3秒内”
(c)时刻的表示:
时间轴上的“1s”表示:第2s初或者是第1s 末。
时间轴上的“5s”表示:第5秒末或者是第6秒初。
小结: ns末和(n+1)s初指的是同一时刻。
(4)时间和时刻
时刻表示的是一瞬间,比如物体运动的一瞬间,就好像是一张相片一样,而时间能展示物体运动的过程,就像一段视频一样。
二 位移
路程:质点的实际运动轨迹的长度。
路程只有大小,它常见的单位有米、千米等。
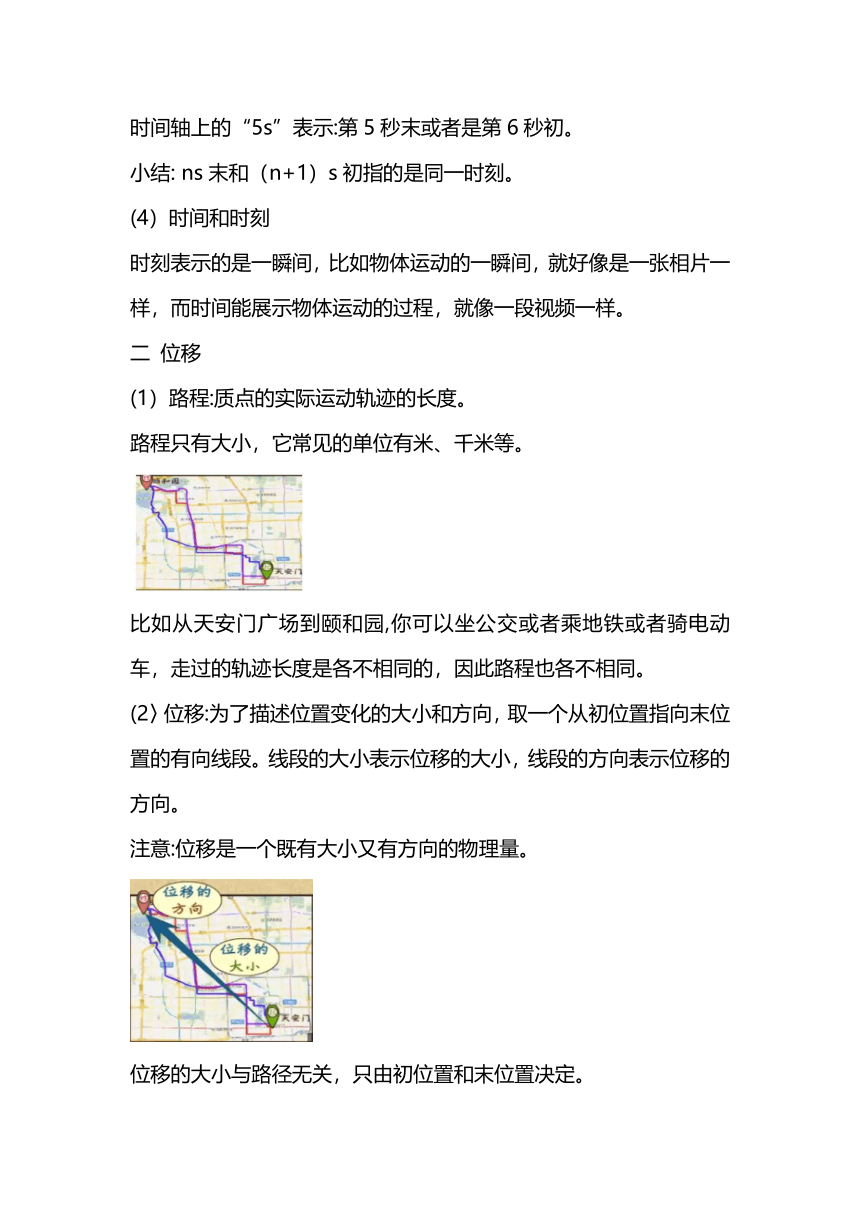
比如从天安门广场到颐和园,你可以坐公交或者乘地铁或者骑电动车,走过的轨迹长度是各不相同的,因此路程也各不相同。
(2〉位移:为了描述位置变化的大小和方向,取一个从初位置指向末位置的有向线段。线段的大小表示位移的大小,线段的方向表示位移的方向。
注意:位移是一个既有大小又有方向的物理量。
位移的大小与路径无关,只由初位置和末位置决定。
位移的大小是否可以等于0呢 答案是肯定的,比如你绕着操场从A点出发跑一圈又回到A点,此时位移的大小就是0。
(4)路程和位移的关系:
①路程的大小是有可能等于位移的大小的,此时物体一定是做单向的
直线运动。
②即使路程的大小有可能等于位移的大小,也不能说路程等于位移,
因为矢量不可能等于标量。路程只有大小,位移不仅有大小还有方向。
(5)位移的正负:
因为位移是个矢量,有方向,并且物体做直线运动时只有两个方向,
故我们可以规定一一个方向为正方向, 与规定的正方向相同的为正,与规定的正方向相反的为负。因此正负号并不代表位移的大小,而是代表了方向。
“知识点”讲解.
知识点:矢量和标量
知识点内容
标量和矢量
1.标量:只有大小没有方向的物理量称之为标量。
如:温度、质量、密度、长度、时间、电阻、各种能量等。
2.标量的计算:遵循代数加减法则。
3.矢量:既有大小,又有方向的物理量,称之为矢量。
如:位移、速度、力等。
4.矢量的表示
用带箭头的有向线段表示:
①箭头方向代表矢量的方向;
②有向线段的长度代表矢量的大小(可以是零,此时方向无意义)。
在表示同一.直线上的矢量时,可以在数值前面加“+”“”号表示方向。加“+”号,表示矢量的方向与规定的正方向相同,加“一”号,表示矢量的方向与规定的正方向相反。
如,规定向右为正方向,上 图所示位移为+6m,下图所示位移为-6m.
5.矢量大小的比较.
矢量大小比较时,只看数值大小,正负只表示方向(矢量的大小没有
负值)。
三 - -维及二维平面求解路程、位移
一维直线运动:
从A运动到B,位移大小的计算公式是: SAB=Xp-XA。 例如A点坐
标是-1,B点坐标是3时,SAB =Xp一XA=3m-(-1m)= 4m。
(2)对于较为复杂的运动,我们可以建立一个一维的坐标轴,画图
进行求解。例如:
小球从10米的高处落下,被地面竖直弹回至5米高度后又下落,被
地面竖直弹回至3米后又下落,被地面弹回至2米后又下落,下落过程中在1米处被接住,求小球的整个过程的路程和位移。
解析:解决此类问题最好是动手画--个坐标轴如下:
路程: S =(10+5X2+3X2+2+1)m=29m.
位移: S=1m- 10m=-9m负号代表 与正方向相反(竖直向下)。
(3)二维平面内的路程、位移求解:
二维平面的路程与位移的求解,--般根据几何关系求出实际路径的长度及两点间直线的长度即可,必要时可以建立二维坐标系。
例如:一个同学向东走8m,再向北走6m,求该同学的路程和位移。
如图所示,我们以出发点为原点,向东为x轴正方向建立直角坐标系,
然后画该同学走过的路径,确定终点的坐标,然后根据几何知识即可知道其走过的路程与发生的位移。
课堂检测
1下面关于时间和时刻的说法不正确的是( )
A3秒初表示时间
B前3秒时间长度是3秒钟
C第n秒时间长度是1秒钟
Dn秒初与n-1秒末是同一个时刻
2下列关于位移和路程的说法,正确的是( )
A位移和路程的大小总相等,但位移是矢量,路程是标量
B位移描述的是直线运动,路程描述的是曲线运动
C位移取决于始、末位置,路程取决于实际运动路径
D运动物体的路程总小于位移
3一人晨跑时,从A出发,其运动轨迹如图所示,其中BC为一半圆,当其到达C点时,则其运动的路程和位移分别为( )
A 500m , 500m
B 500m , 0m
C 500m , 314m
D 614m , 500m
4 关于矢量和标量的说法中正确的是( )
A平均速度、瞬时速度都是矢量,速率、平均速率、时间和质量都是标量
B比较矢量大小,只要比较值的大小,而比较标量的大小要带(+、﹣)符号进行比较
C矢量的合成满足平行四边形法则,标量的合成只要代数加减即可
D矢量和标量没有严格的区别,同一个物理量有时是矢量,有时是标量
5一支队伍长150m,沿着直线做匀速直线运动,由于紧急情况,通讯员从队尾跑步前进300m赶到队首,传达命令后立即返回队尾。
当通讯员从队尾出发再回到队尾的时候,队伍已经前进了200m,则在此过程中通讯员的位移大小为___1___ m,路程为___2___ m.
6 下列说法正确的是( )
A物体的位置对应时间间隔
B研究冰面上花样滑冰运动员的位置时,建立平面直角坐标系
C研究直线运动的位置时,建立直线坐标系
D物体的位移对应时间间隔
7某物体在水平地面上向正南方向运动了20m,然后又向正北方向运动了30m,对于这一过程,下列说法正确的是( )
A物体的位移大小是50m,方向向北
B物体通过的路程是10m
C物体的位移大小是10m,方向向北
D物体的位移大小是10m,方向向南
8学校运动场的弯道可以简化为一个半圆,圆的半径为R=20m,如图所示,某同学从弯道的一端A处沿弯道跑到弯道的另一端B处,该同学的位移大小和路程是( )
A位移大小为40m
B位移大小为62.8m
C路程为40m
D路程为62.8m
参考答案
1第n秒初、n秒初、n秒末、第n秒末都是指时刻,只要出现“初”、“末”字样,表示的就是时刻,A错误;
前3秒指的是0到3之间的线段,长度为3秒钟,B正确;
第n秒指的是n-1到n之间的线段,长度为1秒钟,C正确;
n秒初与n-1秒末是同一个时刻,D正确。
2解:路程没有方向,只有大小,是标量,位移是矢量,位移的方向由初位置指向末位置,路程是标量,是运动路径的长度,路程不是位移的大小.故A错误;
位移和路程都可以描述直线运动和曲线运动,故B错误;
位移的大小等于初位置与末位置之间有向线段的长度,路程是物体运动路线的长度,故C正确.
位移是矢量,路程是标量,位移的大小小于或等于路程,当质点做单向直线运动时,位移的大小一定等于路程.故D错误.
故选:C
3解: 路程等于运动轨迹的长度,为s=πR+300=614m,没有方向,位移大小等于首末位置的距离为x=2R+300=500m,方向从A到C.
故选:D
4解:A、既有大小、又有方向的物理量是矢量.只有大小、没有方向的物理量是标量.可知,平均速度、瞬时速度都是矢量,速率、平均速率、时间和质量都是标量,故A正确.
B、矢量的大小是其绝对值,比较矢量大小,只要比较值的大小,而比较标量的大小要带(+、﹣)符号进行比较,故B正确.
C、矢量的合成遵守平行四边形法则,标量的合成只要代数加减即可,故C正确.
D、矢量和标量是两个完全不同的物理量,一个量不可能既是矢量又是标量.故D错误.
故选:ABC
5解: 人到队前时,队伍前进的距离为s1=300m﹣150m=150m; 人到队尾时,队伍前进的距离是s2=200m﹣150m=50m;
所以人向后跑了s3=150m﹣50m=100m,
因此这个过程中通信兵的路程为:s=s1+s2+s3+s后=150+50+100+100m=400m.
这个过程中通讯兵的位移大小是队伍前进的距离即200m.
故答案为:200;400.
6 解:A、物体的位置对应时刻,A错误;
B、研究冰面上花样滑冰运动员的位置时,建立平面直角坐标系,B正确;
C 研究直线运动的位置时,建立直线坐标系,C正确;
D、物体的位移对应时间间隔,D正确;
故选:BCD。
7 解:物体在水平面上向正南方向运动了20m,然后又向正北方向运动了30m,位移的大小x=30﹣20=10m,方向由南向北,故AD错误;C正确;
路程s=20+30m=50m。故B错误;
故选:C。
8 解:某同学从弯道的一端A处,沿弯道跑到弯道的另一端B处,该同学的位移大小是AB的长度即40m,所有经过的路程是A到B的弧长即62.8m,
故选:AD。
1.2 时间 位移
一 时间
(1)时刻:指某个时间点。
例如:早上6点50分起床、中午。11点40分放学、新闻联播19点播放。
(2)时间:两个时刻之间的间隔。
例如:新闻联播是30分钟、郑州到上海高铁4个小时、一堂课45分钟。
(3)时间轴:
由于时间具有单向性,是不可逆的所以可以用一个时间轴来表示:
(a)时间轴的五要素:计时起点、正方向、单位间隔、物理量、单位。
(b)时间的表示:
0~2s 2s的时间间隔“前2s3
0~5s 5s的时间间隔“前5s"
0~1s 1s 的时间间隔“第1s 内”
2~3s 1s 的时间间隔“第3秒内”
(c)时刻的表示:
时间轴上的“1s”表示:第2s初或者是第1s 末。
时间轴上的“5s”表示:第5秒末或者是第6秒初。
小结: ns末和(n+1)s初指的是同一时刻。
(4)时间和时刻
时刻表示的是一瞬间,比如物体运动的一瞬间,就好像是一张相片一样,而时间能展示物体运动的过程,就像一段视频一样。
二 位移
路程:质点的实际运动轨迹的长度。
路程只有大小,它常见的单位有米、千米等。
比如从天安门广场到颐和园,你可以坐公交或者乘地铁或者骑电动车,走过的轨迹长度是各不相同的,因此路程也各不相同。
(2〉位移:为了描述位置变化的大小和方向,取一个从初位置指向末位置的有向线段。线段的大小表示位移的大小,线段的方向表示位移的方向。
注意:位移是一个既有大小又有方向的物理量。
位移的大小与路径无关,只由初位置和末位置决定。
位移的大小是否可以等于0呢 答案是肯定的,比如你绕着操场从A点出发跑一圈又回到A点,此时位移的大小就是0。
(4)路程和位移的关系:
①路程的大小是有可能等于位移的大小的,此时物体一定是做单向的
直线运动。
②即使路程的大小有可能等于位移的大小,也不能说路程等于位移,
因为矢量不可能等于标量。路程只有大小,位移不仅有大小还有方向。
(5)位移的正负:
因为位移是个矢量,有方向,并且物体做直线运动时只有两个方向,
故我们可以规定一一个方向为正方向, 与规定的正方向相同的为正,与规定的正方向相反的为负。因此正负号并不代表位移的大小,而是代表了方向。
“知识点”讲解.
知识点:矢量和标量
知识点内容
标量和矢量
1.标量:只有大小没有方向的物理量称之为标量。
如:温度、质量、密度、长度、时间、电阻、各种能量等。
2.标量的计算:遵循代数加减法则。
3.矢量:既有大小,又有方向的物理量,称之为矢量。
如:位移、速度、力等。
4.矢量的表示
用带箭头的有向线段表示:
①箭头方向代表矢量的方向;
②有向线段的长度代表矢量的大小(可以是零,此时方向无意义)。
在表示同一.直线上的矢量时,可以在数值前面加“+”“”号表示方向。加“+”号,表示矢量的方向与规定的正方向相同,加“一”号,表示矢量的方向与规定的正方向相反。
如,规定向右为正方向,上 图所示位移为+6m,下图所示位移为-6m.
5.矢量大小的比较.
矢量大小比较时,只看数值大小,正负只表示方向(矢量的大小没有
负值)。
三 - -维及二维平面求解路程、位移
一维直线运动:
从A运动到B,位移大小的计算公式是: SAB=Xp-XA。 例如A点坐
标是-1,B点坐标是3时,SAB =Xp一XA=3m-(-1m)= 4m。
(2)对于较为复杂的运动,我们可以建立一个一维的坐标轴,画图
进行求解。例如:
小球从10米的高处落下,被地面竖直弹回至5米高度后又下落,被
地面竖直弹回至3米后又下落,被地面弹回至2米后又下落,下落过程中在1米处被接住,求小球的整个过程的路程和位移。
解析:解决此类问题最好是动手画--个坐标轴如下:
路程: S =(10+5X2+3X2+2+1)m=29m.
位移: S=1m- 10m=-9m负号代表 与正方向相反(竖直向下)。
(3)二维平面内的路程、位移求解:
二维平面的路程与位移的求解,--般根据几何关系求出实际路径的长度及两点间直线的长度即可,必要时可以建立二维坐标系。
例如:一个同学向东走8m,再向北走6m,求该同学的路程和位移。
如图所示,我们以出发点为原点,向东为x轴正方向建立直角坐标系,
然后画该同学走过的路径,确定终点的坐标,然后根据几何知识即可知道其走过的路程与发生的位移。
课堂检测
1下面关于时间和时刻的说法不正确的是( )
A3秒初表示时间
B前3秒时间长度是3秒钟
C第n秒时间长度是1秒钟
Dn秒初与n-1秒末是同一个时刻
2下列关于位移和路程的说法,正确的是( )
A位移和路程的大小总相等,但位移是矢量,路程是标量
B位移描述的是直线运动,路程描述的是曲线运动
C位移取决于始、末位置,路程取决于实际运动路径
D运动物体的路程总小于位移
3一人晨跑时,从A出发,其运动轨迹如图所示,其中BC为一半圆,当其到达C点时,则其运动的路程和位移分别为( )
A 500m , 500m
B 500m , 0m
C 500m , 314m
D 614m , 500m
4 关于矢量和标量的说法中正确的是( )
A平均速度、瞬时速度都是矢量,速率、平均速率、时间和质量都是标量
B比较矢量大小,只要比较值的大小,而比较标量的大小要带(+、﹣)符号进行比较
C矢量的合成满足平行四边形法则,标量的合成只要代数加减即可
D矢量和标量没有严格的区别,同一个物理量有时是矢量,有时是标量
5一支队伍长150m,沿着直线做匀速直线运动,由于紧急情况,通讯员从队尾跑步前进300m赶到队首,传达命令后立即返回队尾。
当通讯员从队尾出发再回到队尾的时候,队伍已经前进了200m,则在此过程中通讯员的位移大小为___1___ m,路程为___2___ m.
6 下列说法正确的是( )
A物体的位置对应时间间隔
B研究冰面上花样滑冰运动员的位置时,建立平面直角坐标系
C研究直线运动的位置时,建立直线坐标系
D物体的位移对应时间间隔
7某物体在水平地面上向正南方向运动了20m,然后又向正北方向运动了30m,对于这一过程,下列说法正确的是( )
A物体的位移大小是50m,方向向北
B物体通过的路程是10m
C物体的位移大小是10m,方向向北
D物体的位移大小是10m,方向向南
8学校运动场的弯道可以简化为一个半圆,圆的半径为R=20m,如图所示,某同学从弯道的一端A处沿弯道跑到弯道的另一端B处,该同学的位移大小和路程是( )
A位移大小为40m
B位移大小为62.8m
C路程为40m
D路程为62.8m
参考答案
1第n秒初、n秒初、n秒末、第n秒末都是指时刻,只要出现“初”、“末”字样,表示的就是时刻,A错误;
前3秒指的是0到3之间的线段,长度为3秒钟,B正确;
第n秒指的是n-1到n之间的线段,长度为1秒钟,C正确;
n秒初与n-1秒末是同一个时刻,D正确。
2解:路程没有方向,只有大小,是标量,位移是矢量,位移的方向由初位置指向末位置,路程是标量,是运动路径的长度,路程不是位移的大小.故A错误;
位移和路程都可以描述直线运动和曲线运动,故B错误;
位移的大小等于初位置与末位置之间有向线段的长度,路程是物体运动路线的长度,故C正确.
位移是矢量,路程是标量,位移的大小小于或等于路程,当质点做单向直线运动时,位移的大小一定等于路程.故D错误.
故选:C
3解: 路程等于运动轨迹的长度,为s=πR+300=614m,没有方向,位移大小等于首末位置的距离为x=2R+300=500m,方向从A到C.
故选:D
4解:A、既有大小、又有方向的物理量是矢量.只有大小、没有方向的物理量是标量.可知,平均速度、瞬时速度都是矢量,速率、平均速率、时间和质量都是标量,故A正确.
B、矢量的大小是其绝对值,比较矢量大小,只要比较值的大小,而比较标量的大小要带(+、﹣)符号进行比较,故B正确.
C、矢量的合成遵守平行四边形法则,标量的合成只要代数加减即可,故C正确.
D、矢量和标量是两个完全不同的物理量,一个量不可能既是矢量又是标量.故D错误.
故选:ABC
5解: 人到队前时,队伍前进的距离为s1=300m﹣150m=150m; 人到队尾时,队伍前进的距离是s2=200m﹣150m=50m;
所以人向后跑了s3=150m﹣50m=100m,
因此这个过程中通信兵的路程为:s=s1+s2+s3+s后=150+50+100+100m=400m.
这个过程中通讯兵的位移大小是队伍前进的距离即200m.
故答案为:200;400.
6 解:A、物体的位置对应时刻,A错误;
B、研究冰面上花样滑冰运动员的位置时,建立平面直角坐标系,B正确;
C 研究直线运动的位置时,建立直线坐标系,C正确;
D、物体的位移对应时间间隔,D正确;
故选:BCD。
7 解:物体在水平面上向正南方向运动了20m,然后又向正北方向运动了30m,位移的大小x=30﹣20=10m,方向由南向北,故AD错误;C正确;
路程s=20+30m=50m。故B错误;
故选:C。
8 解:某同学从弯道的一端A处,沿弯道跑到弯道的另一端B处,该同学的位移大小是AB的长度即40m,所有经过的路程是A到B的弧长即62.8m,
故选:AD。
