湖北省黄州区一中2013届高三10月考试数学理试题
文档属性
| 名称 | 湖北省黄州区一中2013届高三10月考试数学理试题 | 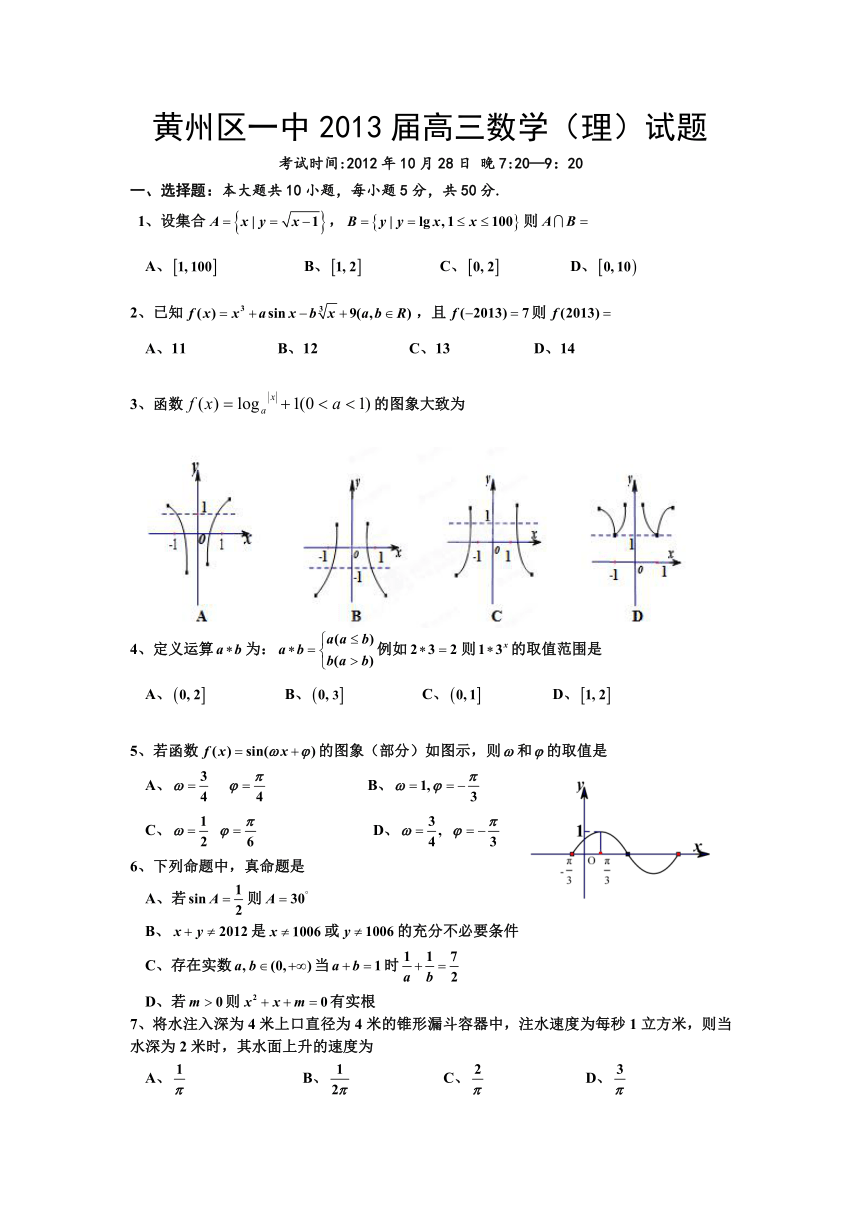 | |
| 格式 | zip | ||
| 文件大小 | 233.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-31 07:48:56 | ||
图片预览



文档简介
黄州区一中2013届高三数学(理)试题
考试时间:2012年10月28日 晚7:20—9:20
一、选择题:本大题共10小题,每小题5分,共50分.
1、设集合,则
A、 B、 C、 D、
2、已知,且则
A、11 B、12 C、13 D、14
3、函数的图象大致为
4、定义运算为:例如则的取值范围是
A、 B、 C、 D、
5、若函数的图象(部分)如图示,则和的取值是
A、 B、
C、 D、
6、下列命题中,真命题是
A、若则
B、是或的充分不必要条件
C、存在实数当时
D、若则有实根
7、将水注入深为4米上口直径为4米的锥形漏斗容器中,注水速度为每秒1立方米,则当水深为2米时,其水面上升的速度为
A、 B、 C、 D、
8、已知圆的半径为3,直径上一点使,为另一直径的两个端点,则
A. B. C. D.
9、已知函数定义在R上的奇函数,当时,,给出下列命题:
①当时, ②函数有2个零点
③的解集为 ④,都有
其中正确命题个数是:
A、1 B、2 C、3 D、4
10、定义在R上的函数若关于x的方程有三个不同的实数解,,,且,则下列结论错误的是
A、 B、 C、 D、
二、填空题:本大题共5小题,每小题5分,共25分.
11、 .
12、集合对于集合A中任何一个元素(x, y)法则f使得
(x, y)与对应,在法则f作用下集合A的象的集合是 .
13、已知,且,则的值为 .
14、若函数在上有最小值,则实数m的取值范围是 .
15、已知集合,则下列命题:
①若则 ②若则
③若则的图象关于原点对称
④若,则对任意不等的实数,总有
⑤若则对任意的实数,部有
其中是正确的命题有 (写出所有正确命题的编号)
三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16、(本小题满分12分)已知向量,其中a、b、c分别是的三内角A、B、C的对边长.
(1)求的值;
(2)求的最大值.
17、(本小题满分12分)设有两个命题:
命题p:不等式对一切实数x都成立;
命题q:已知函数的图象在点处的切线恰好与直线平行,且在上单调递减.
若命题p或q为真,求实数a的取值范围.
18、(本小题满分12分)已知向量且与满足关系式:.
(1)用k表示;
(2)证明:与不垂直;
(3)当与的夹角为时,求k的值.
19、(本小题满分12分)某公司生产一种产品的固定成本是10000元,每生产一件产品需要另外投入80元,又知市场对这种产品的年需求量为800件,且销售收入函数,其中t是产品售出的数量,且(利润=销售收入成本).
(1)若x为年产量,y表示利润,求的解析式;
(2)当年产量为多少时,求工厂年利润的最大值?
20、(本小题满分13分)设的定义域为,值域为,
(1)求证:;
(2)求a的取值范围.
21、(本小题满分14分)
已知函数在[1,+∞)上为增函数,且,,∈R.
(1)求θ的值;
(2)若在[1,+∞)上为单调函数,求m的取值范围;
(3)设,若在[1,e]上至少存在一个,使得成立,
求的取值范围.
数学(理科)试题参考答案及评分细则
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
C
C
A
B
A
C
B
D
二、填空题
11、16 12、 13、 14、 15、②③
三、解答题
18、解:(1)
即
故……(4分)
(2)证明:时,仅当k=2时取=)……(8分)
(3)当与的夹角为时
又
故k=1……(12分)
20、解:(1)证明 :
则
又
……(6分)
(2)
又
则函数上单调递增
上单调递减
即方程有大于2的相异两根……(8分)
即有大于2的相异两根
令
则……(13分)
21. 解:(1)由题意,≥0在上恒成立,即.
∵θ∈(0,π),∴.故在上恒成立,
只须,即,只有.结合θ∈(0,π),得.
(2)由(1),得..
∵在其定义域内为单调函数,
∴或者在[1,+∞)恒成立.
等价于,即,
而 ,()max=1,∴.
等价于,即在[1,+∞)恒成立,
而∈(0,1],.
综上,m的取值范围是.
(3)构造,.
当时,,,,所以在[1,e]上不存在一个使得成立.
当时,.
因为,所以,,所以在恒成立.
故在上单调递增,,只要,
解得
故的取值范围是.
考试时间:2012年10月28日 晚7:20—9:20
一、选择题:本大题共10小题,每小题5分,共50分.
1、设集合,则
A、 B、 C、 D、
2、已知,且则
A、11 B、12 C、13 D、14
3、函数的图象大致为
4、定义运算为:例如则的取值范围是
A、 B、 C、 D、
5、若函数的图象(部分)如图示,则和的取值是
A、 B、
C、 D、
6、下列命题中,真命题是
A、若则
B、是或的充分不必要条件
C、存在实数当时
D、若则有实根
7、将水注入深为4米上口直径为4米的锥形漏斗容器中,注水速度为每秒1立方米,则当水深为2米时,其水面上升的速度为
A、 B、 C、 D、
8、已知圆的半径为3,直径上一点使,为另一直径的两个端点,则
A. B. C. D.
9、已知函数定义在R上的奇函数,当时,,给出下列命题:
①当时, ②函数有2个零点
③的解集为 ④,都有
其中正确命题个数是:
A、1 B、2 C、3 D、4
10、定义在R上的函数若关于x的方程有三个不同的实数解,,,且,则下列结论错误的是
A、 B、 C、 D、
二、填空题:本大题共5小题,每小题5分,共25分.
11、 .
12、集合对于集合A中任何一个元素(x, y)法则f使得
(x, y)与对应,在法则f作用下集合A的象的集合是 .
13、已知,且,则的值为 .
14、若函数在上有最小值,则实数m的取值范围是 .
15、已知集合,则下列命题:
①若则 ②若则
③若则的图象关于原点对称
④若,则对任意不等的实数,总有
⑤若则对任意的实数,部有
其中是正确的命题有 (写出所有正确命题的编号)
三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16、(本小题满分12分)已知向量,其中a、b、c分别是的三内角A、B、C的对边长.
(1)求的值;
(2)求的最大值.
17、(本小题满分12分)设有两个命题:
命题p:不等式对一切实数x都成立;
命题q:已知函数的图象在点处的切线恰好与直线平行,且在上单调递减.
若命题p或q为真,求实数a的取值范围.
18、(本小题满分12分)已知向量且与满足关系式:.
(1)用k表示;
(2)证明:与不垂直;
(3)当与的夹角为时,求k的值.
19、(本小题满分12分)某公司生产一种产品的固定成本是10000元,每生产一件产品需要另外投入80元,又知市场对这种产品的年需求量为800件,且销售收入函数,其中t是产品售出的数量,且(利润=销售收入成本).
(1)若x为年产量,y表示利润,求的解析式;
(2)当年产量为多少时,求工厂年利润的最大值?
20、(本小题满分13分)设的定义域为,值域为,
(1)求证:;
(2)求a的取值范围.
21、(本小题满分14分)
已知函数在[1,+∞)上为增函数,且,,∈R.
(1)求θ的值;
(2)若在[1,+∞)上为单调函数,求m的取值范围;
(3)设,若在[1,e]上至少存在一个,使得成立,
求的取值范围.
数学(理科)试题参考答案及评分细则
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
C
C
A
B
A
C
B
D
二、填空题
11、16 12、 13、 14、 15、②③
三、解答题
18、解:(1)
即
故……(4分)
(2)证明:时,仅当k=2时取=)……(8分)
(3)当与的夹角为时
又
故k=1……(12分)
20、解:(1)证明 :
则
又
……(6分)
(2)
又
则函数上单调递增
上单调递减
即方程有大于2的相异两根……(8分)
即有大于2的相异两根
令
则……(13分)
21. 解:(1)由题意,≥0在上恒成立,即.
∵θ∈(0,π),∴.故在上恒成立,
只须,即,只有.结合θ∈(0,π),得.
(2)由(1),得..
∵在其定义域内为单调函数,
∴或者在[1,+∞)恒成立.
等价于,即,
而 ,()max=1,∴.
等价于,即在[1,+∞)恒成立,
而∈(0,1],.
综上,m的取值范围是.
(3)构造,.
当时,,,,所以在[1,e]上不存在一个使得成立.
当时,.
因为,所以,,所以在恒成立.
故在上单调递增,,只要,
解得
故的取值范围是.
同课章节目录
