人教版九年级数学上册《第二十三章单元综合测试卷》测试题(word版含答案)
文档属性
| 名称 | 人教版九年级数学上册《第二十三章单元综合测试卷》测试题(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 230.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 00:00:00 | ||
图片预览



文档简介
人教版九年级数学上册第二十三章综合测试卷
(时间:90 分钟,满分:100 分)
一、选择题(每小题 4 分,共 32 分)
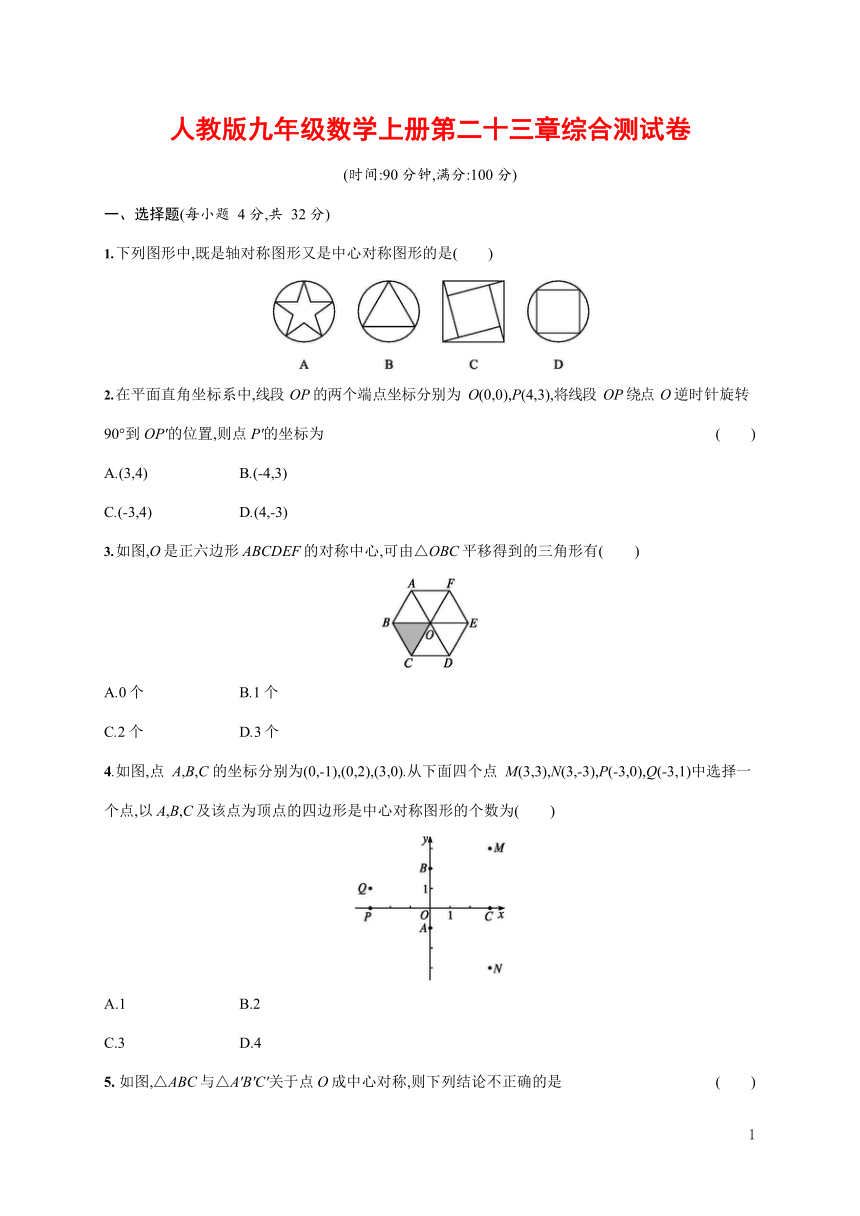
下列图形中,既是轴对称图形又是中心对称图形的是( )
在平面直角坐标系中,线段 OP 的两个端点坐标分别为 O(0,0),P(4,3),将线段 OP 绕点 O 逆时针旋转
90°到 OP'的位置,则点 P'的坐标为 ( )
A.(3,4) B.(-4,3)
C.(-3,4) D.(4,-3)
如图,O 是正六边形 ABCDEF 的对称中心,可由△OBC 平移得到的三角形有( )
A.0 个 B.1 个
C.2 个 D.3 个
4.如图,点 A,B,C 的坐标分别为(0,-1),(0,2),(3,0).从下面四个点 M(3,3),N(3,-3),P(-3,0),Q(-3,1)中选择一
个点,以 A,B,C 及该点为顶点的四边形是中心对称图形的个数为( )
A.1 B.2
C.3 D.4
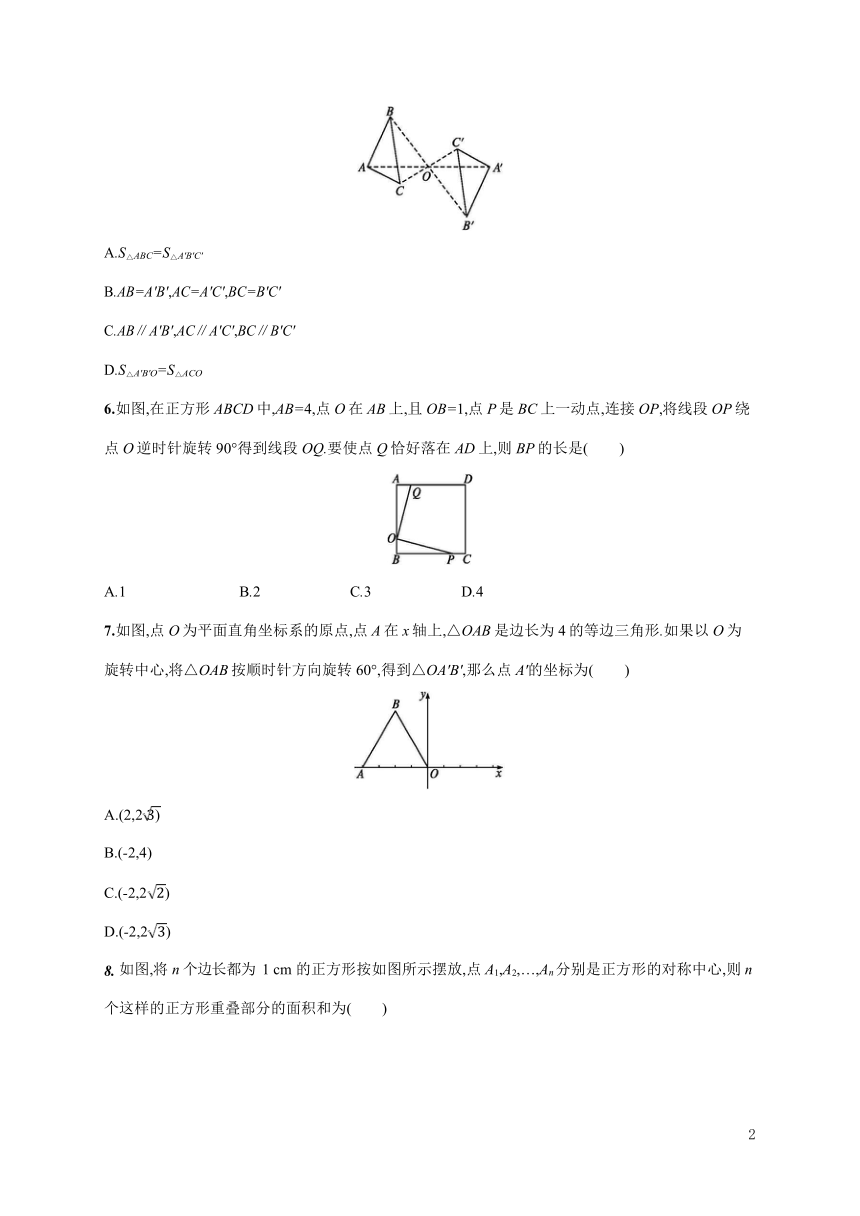
如图,△ABC 与△A'B'C'关于点 O 成中心对称,则下列结论不正确的是 ( )
(
1
)
A.S△ABC=S△A'B'C' B.AB=A'B',AC=A'C',BC=B'C'
C.AB∥A'B',AC∥A'C',BC∥B'C' D.S△A'B'O=S△ACO
如图,在正方形 ABCD 中,AB=4,点 O 在 AB 上,且 OB=1,点 P 是 BC 上一动点,连接 OP,将线段 OP 绕点 O 逆时针旋转 90°得到线段 OQ.要使点 Q 恰好落在 AD 上,则 BP 的长是( )
A.1 B.2 C.3 D.4
如图,点 O 为平面直角坐标系的原点,点 A 在 x 轴上,△OAB 是边长为 4 的等边三角形.如果以 O 为旋转中心,将△OAB 按顺时针方向旋转 60°,得到△OA'B',那么点 A'的坐标为( )
A.(2,2 3)
B.(-2,4)
C.(-2,2 2)
D.(-2,2 3)
如图,将 n 个边长都为 1 cm 的正方形按如图所示摆放,点 A1,A2,…,An 分别是正方形的对称中心,则 n
个这样的正方形重叠部分的面积和为( )
A.1 cm2 B. cm2
4 4
C. -1 cm2 D.
4
(
1
4
)cm2
二、填空题(每小题 5 分,共 20 分)
如图,将△ABC 绕点 C 按顺时针方向旋转至△A'B'C,使点 A'落在 BC 的延长线上.已知∠A=27°,∠
B=40°,则∠ACB'= 度.
一个正方形要绕它的中心至少旋转 度,才能和原来的图形重合.
如图,在△ABC 中,AB=2,BC=3.6,∠B=60°,将△ABC 绕点 A 按顺时针旋转一定的角度得到△ADE, 当点 B 的对应点 D 恰好落在 BC 边上时,CD 的长为 .
如图,将含 30°角的直角三角尺 ABC 绕点 B 顺时针旋转 150°后得到△EBD,连接 CD.若 AB=4 cm,
则△BCD 的面积为 .
三、解答题(共 48 分)
13.(12 分)在平面直角坐标系中,△ABC 三个顶点的坐标分别为 A(2,3),B(1,1),C(5,1).
(1)把△ABC 平移后,其中点 A 移到点 A1(4,5),画出平移后得到的△A1B1C1; (2)把△A1B1C1 绕点 A1 按逆时针方向旋转 90°,画出旋转后的△A2B2C2.
14. (12 分)如图,在菱形 ABCD 中,∠A=110°,点 E 是菱形 ABCD 内一点,连接 CE 绕点 C 顺时针旋转
110°,得到线段 CF,连接 BE,DF,若∠E=86°,求∠F 的度数.
15.(12 分)如图,某实验中学有一块平行四边形的试验田,在试验田的内部有一矩形水池,现在要从水池边上引出一条笔直的水渠,将平行四边形的试验田(包括水池)和矩形水池都平均分成面积相等的两部 分,请你设计一种方案,画出图形,必要时可作简单的说明.
16.(12 分)如图①,有一张矩形纸片,将它沿对角线 AC 剪开,得到△ACD 和△A'BC'.
如图②,将△ACD 沿 A'C'边向上平移,使点 A 与点 C'重合,连接 A'D 和 BC,则四边形 A'BCD 是
形;
如图③,将△ACD 的顶点 A 与点 A'重合,然后绕点 A 沿逆时针方向旋转,使点 D,A,B 在同一条直线上,则旋转角为 度,连接 CC',则四边形 CDBC'是 形;
如图④,将 AC 边与 A'C'边重合,并使顶点 B 和 D 在 AC 边的同一侧,设 AB,CD 相交于点 E,连接 BD,
四边形 ADBC 是什么特殊四边形 请说明你的理由.
参考答案
一、选择题
1.D 2.C 3.C 4.C 5.D 6.C
7.D 旋转后点 A 的对应点 A'与点 B 重合,设 A'B'与 y 轴的交点为 E,从点 A'向 x 轴作垂线,垂足为 F,
如图所示.
根据旋转的性质可知,△A'B'O 也是等边三角形且 OA'=OA=4.
∵∠AOB=60°,∴∠A'OE=30°.
(
2
)∴BE=1OA'=2.
∴OE= '2- 2 = 42-22=2 3.
又四边形 A'FOE 是矩形,
∴A'F=OE=2 3.
∵点 A'位于第二象限,
∴点 A'的坐标为(-2,2 3).故选 D.
8.C 连接正方形的中心和其余两个顶点可证得含 45°角的两个三角形全等,进而求得阴影部分面积
等于正方形面积的1,即是1 cm2.5 个这样的正方形重叠部分(阴影部分)的面积和为 1 × 4 cm2,n 个这
4 4 4
样的正方形重叠部分(阴影部分)的面积和为1×(n-1)= -1(cm2).
4 4
二、填空题
9.46 ∵∠A=27°,∠B=40°,
∴∠ACA'=∠A+∠B=27°+40°=67°.
∵△ABC 绕点 C 按顺时针方向旋转至△A'B'C,∴△ABC≌△A'B'C.
∴∠ACB=∠A'CB'.
∴∠ACB-∠B'CA=∠A'CB'-∠B'CA,
即∠BCB'=∠ACA'.
∴∠BCB'=67°.
∴∠ACB'=180°-∠ACA'-∠BCB'=180°-67°-67°=46°.
10.90
11.1.6 由旋转的特征知 AD=AB.
又因为∠B=60°,所以△ADB 为等边三角形,所以 BD=AB=2,CD=BC-BD=3.6-2=1.6.
12.3 cm2 过点 D 作 BE 的垂线,垂足为 F,由∠ABC=30°及旋转角∠ABE=150°可知∠CBE 为平角.
在 Rt△ABC 中,AB=4 cm,∠ABC=30°,则 AC=2 cm,BC=2 3 cm.由旋转的性质可知 BD=BC=2 3
cm,DE=AC=2 cm,BE=AB=4 cm.由面积法:1DF·BE=1BD·DE,求得 DF= 3 cm.所以△BCD 的面积为
2 2
1BC·DF=1×2 3 × 3=3(cm2).
2 2
三、解答题
解 (1)如图,△A1B1C1 即为所求.
(2)如图,△A2B2C2 即为所求.
解 ∵菱形 ABCD,
∴BC=CD,∠BCD=∠A=110°.
由旋转的性质知,CE=CF.
∵∠ECF=∠BCD=110°,
∴∠BCE=∠DCF=110°-∠DCE.
在△BCE 和△DCF 中,
= ,
∠ = ∠ ,
= ,
∴△BCE≌△DCF,
∴∠F=∠E=86°.
解 如图所示.
因为平行四边形和矩形都是中心对称图形,所以只要过它们的对称中心作一直线即可.
解 (1)因为 AD=AB,AA'=AC,
所以 A'C 与 BD 互相平分.
所以四边形 A'BCD 是平行四边形.故答案为“平行四边”.
因为 DA 垂直于 AB,又知逆时针旋转到点 D,A,B 在同一直线上, 所以旋转角为 90°.
因为∠D=∠B=90°,A,D,B 在同一条直线上, 所以 CD∥BC'.
所以四边形 CDBC'是直角梯形.
故答案为“90 直角梯”.
四边形 ADBC 是等腰梯形. 理由如下:
如图,过点 B 作 BM⊥AC,过点 D 作 DN⊥AC,垂足分别为 M,N,
因为有一张矩形纸片,将它沿对角线 AC 剪开,得到△ACD 和△A'BC', 所以△ACD≌△A'BC'.所以 BM=ND.
所以 BD∥AC.因为 AD=BC,
所以四边形 ADBC 是等腰梯形.
(时间:90 分钟,满分:100 分)
一、选择题(每小题 4 分,共 32 分)
下列图形中,既是轴对称图形又是中心对称图形的是( )
在平面直角坐标系中,线段 OP 的两个端点坐标分别为 O(0,0),P(4,3),将线段 OP 绕点 O 逆时针旋转
90°到 OP'的位置,则点 P'的坐标为 ( )
A.(3,4) B.(-4,3)
C.(-3,4) D.(4,-3)
如图,O 是正六边形 ABCDEF 的对称中心,可由△OBC 平移得到的三角形有( )
A.0 个 B.1 个
C.2 个 D.3 个
4.如图,点 A,B,C 的坐标分别为(0,-1),(0,2),(3,0).从下面四个点 M(3,3),N(3,-3),P(-3,0),Q(-3,1)中选择一
个点,以 A,B,C 及该点为顶点的四边形是中心对称图形的个数为( )
A.1 B.2
C.3 D.4
如图,△ABC 与△A'B'C'关于点 O 成中心对称,则下列结论不正确的是 ( )
(
1
)
A.S△ABC=S△A'B'C' B.AB=A'B',AC=A'C',BC=B'C'
C.AB∥A'B',AC∥A'C',BC∥B'C' D.S△A'B'O=S△ACO
如图,在正方形 ABCD 中,AB=4,点 O 在 AB 上,且 OB=1,点 P 是 BC 上一动点,连接 OP,将线段 OP 绕点 O 逆时针旋转 90°得到线段 OQ.要使点 Q 恰好落在 AD 上,则 BP 的长是( )
A.1 B.2 C.3 D.4
如图,点 O 为平面直角坐标系的原点,点 A 在 x 轴上,△OAB 是边长为 4 的等边三角形.如果以 O 为旋转中心,将△OAB 按顺时针方向旋转 60°,得到△OA'B',那么点 A'的坐标为( )
A.(2,2 3)
B.(-2,4)
C.(-2,2 2)
D.(-2,2 3)
如图,将 n 个边长都为 1 cm 的正方形按如图所示摆放,点 A1,A2,…,An 分别是正方形的对称中心,则 n
个这样的正方形重叠部分的面积和为( )
A.1 cm2 B. cm2
4 4
C. -1 cm2 D.
4
(
1
4
)cm2
二、填空题(每小题 5 分,共 20 分)
如图,将△ABC 绕点 C 按顺时针方向旋转至△A'B'C,使点 A'落在 BC 的延长线上.已知∠A=27°,∠
B=40°,则∠ACB'= 度.
一个正方形要绕它的中心至少旋转 度,才能和原来的图形重合.
如图,在△ABC 中,AB=2,BC=3.6,∠B=60°,将△ABC 绕点 A 按顺时针旋转一定的角度得到△ADE, 当点 B 的对应点 D 恰好落在 BC 边上时,CD 的长为 .
如图,将含 30°角的直角三角尺 ABC 绕点 B 顺时针旋转 150°后得到△EBD,连接 CD.若 AB=4 cm,
则△BCD 的面积为 .
三、解答题(共 48 分)
13.(12 分)在平面直角坐标系中,△ABC 三个顶点的坐标分别为 A(2,3),B(1,1),C(5,1).
(1)把△ABC 平移后,其中点 A 移到点 A1(4,5),画出平移后得到的△A1B1C1; (2)把△A1B1C1 绕点 A1 按逆时针方向旋转 90°,画出旋转后的△A2B2C2.
14. (12 分)如图,在菱形 ABCD 中,∠A=110°,点 E 是菱形 ABCD 内一点,连接 CE 绕点 C 顺时针旋转
110°,得到线段 CF,连接 BE,DF,若∠E=86°,求∠F 的度数.
15.(12 分)如图,某实验中学有一块平行四边形的试验田,在试验田的内部有一矩形水池,现在要从水池边上引出一条笔直的水渠,将平行四边形的试验田(包括水池)和矩形水池都平均分成面积相等的两部 分,请你设计一种方案,画出图形,必要时可作简单的说明.
16.(12 分)如图①,有一张矩形纸片,将它沿对角线 AC 剪开,得到△ACD 和△A'BC'.
如图②,将△ACD 沿 A'C'边向上平移,使点 A 与点 C'重合,连接 A'D 和 BC,则四边形 A'BCD 是
形;
如图③,将△ACD 的顶点 A 与点 A'重合,然后绕点 A 沿逆时针方向旋转,使点 D,A,B 在同一条直线上,则旋转角为 度,连接 CC',则四边形 CDBC'是 形;
如图④,将 AC 边与 A'C'边重合,并使顶点 B 和 D 在 AC 边的同一侧,设 AB,CD 相交于点 E,连接 BD,
四边形 ADBC 是什么特殊四边形 请说明你的理由.
参考答案
一、选择题
1.D 2.C 3.C 4.C 5.D 6.C
7.D 旋转后点 A 的对应点 A'与点 B 重合,设 A'B'与 y 轴的交点为 E,从点 A'向 x 轴作垂线,垂足为 F,
如图所示.
根据旋转的性质可知,△A'B'O 也是等边三角形且 OA'=OA=4.
∵∠AOB=60°,∴∠A'OE=30°.
(
2
)∴BE=1OA'=2.
∴OE= '2- 2 = 42-22=2 3.
又四边形 A'FOE 是矩形,
∴A'F=OE=2 3.
∵点 A'位于第二象限,
∴点 A'的坐标为(-2,2 3).故选 D.
8.C 连接正方形的中心和其余两个顶点可证得含 45°角的两个三角形全等,进而求得阴影部分面积
等于正方形面积的1,即是1 cm2.5 个这样的正方形重叠部分(阴影部分)的面积和为 1 × 4 cm2,n 个这
4 4 4
样的正方形重叠部分(阴影部分)的面积和为1×(n-1)= -1(cm2).
4 4
二、填空题
9.46 ∵∠A=27°,∠B=40°,
∴∠ACA'=∠A+∠B=27°+40°=67°.
∵△ABC 绕点 C 按顺时针方向旋转至△A'B'C,∴△ABC≌△A'B'C.
∴∠ACB=∠A'CB'.
∴∠ACB-∠B'CA=∠A'CB'-∠B'CA,
即∠BCB'=∠ACA'.
∴∠BCB'=67°.
∴∠ACB'=180°-∠ACA'-∠BCB'=180°-67°-67°=46°.
10.90
11.1.6 由旋转的特征知 AD=AB.
又因为∠B=60°,所以△ADB 为等边三角形,所以 BD=AB=2,CD=BC-BD=3.6-2=1.6.
12.3 cm2 过点 D 作 BE 的垂线,垂足为 F,由∠ABC=30°及旋转角∠ABE=150°可知∠CBE 为平角.
在 Rt△ABC 中,AB=4 cm,∠ABC=30°,则 AC=2 cm,BC=2 3 cm.由旋转的性质可知 BD=BC=2 3
cm,DE=AC=2 cm,BE=AB=4 cm.由面积法:1DF·BE=1BD·DE,求得 DF= 3 cm.所以△BCD 的面积为
2 2
1BC·DF=1×2 3 × 3=3(cm2).
2 2
三、解答题
解 (1)如图,△A1B1C1 即为所求.
(2)如图,△A2B2C2 即为所求.
解 ∵菱形 ABCD,
∴BC=CD,∠BCD=∠A=110°.
由旋转的性质知,CE=CF.
∵∠ECF=∠BCD=110°,
∴∠BCE=∠DCF=110°-∠DCE.
在△BCE 和△DCF 中,
= ,
∠ = ∠ ,
= ,
∴△BCE≌△DCF,
∴∠F=∠E=86°.
解 如图所示.
因为平行四边形和矩形都是中心对称图形,所以只要过它们的对称中心作一直线即可.
解 (1)因为 AD=AB,AA'=AC,
所以 A'C 与 BD 互相平分.
所以四边形 A'BCD 是平行四边形.故答案为“平行四边”.
因为 DA 垂直于 AB,又知逆时针旋转到点 D,A,B 在同一直线上, 所以旋转角为 90°.
因为∠D=∠B=90°,A,D,B 在同一条直线上, 所以 CD∥BC'.
所以四边形 CDBC'是直角梯形.
故答案为“90 直角梯”.
四边形 ADBC 是等腰梯形. 理由如下:
如图,过点 B 作 BM⊥AC,过点 D 作 DN⊥AC,垂足分别为 M,N,
因为有一张矩形纸片,将它沿对角线 AC 剪开,得到△ACD 和△A'BC', 所以△ACD≌△A'BC'.所以 BM=ND.
所以 BD∥AC.因为 AD=BC,
所以四边形 ADBC 是等腰梯形.
同课章节目录
