沪科版数学七年级上册 4.3 线段的长短比较教案
文档属性
| 名称 | 沪科版数学七年级上册 4.3 线段的长短比较教案 |  | |
| 格式 | docx | ||
| 文件大小 | 128.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 15:26:15 | ||
图片预览

文档简介
初中数学沪科版七年级上册第四章第三节《线段的长短比较》
4.3 线段的长短比较
教学目标
1.根据实际条件,灵活选用叠合与度量等方法比较线段的长短,能说出线段长短比较的结果,从“数”和“形”两个方面理解线段存在的长短以及线段的和差关系。
2.借助具体情境了解“两点之间的所有连线中,线段最短”的性质,并能运用它解释一些实际现象。
3.了解线段中点的概念和几何语言表示。
教学重点和难点
重点:线段的和差关系和线段的基本性质及其应用。
难点:几何语言的表述。
教学过程
一 情境导入
上一节我们学习了线段、射线、直线,知道线段有两个端点,线段有长度。线段有长度,线段就有长短比较,本节课我们学习线段的长短比较(板书课题)。
二 解读探究
互动1
师:课件展示:黑板边沿和课桌边沿哪个长?白板边沿和黑板边沿哪个长?甲同学和乙同学他俩谁的个子高?你是怎么比较的?
生:黑板边沿长,课桌边沿短。通过目测知道的,因为这两条线段长短差异明显。白板边沿和黑板边沿长度看起来差不多,要用刻度尺测量才能知道谁长谁短。两同学比身高,让他们背靠背,站在同一平地上,谁的头顶高谁的个子就高。
明确:根据实际条件,灵活选用观察、叠合和度量法。
师::课件动画演示:叠合法的操作要点和三种结论。
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB=CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
明确:线段长短比较有三种结果,同时为后面尺规作图做些铺垫。
生:完成课后第1题练习(用圆规、刻度尺都可)。
师:线段有长短,线段之间就存在和差(用粉笔演示:一根长的线段可以看成两根短的线段之和),下面我们学习线段的和差。
互动2
师:课件展示:已知:点C在线段AB的延长线上,如果AB=a,线段BC=b.那么AC与AB,BC之间有何关系
生:线段AC就是AB与BC的和。
师:记作AC=AB+BC=a+b
师:已知:点C在线段AB上,如果AB=a,线段BC=b.那么AC与AB,BC之间有何关系
生:线段AC是AB与BC的差。记作:AC=AB—BC
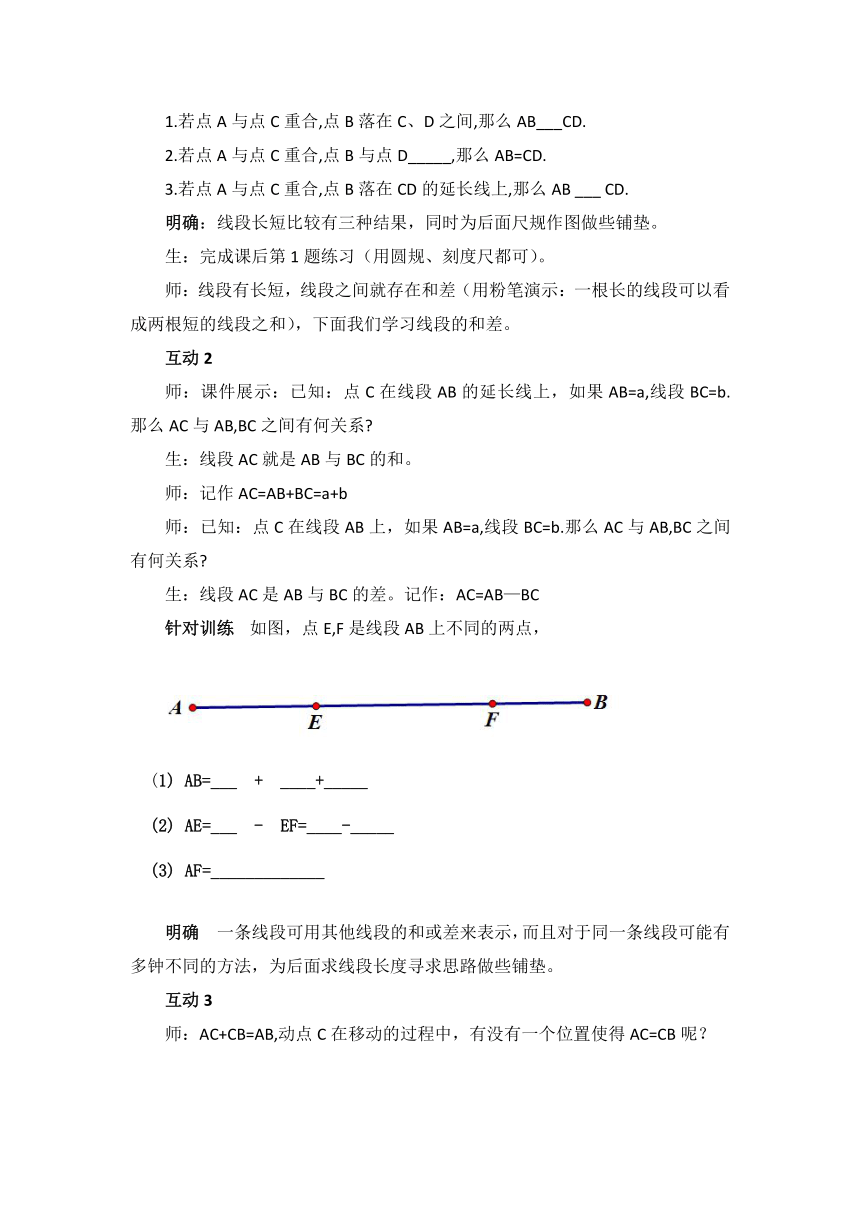
针对训练 如图,点E,F是线段AB上不同的两点,
明确 一条线段可用其他线段的和或差来表示,而且对于同一条线段可能有多钟不同的方法,为后面求线段长度寻求思路做些铺垫。
互动3
师:AC+CB=AB,动点C在移动的过程中,有没有一个位置使得AC=CB呢?
生:线段AB中间位置。
师:点C在线段AB上且使线段AC,CB相等,这样的点C叫做线段AB的中点。
几何语言:AC=CB=AB或AB=AC+CB=2AC=2CB
师:播放线段中点小视频。
互动4
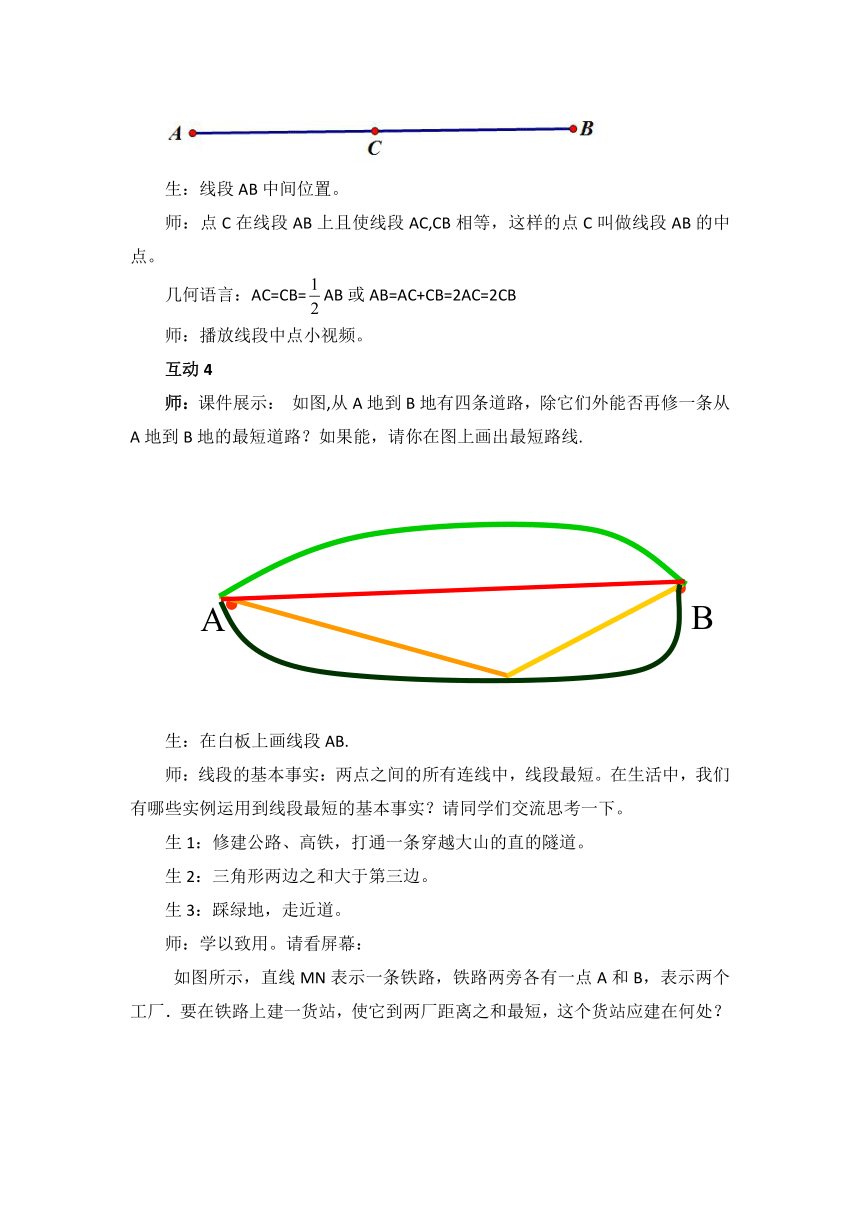
师:课件展示: 如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你在图上画出最短路线.
生:在白板上画线段AB.
师:线段的基本事实:两点之间的所有连线中,线段最短。在生活中,我们有哪些实例运用到线段最短的基本事实?请同学们交流思考一下。
生1:修建公路、高铁,打通一条穿越大山的直的隧道。
生2:三角形两边之和大于第三边。
生3:踩绿地,走近道。
师:学以致用。请看屏幕:
如图所示,直线MN表示一条铁路,铁路两旁各有一点A和B,表示两个工厂.要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?
生:在白板上操作:连接AB交直线MN于点P,则P点为货站。
师:用几何画板动态演示:线段AB最短。
师:两点之间线段的长度,叫做两点之间的距离。
师:线段是最常见,也是最基本的几何图形。下面我们利用线段的和差、线段中点求线段长度。
三 应用迁移
例1 已知:线段AB=4 ,延长AB至点C,使AC=11.点D是AB的中点,点E是AC的中点.求DE的长.
师:与学生一起画图,分析,并给出规范解答。
明确:几何计算题与小学算术有很大区别。有数学图形语言而没有图形的题,解题时要画出与题意相符合的图,再求解.要求每一步有理有据,先写出图形之间的关系,才能代入数据逐段计算。
例2 点A,O,B在一条直线上,线段AO=3,OB=1,C是AO的中点,D是OB的中点.请同学们画出图形,并求线段CD的长.
生1:上黑板画图。
生2:分析思路。
生3:上黑板给出解答。
明确:当三个点在同一条直线上时,要注意讨论第三点是在其余两点确定的线段上,还是在线段的延长线上,即要分类讨论。
例3 如图,B、C 两点把线段AD分成2∶3∶4的三部分,点E是线段AD的中点,EC=2cm,求线段AD的长.
师:提示用方程法,及前面学过的设K法。
解:设AB=2K,则BC=3K,CD=4K,
由线段的和差,得AD=AB+BC+CD=9K.
由E为AD的中点,得ED= AD=K.
由线段的和差,得CE=DE-CD=K -4K= K =2.
解得K=4.
∴AD=9K=36(cm).
明确:在遇到线段之间比的问题时,往往设出未知数,列方程解答简便快捷。.
四 学习小结(生讲完后师归纳)
知识点:
1.比较线段长短的方法
2.线段的和、线段的差
3.线段的中点
4.两点之间,线段最短
5.两点之间的距离
能力点:
1几何画图训练
几何推理语言入门
数形结合、分类讨论、方程思想的渗透
五 当堂检测
1.如图,由AB=CD可得AC与BD的大小关系正确的是( )
A.AC>BD B.AC<BD
C.AC=BD D.不能确定
2.已知M是线段AB的中点,①AB=2AM;②BM=1/2AB;③AM=BM;④AM+BM=AB.上面四个式子中,正确的有( )
A.1个 B.2个 C.3个 D.4个
3.已知线段AB=6 cm,在直线AB上画线段AC=2cm,则BC的长是___________.
4.若AB = 6cm,点C是线段AB的中点,点D是线段CB的中点, 求:线段AD的长是多少
5.如图,从A地到B地有三条路①,②,③可走(图中“┍,“┙”,“┕”表示直角),则第________条路最短,另外两条路的长短关系是________
六 课后作业
习题4.3 第2、3、4共三题。
4.3 线段的长短比较
教学目标
1.根据实际条件,灵活选用叠合与度量等方法比较线段的长短,能说出线段长短比较的结果,从“数”和“形”两个方面理解线段存在的长短以及线段的和差关系。
2.借助具体情境了解“两点之间的所有连线中,线段最短”的性质,并能运用它解释一些实际现象。
3.了解线段中点的概念和几何语言表示。
教学重点和难点
重点:线段的和差关系和线段的基本性质及其应用。
难点:几何语言的表述。
教学过程
一 情境导入
上一节我们学习了线段、射线、直线,知道线段有两个端点,线段有长度。线段有长度,线段就有长短比较,本节课我们学习线段的长短比较(板书课题)。
二 解读探究
互动1
师:课件展示:黑板边沿和课桌边沿哪个长?白板边沿和黑板边沿哪个长?甲同学和乙同学他俩谁的个子高?你是怎么比较的?
生:黑板边沿长,课桌边沿短。通过目测知道的,因为这两条线段长短差异明显。白板边沿和黑板边沿长度看起来差不多,要用刻度尺测量才能知道谁长谁短。两同学比身高,让他们背靠背,站在同一平地上,谁的头顶高谁的个子就高。
明确:根据实际条件,灵活选用观察、叠合和度量法。
师::课件动画演示:叠合法的操作要点和三种结论。
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB=CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
明确:线段长短比较有三种结果,同时为后面尺规作图做些铺垫。
生:完成课后第1题练习(用圆规、刻度尺都可)。
师:线段有长短,线段之间就存在和差(用粉笔演示:一根长的线段可以看成两根短的线段之和),下面我们学习线段的和差。
互动2
师:课件展示:已知:点C在线段AB的延长线上,如果AB=a,线段BC=b.那么AC与AB,BC之间有何关系
生:线段AC就是AB与BC的和。
师:记作AC=AB+BC=a+b
师:已知:点C在线段AB上,如果AB=a,线段BC=b.那么AC与AB,BC之间有何关系
生:线段AC是AB与BC的差。记作:AC=AB—BC
针对训练 如图,点E,F是线段AB上不同的两点,
明确 一条线段可用其他线段的和或差来表示,而且对于同一条线段可能有多钟不同的方法,为后面求线段长度寻求思路做些铺垫。
互动3
师:AC+CB=AB,动点C在移动的过程中,有没有一个位置使得AC=CB呢?
生:线段AB中间位置。
师:点C在线段AB上且使线段AC,CB相等,这样的点C叫做线段AB的中点。
几何语言:AC=CB=AB或AB=AC+CB=2AC=2CB
师:播放线段中点小视频。
互动4
师:课件展示: 如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你在图上画出最短路线.
生:在白板上画线段AB.
师:线段的基本事实:两点之间的所有连线中,线段最短。在生活中,我们有哪些实例运用到线段最短的基本事实?请同学们交流思考一下。
生1:修建公路、高铁,打通一条穿越大山的直的隧道。
生2:三角形两边之和大于第三边。
生3:踩绿地,走近道。
师:学以致用。请看屏幕:
如图所示,直线MN表示一条铁路,铁路两旁各有一点A和B,表示两个工厂.要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?
生:在白板上操作:连接AB交直线MN于点P,则P点为货站。
师:用几何画板动态演示:线段AB最短。
师:两点之间线段的长度,叫做两点之间的距离。
师:线段是最常见,也是最基本的几何图形。下面我们利用线段的和差、线段中点求线段长度。
三 应用迁移
例1 已知:线段AB=4 ,延长AB至点C,使AC=11.点D是AB的中点,点E是AC的中点.求DE的长.
师:与学生一起画图,分析,并给出规范解答。
明确:几何计算题与小学算术有很大区别。有数学图形语言而没有图形的题,解题时要画出与题意相符合的图,再求解.要求每一步有理有据,先写出图形之间的关系,才能代入数据逐段计算。
例2 点A,O,B在一条直线上,线段AO=3,OB=1,C是AO的中点,D是OB的中点.请同学们画出图形,并求线段CD的长.
生1:上黑板画图。
生2:分析思路。
生3:上黑板给出解答。
明确:当三个点在同一条直线上时,要注意讨论第三点是在其余两点确定的线段上,还是在线段的延长线上,即要分类讨论。
例3 如图,B、C 两点把线段AD分成2∶3∶4的三部分,点E是线段AD的中点,EC=2cm,求线段AD的长.
师:提示用方程法,及前面学过的设K法。
解:设AB=2K,则BC=3K,CD=4K,
由线段的和差,得AD=AB+BC+CD=9K.
由E为AD的中点,得ED= AD=K.
由线段的和差,得CE=DE-CD=K -4K= K =2.
解得K=4.
∴AD=9K=36(cm).
明确:在遇到线段之间比的问题时,往往设出未知数,列方程解答简便快捷。.
四 学习小结(生讲完后师归纳)
知识点:
1.比较线段长短的方法
2.线段的和、线段的差
3.线段的中点
4.两点之间,线段最短
5.两点之间的距离
能力点:
1几何画图训练
几何推理语言入门
数形结合、分类讨论、方程思想的渗透
五 当堂检测
1.如图,由AB=CD可得AC与BD的大小关系正确的是( )
A.AC>BD B.AC<BD
C.AC=BD D.不能确定
2.已知M是线段AB的中点,①AB=2AM;②BM=1/2AB;③AM=BM;④AM+BM=AB.上面四个式子中,正确的有( )
A.1个 B.2个 C.3个 D.4个
3.已知线段AB=6 cm,在直线AB上画线段AC=2cm,则BC的长是___________.
4.若AB = 6cm,点C是线段AB的中点,点D是线段CB的中点, 求:线段AD的长是多少
5.如图,从A地到B地有三条路①,②,③可走(图中“┍,“┙”,“┕”表示直角),则第________条路最短,另外两条路的长短关系是________
六 课后作业
习题4.3 第2、3、4共三题。
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
