沪科版数学九年级上册 23.2 解直角三角形教案
文档属性
| 名称 | 沪科版数学九年级上册 23.2 解直角三角形教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 95.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 14:19:23 | ||
图片预览

文档简介
课题:解直角三角形实际应用(复习课)
教学目标:1.理解仰角,俯角,坡度(坡比),坡角,方向角的相关概念.
2.利用数形结合思想,化归思想,方程思想将实际问题中的数量关系转化为直角三角形中元素的关系,进一步提高学生的数学应用意识和解决实际问题的能力.
教学重点:解直角三角形的实际应用.
教学难点:灵活运用直角三角形边角关系解决生活中的实际问题.
教学过程:
引入
展示安徽中考考纲中关于解直角三角形实际应用的相关要求,展示近6年来安徽中考题中解直角三角形的实际应用的分值统计,体现其重要性,引入课题.
(二)复习
一、仰角,俯角,坡度(坡比),坡角,方向角的相关概念.
解直角三角形的实际应用
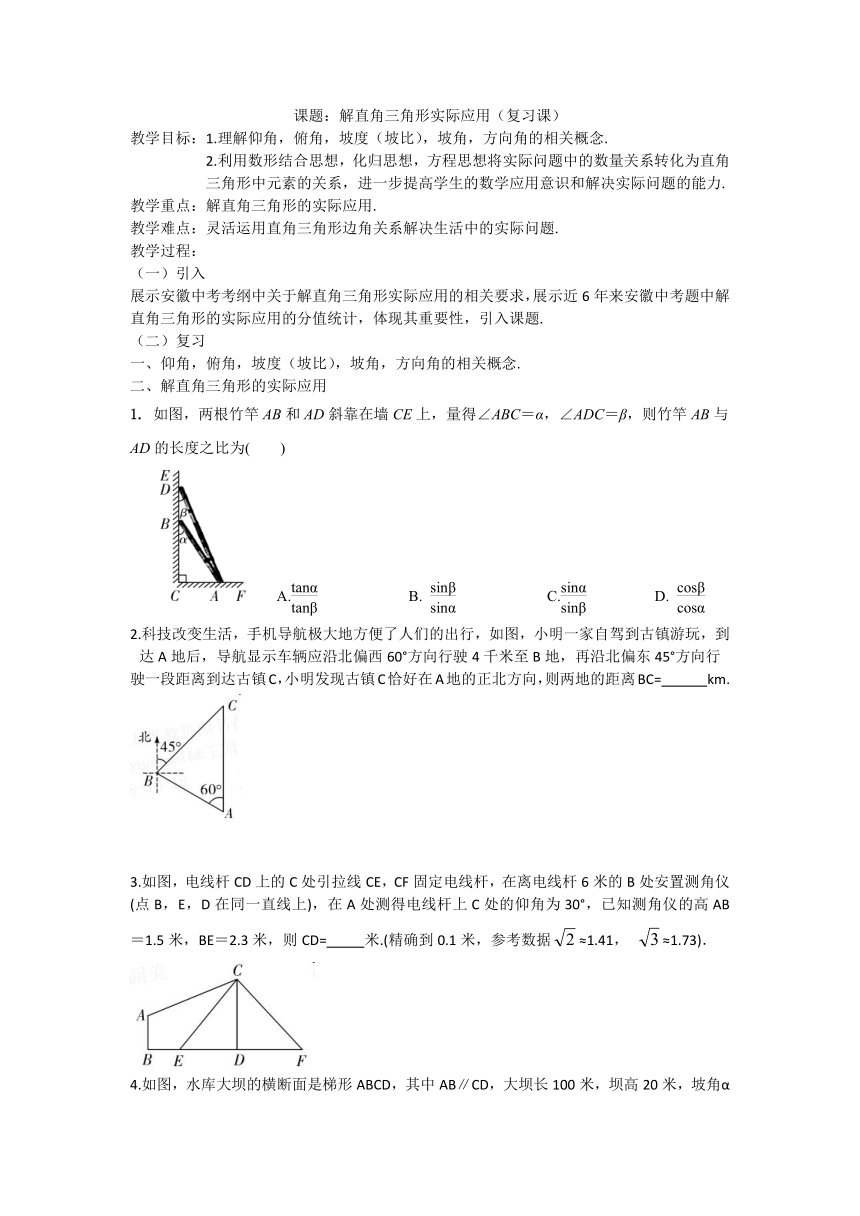
1. 如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为( )
A. B. C. D.
2.科技改变生活,手机导航极大地方便了人们的出行,如图,小明一家自驾到古镇游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4千米至B地,再沿北偏东45°方向行
驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,则两地的距离BC= km.
3.如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,则CD= 米.(精确到0.1米,参考数据≈1.41, ≈1.73).
4.如图,水库大坝的横断面是梯形ABCD,其中AB∥CD,大坝长100米,坝高20米,坡角α=45°,汛期来临前对其进行了加固,改造后的背水面坡度为1∶ ,坝顶面加宽1米,则加固后坝底增加的宽度AF= 米.
5. 如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着仰角为30°的山坡前进1000米到达D处,在D处测得山顶B的仰角为60°,BC⊥AC,求山的高度BC.
课堂小结
添加辅助线
实际问题 解直角三角形问题
构造直角三角形
数形结合思想
数学思想 方程思想
化归思想
课后作业:精练本41,42页
教学反思
解直角三角形的实际应用在中考中都会以解答题的形式出现,分值比重很大,是学生要掌握的重点,该类型的实际应用关键是能将其化归为解直角三角形的问题。对于直接解三角形和解一个直角三角形的类型难度不大,学生能够掌握的很好,难点在于解两个直角三角形。在教学过程中如何构造直角三角形,利用直角三角形中元素的关系来解决实际问题是难点。尤其是四边形和三角形的模型,学生容易出错。
教学目标:1.理解仰角,俯角,坡度(坡比),坡角,方向角的相关概念.
2.利用数形结合思想,化归思想,方程思想将实际问题中的数量关系转化为直角三角形中元素的关系,进一步提高学生的数学应用意识和解决实际问题的能力.
教学重点:解直角三角形的实际应用.
教学难点:灵活运用直角三角形边角关系解决生活中的实际问题.
教学过程:
引入
展示安徽中考考纲中关于解直角三角形实际应用的相关要求,展示近6年来安徽中考题中解直角三角形的实际应用的分值统计,体现其重要性,引入课题.
(二)复习
一、仰角,俯角,坡度(坡比),坡角,方向角的相关概念.
解直角三角形的实际应用
1. 如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为( )
A. B. C. D.
2.科技改变生活,手机导航极大地方便了人们的出行,如图,小明一家自驾到古镇游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4千米至B地,再沿北偏东45°方向行
驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,则两地的距离BC= km.
3.如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,则CD= 米.(精确到0.1米,参考数据≈1.41, ≈1.73).
4.如图,水库大坝的横断面是梯形ABCD,其中AB∥CD,大坝长100米,坝高20米,坡角α=45°,汛期来临前对其进行了加固,改造后的背水面坡度为1∶ ,坝顶面加宽1米,则加固后坝底增加的宽度AF= 米.
5. 如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着仰角为30°的山坡前进1000米到达D处,在D处测得山顶B的仰角为60°,BC⊥AC,求山的高度BC.
课堂小结
添加辅助线
实际问题 解直角三角形问题
构造直角三角形
数形结合思想
数学思想 方程思想
化归思想
课后作业:精练本41,42页
教学反思
解直角三角形的实际应用在中考中都会以解答题的形式出现,分值比重很大,是学生要掌握的重点,该类型的实际应用关键是能将其化归为解直角三角形的问题。对于直接解三角形和解一个直角三角形的类型难度不大,学生能够掌握的很好,难点在于解两个直角三角形。在教学过程中如何构造直角三角形,利用直角三角形中元素的关系来解决实际问题是难点。尤其是四边形和三角形的模型,学生容易出错。
