沪科版数学九年级上册 21.3 二次函数与一元二次方程 课件(共13张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 21.3 二次函数与一元二次方程 课件(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 189.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 14:06:21 | ||
图片预览




文档简介
(共13张PPT)
二次函数与一元二次方程
x
y
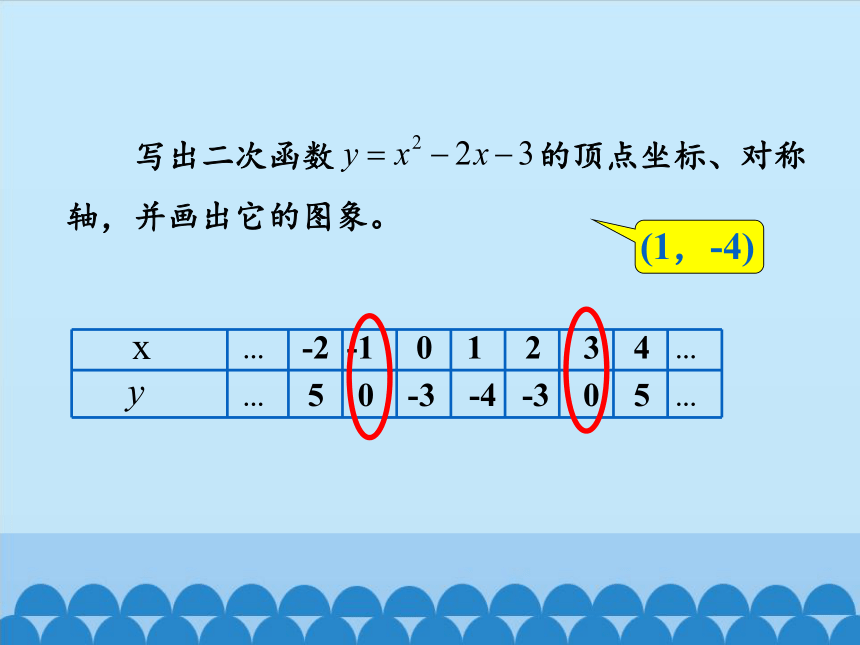
… -2 -1 0 1 2 3 4 …
… 5 0 -3 -4 -3 0 5 …
(1,-4)
写出二次函数 的顶点坐标、对称轴,并画出它的图象。
N
M
当x为何值时,y=0?
x=-1,x=3
探究一
一般地,如果二次函数y=ax2+bx+c的图象与x轴有两个公共点(x1,0)、(x2,0),那么一元二次方程ax2+bx+c=0有两个不相等的实数根x=x1、x=x2,反之亦成立。
不画图象,你能说出函数 的图象与x轴的交点坐标吗?
解:当y=0时,
解得:
所以,函数 的图象与x轴的交点坐标为(-3,0)和(2,0)。
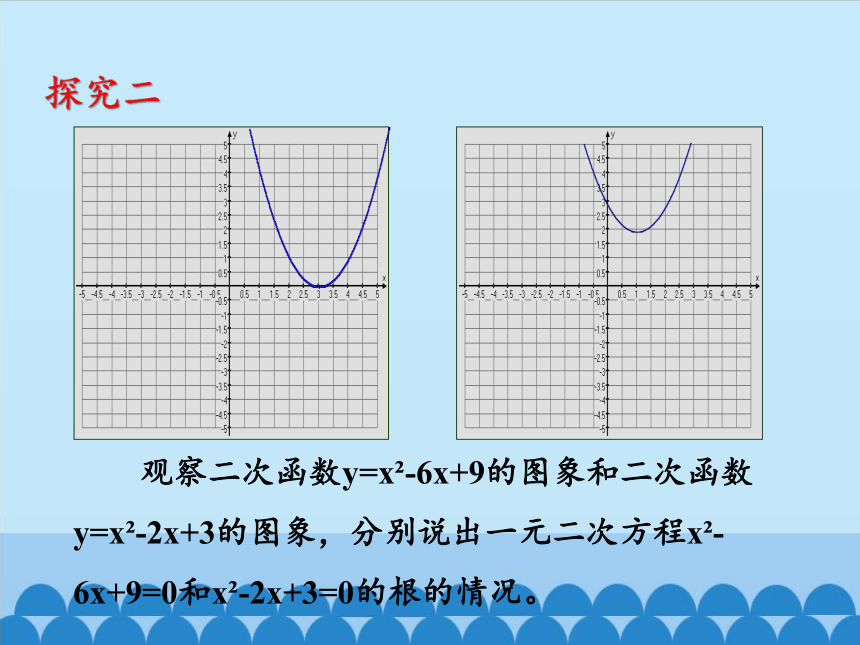
探究二
观察二次函数y=x -6x+9的图象和二次函数y=x -2x+3的图象,分别说出一元二次方程x -6x+9=0和x -2x+3=0的根的情况。
二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0的根的关系?
二次函数y=ax2+bx+c的图象与x轴的交点 一元二次方程ax2+bx+c=0的根 b2-4ac
有两个交点
有两个不相等的实数根
b2-4ac>0
有一个交点
有两个相等的实数根
b2-4ac=0
没有交点
没有实数根
b2-4ac<0
例:利用二次函数的图象求一元二次方程x +x-1=0的近似解。
1
2
0
-1
-2
x
1
2
3
4
5
6
y
自己进行画图,得到近似解为
x1≈0.6,
x2≈-1.6
1.判断下列函数图象与x轴是否有公共点,并说明理由。
2.在上元中学校运会上,初三(8)班运动员掷铅球,铅球的高y(m)与水平距离x(m)之间的函数关系式为
y=-0.2x2+1.6x+1.8,则此运动员的成绩是 m。
3.已知二次函数y=x2-6x+8的图象,利用图象回答问题:
(1)方程x2-6x+8=0的解是什么?
(2)x取什么值时,y>0?
(3)x取什么值时,y<0?
4.若函数y=mx -6x+2图象与x轴只有一个公共点,求m的值。
1.通过这节课的学习活动你有哪些收获?
2.对这节课的学习,你还有什么想法吗?
感悟与反思
谢 谢
二次函数与一元二次方程
x
y
… -2 -1 0 1 2 3 4 …
… 5 0 -3 -4 -3 0 5 …
(1,-4)
写出二次函数 的顶点坐标、对称轴,并画出它的图象。
N
M
当x为何值时,y=0?
x=-1,x=3
探究一
一般地,如果二次函数y=ax2+bx+c的图象与x轴有两个公共点(x1,0)、(x2,0),那么一元二次方程ax2+bx+c=0有两个不相等的实数根x=x1、x=x2,反之亦成立。
不画图象,你能说出函数 的图象与x轴的交点坐标吗?
解:当y=0时,
解得:
所以,函数 的图象与x轴的交点坐标为(-3,0)和(2,0)。
探究二
观察二次函数y=x -6x+9的图象和二次函数y=x -2x+3的图象,分别说出一元二次方程x -6x+9=0和x -2x+3=0的根的情况。
二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0的根的关系?
二次函数y=ax2+bx+c的图象与x轴的交点 一元二次方程ax2+bx+c=0的根 b2-4ac
有两个交点
有两个不相等的实数根
b2-4ac>0
有一个交点
有两个相等的实数根
b2-4ac=0
没有交点
没有实数根
b2-4ac<0
例:利用二次函数的图象求一元二次方程x +x-1=0的近似解。
1
2
0
-1
-2
x
1
2
3
4
5
6
y
自己进行画图,得到近似解为
x1≈0.6,
x2≈-1.6
1.判断下列函数图象与x轴是否有公共点,并说明理由。
2.在上元中学校运会上,初三(8)班运动员掷铅球,铅球的高y(m)与水平距离x(m)之间的函数关系式为
y=-0.2x2+1.6x+1.8,则此运动员的成绩是 m。
3.已知二次函数y=x2-6x+8的图象,利用图象回答问题:
(1)方程x2-6x+8=0的解是什么?
(2)x取什么值时,y>0?
(3)x取什么值时,y<0?
4.若函数y=mx -6x+2图象与x轴只有一个公共点,求m的值。
1.通过这节课的学习活动你有哪些收获?
2.对这节课的学习,你还有什么想法吗?
感悟与反思
谢 谢
