沪科版数学八年级上册 11.2 图形在坐标系中的平移(4) 教案
文档属性
| 名称 | 沪科版数学八年级上册 11.2 图形在坐标系中的平移(4) 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 73.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 16:42:33 | ||
图片预览

文档简介
11.2 图形在坐标系中的平移 学习目标: 1.掌握坐标平面内图形平移的规律 2. 感受坐标平面内图形变换的坐标变化,发展数形结合思想,培养合作交流能力。 学习重点:掌握坐标平面内图形平移的规律 一、学前准备: 1.A是数轴一个点表示数5,现在我们把A往左平移3个单位得到B,向右平移2个单位得到C,你能说出B和C各表示什么数吗?B是_______, C是_________。 2.已知三角形ABC的三个顶点坐标分别是A(-3,-1), B(-2,-3),C(-1,-2)并把图形画在图1中 ① 将三角形三个顶点的横坐标都加3,得到三角形 ,在图2中画出这个图形 ② 将三角形的三个顶点的纵坐标都加2,得到三角形 ,在图3中画出图形 (
图
2
) (
图
1
) (
图
3
) 二、 自主学习: 1、探究点的平移与坐标的变化 平移前的点平移方向与单位长度平移后的点A(-2,-3)右5A1( )A(-2,-3)上4A2( )A(-2,-3)左3A3( )A(-2,-3)下2A4( )
平移前的点平移方向与单位长度平移后的点A(x,y)右aA(x,y)左aA(x,y)上bA(x,y)下b
2、探究图形的平移与其坐标的变化 图形左、右或上、下平移与点的坐标变化间的关系 (
向右平移
a
个单位长度
位
) 左、右平移: 原图形上的点(,) (___a, ); (
向左平移
a
个单位长度
)原图形上的点((,) (___a, ); (
向上平移
个
单位长度
)上、下平移: (
向下平移
个单位
长度
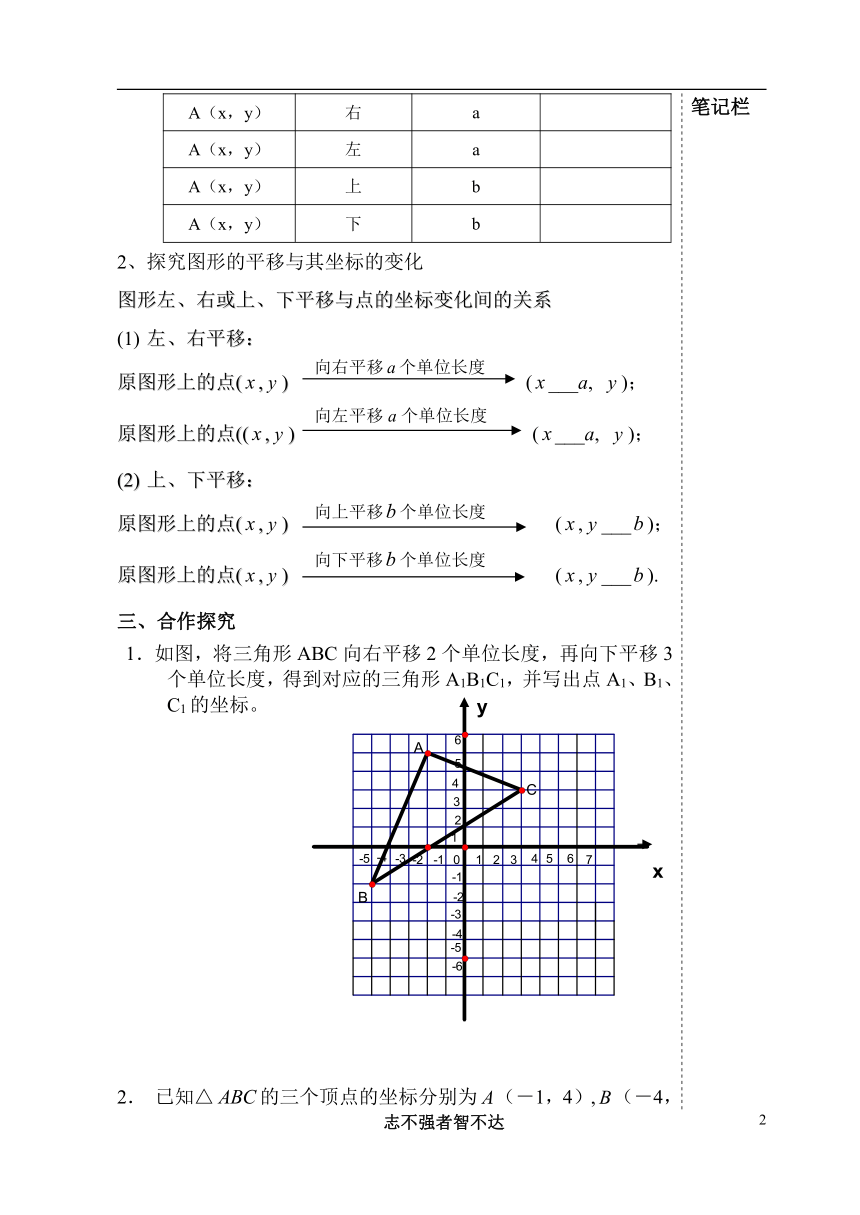
) 原图形上的点(,) (,___); 原图形上的点(,) (,___). 三、合作探究 1.如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1,并写出点A1、B1、C1的坐标。 2. 已知△的三个顶点的坐标分别为(-1,4),(-4,-1),(1,1),将△ 平移后得△,若的坐标为(4,3),求和的坐标并求出△的面积。 四、 自我测试: 1.已知点A的坐标为(-2,-3),分别求点经下列平移变换后所得的像的坐标。 (1)向上平移3个单位 (2)向下平移3个单位 (3)向左平移2个单位 (4)向右平移4个单位 (5)先向右平移3个单位,再向下平移3个单位 2.已知正方形的一个顶点(-4,2),把此正方形向上平移2个单位长度,再向左平移3个单位长度,此时的坐标为_______. 3.线段是由线段平移得到的,点(-1,4)的对应点为(4,7),则点(-4,-1)的对应点D的坐标为________。 4.在平面直角坐标系中,△三个顶点的横坐标保持不变,纵坐标都减去3,则得到的新三角形与原三角形相比向_______平移了3个单长度. 5.如下图所示,小芳在与同伴玩“找宝”游戏,他们准备到,,三个点去找宝,现已知点的坐标是(1,1),每格代表一个单位长度,则, 两点的坐标分别是_ 如图:铅笔图案的五个顶点的坐标分别是(0,1) (4,1) (5,1.5) (4,2) (0,2)将图案向下平移2个单位长度,作出相应图案,并写出平移后相应5点的坐标。 拓展与应用: 1、利用平移的知识求下图的周长 (
4
3
) 笔记栏 笔记栏 笔记栏 笔记栏
1
志不强者智不达
图
2
) (
图
1
) (
图
3
) 二、 自主学习: 1、探究点的平移与坐标的变化 平移前的点平移方向与单位长度平移后的点A(-2,-3)右5A1( )A(-2,-3)上4A2( )A(-2,-3)左3A3( )A(-2,-3)下2A4( )
平移前的点平移方向与单位长度平移后的点A(x,y)右aA(x,y)左aA(x,y)上bA(x,y)下b
2、探究图形的平移与其坐标的变化 图形左、右或上、下平移与点的坐标变化间的关系 (
向右平移
a
个单位长度
位
) 左、右平移: 原图形上的点(,) (___a, ); (
向左平移
a
个单位长度
)原图形上的点((,) (___a, ); (
向上平移
个
单位长度
)上、下平移: (
向下平移
个单位
长度
) 原图形上的点(,) (,___); 原图形上的点(,) (,___). 三、合作探究 1.如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1,并写出点A1、B1、C1的坐标。 2. 已知△的三个顶点的坐标分别为(-1,4),(-4,-1),(1,1),将△ 平移后得△,若的坐标为(4,3),求和的坐标并求出△的面积。 四、 自我测试: 1.已知点A的坐标为(-2,-3),分别求点经下列平移变换后所得的像的坐标。 (1)向上平移3个单位 (2)向下平移3个单位 (3)向左平移2个单位 (4)向右平移4个单位 (5)先向右平移3个单位,再向下平移3个单位 2.已知正方形的一个顶点(-4,2),把此正方形向上平移2个单位长度,再向左平移3个单位长度,此时的坐标为_______. 3.线段是由线段平移得到的,点(-1,4)的对应点为(4,7),则点(-4,-1)的对应点D的坐标为________。 4.在平面直角坐标系中,△三个顶点的横坐标保持不变,纵坐标都减去3,则得到的新三角形与原三角形相比向_______平移了3个单长度. 5.如下图所示,小芳在与同伴玩“找宝”游戏,他们准备到,,三个点去找宝,现已知点的坐标是(1,1),每格代表一个单位长度,则, 两点的坐标分别是_ 如图:铅笔图案的五个顶点的坐标分别是(0,1) (4,1) (5,1.5) (4,2) (0,2)将图案向下平移2个单位长度,作出相应图案,并写出平移后相应5点的坐标。 拓展与应用: 1、利用平移的知识求下图的周长 (
4
3
) 笔记栏 笔记栏 笔记栏 笔记栏
1
志不强者智不达
