3.3.2一元二次不等式(组)与线性规划课件-2021-2022学年高二上学期数学人教A版必修5(共23张PPT)
文档属性
| 名称 | 3.3.2一元二次不等式(组)与线性规划课件-2021-2022学年高二上学期数学人教A版必修5(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 657.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 10:32:57 | ||
图片预览






文档简介
(共23张PPT)
一元二次不等式(组)与简单的线性规划
探究二元一次不等式(组)的解集表示的图形
回忆:一元一次不等式(组)的解集--数集
图形---数轴上的区间。
如:不等式组
的解集为数轴上的一个区间(如图)。
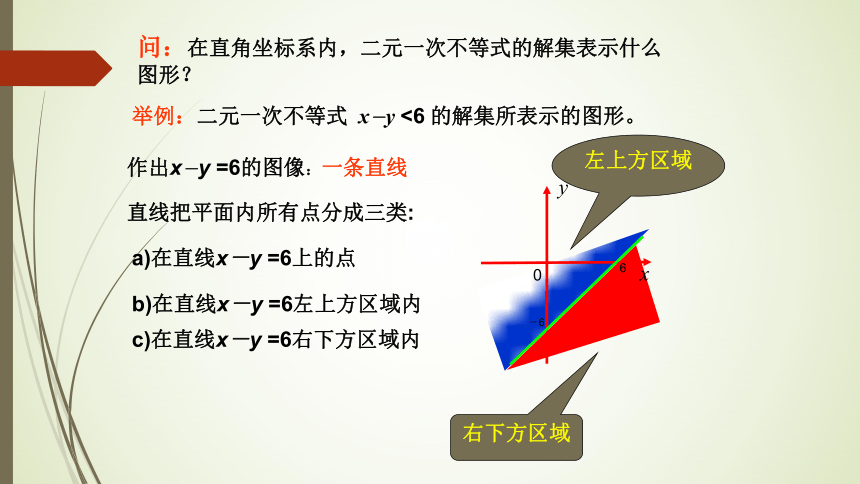
举例:二元一次不等式 x-y <6 的解集所表示的图形。
作出x-y =6的图像:一条直线
右下方区域
直线把平面内所有点分成三类:
a)在直线x-y =6上的点
b)在直线x-y =6左上方区域内
c)在直线x-y =6右下方区域内
左上方区域
x
y
0
6
-6
问:在直角坐标系内,二元一次不等式的解集表示什么图形?
●
6
-6
(0,0)
(3,-3)
(-2, 3)
(1,-6)
(7,0)
●
●
●
●
x
y
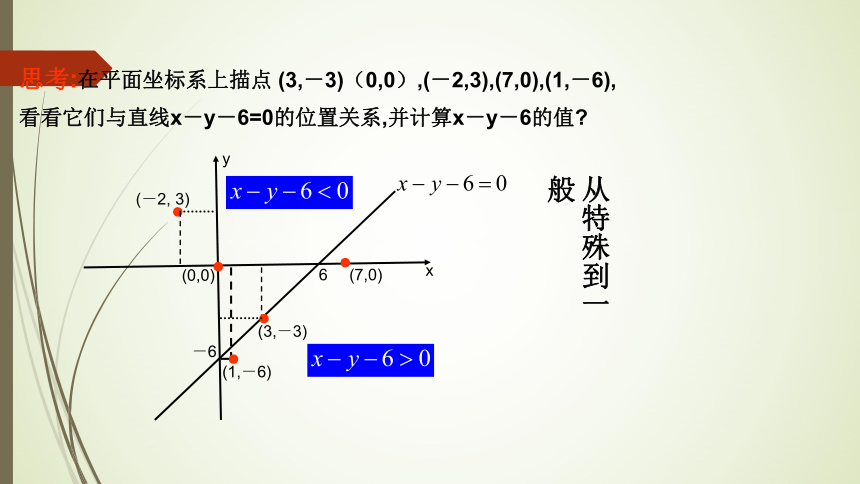
思考:在平面坐标系上描点 (3,-3)(0,0),(-2,3),(7,0),(1,-6),
看看它们与直线x-y-6=0的位置关系,并计算x-y-6的值
从特殊到一般
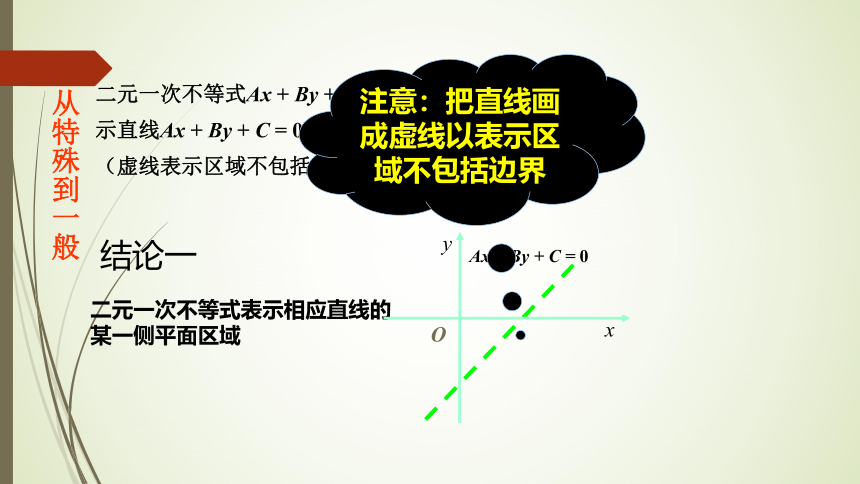
二元一次不等式Ax + By + C>0在平面直角坐标系中表示直线Ax + By + C = 0某一侧所有点组成的平面区域。(虚线表示区域不包括边界直线)
结论一
二元一次不等式表示相应直线的
某一侧平面区域
O
x
y
Ax + By + C = 0
从特殊到一般
注意:把直线画成虚线以表示区域不包括边界
问题2:如何判断二元一次不等式表示哪一侧的平面区域?
直线Ax+By+C=0同一侧的所有点(x,y)代入Ax+By+C所得实数的符号都相同,只需在直线的同一侧取某个特殊点(x0,y0)作为测试点,根据Ax0+By0+C的正负即可判断Ax+By+C>0表示直线的哪一侧区域.
结论二
直线定界,特殊点定域.
小诀窍
如果C≠0,可取(0,0);
如果C=0,可取(1,0)或(0,1).
从一般到特殊
2.二元一次不等式组表示的平面区域
(1)二元一次不等式组表示的平面区域是各个不等式表示的平面区域的________ ,即各个不等式表示的平面区域的公共部分.
(2)画二元一次不等式组表示的平面区域的一般步骤:直线定界,虚实分明,特殊点定域,优选原点,阴影表示.
(3)注意不等式中有无等号,无等号时直线画成________ ,有等号时直线画成________ ,特殊点一般选一个,当直线不过原点时,优先选原点.
交集
虚线
实线
【拓展】画二元一次不等式表示的平面区域的方法
(1)直线定界:不等式中无等号时直线画成虚线,有等号时直线画成实线.
(2)特殊点定域:若直线不过原点,特殊点常选原点;若直线过原点,则特殊点常选取或.
二、线性规划中的基本概念
【拓展】在通过求直线的截距的最值间接求出z的最值时,要注意:当时,截距取最大值时,z也取最大值;截距取最小值时,z也取最小值.当时,截距取最大值时,z取最小值;截距取最小值时,z取最大值.
例1.若x,y满足不等式组则的最大值为().
A.11B.11
C.13D.-13
A
[解析]将化为,作出可行域,如图中阴影部分所示,
当直线经过点D时,z取得最大值.
联立得,,此时,故选A.
例2[2020年全国Ⅲ卷]若满足约束条件则的最大值为_____.
7
[解析]作出不等式组表示的平面区域,如图中阴影部分(含边界)所示.由,得.由图可知,目标函数的最大值在点A处取得.由得,所以的最大值为3×1+2×2=7.
考点一 二元一次不等式(组)表示的平面区域
例1若不等式组表示的平面区域为三角形,且其面积等于,则实数m的值为_____.
1
[解析]如图,要使不等式组表示的平面区域为三角形,则,即.
由解得即.
由解得即,
又点的坐标为,
则,解得(舍去)或.
总结反思
(1)二元一次不等式(组)表示的平面区域的判断方法:直线定界,测试点定域.
(2)求平面区域的面积:
①先作出不等式组表示的平面区域,若不能直接作出,应利用题目的已知条件转化为不等式组问题,再作出平面区域.
②对平面区域进行分析,若为三角形应确定底与高;若为规则的四边形(如平行四边形或梯形),可利用面积公式直接求解;若为不规则四边形,可分割成几个三角形分别求解再求和.
考点二 求目标函数的最值问题
例2[2020年全国Ⅰ卷]若满足约束条件则的最大值为_____.
1
[解析]作出可行域,如图中阴影部分
所示,由得
故,0).作出直线,数形结合可知,
当直线过点A时,取得最大值,最大值为1.
总结反思
当目标函数是非线性函数时,常利用目标函数的几何意义来解题,常见代数式的几何意义:(1)表示点与原点的距离,表示点与点的距离;(2)表示点与原点连线的斜率,表示点与点连线的斜率.
考点三 线性规划中的参数问题
[解析]作出不等式组表示的平面区域如图所示,
由解得.
由图及线性规划知识可推测直线
必过点,得,经验证符合题目条件.
总结反思
求参数(参数的位置可能在目标函数中,也可能在约束条件中)的值或范围
(1)求解步骤:①注意对参数取值的讨论,将各种情况下的可行域画出来;②在符合题意的可行域中,寻求最优解.
(2)当目标函数中含有参数时,要根据临界位置确定参数所满足的条件.
数学建模——线性规划的实际应用
解线性规划应用问题的一般步骤:
(1)分析题意,设出未知量;
(2)列出线性约束条件和目标函数;
(3)作出可行域并利用数形结合求解;
(4)作答.
谢谢大家!
一元二次不等式(组)与简单的线性规划
探究二元一次不等式(组)的解集表示的图形
回忆:一元一次不等式(组)的解集--数集
图形---数轴上的区间。
如:不等式组
的解集为数轴上的一个区间(如图)。
举例:二元一次不等式 x-y <6 的解集所表示的图形。
作出x-y =6的图像:一条直线
右下方区域
直线把平面内所有点分成三类:
a)在直线x-y =6上的点
b)在直线x-y =6左上方区域内
c)在直线x-y =6右下方区域内
左上方区域
x
y
0
6
-6
问:在直角坐标系内,二元一次不等式的解集表示什么图形?
●
6
-6
(0,0)
(3,-3)
(-2, 3)
(1,-6)
(7,0)
●
●
●
●
x
y
思考:在平面坐标系上描点 (3,-3)(0,0),(-2,3),(7,0),(1,-6),
看看它们与直线x-y-6=0的位置关系,并计算x-y-6的值
从特殊到一般
二元一次不等式Ax + By + C>0在平面直角坐标系中表示直线Ax + By + C = 0某一侧所有点组成的平面区域。(虚线表示区域不包括边界直线)
结论一
二元一次不等式表示相应直线的
某一侧平面区域
O
x
y
Ax + By + C = 0
从特殊到一般
注意:把直线画成虚线以表示区域不包括边界
问题2:如何判断二元一次不等式表示哪一侧的平面区域?
直线Ax+By+C=0同一侧的所有点(x,y)代入Ax+By+C所得实数的符号都相同,只需在直线的同一侧取某个特殊点(x0,y0)作为测试点,根据Ax0+By0+C的正负即可判断Ax+By+C>0表示直线的哪一侧区域.
结论二
直线定界,特殊点定域.
小诀窍
如果C≠0,可取(0,0);
如果C=0,可取(1,0)或(0,1).
从一般到特殊
2.二元一次不等式组表示的平面区域
(1)二元一次不等式组表示的平面区域是各个不等式表示的平面区域的________ ,即各个不等式表示的平面区域的公共部分.
(2)画二元一次不等式组表示的平面区域的一般步骤:直线定界,虚实分明,特殊点定域,优选原点,阴影表示.
(3)注意不等式中有无等号,无等号时直线画成________ ,有等号时直线画成________ ,特殊点一般选一个,当直线不过原点时,优先选原点.
交集
虚线
实线
【拓展】画二元一次不等式表示的平面区域的方法
(1)直线定界:不等式中无等号时直线画成虚线,有等号时直线画成实线.
(2)特殊点定域:若直线不过原点,特殊点常选原点;若直线过原点,则特殊点常选取或.
二、线性规划中的基本概念
【拓展】在通过求直线的截距的最值间接求出z的最值时,要注意:当时,截距取最大值时,z也取最大值;截距取最小值时,z也取最小值.当时,截距取最大值时,z取最小值;截距取最小值时,z取最大值.
例1.若x,y满足不等式组则的最大值为().
A.11B.11
C.13D.-13
A
[解析]将化为,作出可行域,如图中阴影部分所示,
当直线经过点D时,z取得最大值.
联立得,,此时,故选A.
例2[2020年全国Ⅲ卷]若满足约束条件则的最大值为_____.
7
[解析]作出不等式组表示的平面区域,如图中阴影部分(含边界)所示.由,得.由图可知,目标函数的最大值在点A处取得.由得,所以的最大值为3×1+2×2=7.
考点一 二元一次不等式(组)表示的平面区域
例1若不等式组表示的平面区域为三角形,且其面积等于,则实数m的值为_____.
1
[解析]如图,要使不等式组表示的平面区域为三角形,则,即.
由解得即.
由解得即,
又点的坐标为,
则,解得(舍去)或.
总结反思
(1)二元一次不等式(组)表示的平面区域的判断方法:直线定界,测试点定域.
(2)求平面区域的面积:
①先作出不等式组表示的平面区域,若不能直接作出,应利用题目的已知条件转化为不等式组问题,再作出平面区域.
②对平面区域进行分析,若为三角形应确定底与高;若为规则的四边形(如平行四边形或梯形),可利用面积公式直接求解;若为不规则四边形,可分割成几个三角形分别求解再求和.
考点二 求目标函数的最值问题
例2[2020年全国Ⅰ卷]若满足约束条件则的最大值为_____.
1
[解析]作出可行域,如图中阴影部分
所示,由得
故,0).作出直线,数形结合可知,
当直线过点A时,取得最大值,最大值为1.
总结反思
当目标函数是非线性函数时,常利用目标函数的几何意义来解题,常见代数式的几何意义:(1)表示点与原点的距离,表示点与点的距离;(2)表示点与原点连线的斜率,表示点与点连线的斜率.
考点三 线性规划中的参数问题
[解析]作出不等式组表示的平面区域如图所示,
由解得.
由图及线性规划知识可推测直线
必过点,得,经验证符合题目条件.
总结反思
求参数(参数的位置可能在目标函数中,也可能在约束条件中)的值或范围
(1)求解步骤:①注意对参数取值的讨论,将各种情况下的可行域画出来;②在符合题意的可行域中,寻求最优解.
(2)当目标函数中含有参数时,要根据临界位置确定参数所满足的条件.
数学建模——线性规划的实际应用
解线性规划应用问题的一般步骤:
(1)分析题意,设出未知量;
(2)列出线性约束条件和目标函数;
(3)作出可行域并利用数形结合求解;
(4)作答.
谢谢大家!
