人教版数学七年级下册 5.2.2平行线的判定3 课件(共25张)
文档属性
| 名称 | 人教版数学七年级下册 5.2.2平行线的判定3 课件(共25张) |  | |
| 格式 | ppt | ||
| 文件大小 | 924.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 17:12:03 | ||
图片预览



文档简介
(共26张PPT)
5.2.2
平行线的判定
学习目标
1、掌握平行线的三种判定方法。并会运
用所学方法来判断两条直线是否平行。
2、会根据判定方法进行简单的推理并学
会用数学符号写出简单的推理过程。
3、体会数学中的转化思想。
1
2
观察思考
讨论交流
a
b
.
A
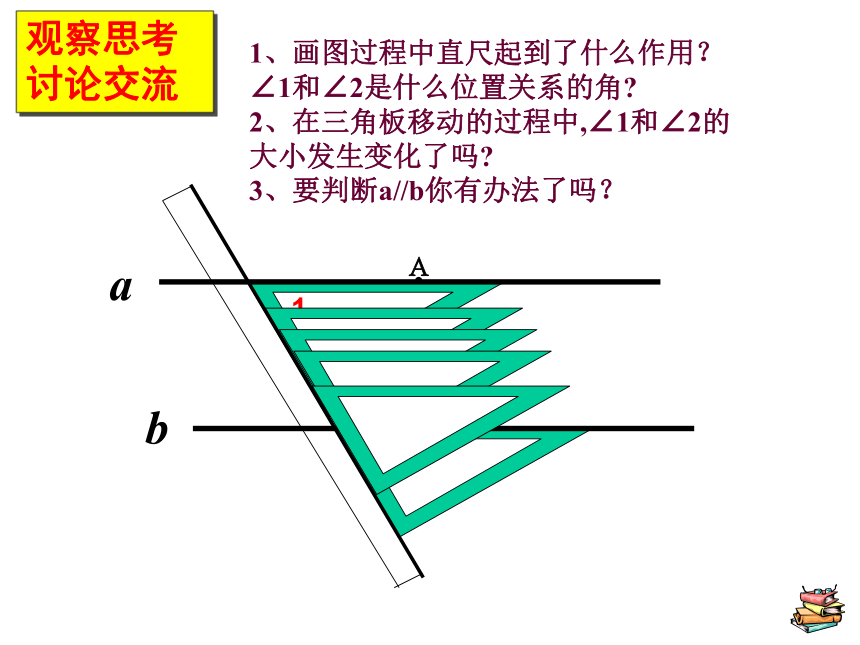
1、画图过程中直尺起到了什么作用? ∠1和∠2是什么位置关系的角
2、在三角板移动的过程中,∠1和∠2的大小发生变化了吗
3、要判断a//b你有办法了吗?
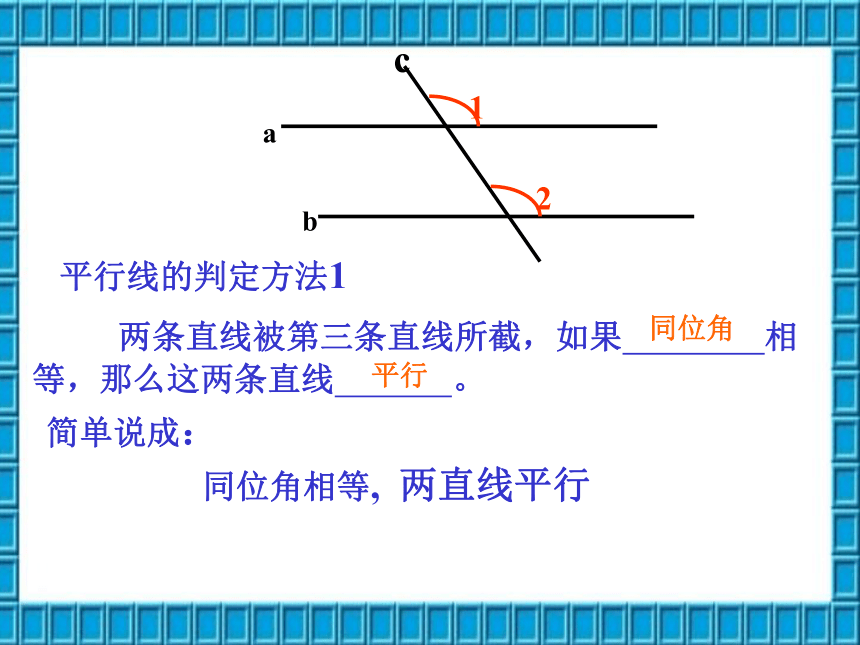
两条直线被第三条直线所截,如果 相等,那么这两条直线 。
简单说成:
同位角相等, 两直线平行
平行线的判定方法1
1
2
a
b
c
同位角
平行
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
思 考
a
b
c
1
2
3
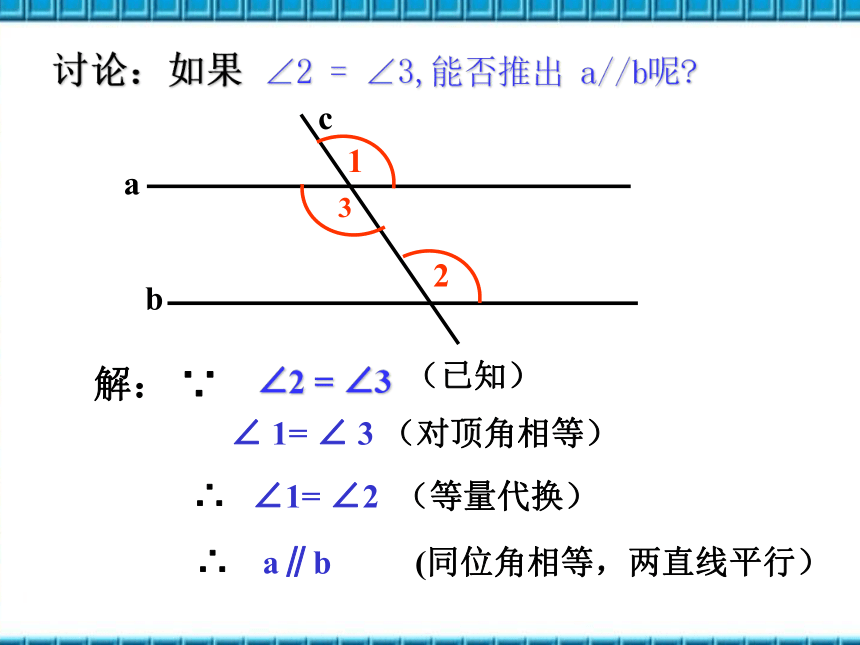
解: ∵
∠ 1= ∠ 3 (对顶角相等)
∴ ∠1= ∠2 (等量代换)
∴ a∥b (同位角相等,两直线平行)
讨论:如果 ∠2 = ∠3,能否推出 a//b呢
∠2 = ∠3
(已知)
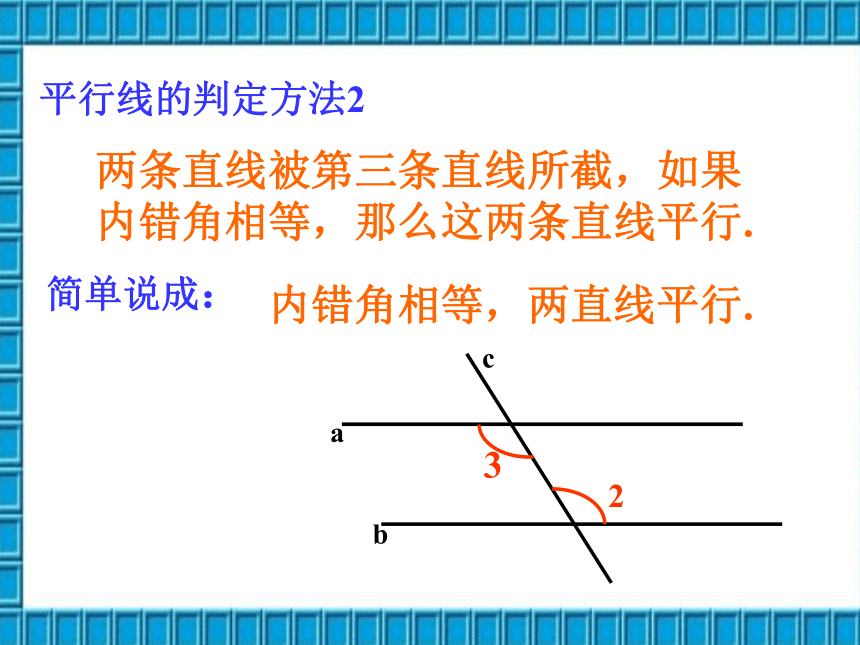
平行线的判定方法2
两条直线被第三条直线所截,如果
内错角相等,那么这两条直线平行.
内错角相等,两直线平行.
简单说成:
a
b
c
2
3
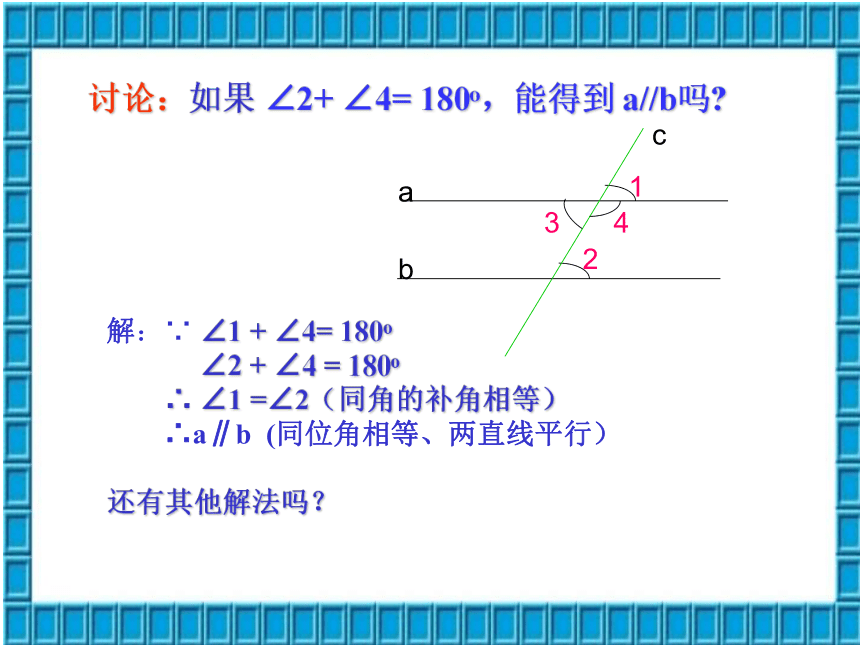
讨论:如果 ∠2+ ∠4= 180o,能得到 a//b吗
解:∵ ∠1 + ∠4= 180o
∠2 + ∠4 = 180o
∴ ∠1 =∠2(同角的补角相等)
∴a∥b (同位角相等、两直线平行)
还有其他解法吗?
a
b
c
1
2
3
4
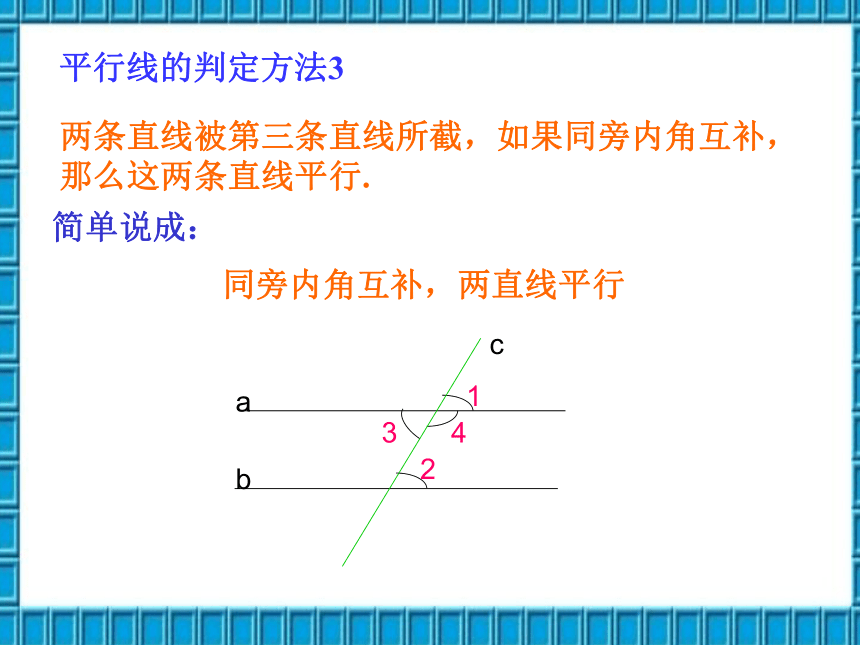
简单说成:
同旁内角互补,两直线平行
平行线的判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
a
b
c
1
2
3
4
a
b
1
2
l
直线a、b被直线l所截,已知∠1=1150 ∠2=1150,问直线a和直线b平行吗?为什么
解 ∵
∠1=1150
∠2=1150
∴∠1=∠2
∴a∥b
﹙内错角相等,两直线平行﹚
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
b
c
a
1
2
解:这两条直线平行。
∵ b⊥a c ⊥a
∴∠1=∠2 = 90 °
∴b ∥ c(同位角相等,两直线平行)
探 索
结论:垂直于同一条直线的两条直线互相( )
平行
同位角相等, 两直线平行
内错角相等,两直线平行.
同旁内角互补,两直线平行
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
在同一平面内,垂直于同一条直线的两条直线互相平行
如图,
如果∠B=∠1,则可得_______//_______
根据是________________________________
如果∠D=∠1,则可得到_______//_______
根据是____________________________
AD
BC
同位角相等,两直线平行
AB
CD
内错角相等,两直线平行
如图,四边形ABCD中,已知∠B=60°,∠C=120°,AB与CD平行吗?AD与BC平行吗?
解:直线AB与CD平行,
∵∠B=60°,∠C=120°
∴∠B+C=180°,
∴AB//CD(同旁内角互补,两直线平行)
根据题目条件无法判定AD与BC平行。
如图,直线a,b被c所截,已知∠1=120°,∠2=60°,直线a,b平行吗?为什么?
解:a与b平行,
∵∠1=∠3(对顶角相等)
∠1=120°(已知)
∴∠3=120°
∵∠2=60°
∴∠2+3=180°
∴a//b(同旁内角互补,两直线平行)
a
b
c
1
2
3
① ∵ ∠2 =___(已知)
∴ ___∥___
② ∵ ∠3 = ∠5(已知)
∴ ___∥___
③∵ ∠4 +___=180o(已知)
∴ ___∥___
∠6
AB
CD
AB
CD
∠5
AB
CD
A
C
1
4
2
3
5
8
6
7
B
D
2.如图:
平行线的识别
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
① ∵ ∠1 =_____(已知)
∴ AB∥CE
② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF
③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB
平行线的识别
∠3
∠3
3.如图:
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
已知: ∠1=75o , ∠2 =105o
问:AB与CD平行吗?
为什么?
平行线的识别
4.如图:
A
C
1
4
2
3
B
D
5
例题1.
① ∵ ∠1 =_____ (已知)
∴ AB∥CE
② ∵ ∠2 = (已知)
∴ CD∥BF
③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____
AB
CE
∠2
∠4
如图:
1
3
5
4
2
C
F
E
A
D
B
(内错角相等,两直线平行)
(同位角相等,两直线平行)
(同旁内角互补,两直线平行)
已知∠3=45 °,∠1与∠2互余,你能得到 ?
解∵∠1+∠2=90° ∠1=∠2
∴∠1=∠2=45°
∵ ∠3=45°
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)
1
2
3
A
B
C
D
AB//CD
例题2
(1)∵∠1=∠B(已知)
∴__∥__(
(4)∵∠_ = ∠_(已知)
∴AB∥CD( )
AD BC 同位角相等,两直线平行)
(2)∵∠1=∠D(已知)
∴ ∥ ( )
(3)∵∠B+∠BAD=180°(已知)
∴ ∥ ( )
3 5
内错角相等,两直线平行
AB DC 内错角相等,两直线平行
AD BC 同旁内角互补,两直线平行
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定示意图
判定
数量关系
位置关系
体验成功——达标检测
2、直线a、b与直线c相交,给出下列条件:
①∠1= ∠2②∠3= ∠6③∠4+∠7=1800
④∠3+ ∠5=1800,其中能判断a//b的是
( )
A ①②③④ B ①③④ C ①③ D ④
6
4
1
5
7
3
2
8
a
b
B
∠ C=61
当∠ABE= 度时,EF∥CN
当∠CBF= 度时,EF∥CN
。
3、如图
A
B
C
N
E
F
必做题:
1、如果∠A +∠B =180°,那么根据同旁内
角互补,两直线平行,可得_____∥_____;
如果 +∠B =180°,那么根据同旁内角
互补,两直线平行,可得AB∥EC。
A
B
C
E
AE BC
61
61
∠C
如图,BC、DE分别平分 ABD和 BDF,且 1= 2,请找出平行线,并说明理由。
选 做 题
A
B
D
F
C
E
2
1
3
4
1.如图,直线a、b被直线c所截,若∠1+∠2=180°,那么直线a与直线b平行吗?为什么?
解:∵∠1+∠2=180°(已知)
∠1+∠3=180°(互补的定义)
∴∠2=∠3(同角的补角相等)
∴a//b(内错角相等,两直线平行)
5.2.2
平行线的判定
学习目标
1、掌握平行线的三种判定方法。并会运
用所学方法来判断两条直线是否平行。
2、会根据判定方法进行简单的推理并学
会用数学符号写出简单的推理过程。
3、体会数学中的转化思想。
1
2
观察思考
讨论交流
a
b
.
A
1、画图过程中直尺起到了什么作用? ∠1和∠2是什么位置关系的角
2、在三角板移动的过程中,∠1和∠2的大小发生变化了吗
3、要判断a//b你有办法了吗?
两条直线被第三条直线所截,如果 相等,那么这两条直线 。
简单说成:
同位角相等, 两直线平行
平行线的判定方法1
1
2
a
b
c
同位角
平行
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
思 考
a
b
c
1
2
3
解: ∵
∠ 1= ∠ 3 (对顶角相等)
∴ ∠1= ∠2 (等量代换)
∴ a∥b (同位角相等,两直线平行)
讨论:如果 ∠2 = ∠3,能否推出 a//b呢
∠2 = ∠3
(已知)
平行线的判定方法2
两条直线被第三条直线所截,如果
内错角相等,那么这两条直线平行.
内错角相等,两直线平行.
简单说成:
a
b
c
2
3
讨论:如果 ∠2+ ∠4= 180o,能得到 a//b吗
解:∵ ∠1 + ∠4= 180o
∠2 + ∠4 = 180o
∴ ∠1 =∠2(同角的补角相等)
∴a∥b (同位角相等、两直线平行)
还有其他解法吗?
a
b
c
1
2
3
4
简单说成:
同旁内角互补,两直线平行
平行线的判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
a
b
c
1
2
3
4
a
b
1
2
l
直线a、b被直线l所截,已知∠1=1150 ∠2=1150,问直线a和直线b平行吗?为什么
解 ∵
∠1=1150
∠2=1150
∴∠1=∠2
∴a∥b
﹙内错角相等,两直线平行﹚
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
b
c
a
1
2
解:这两条直线平行。
∵ b⊥a c ⊥a
∴∠1=∠2 = 90 °
∴b ∥ c(同位角相等,两直线平行)
探 索
结论:垂直于同一条直线的两条直线互相( )
平行
同位角相等, 两直线平行
内错角相等,两直线平行.
同旁内角互补,两直线平行
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
在同一平面内,垂直于同一条直线的两条直线互相平行
如图,
如果∠B=∠1,则可得_______//_______
根据是________________________________
如果∠D=∠1,则可得到_______//_______
根据是____________________________
AD
BC
同位角相等,两直线平行
AB
CD
内错角相等,两直线平行
如图,四边形ABCD中,已知∠B=60°,∠C=120°,AB与CD平行吗?AD与BC平行吗?
解:直线AB与CD平行,
∵∠B=60°,∠C=120°
∴∠B+C=180°,
∴AB//CD(同旁内角互补,两直线平行)
根据题目条件无法判定AD与BC平行。
如图,直线a,b被c所截,已知∠1=120°,∠2=60°,直线a,b平行吗?为什么?
解:a与b平行,
∵∠1=∠3(对顶角相等)
∠1=120°(已知)
∴∠3=120°
∵∠2=60°
∴∠2+3=180°
∴a//b(同旁内角互补,两直线平行)
a
b
c
1
2
3
① ∵ ∠2 =___(已知)
∴ ___∥___
② ∵ ∠3 = ∠5(已知)
∴ ___∥___
③∵ ∠4 +___=180o(已知)
∴ ___∥___
∠6
AB
CD
AB
CD
∠5
AB
CD
A
C
1
4
2
3
5
8
6
7
B
D
2.如图:
平行线的识别
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
① ∵ ∠1 =_____(已知)
∴ AB∥CE
② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF
③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB
平行线的识别
∠3
∠3
3.如图:
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
已知: ∠1=75o , ∠2 =105o
问:AB与CD平行吗?
为什么?
平行线的识别
4.如图:
A
C
1
4
2
3
B
D
5
例题1.
① ∵ ∠1 =_____ (已知)
∴ AB∥CE
② ∵ ∠2 = (已知)
∴ CD∥BF
③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____
AB
CE
∠2
∠4
如图:
1
3
5
4
2
C
F
E
A
D
B
(内错角相等,两直线平行)
(同位角相等,两直线平行)
(同旁内角互补,两直线平行)
已知∠3=45 °,∠1与∠2互余,你能得到 ?
解∵∠1+∠2=90° ∠1=∠2
∴∠1=∠2=45°
∵ ∠3=45°
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)
1
2
3
A
B
C
D
AB//CD
例题2
(1)∵∠1=∠B(已知)
∴__∥__(
(4)∵∠_ = ∠_(已知)
∴AB∥CD( )
AD BC 同位角相等,两直线平行)
(2)∵∠1=∠D(已知)
∴ ∥ ( )
(3)∵∠B+∠BAD=180°(已知)
∴ ∥ ( )
3 5
内错角相等,两直线平行
AB DC 内错角相等,两直线平行
AD BC 同旁内角互补,两直线平行
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定示意图
判定
数量关系
位置关系
体验成功——达标检测
2、直线a、b与直线c相交,给出下列条件:
①∠1= ∠2②∠3= ∠6③∠4+∠7=1800
④∠3+ ∠5=1800,其中能判断a//b的是
( )
A ①②③④ B ①③④ C ①③ D ④
6
4
1
5
7
3
2
8
a
b
B
∠ C=61
当∠ABE= 度时,EF∥CN
当∠CBF= 度时,EF∥CN
。
3、如图
A
B
C
N
E
F
必做题:
1、如果∠A +∠B =180°,那么根据同旁内
角互补,两直线平行,可得_____∥_____;
如果 +∠B =180°,那么根据同旁内角
互补,两直线平行,可得AB∥EC。
A
B
C
E
AE BC
61
61
∠C
如图,BC、DE分别平分 ABD和 BDF,且 1= 2,请找出平行线,并说明理由。
选 做 题
A
B
D
F
C
E
2
1
3
4
1.如图,直线a、b被直线c所截,若∠1+∠2=180°,那么直线a与直线b平行吗?为什么?
解:∵∠1+∠2=180°(已知)
∠1+∠3=180°(互补的定义)
∴∠2=∠3(同角的补角相等)
∴a//b(内错角相等,两直线平行)
