4.2.2等差数列的前n项和公式课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册(16张PPT)
文档属性
| 名称 | 4.2.2等差数列的前n项和公式课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册(16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 10:40:48 | ||
图片预览





文档简介
数学
第四章 数列
4.2等差数列
4.2.2.1等差数列的前n项和
新课引入
数学王子——高斯
新教材《选择性必修二》
问题1 请同学们欣赏唐代诗人张南史的《花》并回答下面的问题:
花, 花.
深浅, 芬葩.
凝为雪, 错为霞.
莺和蝶到, 苑占宫遮.
已迷金谷路, 频驻玉人车.
芳草欲陵芳树, 东家半落西家.
愿得春风相伴去, 一攀一折向天涯.
从数学的角度来看,这首诗有什么特点?这首诗的内容一共有多少个字?
探究新知
新知学习
新教材《选择性必修二》
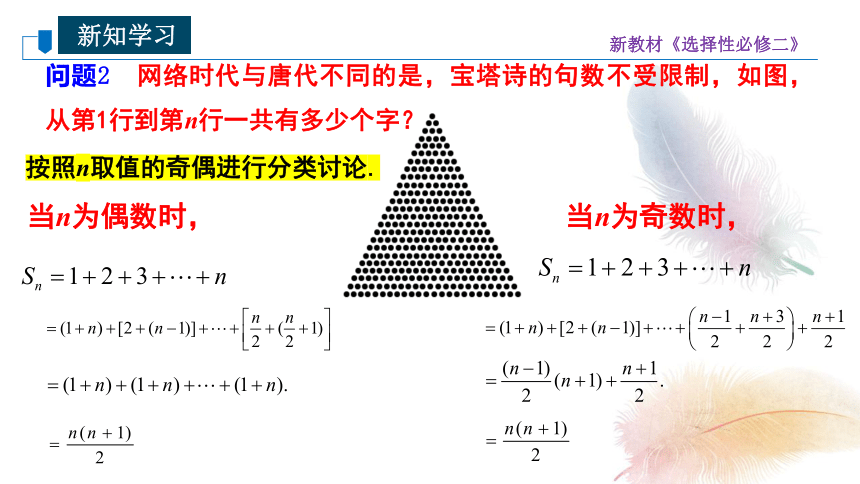
问题2 网络时代与唐代不同的是,宝塔诗的句数不受限制,如图,从第1行到第n行一共有多少个字?
按照n取值的奇偶进行分类讨论.
当n为偶数时,
当n为奇数时,
探究新知
新知学习
新教材《选择性必修二》
问题3 如何避免n取值奇偶的讨论呢?
组合
将倒置、组合的过程用数学表达式,可以表述为:
所以,
两式相加,得
倒序相加法
探究新知
新知学习
新教材《选择性必修二》
两式左右分别相加,得
问题4 上述方法的巧妙之处在哪里?这种方法能够推广到求等差数列????????的前????项和吗?
?
探究新知
倒序相加法
在等差数列{an}中,若m+n=p+q,则am+an=ap+aq.
新知学习
新教材《选择性必修二》
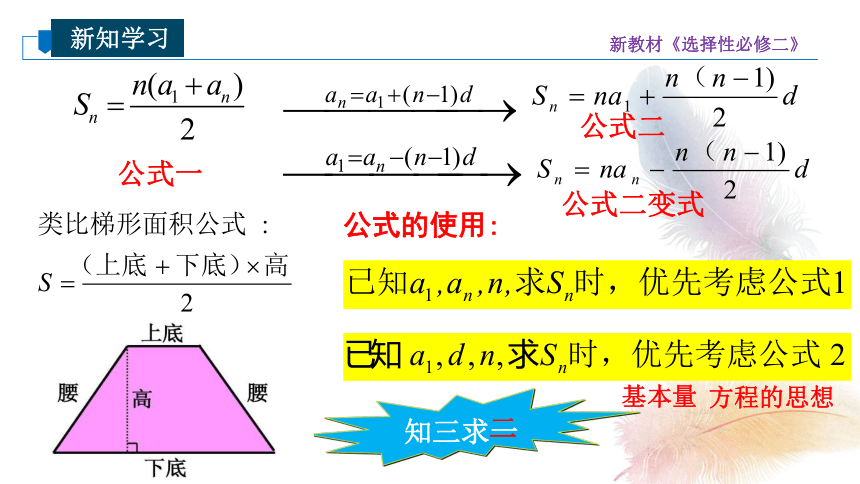
公式一
公式二
公式的使用:
探究新知
知三求一
二
新知学习
基本量
方程的思想
公式二变式
新教材《选择性必修二》
分析:对于(1),可以直接利用公式????????=????(????1+????????)2求和;
对于(2),可以先利用a1和????2的值求出d ,再利用公式????????=????????1+????(?????1)2 ????求和;
对于(3),已知公式????????=????????1+????(?????1)2 ????中的????1,????和????????,解方程即可求得????.
?
例1.已知数列{an}是等差数列.
(1)若a1=7, ????50=101,求????50;
(2)若a1=2, ????2= 52,求????10;
(3)若????1=12,d= ? 16, ????????= ?5,求???? .
?
典型例题
新教材《选择性必修二》
解:(1)因为a1=7, ????50=101 ,根据公式????????=????(????1+????????)2,可得????20=50×(7+101)2=2700.
(2)因为a1=2, ????2= 52, 所以d= 12.根据公式????????=????????1+????(?????1)2 ????,
可得????10=10×2+10×(10?1)2 ×12 = 852
(3)把????1=12,d= ? 16, ????????= ?5代入????????=????????1+????(?????1)2 ????,得?5=12????+????(?????1)2 ×(?16)
整理,得????2?7?????60=0解得????=12或????=?5(舍),所以????=12
?
例1.已知数列{an}是等差数列.
(1)若a1=7, ????50=101,求????50;
(2)若a1=2, ????2= 52,求????10;
(3)若????1=12,d= ? 16, ????????= ?5,求???? .
?
典例解析
典型例题
新教材《选择性必修二》
跟踪训练
跟踪训练1 在等差数列{an}中:
(1)a1=1,a4=7,求S9;
(2)a3+a15=40,求S17;
巩固练习
新教材《选择性必修二》
探索新知
问题5 等差数列通项公式是关于n的一次函数,前n项和呢?
待定系数法求解
新知学习
新教材《选择性必修二》
典例分析
例2.等差数列{an}的前n项和Sn=-n2+n,则它的通项公式是an=_____________.
方法1 当n=1时,a1=S1=-1+1=0;
当n≥2且n∈N*时,an=Sn-Sn-1=(-n2+n)-[-(n-1)2+(n-1)]=-2n+2,
经检验,n=1也适合该式.故an=-2n+2(n∈N*).
典型例题
新教材《选择性必修二》
例3.已知一个等差数列???????? 前10项的和是310,前20项的和是1220.由这些条件能确定这个等差数列的首项和公差吗?
?
典例解析
(法一)解:由题意,知S10=310, S20=1220,
把它们代入公式??????????=????????1+????(?????1)2 ????
得10????1+45?d?=31020????1+190?d?=1220
解方程组,得????1=4d?=6
所以,由所给的条件可以确定等差数列的首项和公差.
?
一般地,对于等差数列,只要给定两个相互独立的条件,这个数列就完全确定.
典型例题
新教材《选择性必修二》
体验高考
直击高考
体验高考
回顾小结
学了哪些知识
用了哪些方法
倒序相加法
方程思想
基本量思想
在等差数列{an}中,若m+n=p+q,则am+an=ap+aq.
本部分内容讲解结束
按ESC键退出全屏播放
第四章 数列
4.2等差数列
4.2.2.1等差数列的前n项和
新课引入
数学王子——高斯
新教材《选择性必修二》
问题1 请同学们欣赏唐代诗人张南史的《花》并回答下面的问题:
花, 花.
深浅, 芬葩.
凝为雪, 错为霞.
莺和蝶到, 苑占宫遮.
已迷金谷路, 频驻玉人车.
芳草欲陵芳树, 东家半落西家.
愿得春风相伴去, 一攀一折向天涯.
从数学的角度来看,这首诗有什么特点?这首诗的内容一共有多少个字?
探究新知
新知学习
新教材《选择性必修二》
问题2 网络时代与唐代不同的是,宝塔诗的句数不受限制,如图,从第1行到第n行一共有多少个字?
按照n取值的奇偶进行分类讨论.
当n为偶数时,
当n为奇数时,
探究新知
新知学习
新教材《选择性必修二》
问题3 如何避免n取值奇偶的讨论呢?
组合
将倒置、组合的过程用数学表达式,可以表述为:
所以,
两式相加,得
倒序相加法
探究新知
新知学习
新教材《选择性必修二》
两式左右分别相加,得
问题4 上述方法的巧妙之处在哪里?这种方法能够推广到求等差数列????????的前????项和吗?
?
探究新知
倒序相加法
在等差数列{an}中,若m+n=p+q,则am+an=ap+aq.
新知学习
新教材《选择性必修二》
公式一
公式二
公式的使用:
探究新知
知三求一
二
新知学习
基本量
方程的思想
公式二变式
新教材《选择性必修二》
分析:对于(1),可以直接利用公式????????=????(????1+????????)2求和;
对于(2),可以先利用a1和????2的值求出d ,再利用公式????????=????????1+????(?????1)2 ????求和;
对于(3),已知公式????????=????????1+????(?????1)2 ????中的????1,????和????????,解方程即可求得????.
?
例1.已知数列{an}是等差数列.
(1)若a1=7, ????50=101,求????50;
(2)若a1=2, ????2= 52,求????10;
(3)若????1=12,d= ? 16, ????????= ?5,求???? .
?
典型例题
新教材《选择性必修二》
解:(1)因为a1=7, ????50=101 ,根据公式????????=????(????1+????????)2,可得????20=50×(7+101)2=2700.
(2)因为a1=2, ????2= 52, 所以d= 12.根据公式????????=????????1+????(?????1)2 ????,
可得????10=10×2+10×(10?1)2 ×12 = 852
(3)把????1=12,d= ? 16, ????????= ?5代入????????=????????1+????(?????1)2 ????,得?5=12????+????(?????1)2 ×(?16)
整理,得????2?7?????60=0解得????=12或????=?5(舍),所以????=12
?
例1.已知数列{an}是等差数列.
(1)若a1=7, ????50=101,求????50;
(2)若a1=2, ????2= 52,求????10;
(3)若????1=12,d= ? 16, ????????= ?5,求???? .
?
典例解析
典型例题
新教材《选择性必修二》
跟踪训练
跟踪训练1 在等差数列{an}中:
(1)a1=1,a4=7,求S9;
(2)a3+a15=40,求S17;
巩固练习
新教材《选择性必修二》
探索新知
问题5 等差数列通项公式是关于n的一次函数,前n项和呢?
待定系数法求解
新知学习
新教材《选择性必修二》
典例分析
例2.等差数列{an}的前n项和Sn=-n2+n,则它的通项公式是an=_____________.
方法1 当n=1时,a1=S1=-1+1=0;
当n≥2且n∈N*时,an=Sn-Sn-1=(-n2+n)-[-(n-1)2+(n-1)]=-2n+2,
经检验,n=1也适合该式.故an=-2n+2(n∈N*).
典型例题
新教材《选择性必修二》
例3.已知一个等差数列???????? 前10项的和是310,前20项的和是1220.由这些条件能确定这个等差数列的首项和公差吗?
?
典例解析
(法一)解:由题意,知S10=310, S20=1220,
把它们代入公式??????????=????????1+????(?????1)2 ????
得10????1+45?d?=31020????1+190?d?=1220
解方程组,得????1=4d?=6
所以,由所给的条件可以确定等差数列的首项和公差.
?
一般地,对于等差数列,只要给定两个相互独立的条件,这个数列就完全确定.
典型例题
新教材《选择性必修二》
体验高考
直击高考
体验高考
回顾小结
学了哪些知识
用了哪些方法
倒序相加法
方程思想
基本量思想
在等差数列{an}中,若m+n=p+q,则am+an=ap+aq.
本部分内容讲解结束
按ESC键退出全屏播放
