3.3.3 函数的最大(小)值与导数课件-2021-2022学年高二上学期数学人教A版选修1-1(共15张PPT)
文档属性
| 名称 | 3.3.3 函数的最大(小)值与导数课件-2021-2022学年高二上学期数学人教A版选修1-1(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 735.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
3.3.3 函数的最大(小)值与导数
人教A版选修1-1
学习目标
1.能够区分极值与最值两个不同的概念。
2.会求闭区间上函数的最大值、最小值。
重点:利用导数求函数的最大值与最小值的方法。
难点:函数的最大值、最小值与函数的极大值、极小值得区别与联系。
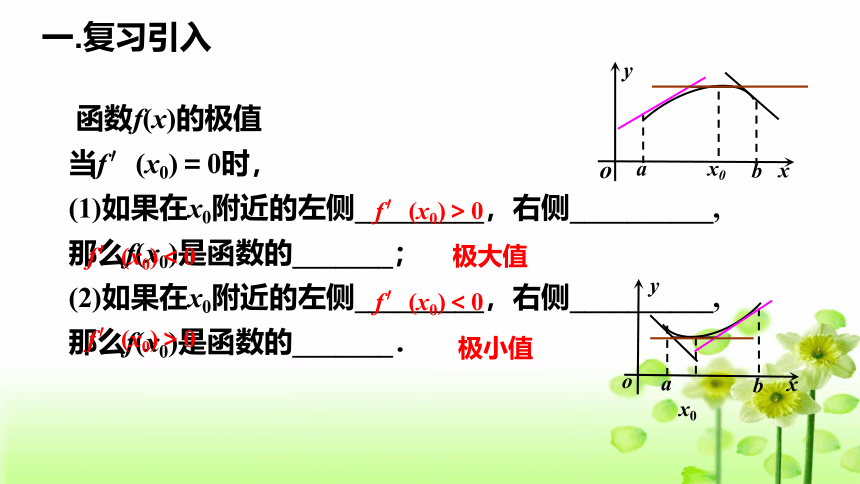
函数f(x)的极值
当f′(x0)=0时,
(1)如果在x0附近的左侧_________,右侧__________,那么f(x0)是函数的_______;
(2)如果在x0附近的左侧_________,右侧__________,那么f(x0)是函数的_______.
f′(x0)>0
f′(x0)<0
极大值
f′(x0)<0
f′(x0)>0
极小值
一.复习引入
o
a
x0
b
x
y
o
a
x0
b
x
y
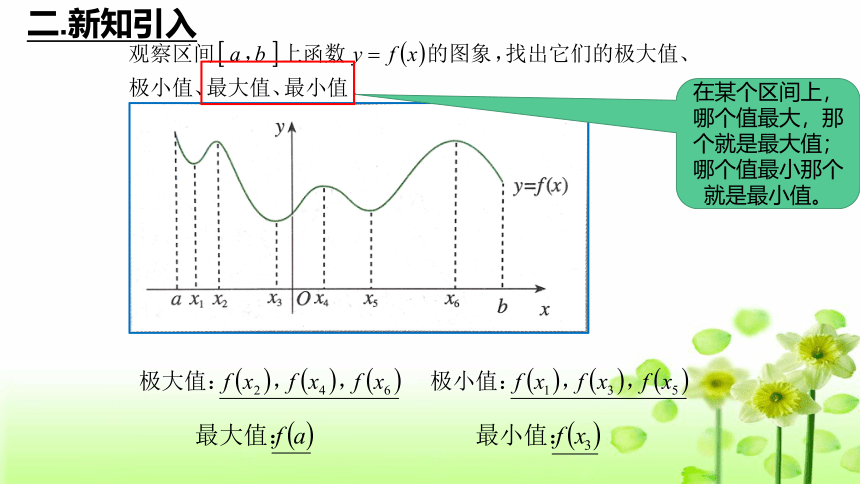
二.新知引入
在某个区间上,哪个值最大,那个就是最大值;哪个值最小那个就是最小值。
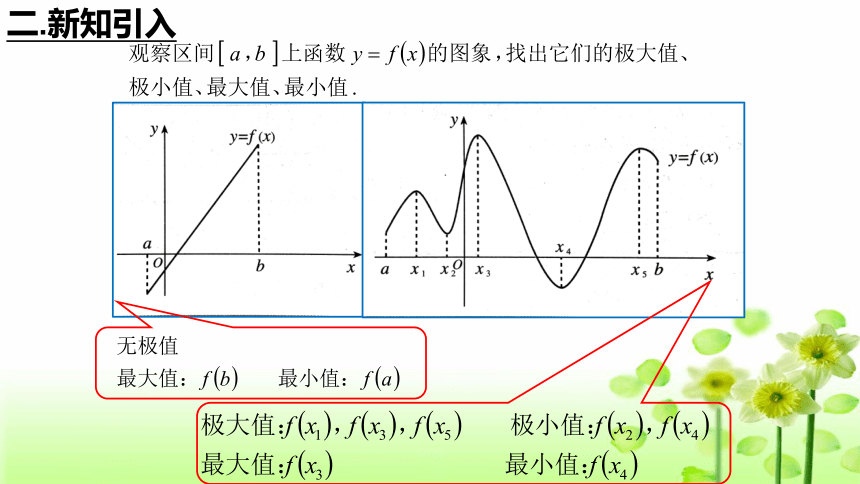
二.新知引入
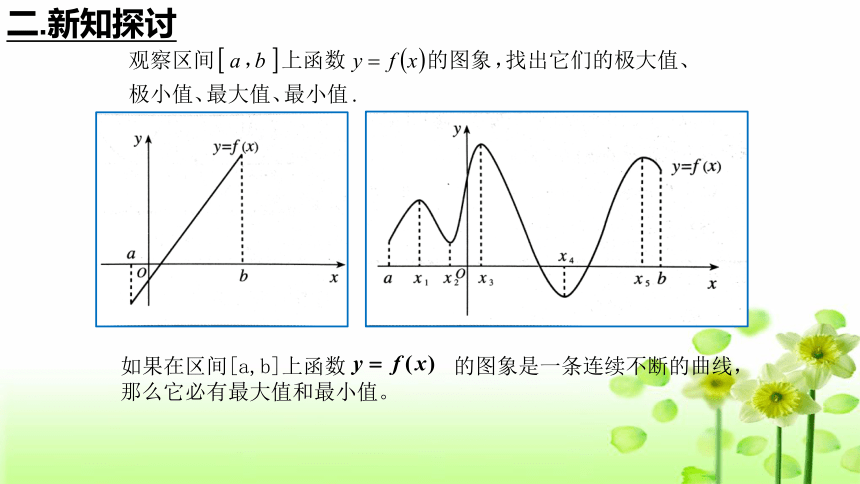
二.新知探讨
如果在区间[a,b]上函数 的图象是一条连续不断的曲线,那么它必有最大值和最小值。
三新知讲解
问题:
函数在[a,b]上的连续函数必有最大值与最小值,
那么,在(a,b)内的连续函数一定有最大值与最小值吗?
o
x
y
a
b
o
x
y
a
b
o
x
y
a
b
o
x
y
a
b
y=f(x)
y=f(x)
y=f(x)
y=f(x)
在开区间(a,b)内的连续函数不一定有最大值与
最小值.
怎么样求最值呢?求最值的步骤呢
四.练一练1
(P97)例5.已知函数 ,求f(x)在区间[0,3]上的
最大值和最小值.
x (0.2) 2 (2,3)
y′ - 0 +
y 递减 递增
五.例题讲解
(2) 将y=f(x)的各极值与f(a)、f(b)(端点处)
比较,其中最大的一个为最大值,最小的
一个最小值.
求f(x)在闭区间[a,b]上的最值的步骤:
(1) 求f(x)在区间(a,b)内极值(极大值或极小值);
注意:
1.在定义域内, 最值唯一;极值不唯一
2.最大值一定比最小值大.
3.极值是局部性质,最值是整体性质
练一练2
(P98)求下列函数在给定区间上的最大值与最小值:
小 结
求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下:
(1)求函数y=f(x)在(a,b)内的极值;
(2)将函数y=f(x)的各极值与端点处的函数值f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
作 业
习题3.3A组第6题
3.3.3 函数的最大(小)值与导数
人教A版选修1-1
学习目标
1.能够区分极值与最值两个不同的概念。
2.会求闭区间上函数的最大值、最小值。
重点:利用导数求函数的最大值与最小值的方法。
难点:函数的最大值、最小值与函数的极大值、极小值得区别与联系。
函数f(x)的极值
当f′(x0)=0时,
(1)如果在x0附近的左侧_________,右侧__________,那么f(x0)是函数的_______;
(2)如果在x0附近的左侧_________,右侧__________,那么f(x0)是函数的_______.
f′(x0)>0
f′(x0)<0
极大值
f′(x0)<0
f′(x0)>0
极小值
一.复习引入
o
a
x0
b
x
y
o
a
x0
b
x
y
二.新知引入
在某个区间上,哪个值最大,那个就是最大值;哪个值最小那个就是最小值。
二.新知引入
二.新知探讨
如果在区间[a,b]上函数 的图象是一条连续不断的曲线,那么它必有最大值和最小值。
三新知讲解
问题:
函数在[a,b]上的连续函数必有最大值与最小值,
那么,在(a,b)内的连续函数一定有最大值与最小值吗?
o
x
y
a
b
o
x
y
a
b
o
x
y
a
b
o
x
y
a
b
y=f(x)
y=f(x)
y=f(x)
y=f(x)
在开区间(a,b)内的连续函数不一定有最大值与
最小值.
怎么样求最值呢?求最值的步骤呢
四.练一练1
(P97)例5.已知函数 ,求f(x)在区间[0,3]上的
最大值和最小值.
x (0.2) 2 (2,3)
y′ - 0 +
y 递减 递增
五.例题讲解
(2) 将y=f(x)的各极值与f(a)、f(b)(端点处)
比较,其中最大的一个为最大值,最小的
一个最小值.
求f(x)在闭区间[a,b]上的最值的步骤:
(1) 求f(x)在区间(a,b)内极值(极大值或极小值);
注意:
1.在定义域内, 最值唯一;极值不唯一
2.最大值一定比最小值大.
3.极值是局部性质,最值是整体性质
练一练2
(P98)求下列函数在给定区间上的最大值与最小值:
小 结
求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下:
(1)求函数y=f(x)在(a,b)内的极值;
(2)将函数y=f(x)的各极值与端点处的函数值f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
作 业
习题3.3A组第6题
