八年级数学等腰三角形课件
图片预览




文档简介
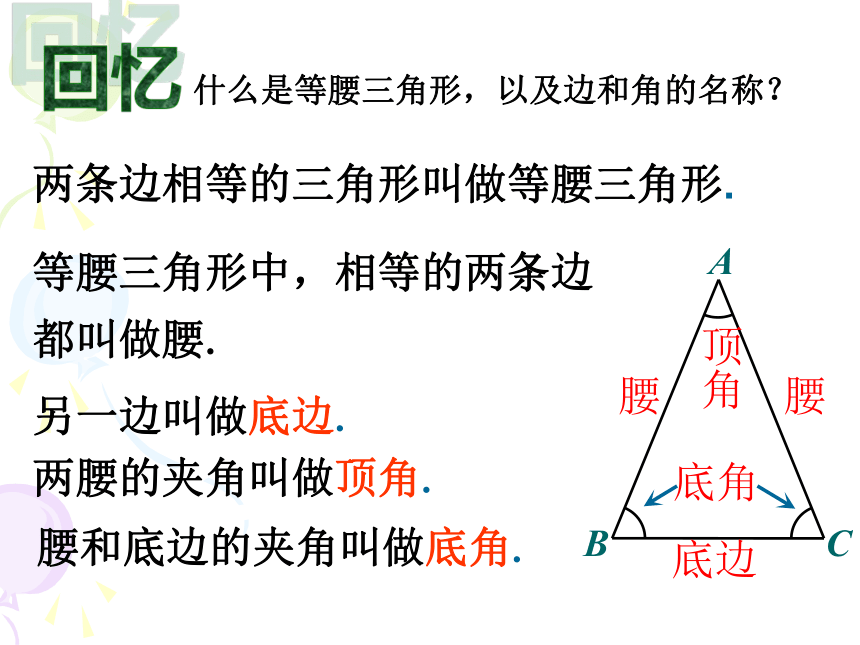
课件13张PPT。12.3.1等腰三角形的性质两条边相等的三角形叫做等腰三角形.等腰三角形中,相等的两条边都叫做腰.底边回忆两腰的夹角叫做顶角.另一边叫做底边.腰和底边的夹角叫做底角.什么是等腰三角形,以及边和角的名称?
活动1
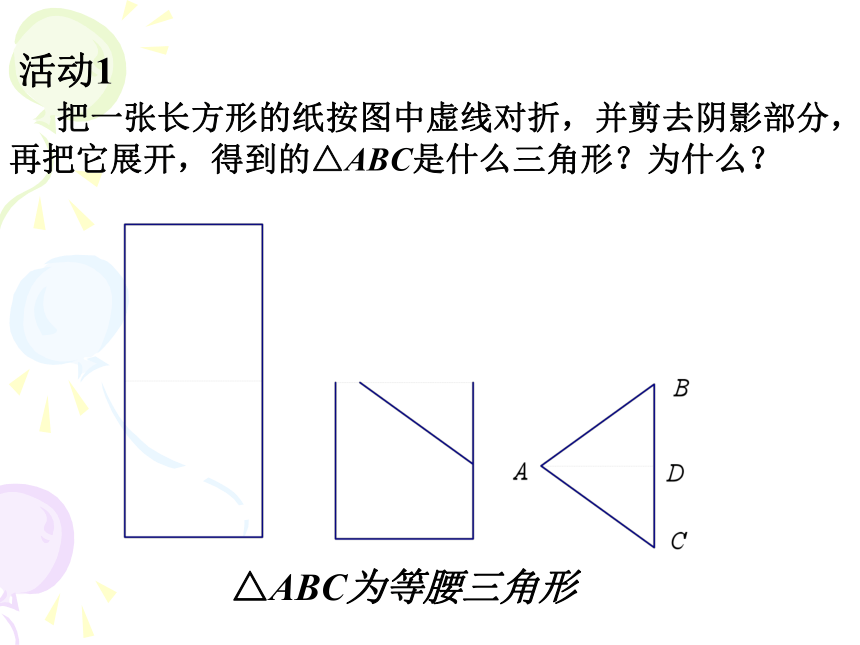
把一张长方形的纸按图中虚线对折,并剪去阴影部分,
再把它展开,得到的△ABC是什么三角形?为什么? △ABC为等腰三角形活动2
(1)活动1中剪出的等腰三角形是轴对称图形吗?为什么?对称轴是什么?
(2)把活动1中剪出的△ABC沿折痕AD对折,找出其中相等的线段和角,填入下表。 等腰三角形具备一般三角形的性质和两边相等。BD=DCAD=ADAB=AC∠B=∠C∠BAD=∠CAD∠ADB=∠ADC从上表中你能发现等腰三角形还具有什么性质吗?
说一说你的猜想。
猜想1:等腰三角形的两个底角相等。
(等角对等边)猜想2:等腰三角形顶角平分线、底边上
的中线、底边上的高互相重合(三线合一) 活动3 验证猜想 1.猜想1的条件和结论分别是什么?
条件是:等腰三角形
结论是:两个底角相
2.用数学符号如何表达条件和结论?
条件是:已知△ABC中,AB=AC。
结论是:求证:∠B=∠C;
3.如何证明?ABDC证法二
证明:过点A作∠BAC的平分线AD,与BC交于点D.∵AD平分∠BAC(已知)∴ ∠BAD= ∠CAD (角平分线的意义)在△ABD与△ACD中∴ △ABD≌△ACD (SAS)∴ ∠B= ∠ C(全等三角形的对应角相等)证法三
证明:过点A作AD⊥BC,垂足为D.∴ ∠BDA= ∠CDA=90°在RT△ABD与RT△ACD中∴ △ABD≌△ACD (HL)∴ ∠B= ∠ CADCB 受猜想1的证明的启发,你能证明猜想2吗?注:猜想2可以看成是由三个猜想合在一起组成的。
等腰三角形底边上的中线也是底边上的高和顶角平分线。
等腰三角形顶角平分线也是底边上的中线和底边上的高。
等腰三角形底边上的高也是顶角平分线和底边上的中线。猜想1:等腰三角形的两个底角相等。
(等角对等边)猜想2:等腰三角形顶角平分线、底边上
的中线、底边上的高互相重合。
(三线合一) 性质1:性质2:活动4
例1、如图,在△ABC中,AB=AC,点D在AC上,
且BD=BC=AD,求△ABC各个内角的度数.12图中有几个等腰三角形?
设∠A=x,用x表示∠1=______,∠2=_______,
∠C=______, ∠ABC=______.
求△ABC各个角的度数x2x2x2x△ABC, △ABD ,△BCD解:∵AB=AC,
∴∠ABC=∠C (等边对等角)
∵BD=BC,
∴ ∠C =∠2 (等边对等角)
∵ AD=BD
∴ ∠A=∠1 (等边对等角)
设∠A=x,则
∠2=∠A+∠1=2x,
从而∠ABC=∠C=∠2=2x.
于是在△ABC中,有∠ABC+∠C+∠A=180°
解得x=36°
在△ABC中,∠A=36° ∠ABC=∠C=72°12例2、在△ABC中,AB=AC,D为BC边
上的中点,DE⊥AB,DF⊥AC,垂足分
别是E,F.求证DE=DF.
证明:连接AD
∵AB=AC,D为BC边上的中点
∴AD为∠BAC的角平分线
(三线合一)
又∵DE⊥AB,DF⊥AC
∴DE=DF(角平分线性质定理)活动5
练习
填空: △ABC中,D在BC上,
(1) 如果AB=AC,那么____=____(等边对等角)
(2) 如果AB=AC ,AD⊥AC, 那么 _______=______,
_______ =______.
(3) 如果AB=AC ,∠BAD=∠CAD, 那么____⊥_____,
_____ =_____.
(4) 如果AB=AC, BD=DC, 那么_________=________,
_____⊥_____.
5、等腰三角形顶角是36°,另外两个角分别是多少___________。
6、等腰三角形一个角是70°,另外两个角分别是____________。
7、等腰三角形一个角是120°,另外两个角分别是___________。
ABCD∟∠CADBDBCBD∠CADAD∠BADCDADCD∠BADBC∠B∠C72°,72°55°,55°或70°,40°30°,30°注:等腰三角形的底角不可能是钝角,顶角可以是任意角。活动6:小结
这节课我们主要学习了什么内容?1、等腰三角形的两个性质及运用。2、等腰三角形中三条常见辅助线的做法。
活动1
把一张长方形的纸按图中虚线对折,并剪去阴影部分,
再把它展开,得到的△ABC是什么三角形?为什么? △ABC为等腰三角形活动2
(1)活动1中剪出的等腰三角形是轴对称图形吗?为什么?对称轴是什么?
(2)把活动1中剪出的△ABC沿折痕AD对折,找出其中相等的线段和角,填入下表。 等腰三角形具备一般三角形的性质和两边相等。BD=DCAD=ADAB=AC∠B=∠C∠BAD=∠CAD∠ADB=∠ADC从上表中你能发现等腰三角形还具有什么性质吗?
说一说你的猜想。
猜想1:等腰三角形的两个底角相等。
(等角对等边)猜想2:等腰三角形顶角平分线、底边上
的中线、底边上的高互相重合(三线合一) 活动3 验证猜想 1.猜想1的条件和结论分别是什么?
条件是:等腰三角形
结论是:两个底角相
2.用数学符号如何表达条件和结论?
条件是:已知△ABC中,AB=AC。
结论是:求证:∠B=∠C;
3.如何证明?ABDC证法二
证明:过点A作∠BAC的平分线AD,与BC交于点D.∵AD平分∠BAC(已知)∴ ∠BAD= ∠CAD (角平分线的意义)在△ABD与△ACD中∴ △ABD≌△ACD (SAS)∴ ∠B= ∠ C(全等三角形的对应角相等)证法三
证明:过点A作AD⊥BC,垂足为D.∴ ∠BDA= ∠CDA=90°在RT△ABD与RT△ACD中∴ △ABD≌△ACD (HL)∴ ∠B= ∠ CADCB 受猜想1的证明的启发,你能证明猜想2吗?注:猜想2可以看成是由三个猜想合在一起组成的。
等腰三角形底边上的中线也是底边上的高和顶角平分线。
等腰三角形顶角平分线也是底边上的中线和底边上的高。
等腰三角形底边上的高也是顶角平分线和底边上的中线。猜想1:等腰三角形的两个底角相等。
(等角对等边)猜想2:等腰三角形顶角平分线、底边上
的中线、底边上的高互相重合。
(三线合一) 性质1:性质2:活动4
例1、如图,在△ABC中,AB=AC,点D在AC上,
且BD=BC=AD,求△ABC各个内角的度数.12图中有几个等腰三角形?
设∠A=x,用x表示∠1=______,∠2=_______,
∠C=______, ∠ABC=______.
求△ABC各个角的度数x2x2x2x△ABC, △ABD ,△BCD解:∵AB=AC,
∴∠ABC=∠C (等边对等角)
∵BD=BC,
∴ ∠C =∠2 (等边对等角)
∵ AD=BD
∴ ∠A=∠1 (等边对等角)
设∠A=x,则
∠2=∠A+∠1=2x,
从而∠ABC=∠C=∠2=2x.
于是在△ABC中,有∠ABC+∠C+∠A=180°
解得x=36°
在△ABC中,∠A=36° ∠ABC=∠C=72°12例2、在△ABC中,AB=AC,D为BC边
上的中点,DE⊥AB,DF⊥AC,垂足分
别是E,F.求证DE=DF.
证明:连接AD
∵AB=AC,D为BC边上的中点
∴AD为∠BAC的角平分线
(三线合一)
又∵DE⊥AB,DF⊥AC
∴DE=DF(角平分线性质定理)活动5
练习
填空: △ABC中,D在BC上,
(1) 如果AB=AC,那么____=____(等边对等角)
(2) 如果AB=AC ,AD⊥AC, 那么 _______=______,
_______ =______.
(3) 如果AB=AC ,∠BAD=∠CAD, 那么____⊥_____,
_____ =_____.
(4) 如果AB=AC, BD=DC, 那么_________=________,
_____⊥_____.
5、等腰三角形顶角是36°,另外两个角分别是多少___________。
6、等腰三角形一个角是70°,另外两个角分别是____________。
7、等腰三角形一个角是120°,另外两个角分别是___________。
ABCD∟∠CADBDBCBD∠CADAD∠BADCDADCD∠BADBC∠B∠C72°,72°55°,55°或70°,40°30°,30°注:等腰三角形的底角不可能是钝角,顶角可以是任意角。活动6:小结
这节课我们主要学习了什么内容?1、等腰三角形的两个性质及运用。2、等腰三角形中三条常见辅助线的做法。
