沪科版数学九年级上册 22.3 相似三角形的性质教案
文档属性
| 名称 | 沪科版数学九年级上册 22.3 相似三角形的性质教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 93.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 00:00:00 | ||
图片预览

文档简介
22.3 相似三角形的性质(1)
●教学目标
(一)教学知识点
相似三角形对应高的比,对应角平分线的比和对应中线的比与相似比的关系.
(二)能力训练要求
1. 熟练应用相似三角形的性质:对应高的比、对应角平分线的比、对应中线的比都等于相似比。2.利用相似三角形的性质解决一些实际问题.
(三)情感与价值观要求
1.通过探索相似三角形中对应线段的比与相似比的关系,培养学生的探索精神和合作意识.2.通过运用相似三角形的性质,增强学生的应用意识.
●教学重点
1.相似三角形中对应线段比值的推导.2.运用相似三角形的性质解决实际问题.
●教学难点
相似三角形的性质的运用.
●教学方法:引导启发式
●教具准备
投影片两张
●教学过程
Ⅰ.创设问题情境,引入新课
[师]在前面我们学习了相似多边形的性质,知道相似多边形的对应角相等,对应边成比例,相似三角形是相似多边形中的一种,因此三对对应角相等,三对对应边成比例.那么,在两个相似三角形中是否只有对应角相等、对应边成比例这个性质呢?本节课我们将进行研究相似三角形的其他性质.
Ⅱ.新课讲解
1.做一做
投影片
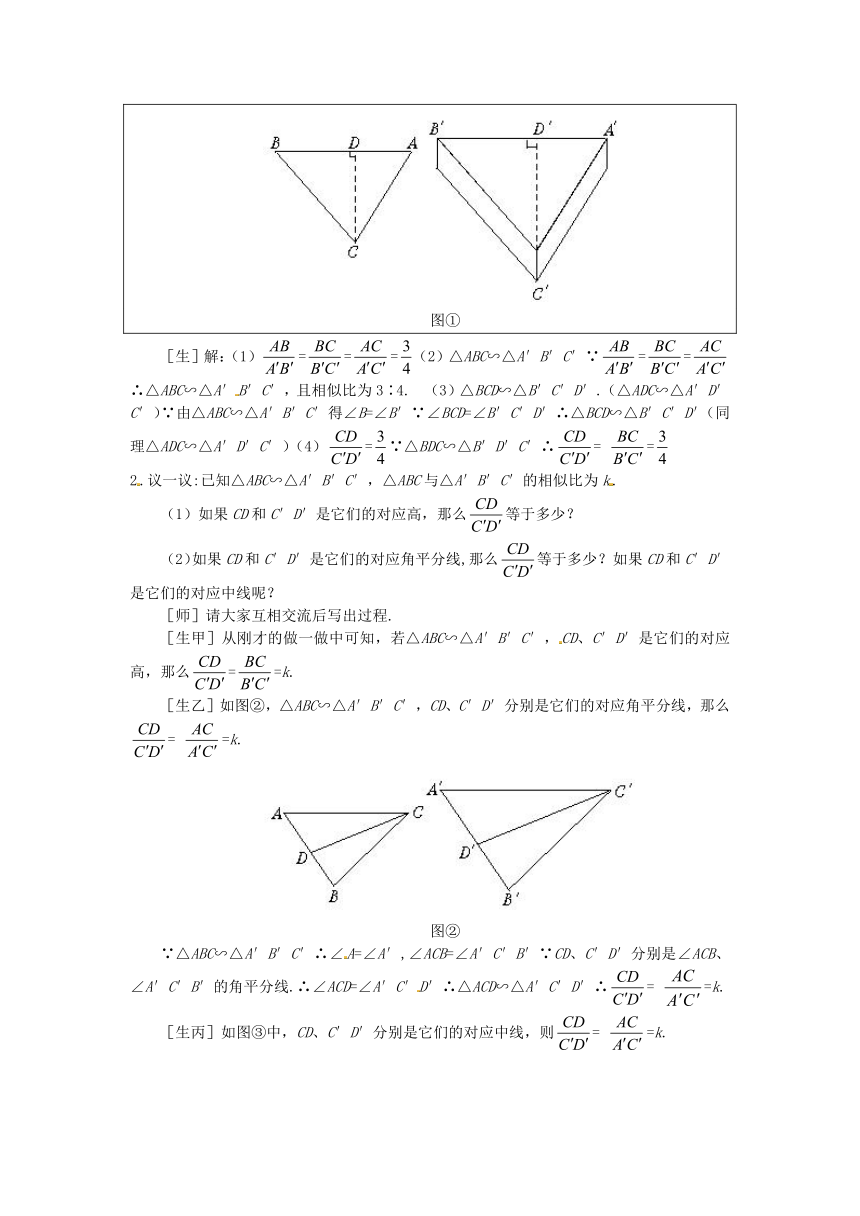
钳工小王准备按照比例尺为3∶4的图纸制作三角形零件,如图,图纸上的△ABC表示该零件的横断面△A′B′C′,CD和C′D′分别是它们的高.
(1),,各等于多少?
(2)△ABC与△A′B′C′相似吗?如果相似,请说明理由,并指出它们的相似比.
(3)请你在图①中再找出一对相似三角形.
(4)等于多少?你是怎么做的?与同伴交流.
图①
[生]解:(1)===(2)△ABC∽△A′B′C′∵==∴△ABC∽△A′B′C′,且相似比为3∶4. (3)△BCD∽△B′C′D′.(△ADC∽△A′D′C′)∵由△ABC∽△A′B′C′得∠B=∠B′∵∠BCD=∠B′C′D′∴△BCD∽△B′C′D′(同理△ADC∽△A′D′C′)(4)=∵△BDC∽△B′D′C′∴= =
2.议一议:已知△ABC∽△A′B′C′,△ABC与△A′B′C′的相似比为k.
(1)如果CD和C′D′是它们的对应高,那么等于多少?
(2)如果CD和C′D′是它们的对应角平分线,那么等于多少?如果CD和C′D′是它们的对应中线呢?
[师]请大家互相交流后写出过程.
[生甲]从刚才的做一做中可知,若△ABC∽△A′B′C′,CD、C′D′是它们的对应高,那么==k.
[生乙]如图②,△ABC∽△A′B′C′,CD、C′D′分别是它们的对应角平分线,那么= =k.
图②
∵△ABC∽△A′B′C′∴∠A=∠A′,∠ACB=∠A′C′B′∵CD、C′D′分别是∠ACB、∠A′C′B′的角平分线.∴∠ACD=∠A′C′D′∴△ACD∽△A′C′D′∴= =k.
[生丙]如图③中,CD、C′D′分别是它们的对应中线,则= =k.
图③
∵△ABC∽△A′B′C′∴∠A=∠A′,= =k.∵CD、C′D′分别是中线∴===k.∴△ACD∽△A′C′D′∴= =k.
由此可知相似三角形还有以下性质.相似三角形对应高的比、对应角平分线的比和对应中线的比都等于相似比.
3.例题讲解 (投影片)
图④
如图④所示,AD是△ABC的高,AD=h,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.当SR=BC时,求DE的长,如果SR=BC呢?
解:∵ SR⊥AD,BC⊥AD,∴SR∥BC.∵∠ASR=∠B, ∠ARS=∠C,
∴△ASR∽△ABC(两角分别相等的两个三角形相似).
∴(相似三角形对应高的比等于相似比),即.
当SR=BC时,得,解得DE=h
当SR=BC时,得,解得DE=h
Ⅲ.课堂练习
如果两个相似三角形对应高的比为4∶5,那么这两个相似三角形的相似比是多少?对应中线的比,对应角平分线的比呢?(都是4∶5).
Ⅳ.课时小结
本节课主要根据相似三角形的性质和判定推导出了相似三角形的性质:相似三角形的对应高的比、对应角平分线的比和对应中线的比都等于相似比.
Ⅴ.课后作业 完成习题 Ⅵ.活动与探索
图⑤
如图⑤,AD,A′D′分别是△ABC和△A′B′C′的角平分线,且
== 你认为△ABC∽△A′B′C′吗?
解:△ABC∽△A′B′C′成立.∵==∴△ABD∽△A′B′D′
∴∠B=∠B′,∠BAD=∠B′A′D′∵∠BAC=2∠BAD,∠B′A′C′=2∠B′A′D′
∴∠BAC=∠B′A′C′∴△ABC∽△A′B′C′
●板书设计
22.3相似三角形的性质(一)
一、1.做一做
2.议一议
3.例题讲解
二、课堂练习
三、课时小节
四、课后作业
●备课资料如图⑥,CD是Rt△ABC的斜边AB上的高.
(1)则图中有几对相似三角形.(2)若AD=9 cm,CD=6 cm,求BD.(3)若AB=25 cm,BC=15 cm,求BD.解:(1)∵CD⊥AB∴∠ADC=∠BDC=∠ACB=90° 在△ADC和 △ACB中 ∠ADC=∠ACB=90°∠A=∠A ∴△ADC∽△ACB同理可知,△CDB∽△ACB
图⑥
∴△ADC∽△CDB所以图中有三对相似三角形.
(2)∵△ACD∽△CBD∴即∴BD=4 (cm)(3)∵△CBD∽△ABC ∴.∴∴BD==9 (cm)
●教学目标
(一)教学知识点
相似三角形对应高的比,对应角平分线的比和对应中线的比与相似比的关系.
(二)能力训练要求
1. 熟练应用相似三角形的性质:对应高的比、对应角平分线的比、对应中线的比都等于相似比。2.利用相似三角形的性质解决一些实际问题.
(三)情感与价值观要求
1.通过探索相似三角形中对应线段的比与相似比的关系,培养学生的探索精神和合作意识.2.通过运用相似三角形的性质,增强学生的应用意识.
●教学重点
1.相似三角形中对应线段比值的推导.2.运用相似三角形的性质解决实际问题.
●教学难点
相似三角形的性质的运用.
●教学方法:引导启发式
●教具准备
投影片两张
●教学过程
Ⅰ.创设问题情境,引入新课
[师]在前面我们学习了相似多边形的性质,知道相似多边形的对应角相等,对应边成比例,相似三角形是相似多边形中的一种,因此三对对应角相等,三对对应边成比例.那么,在两个相似三角形中是否只有对应角相等、对应边成比例这个性质呢?本节课我们将进行研究相似三角形的其他性质.
Ⅱ.新课讲解
1.做一做
投影片
钳工小王准备按照比例尺为3∶4的图纸制作三角形零件,如图,图纸上的△ABC表示该零件的横断面△A′B′C′,CD和C′D′分别是它们的高.
(1),,各等于多少?
(2)△ABC与△A′B′C′相似吗?如果相似,请说明理由,并指出它们的相似比.
(3)请你在图①中再找出一对相似三角形.
(4)等于多少?你是怎么做的?与同伴交流.
图①
[生]解:(1)===(2)△ABC∽△A′B′C′∵==∴△ABC∽△A′B′C′,且相似比为3∶4. (3)△BCD∽△B′C′D′.(△ADC∽△A′D′C′)∵由△ABC∽△A′B′C′得∠B=∠B′∵∠BCD=∠B′C′D′∴△BCD∽△B′C′D′(同理△ADC∽△A′D′C′)(4)=∵△BDC∽△B′D′C′∴= =
2.议一议:已知△ABC∽△A′B′C′,△ABC与△A′B′C′的相似比为k.
(1)如果CD和C′D′是它们的对应高,那么等于多少?
(2)如果CD和C′D′是它们的对应角平分线,那么等于多少?如果CD和C′D′是它们的对应中线呢?
[师]请大家互相交流后写出过程.
[生甲]从刚才的做一做中可知,若△ABC∽△A′B′C′,CD、C′D′是它们的对应高,那么==k.
[生乙]如图②,△ABC∽△A′B′C′,CD、C′D′分别是它们的对应角平分线,那么= =k.
图②
∵△ABC∽△A′B′C′∴∠A=∠A′,∠ACB=∠A′C′B′∵CD、C′D′分别是∠ACB、∠A′C′B′的角平分线.∴∠ACD=∠A′C′D′∴△ACD∽△A′C′D′∴= =k.
[生丙]如图③中,CD、C′D′分别是它们的对应中线,则= =k.
图③
∵△ABC∽△A′B′C′∴∠A=∠A′,= =k.∵CD、C′D′分别是中线∴===k.∴△ACD∽△A′C′D′∴= =k.
由此可知相似三角形还有以下性质.相似三角形对应高的比、对应角平分线的比和对应中线的比都等于相似比.
3.例题讲解 (投影片)
图④
如图④所示,AD是△ABC的高,AD=h,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.当SR=BC时,求DE的长,如果SR=BC呢?
解:∵ SR⊥AD,BC⊥AD,∴SR∥BC.∵∠ASR=∠B, ∠ARS=∠C,
∴△ASR∽△ABC(两角分别相等的两个三角形相似).
∴(相似三角形对应高的比等于相似比),即.
当SR=BC时,得,解得DE=h
当SR=BC时,得,解得DE=h
Ⅲ.课堂练习
如果两个相似三角形对应高的比为4∶5,那么这两个相似三角形的相似比是多少?对应中线的比,对应角平分线的比呢?(都是4∶5).
Ⅳ.课时小结
本节课主要根据相似三角形的性质和判定推导出了相似三角形的性质:相似三角形的对应高的比、对应角平分线的比和对应中线的比都等于相似比.
Ⅴ.课后作业 完成习题 Ⅵ.活动与探索
图⑤
如图⑤,AD,A′D′分别是△ABC和△A′B′C′的角平分线,且
== 你认为△ABC∽△A′B′C′吗?
解:△ABC∽△A′B′C′成立.∵==∴△ABD∽△A′B′D′
∴∠B=∠B′,∠BAD=∠B′A′D′∵∠BAC=2∠BAD,∠B′A′C′=2∠B′A′D′
∴∠BAC=∠B′A′C′∴△ABC∽△A′B′C′
●板书设计
22.3相似三角形的性质(一)
一、1.做一做
2.议一议
3.例题讲解
二、课堂练习
三、课时小节
四、课后作业
●备课资料如图⑥,CD是Rt△ABC的斜边AB上的高.
(1)则图中有几对相似三角形.(2)若AD=9 cm,CD=6 cm,求BD.(3)若AB=25 cm,BC=15 cm,求BD.解:(1)∵CD⊥AB∴∠ADC=∠BDC=∠ACB=90° 在△ADC和 △ACB中 ∠ADC=∠ACB=90°∠A=∠A ∴△ADC∽△ACB同理可知,△CDB∽△ACB
图⑥
∴△ADC∽△CDB所以图中有三对相似三角形.
(2)∵△ACD∽△CBD∴即∴BD=4 (cm)(3)∵△CBD∽△ABC ∴.∴∴BD==9 (cm)
