沪科版数学九年级上册 23.1 锐角的三角函数课件(共26张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 23.1 锐角的三角函数课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 476.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 14:39:40 | ||
图片预览



文档简介
(共26张PPT)
锐角的三角函数
情境引入
我们都有过走上坡路的经验,坡面有陡有平,在数学上该如何衡量坡面的倾斜程度呢?如图所示:
100m
30m
100m
20m
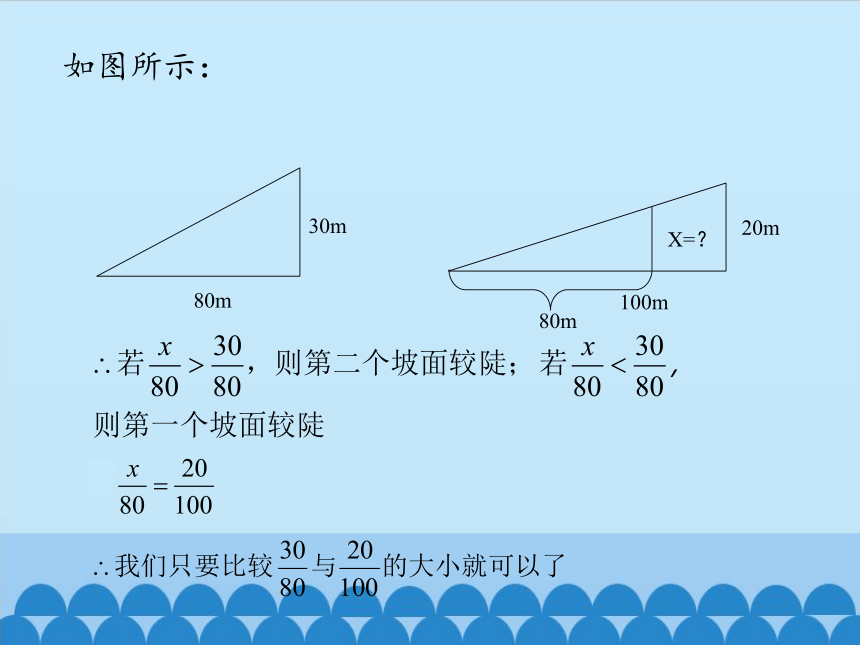
如图所示:
80m
30m
20m
100m
X=?
80m
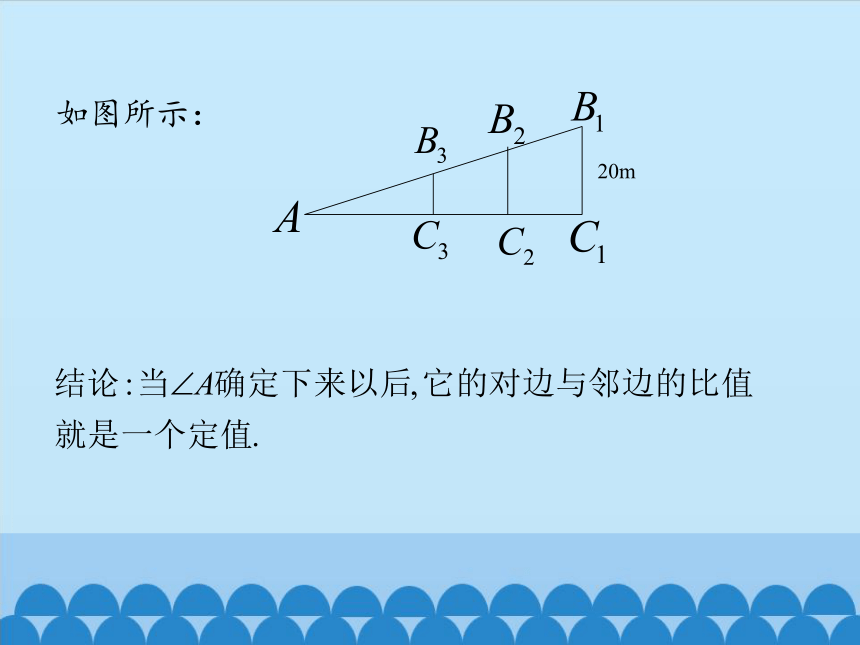
如图所示:
20m
动手实践,寻找规律
由推理可得:角度不变,比值不变;
由动态演示:角度改变,比值改变。
A
B
C
α
B’
C’
β
D
D
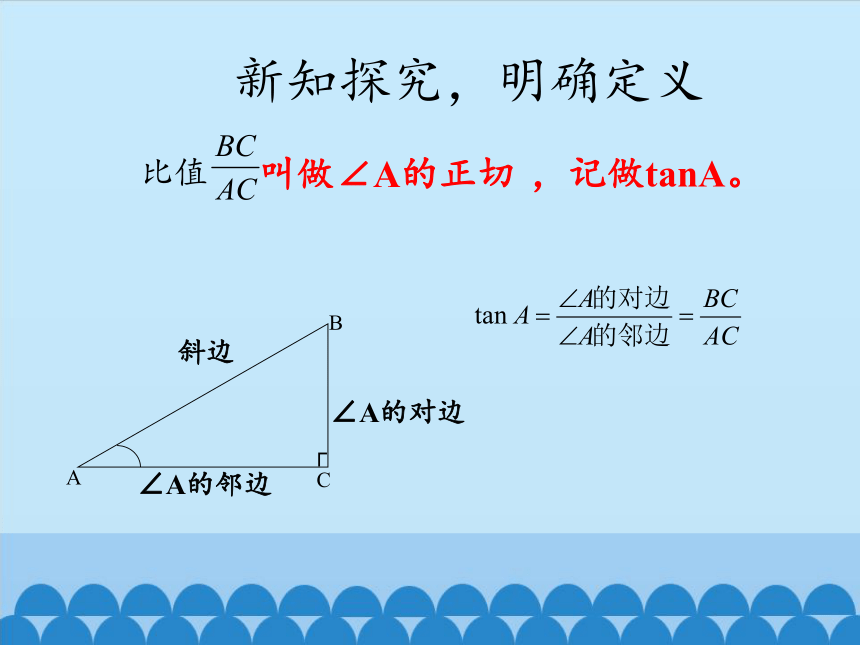
新知探究,明确定义
比值
叫做∠A的正切
,记做tanA。
┌
B
∠A的对边
C
∠A的邻边
A
斜边
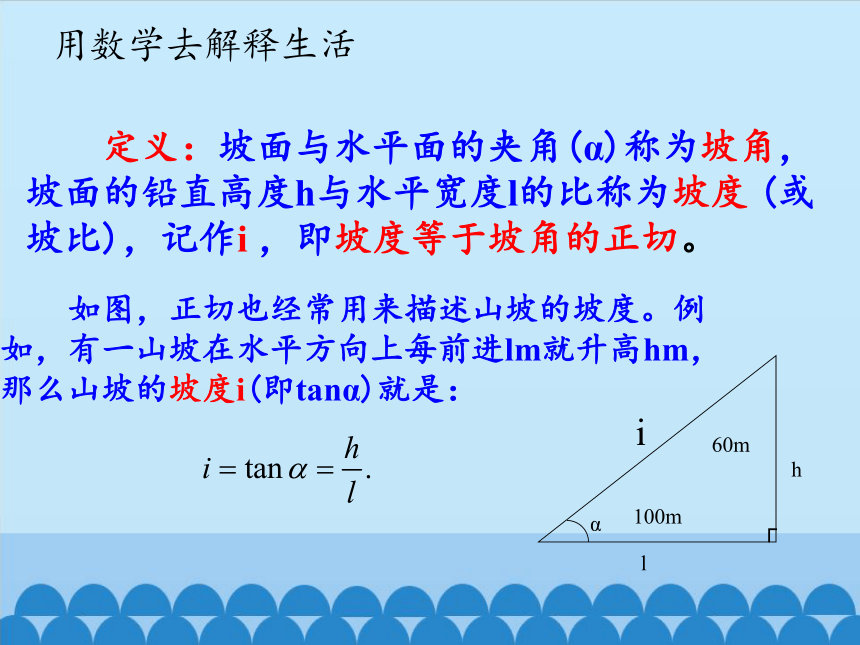
用数学去解释生活
如图,正切也经常用来描述山坡的坡度。例如,有一山坡在水平方向上每前进lm就升高hm,
那么山坡的坡度i(即tanα)就是:
定义:坡面与水平面的夹角(α)称为坡角,坡面的铅直高度h与水平宽度l的比称为坡度 (或坡比),记作i ,即坡度等于坡角的正切。
100m
60m
α
i
┌
h
l
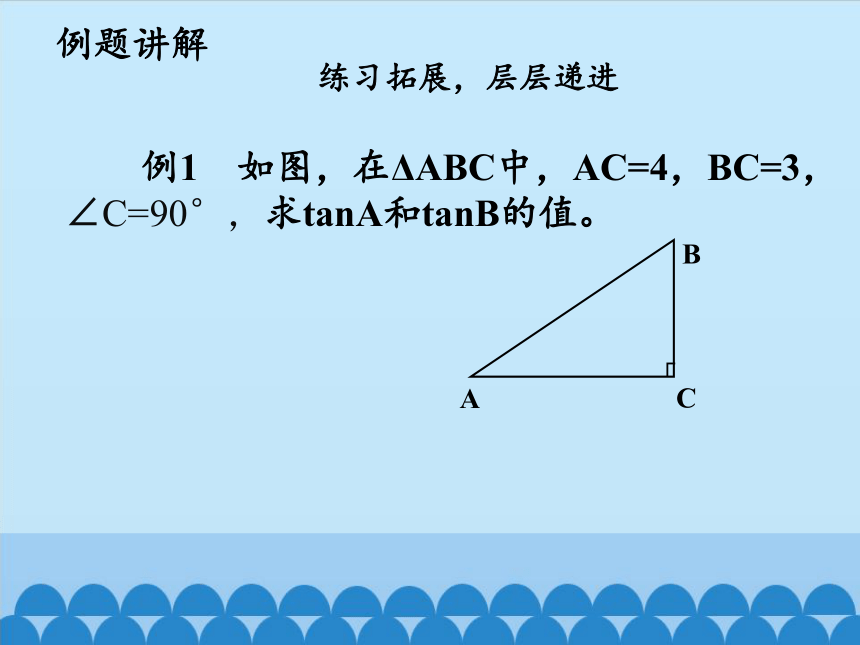
例题讲解
例1 如图,在ΔABC中,AC=4,BC=3,
∠C=90°,求tanA和tanB的值。
A
C
B
┌
练习拓展,层层递进
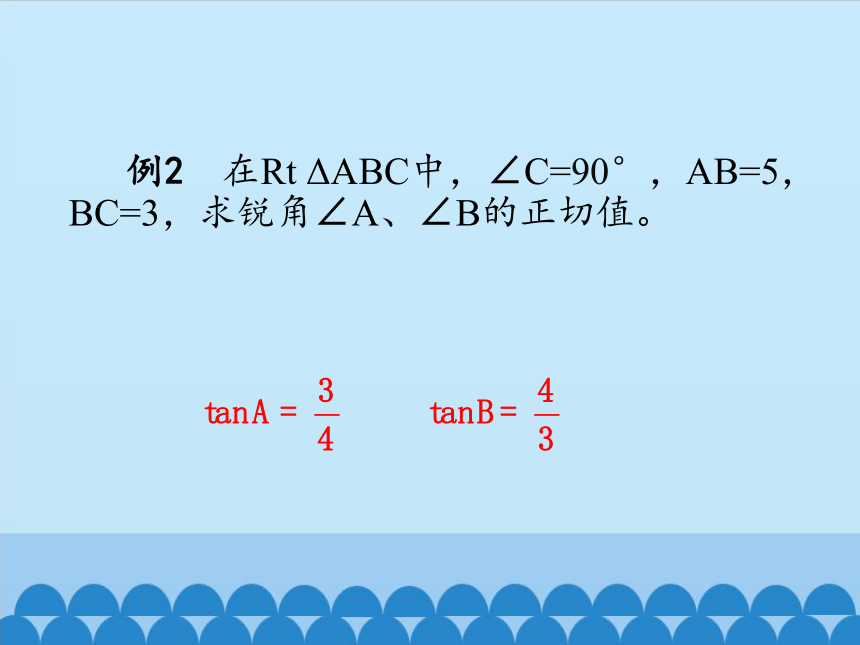
例2 在Rt ΔABC中,∠C=90°,AB=5,BC=3,求锐角∠A、∠B的正切值。
练一练
1.判断对错:
A
10m
6m
B
C
(1)如图,tanA= ( )
(2)tanB= ( )
(3)tanA=0.75m( )
(4)tanB=0.8( )
√
×
×
×
tanA是一个比值(注意比的顺序),无单位。
(5)如图,tanA= ( )
×
2.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,tanA的值( )
A、扩大100倍 B、缩小
C、不变 D、不能确定
C
练一练
小结:
1.正切的定义;
2.坡比的表示方法。
如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的正切,记作:tanA。
∠A的对边a
B
C
A
斜边c
∠A的邻边b
正切:
tanA=
=
tanB=
=
当直角三角形的一个锐角的大小确定时,其对边与斜边的比值,邻边与斜边的比值也是唯一确定的吗?
探究
也是定值吗?
如:∠A的对边与斜边的比值,邻边与斜边的比值
即: =
=
再探究
B
C
A
B'
C'
在任意Rt△ABC中,∠C=90°,在AB(或延长线)上任取一点B′,作B′C′垂直于AC,垂足为C′点,那么 与 有什么关系?你能解释一下吗?
由于∠ACB=∠C′=90°,所以BC//B′C′
所以Rt△ABC∽Rt△AB′C′
且为定值(常数)
在直角三角形中,锐角A的对边与斜边的比叫做角A的正弦,记作sinA。
类似地可以证明:在有一个锐角A的直角三角形中,角A的邻边与斜边的比值也为一个常数。
定义
在直角三角形中,锐角A的邻边与斜边的比叫做角A的余弦,记作cosA。
即:
即:
斜边
的邻边
角
A
A
=
cos
锐角A的正弦、
余弦、正切都叫做
∠A的锐角三角函数。
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数。同样地,cosA、tanA也是A的函数。
B
A
C
a
b
c
归纳小结
求∠A的各个三角函数值。
∠A的邻边是AC。根据勾股定理,得
于是AB=13m。
C
A
B
5m
12m
例题
解
思考
求∠B的sinB和cosB的值。
例1 在直角三角形ABC中,∠C=90 ,BC=5m,AC=12m。
在直角三角形ABC中,∠C=90 ,
BC∶AC=3∶4。
A
C
B
解
∠A的对边为BC=3k,斜边AB=5k,于是
求∠A的正弦sinA、余弦cosA。
因为BC∶AC=3∶4,
∠A的邻边是AC=4k,于是
拓展延伸
设BC=3k,AC=4k,根据勾股定理,得:AB=5k
方法点拨:
参数法(参数为k)
试一试
在直角三角形ABC中,∠C=90 ,∠A=30 。
求∠A的正弦sinA,
∠A的余弦cosA。
C
B
A
30°
解
Rt△ABC中,∠C=90 ,∠A=30 ,由于在
直角三角形中,30 所对的直角边等于斜边的一半,得:AB=2BC,即AB∶BC=2∶1。
设:BC=k,AB=2k
根据勾股定理,得:AC=
所以
例2 如图平面直角坐标系中,点P的坐标为(3,4),求OP与x轴正半轴夹角α的所有三角函数值。
α
y
Q
P(3,4)
x
O
过P作PQ⊥x轴于Q点,
例题
解
在Rt△POQ中,OQ=3,QP=4,所以OP=5。
所以
构造直角三角形
思路点拨:
展示你的风采
1.求直线y=2x与x轴正半轴夹角α的所有三角函数值。
解
o
x
y
y=2x
Q
P
在y=2x上任取一点P(1,2),过P作PQ⊥x轴于Q点,
在Rt△POQ中,OQ=1,QP=2,所以OP=
所以,
思考:求直线y=2x+2与x轴正半轴夹角α的所有三角函数值。
α
在直角三角形中,∠A为其中一个锐角
小结
这节课我们主要学习了哪些知识?有何体会和收获?有哪些你认为最重要?
斜边
∠A的邻边
A
=
cos
tanA=
其中sinA,cosA,tanA是关于角A的函数。
在锐角三角函数定义中有哪些注意事项?
定义中应该注意的几个问题:
回味无穷
1.sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2.sinA、cosA、tanA是一个比值(数值)。
3.sinA、cosA、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。
作业
发散思维
1.在等腰△ABC中,AB=AC=5,BC=6,求sinB,cosB,tanB。
A
B
C
谢 谢
锐角的三角函数
情境引入
我们都有过走上坡路的经验,坡面有陡有平,在数学上该如何衡量坡面的倾斜程度呢?如图所示:
100m
30m
100m
20m
如图所示:
80m
30m
20m
100m
X=?
80m
如图所示:
20m
动手实践,寻找规律
由推理可得:角度不变,比值不变;
由动态演示:角度改变,比值改变。
A
B
C
α
B’
C’
β
D
D
新知探究,明确定义
比值
叫做∠A的正切
,记做tanA。
┌
B
∠A的对边
C
∠A的邻边
A
斜边
用数学去解释生活
如图,正切也经常用来描述山坡的坡度。例如,有一山坡在水平方向上每前进lm就升高hm,
那么山坡的坡度i(即tanα)就是:
定义:坡面与水平面的夹角(α)称为坡角,坡面的铅直高度h与水平宽度l的比称为坡度 (或坡比),记作i ,即坡度等于坡角的正切。
100m
60m
α
i
┌
h
l
例题讲解
例1 如图,在ΔABC中,AC=4,BC=3,
∠C=90°,求tanA和tanB的值。
A
C
B
┌
练习拓展,层层递进
例2 在Rt ΔABC中,∠C=90°,AB=5,BC=3,求锐角∠A、∠B的正切值。
练一练
1.判断对错:
A
10m
6m
B
C
(1)如图,tanA= ( )
(2)tanB= ( )
(3)tanA=0.75m( )
(4)tanB=0.8( )
√
×
×
×
tanA是一个比值(注意比的顺序),无单位。
(5)如图,tanA= ( )
×
2.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,tanA的值( )
A、扩大100倍 B、缩小
C、不变 D、不能确定
C
练一练
小结:
1.正切的定义;
2.坡比的表示方法。
如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与邻边的比叫做∠A的正切,记作:tanA。
∠A的对边a
B
C
A
斜边c
∠A的邻边b
正切:
tanA=
=
tanB=
=
当直角三角形的一个锐角的大小确定时,其对边与斜边的比值,邻边与斜边的比值也是唯一确定的吗?
探究
也是定值吗?
如:∠A的对边与斜边的比值,邻边与斜边的比值
即: =
=
再探究
B
C
A
B'
C'
在任意Rt△ABC中,∠C=90°,在AB(或延长线)上任取一点B′,作B′C′垂直于AC,垂足为C′点,那么 与 有什么关系?你能解释一下吗?
由于∠ACB=∠C′=90°,所以BC//B′C′
所以Rt△ABC∽Rt△AB′C′
且为定值(常数)
在直角三角形中,锐角A的对边与斜边的比叫做角A的正弦,记作sinA。
类似地可以证明:在有一个锐角A的直角三角形中,角A的邻边与斜边的比值也为一个常数。
定义
在直角三角形中,锐角A的邻边与斜边的比叫做角A的余弦,记作cosA。
即:
即:
斜边
的邻边
角
A
A
=
cos
锐角A的正弦、
余弦、正切都叫做
∠A的锐角三角函数。
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数。同样地,cosA、tanA也是A的函数。
B
A
C
a
b
c
归纳小结
求∠A的各个三角函数值。
∠A的邻边是AC。根据勾股定理,得
于是AB=13m。
C
A
B
5m
12m
例题
解
思考
求∠B的sinB和cosB的值。
例1 在直角三角形ABC中,∠C=90 ,BC=5m,AC=12m。
在直角三角形ABC中,∠C=90 ,
BC∶AC=3∶4。
A
C
B
解
∠A的对边为BC=3k,斜边AB=5k,于是
求∠A的正弦sinA、余弦cosA。
因为BC∶AC=3∶4,
∠A的邻边是AC=4k,于是
拓展延伸
设BC=3k,AC=4k,根据勾股定理,得:AB=5k
方法点拨:
参数法(参数为k)
试一试
在直角三角形ABC中,∠C=90 ,∠A=30 。
求∠A的正弦sinA,
∠A的余弦cosA。
C
B
A
30°
解
Rt△ABC中,∠C=90 ,∠A=30 ,由于在
直角三角形中,30 所对的直角边等于斜边的一半,得:AB=2BC,即AB∶BC=2∶1。
设:BC=k,AB=2k
根据勾股定理,得:AC=
所以
例2 如图平面直角坐标系中,点P的坐标为(3,4),求OP与x轴正半轴夹角α的所有三角函数值。
α
y
Q
P(3,4)
x
O
过P作PQ⊥x轴于Q点,
例题
解
在Rt△POQ中,OQ=3,QP=4,所以OP=5。
所以
构造直角三角形
思路点拨:
展示你的风采
1.求直线y=2x与x轴正半轴夹角α的所有三角函数值。
解
o
x
y
y=2x
Q
P
在y=2x上任取一点P(1,2),过P作PQ⊥x轴于Q点,
在Rt△POQ中,OQ=1,QP=2,所以OP=
所以,
思考:求直线y=2x+2与x轴正半轴夹角α的所有三角函数值。
α
在直角三角形中,∠A为其中一个锐角
小结
这节课我们主要学习了哪些知识?有何体会和收获?有哪些你认为最重要?
斜边
∠A的邻边
A
=
cos
tanA=
其中sinA,cosA,tanA是关于角A的函数。
在锐角三角函数定义中有哪些注意事项?
定义中应该注意的几个问题:
回味无穷
1.sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2.sinA、cosA、tanA是一个比值(数值)。
3.sinA、cosA、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。
作业
发散思维
1.在等腰△ABC中,AB=AC=5,BC=6,求sinB,cosB,tanB。
A
B
C
谢 谢
