2021-2022学年苏科版八年级数学上册6.5一次函数与二元一次方程 同步强化训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册6.5一次函数与二元一次方程 同步强化训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 00:00:00 | ||
图片预览




文档简介
2021-2022学年苏科版八年级数学上
《6.5一次函数与二元一次方程》同步强化训练
(时间:100分钟 满分:120分)
一.选择题(每小题2分 共40分)
1.若直线y=kx+b的图象经过点(1,3),则方程kx+b=3的解是x=( )
A.1 B.2 C.3 D.4
2.已知直线y=kx+b经过点(k,3)和(1,k),则k的值为( )
A. B.± C. D.±
3.如图中的两直线l1,l2的交点坐标可以看作哪个方程组的解( )
A. B. C. D.
4.若三点(1,4),(2,7),(a,10)在同一直线上,则a的值为( )
A.-1 B.0 C.3 D.4
5.若方程组没有解,则一次函数y=1-x与y=-x的图象必定( )
A.重合 B.平行C.相交 D.无法判断
6.若以二元一次方程x+2y﹣b=0的解为坐标的点(x,y)都在直线y=﹣x+b﹣1上,则常数b=( )
A. B.2 C.﹣1 D.1
7.已知一次函数y1=2x+m与y2=2x+n(m≠n)的图象如图所示,则关于x与y的二元一次方程组的解的个数为( )
A.0个 B.1个 C.2个 D.无数个
第7题图 第8题图 第9题图 第10题图 第12题图
8.如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组的解为( )
A. B. C. D.
9.如图,过点Q(0,3)的一次函数与正比例函数y=2x的图象交于点P,能表示这个一次函数图象的方程是( )
A.3x﹣2y+3=0 B.3x﹣2y﹣3=0 C.x﹣y+3=0 D.x+y﹣3=0
10.如图中的两直线l1、l2的交点坐标可以看作哪个方程组的解( )
A. B. C. D.
11.已知和是二元一次方程ax+by+3=0的两个解,则一次函数y=ax+b(a≠0)的解析式为( )
A.y=﹣2x﹣3 B. C.y=﹣9x+3 D.
12.图中两直线l1、l2的交点坐标可以看作方程组( )的解.
A. B. C. D.
13.已知直线y=2x与y=﹣x+b的交点的坐标为(1,a),则方程组的解是( )
A. B. C. D.
14.图中两条直线l1和l2的交点坐标可以看作下列方程组( )中的解.
A. B. C. D.
第14题图 第15题图 第17题图 第18题图 第19题图
15.用图象法解二元一次方程组时,小英所画图象如图,则方程组的解为( )
A. B. C. D.
16.一次函数y=﹣2x+3的图象和y=kx﹣b的图象相交于点A(m,1),则关于x,y的二元一次方程组的解为( )
A. B. C. D.
17.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组的解是( )
A. B. C. D.
18.如图一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组的解为( )
A. B. C. D.
19.某公司准备与汽车租赁公司签订租车合同,以每月用车路程x km计算,甲汽车租赁公司每月收取的租赁费为y1元,乙汽车租赁公司每月收取的租赁费为y2元,若y1,y2与x之间的函数关系如图其中x=0对应的函数值为月固定租赁费,则下列判断错误的是( )
A.当月用车路程为2 000 km时,两家汽车租赁公司租赁费用相同
B.当月用车路程为2 300 km时,租赁乙汽车租赁公司的车比较合算
C.除去月固定租赁费,甲租赁公司每公里收取的费用比乙租赁公司多
D.甲租赁公司平均每公里收取的费用比乙租赁公司少
20.已知直线l1:y=-3x+b与直线l2:y=-kx+1在同一平面直角坐标系中的图象相交于点(1,-2),那么方程组的解是( )
A. B. C. D.
二、填空题(每小题2分 共20分)
21.直线y=kx+3与y=-x+3的图象如图3所示,则方程组的解为____.
第21题图 第22题图 第23题图 第24题图
22.一次函数y=2x-3与y=-x+1的图象的交点坐标为______.
23.如图,直线y=x+b与直线y=kx+6相交于点P(3,5),则关于x的不等式x+b>kx+6的解是__x>3__.
24.如图,观察图象,回答问题:(1)点A的横坐标是方程_____________的解.
(2)点C的横、纵坐标是方程组___________________的解.
25.无论m取何实数,直线y=x+3m与y=-x+1的交点不可能在第______象限.
26.如图,已知A,B,C,D是平面坐标系中坐标轴上的点,且△AOB≌△COD.设直线AB的函数表达式为y1=k1x+b1,直线CD的函数表达式为y2=k2x+b2,则k1·k2=___.
第26题图 第27题图 第28题图 第29题图 第30题图
27.如图,在平面直角坐标系中,四边形ABCO是正方形,点B的坐标为(4,4),直线y=mx-2恰好把正方形ABCO的面积分成相等的两部分,则m= .
28元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路程s关于行走时间t的函数图象,则两图象交点P的坐标是 .
29.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).不解关于x、y的方程组直接写出它的解___________;
30.如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是________.
三.解答题(60分)
31.(6分)如图,在平面直角坐标系xOy中,过点A(-6,0)的直线l1与直线l2:y=2x相交于点B(m,4).
(1)求直线l1的函数表达式.
(2)过动点P(n,0)且垂直于x轴的直线与l1,l2的交点分别为C,D.当点C位于点D上方时,求n的取值范围.
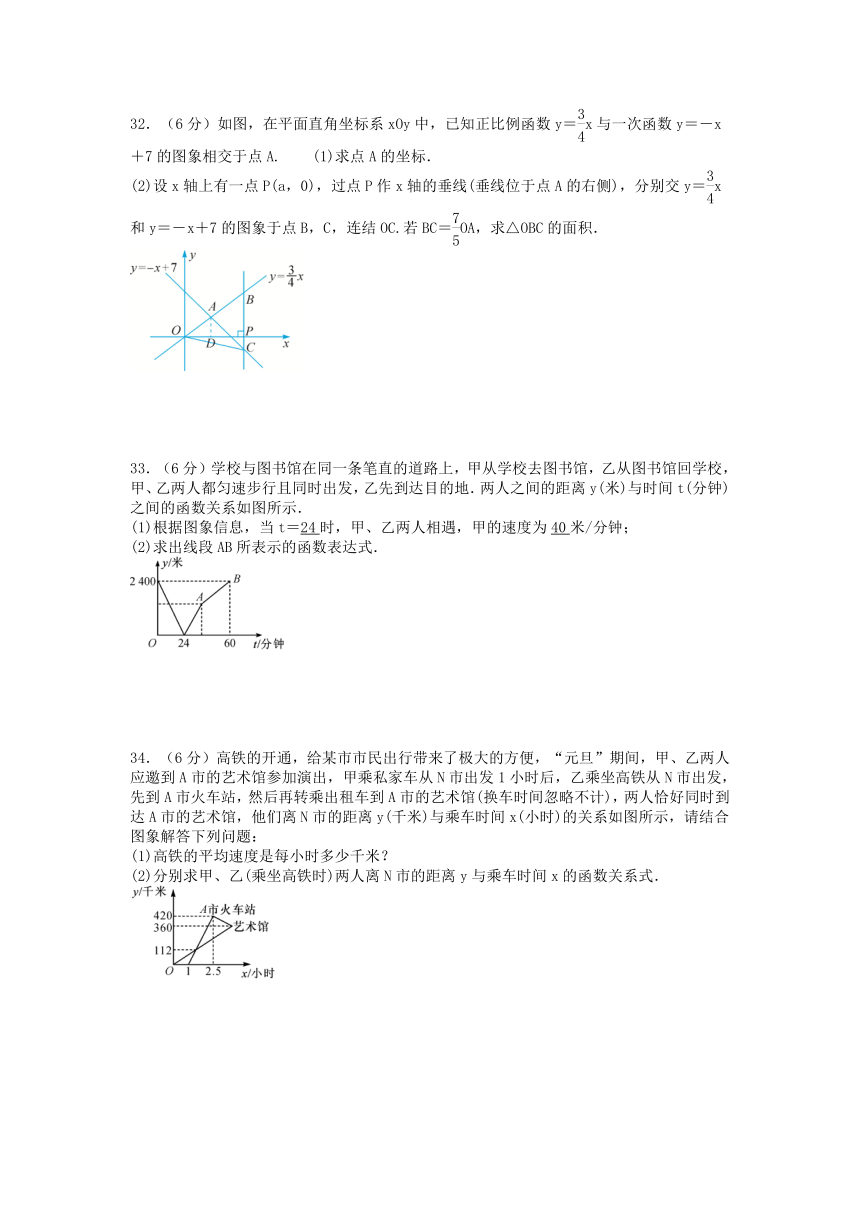
32.(6分)如图,在平面直角坐标系xOy中,已知正比例函数y=x与一次函数y=-x+7的图象相交于点A. (1)求点A的坐标.
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y=x和y=-x+7的图象于点B,C,连结OC.若BC=OA,求△OBC的面积.
33.(6分)学校与图书馆在同一条笔直的道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
(1)根据图象信息,当t=24时,甲、乙两人相遇,甲的速度为40米/分钟;
(2)求出线段AB所表示的函数表达式.
34.(6分)高铁的开通,给某市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题:
(1)高铁的平均速度是每小时多少千米?
(2)分别求甲、乙(乘坐高铁时)两人离N市的距离y与乘车时间x的函数关系式.
35.(9分)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2 000 kg~5 000 kg(含2 000 kg和5 000 kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货;
方案B:每千克5元,客户需支付运费2 000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(单位:元)与购买量x(单位:kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20 000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.
36.(9分)在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)的关系如图所示.请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是_____cm,_______cm,从点燃到燃尽所用的时间分别是_____h,_______h.
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数表达式.
(3)当x为何值时,甲、乙两根蜡烛在燃烧过程中的高度相等?
37.(9分)如图,在平面直角坐标系中,正方形OABC的一个顶点为B(1,1),点A,C分别在x轴,y轴上.
(1)点A的坐标为________,点C的坐标为________.
(2)判断直线y=-2x+与正方形OABC是否有交点,并说明理由.
(3)将直线y=-2x+进行平移,恰好能把正方形OABC分成面积相等的两部分,请求出平移后的直线的函数表达式.
38.(9分)某物流公司的快递车和货车每天往返于A,B两地,快递车比货车多往返一趟.下图表示快递车距离A地的路程y(km)与所用时间x(h)的函数图象.已知货车比快递车早1 h出发,到达B地后用2 h装卸货物,然后按原路、原速返回,结果比快递车最后一次返回A地晚1 h.
(1)请在图中画出货车距离A地的路程y(km)与所用时间x(h)的函数图象.
(2)求两车在途中相遇的次数(直接写出答案).
(3)求两车最后一次相遇时,距离A地的路程和货车从A地出发了几小时.
教师样卷
一.选择题(每小题2分 共40分)
1.若直线y=kx+b的图象经过点(1,3),则方程kx+b=3的解是x=( A )
A.1 B.2 C.3 D.4
2.已知直线y=kx+b经过点(k,3)和(1,k),则k的值为(B)
A. B.± C. D.±
3.如图中的两直线l1,l2的交点坐标可以看作哪个方程组的解(A)
A. B. C. D.
4.若三点(1,4),(2,7),(a,10)在同一直线上,则a的值为(C)
A.-1 B.0 C.3 D.4
5.若方程组没有解,则一次函数y=1-x与y=-x的图象必定(B)
A.重合 B.平行C.相交 D.无法判断
6.若以二元一次方程x+2y﹣b=0的解为坐标的点(x,y)都在直线y=﹣x+b﹣1上,则常数b=( B )
A. B.2 C.﹣1 D.1
7.已知一次函数y1=2x+m与y2=2x+n(m≠n)的图象如图所示,则关于x与y的二元一次方程组的解的个数为( A )
A.0个 B.1个 C.2个 D.无数个
第7题图 第8题图 第9题图 第10题图 第12题图
8.如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组的解为( A )
A. B. C. D.
9.如图,过点Q(0,3)的一次函数与正比例函数y=2x的图象交于点P,能表示这个一次函数图象的方程是( D )
A.3x﹣2y+3=0 B.3x﹣2y﹣3=0 C.x﹣y+3=0 D.x+y﹣3=0
10.如图中的两直线l1、l2的交点坐标可以看作哪个方程组的解( A )
A. B. C. D.
11.已知和是二元一次方程ax+by+3=0的两个解,则一次函数y=ax+b(a≠0)的解析式为( D )
A.y=﹣2x﹣3 B. C.y=﹣9x+3 D.
12.图中两直线l1、l2的交点坐标可以看作方程组( B )的解.
A. B. C. D.
13.已知直线y=2x与y=﹣x+b的交点的坐标为(1,a),则方程组的解是( A )
A. B. C. D.
14.图中两条直线l1和l2的交点坐标可以看作下列方程组( D )中的解.
A. B. C. D.
第14题图 第15题图 第17题图 第18题图 第19题图
15.用图象法解二元一次方程组时,小英所画图象如图,则方程组的解为( D )
A. B. C. D.
16.一次函数y=﹣2x+3的图象和y=kx﹣b的图象相交于点A(m,1),则关于x,y的二元一次方程组的解为( C )
A. B. C. D.
17.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组的解是( A )
A. B. C. D.
18.如图一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组的解为( A )
A. B. C. D.
19.某公司准备与汽车租赁公司签订租车合同,以每月用车路程x km计算,甲汽车租赁公司每月收取的租赁费为y1元,乙汽车租赁公司每月收取的租赁费为y2元,若y1,y2与x之间的函数关系如图其中x=0对应的函数值为月固定租赁费,则下列判断错误的是( D )
A.当月用车路程为2 000 km时,两家汽车租赁公司租赁费用相同
B.当月用车路程为2 300 km时,租赁乙汽车租赁公司的车比较合算
C.除去月固定租赁费,甲租赁公司每公里收取的费用比乙租赁公司多
D.甲租赁公司平均每公里收取的费用比乙租赁公司少
【解析】 A.交点为(2 000,2 000),那么当月用车路程为2 000 km,两家汽车租赁公司租赁费用相同,说法正确,不符合题意;B.由图象可得超过2 000 km时,相同路程,乙公司收费便宜,∴租赁乙汽车租赁公司车比较合算,说法正确,不符合题意;C.由图象易得乙的租赁费较高,当行驶2 000 km时,总收费相同,那么可得甲租赁公司每公里收取的费用比乙租赁公司多,说法正确,不符合题意;D.由图象可得平均每公里收费与路程有关,故该说法错误,符合题意,故选D.
20.已知直线l1:y=-3x+b与直线l2:y=-kx+1在同一平面直角坐标系中的图象相交于点(1,-2),那么方程组的解是(A)
A. B. C. D.
二、填空题(每小题2分 共20分)
21.直线y=kx+3与y=-x+3的图象如图3所示,则方程组的解为____.
第21题图 第22题图 第23题图 第24题图
22.一次函数y=2x-3与y=-x+1的图象的交点坐标为_(,- )_____.
23.如图,直线y=x+b与直线y=kx+6相交于点P(3,5),则关于x的不等式x+b>kx+6的解是__x>3__.
24.如图,观察图象,回答问题:(1)点A的横坐标是方程k1x+b1=0的解.
(2)点C的横、纵坐标是方程组的解.
25.无论m取何实数,直线y=x+3m与y=-x+1的交点不可能在第___三_____象限.
【解析】因为一次函数y=-x+1的图象经过一、二、四象限,所以,交点不会在第三象限.
26.如图,已知A,B,C,D是平面坐标系中坐标轴上的点,且△AOB≌△COD.设直线AB的函数表达式为y1=k1x+b1,直线CD的函数表达式为y2=k2x+b2,则k1·k2=__1__.
【解】 设点A(0,a),B(b,0),则OA=a,OB=-b.∵△AOB≌△COD,∴OC=a,OD=-b.∴点C(a,0),D(0,b).∵直线AB过点A,B,∴∴k1=-.同理可得k2=-,∴k1·k2=1.
第26题图 第27题图 第28题图 第29题图 第30题图
27.如图,在平面直角坐标系中,四边形ABCO是正方形,点B的坐标为(4,4),直线y=mx-2恰好把正方形ABCO的面积分成相等的两部分,则m= 2 .
28元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路程s关于行走时间t的函数图象,则两图象交点P的坐标是 (32,480) .
29.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).不解关于x、y的方程组直接写出它的解___________;
30.如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是________.
【答案】. 【解析】两个一次函数的交点坐标(-4,-2)即为方程组的解,即.
三.解答题(60分)
31.(6分)如图,在平面直角坐标系xOy中,过点A(-6,0)的直线l1与直线l2:y=2x相交于点B(m,4).
(1)求直线l1的函数表达式.
(2)过动点P(n,0)且垂直于x轴的直线与l1,l2的交点分别为C,D.当点C位于点D上方时,求n的取值范围.
【解】 (1)把点B(m,4)的坐标代入直线l2:y=2x,得m=2,即点B的坐标为(2,4).
设直线l2的函数表达式为y=kx+b(k≠0).由A,B两点均在直线l1上,得
解得则直线l1的函数表达式为y=x+3.
(2)由题意,得点C,D(n,2n).∵点C在点D的上方,∴+3>2n,解得n<2.
32.(6分)如图,在平面直角坐标系xOy中,已知正比例函数y=x与一次函数y=-x+7的图象相交于点A.
(1)求点A的坐标.
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y=x和y=-x+7的图象于点B,C,连结OC.若BC=OA,求△OBC的面积.
【解】 (1)联立解得∴点A(4,3).
(2)过点A作x轴的垂线,垂足为D.在Rt△OAD中,由勾股定理,得OA===5,∴BC=OA=×5=7.∵点P(a,0),∴点B,C(a,-a+7),∴BC=a-(-a+7)=a-7.∴a-7=7,解得a=8.∴S△OBC=BC·OP=×7×8=28.
33.(6分)学校与图书馆在同一条笔直的道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
(1)根据图象信息,当t=24时,甲、乙两人相遇,甲的速度为40米/分钟;
(2)求出线段AB所表示的函数表达式.
解:因为t=24时甲、乙两人相遇,所以甲、乙两人的速度和为2 400÷24=100(米/分钟).
所以乙的速度为100-40=60(米/分钟).
乙从图书馆回学校的时间为2 400÷60=40(分钟).
100×(40-24)=1 600,
所以A点的坐标为(40,1 600).
设线段AB所表示的函数表达式为y=kt+b,
因为A(40,1 600),B(60,2 400),
所以解得
所以线段AB所表示的函数表达式为y=40t(40≤t≤60).
34.(6分)高铁的开通,给某市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题:
(1)高铁的平均速度是每小时多少千米?
(2)分别求甲、乙(乘坐高铁时)两人离N市的距离y与乘车时间x的函数关系式.
解:(1)420÷(2.5-1)=280(千米/小时).
答:高铁的平均速度是每小时280千米.
(2)设甲离N市的距离y与乘车时间x的函数关系式为y甲=kx(k≠0),乙(乘坐高铁时)离N市的距离y与乘车时间x的函数关系式为y乙=mx+n(m≠0).
将点(1,0),(2.5,420)代入y乙=mx+n,得
解得
所以乙(乘坐高铁时)离N市的距离y与乘车时间x的函数关系式为y乙=280x-280(1≤x≤2.5).
当y乙=112时,280x-280=112,解得x=1.4.
将(1.4,112)代入y甲=kx,得
1.4k=112,解得k=80,
所以甲离N市的距离y与乘车时间x的函数关系式为y甲=80x.
35.(9分)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2 000 kg~5 000 kg(含2 000 kg和5 000 kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货;
方案B:每千克5元,客户需支付运费2 000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(单位:元)与购买量x(单位:kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20 000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.
解:(1)方案A:函数表达式为y=5.8x.方案B:函数表达式为y=5x+2 000;
(2)由题意,得5.8x<5x+2 000,解得x<2 500, ∴当购买量x的取值范围为2 000≤x<2 500时,选用方案A比方案B付款少;
(3)他应选择方案B.
36.(9分)在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)的关系如图所示.请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是30_cm,25_cm,从点燃到燃尽所用的时间分别是2_h,2.5_h.
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数表达式.
(3)当x为何值时,甲、乙两根蜡烛在燃烧过程中的高度相等?
【解】 (2)设甲蜡烛燃烧时y与x之间的函数表达式为y=k1x+b1.由图可知,函数的图象过点(2,0),(0,30),∴解得∴y=-15x+30.
设乙蜡烛燃烧时y与x之间的函数表达式为y=k2x+b2.由图可知,函数的图象过点(2.5,0),(0,25),∴解得∴y=-10x+25.
(3)联立解得∴当x=1时,甲、乙两根蜡烛在燃烧过程中的高度相等.
37.(9分)如图,在平面直角坐标系中,正方形OABC的一个顶点为B(1,1),点A,C分别在x轴,y轴上.
(1)点A的坐标为(1,0),点C的坐标为(0,1).
(2)判断直线y=-2x+与正方形OABC是否有交点,并说明理由.
(3)将直线y=-2x+进行平移,恰好能把正方形OABC分成面积相等的两部分,请求出平移后的直线的函数表达式.
【解】 (2)有交点.理由如下:把x=0代入y=-2x+,得y=;把y=0代入y=-2x+,得-2x+=0,解得x=.∴直线y=-2x+与坐标轴的交点为和.
∵OC=1,OA=1,∴直线与正方形有交点.
(3)设平移后的直线的函数表达式为y=-2x+b.由题意,易得直线y=-2x+b应经过AC与BO的交点,即过正方形OABC的中心点.把点的坐标代入y=-2x+b,得
-2×+b=,解得b=. 所求直线的函数表达式为y=-2x+.
38.(9分)某物流公司的快递车和货车每天往返于A,B两地,快递车比货车多往返一趟.下图表示快递车距离A地的路程y(km)与所用时间x(h)的函数图象.已知货车比快递车早1 h出发,到达B地后用2 h装卸货物,然后按原路、原速返回,结果比快递车最后一次返回A地晚1 h.
(1)请在图中画出货车距离A地的路程y(km)与所用时间x(h)的函数图象.
(2)求两车在途中相遇的次数(直接写出答案).
(3)求两车最后一次相遇时,距离A地的路程和货车从A地出发了几小时.
【解】 (1)如解图. (2)4次.(3)如解图,设直线EF的函数表达式为y=k1x+b1(k1≠0).
∵图象过点(9,0),(5,200),∴∴∴y=-50x+450.①
设直线CD的函数表达式为y=k2x+b2(k2≠0).∵图象过点(8,0),(6,200),
∴∴∴y=-100x+800.②联立①②,得解得∴最后一次相遇时距离A地的路程为100 km,货车从A地出发了8 h.
《6.5一次函数与二元一次方程》同步强化训练
(时间:100分钟 满分:120分)
一.选择题(每小题2分 共40分)
1.若直线y=kx+b的图象经过点(1,3),则方程kx+b=3的解是x=( )
A.1 B.2 C.3 D.4
2.已知直线y=kx+b经过点(k,3)和(1,k),则k的值为( )
A. B.± C. D.±
3.如图中的两直线l1,l2的交点坐标可以看作哪个方程组的解( )
A. B. C. D.
4.若三点(1,4),(2,7),(a,10)在同一直线上,则a的值为( )
A.-1 B.0 C.3 D.4
5.若方程组没有解,则一次函数y=1-x与y=-x的图象必定( )
A.重合 B.平行C.相交 D.无法判断
6.若以二元一次方程x+2y﹣b=0的解为坐标的点(x,y)都在直线y=﹣x+b﹣1上,则常数b=( )
A. B.2 C.﹣1 D.1
7.已知一次函数y1=2x+m与y2=2x+n(m≠n)的图象如图所示,则关于x与y的二元一次方程组的解的个数为( )
A.0个 B.1个 C.2个 D.无数个
第7题图 第8题图 第9题图 第10题图 第12题图
8.如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组的解为( )
A. B. C. D.
9.如图,过点Q(0,3)的一次函数与正比例函数y=2x的图象交于点P,能表示这个一次函数图象的方程是( )
A.3x﹣2y+3=0 B.3x﹣2y﹣3=0 C.x﹣y+3=0 D.x+y﹣3=0
10.如图中的两直线l1、l2的交点坐标可以看作哪个方程组的解( )
A. B. C. D.
11.已知和是二元一次方程ax+by+3=0的两个解,则一次函数y=ax+b(a≠0)的解析式为( )
A.y=﹣2x﹣3 B. C.y=﹣9x+3 D.
12.图中两直线l1、l2的交点坐标可以看作方程组( )的解.
A. B. C. D.
13.已知直线y=2x与y=﹣x+b的交点的坐标为(1,a),则方程组的解是( )
A. B. C. D.
14.图中两条直线l1和l2的交点坐标可以看作下列方程组( )中的解.
A. B. C. D.
第14题图 第15题图 第17题图 第18题图 第19题图
15.用图象法解二元一次方程组时,小英所画图象如图,则方程组的解为( )
A. B. C. D.
16.一次函数y=﹣2x+3的图象和y=kx﹣b的图象相交于点A(m,1),则关于x,y的二元一次方程组的解为( )
A. B. C. D.
17.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组的解是( )
A. B. C. D.
18.如图一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组的解为( )
A. B. C. D.
19.某公司准备与汽车租赁公司签订租车合同,以每月用车路程x km计算,甲汽车租赁公司每月收取的租赁费为y1元,乙汽车租赁公司每月收取的租赁费为y2元,若y1,y2与x之间的函数关系如图其中x=0对应的函数值为月固定租赁费,则下列判断错误的是( )
A.当月用车路程为2 000 km时,两家汽车租赁公司租赁费用相同
B.当月用车路程为2 300 km时,租赁乙汽车租赁公司的车比较合算
C.除去月固定租赁费,甲租赁公司每公里收取的费用比乙租赁公司多
D.甲租赁公司平均每公里收取的费用比乙租赁公司少
20.已知直线l1:y=-3x+b与直线l2:y=-kx+1在同一平面直角坐标系中的图象相交于点(1,-2),那么方程组的解是( )
A. B. C. D.
二、填空题(每小题2分 共20分)
21.直线y=kx+3与y=-x+3的图象如图3所示,则方程组的解为____.
第21题图 第22题图 第23题图 第24题图
22.一次函数y=2x-3与y=-x+1的图象的交点坐标为______.
23.如图,直线y=x+b与直线y=kx+6相交于点P(3,5),则关于x的不等式x+b>kx+6的解是__x>3__.
24.如图,观察图象,回答问题:(1)点A的横坐标是方程_____________的解.
(2)点C的横、纵坐标是方程组___________________的解.
25.无论m取何实数,直线y=x+3m与y=-x+1的交点不可能在第______象限.
26.如图,已知A,B,C,D是平面坐标系中坐标轴上的点,且△AOB≌△COD.设直线AB的函数表达式为y1=k1x+b1,直线CD的函数表达式为y2=k2x+b2,则k1·k2=___.
第26题图 第27题图 第28题图 第29题图 第30题图
27.如图,在平面直角坐标系中,四边形ABCO是正方形,点B的坐标为(4,4),直线y=mx-2恰好把正方形ABCO的面积分成相等的两部分,则m= .
28元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路程s关于行走时间t的函数图象,则两图象交点P的坐标是 .
29.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).不解关于x、y的方程组直接写出它的解___________;
30.如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是________.
三.解答题(60分)
31.(6分)如图,在平面直角坐标系xOy中,过点A(-6,0)的直线l1与直线l2:y=2x相交于点B(m,4).
(1)求直线l1的函数表达式.
(2)过动点P(n,0)且垂直于x轴的直线与l1,l2的交点分别为C,D.当点C位于点D上方时,求n的取值范围.
32.(6分)如图,在平面直角坐标系xOy中,已知正比例函数y=x与一次函数y=-x+7的图象相交于点A. (1)求点A的坐标.
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y=x和y=-x+7的图象于点B,C,连结OC.若BC=OA,求△OBC的面积.
33.(6分)学校与图书馆在同一条笔直的道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
(1)根据图象信息,当t=24时,甲、乙两人相遇,甲的速度为40米/分钟;
(2)求出线段AB所表示的函数表达式.
34.(6分)高铁的开通,给某市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题:
(1)高铁的平均速度是每小时多少千米?
(2)分别求甲、乙(乘坐高铁时)两人离N市的距离y与乘车时间x的函数关系式.
35.(9分)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2 000 kg~5 000 kg(含2 000 kg和5 000 kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货;
方案B:每千克5元,客户需支付运费2 000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(单位:元)与购买量x(单位:kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20 000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.
36.(9分)在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)的关系如图所示.请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是_____cm,_______cm,从点燃到燃尽所用的时间分别是_____h,_______h.
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数表达式.
(3)当x为何值时,甲、乙两根蜡烛在燃烧过程中的高度相等?
37.(9分)如图,在平面直角坐标系中,正方形OABC的一个顶点为B(1,1),点A,C分别在x轴,y轴上.
(1)点A的坐标为________,点C的坐标为________.
(2)判断直线y=-2x+与正方形OABC是否有交点,并说明理由.
(3)将直线y=-2x+进行平移,恰好能把正方形OABC分成面积相等的两部分,请求出平移后的直线的函数表达式.
38.(9分)某物流公司的快递车和货车每天往返于A,B两地,快递车比货车多往返一趟.下图表示快递车距离A地的路程y(km)与所用时间x(h)的函数图象.已知货车比快递车早1 h出发,到达B地后用2 h装卸货物,然后按原路、原速返回,结果比快递车最后一次返回A地晚1 h.
(1)请在图中画出货车距离A地的路程y(km)与所用时间x(h)的函数图象.
(2)求两车在途中相遇的次数(直接写出答案).
(3)求两车最后一次相遇时,距离A地的路程和货车从A地出发了几小时.
教师样卷
一.选择题(每小题2分 共40分)
1.若直线y=kx+b的图象经过点(1,3),则方程kx+b=3的解是x=( A )
A.1 B.2 C.3 D.4
2.已知直线y=kx+b经过点(k,3)和(1,k),则k的值为(B)
A. B.± C. D.±
3.如图中的两直线l1,l2的交点坐标可以看作哪个方程组的解(A)
A. B. C. D.
4.若三点(1,4),(2,7),(a,10)在同一直线上,则a的值为(C)
A.-1 B.0 C.3 D.4
5.若方程组没有解,则一次函数y=1-x与y=-x的图象必定(B)
A.重合 B.平行C.相交 D.无法判断
6.若以二元一次方程x+2y﹣b=0的解为坐标的点(x,y)都在直线y=﹣x+b﹣1上,则常数b=( B )
A. B.2 C.﹣1 D.1
7.已知一次函数y1=2x+m与y2=2x+n(m≠n)的图象如图所示,则关于x与y的二元一次方程组的解的个数为( A )
A.0个 B.1个 C.2个 D.无数个
第7题图 第8题图 第9题图 第10题图 第12题图
8.如图,两个一次函数图象的交点坐标为(2,4),则关于x,y的方程组的解为( A )
A. B. C. D.
9.如图,过点Q(0,3)的一次函数与正比例函数y=2x的图象交于点P,能表示这个一次函数图象的方程是( D )
A.3x﹣2y+3=0 B.3x﹣2y﹣3=0 C.x﹣y+3=0 D.x+y﹣3=0
10.如图中的两直线l1、l2的交点坐标可以看作哪个方程组的解( A )
A. B. C. D.
11.已知和是二元一次方程ax+by+3=0的两个解,则一次函数y=ax+b(a≠0)的解析式为( D )
A.y=﹣2x﹣3 B. C.y=﹣9x+3 D.
12.图中两直线l1、l2的交点坐标可以看作方程组( B )的解.
A. B. C. D.
13.已知直线y=2x与y=﹣x+b的交点的坐标为(1,a),则方程组的解是( A )
A. B. C. D.
14.图中两条直线l1和l2的交点坐标可以看作下列方程组( D )中的解.
A. B. C. D.
第14题图 第15题图 第17题图 第18题图 第19题图
15.用图象法解二元一次方程组时,小英所画图象如图,则方程组的解为( D )
A. B. C. D.
16.一次函数y=﹣2x+3的图象和y=kx﹣b的图象相交于点A(m,1),则关于x,y的二元一次方程组的解为( C )
A. B. C. D.
17.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组的解是( A )
A. B. C. D.
18.如图一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组的解为( A )
A. B. C. D.
19.某公司准备与汽车租赁公司签订租车合同,以每月用车路程x km计算,甲汽车租赁公司每月收取的租赁费为y1元,乙汽车租赁公司每月收取的租赁费为y2元,若y1,y2与x之间的函数关系如图其中x=0对应的函数值为月固定租赁费,则下列判断错误的是( D )
A.当月用车路程为2 000 km时,两家汽车租赁公司租赁费用相同
B.当月用车路程为2 300 km时,租赁乙汽车租赁公司的车比较合算
C.除去月固定租赁费,甲租赁公司每公里收取的费用比乙租赁公司多
D.甲租赁公司平均每公里收取的费用比乙租赁公司少
【解析】 A.交点为(2 000,2 000),那么当月用车路程为2 000 km,两家汽车租赁公司租赁费用相同,说法正确,不符合题意;B.由图象可得超过2 000 km时,相同路程,乙公司收费便宜,∴租赁乙汽车租赁公司车比较合算,说法正确,不符合题意;C.由图象易得乙的租赁费较高,当行驶2 000 km时,总收费相同,那么可得甲租赁公司每公里收取的费用比乙租赁公司多,说法正确,不符合题意;D.由图象可得平均每公里收费与路程有关,故该说法错误,符合题意,故选D.
20.已知直线l1:y=-3x+b与直线l2:y=-kx+1在同一平面直角坐标系中的图象相交于点(1,-2),那么方程组的解是(A)
A. B. C. D.
二、填空题(每小题2分 共20分)
21.直线y=kx+3与y=-x+3的图象如图3所示,则方程组的解为____.
第21题图 第22题图 第23题图 第24题图
22.一次函数y=2x-3与y=-x+1的图象的交点坐标为_(,- )_____.
23.如图,直线y=x+b与直线y=kx+6相交于点P(3,5),则关于x的不等式x+b>kx+6的解是__x>3__.
24.如图,观察图象,回答问题:(1)点A的横坐标是方程k1x+b1=0的解.
(2)点C的横、纵坐标是方程组的解.
25.无论m取何实数,直线y=x+3m与y=-x+1的交点不可能在第___三_____象限.
【解析】因为一次函数y=-x+1的图象经过一、二、四象限,所以,交点不会在第三象限.
26.如图,已知A,B,C,D是平面坐标系中坐标轴上的点,且△AOB≌△COD.设直线AB的函数表达式为y1=k1x+b1,直线CD的函数表达式为y2=k2x+b2,则k1·k2=__1__.
【解】 设点A(0,a),B(b,0),则OA=a,OB=-b.∵△AOB≌△COD,∴OC=a,OD=-b.∴点C(a,0),D(0,b).∵直线AB过点A,B,∴∴k1=-.同理可得k2=-,∴k1·k2=1.
第26题图 第27题图 第28题图 第29题图 第30题图
27.如图,在平面直角坐标系中,四边形ABCO是正方形,点B的坐标为(4,4),直线y=mx-2恰好把正方形ABCO的面积分成相等的两部分,则m= 2 .
28元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路程s关于行走时间t的函数图象,则两图象交点P的坐标是 (32,480) .
29.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).不解关于x、y的方程组直接写出它的解___________;
30.如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是________.
【答案】. 【解析】两个一次函数的交点坐标(-4,-2)即为方程组的解,即.
三.解答题(60分)
31.(6分)如图,在平面直角坐标系xOy中,过点A(-6,0)的直线l1与直线l2:y=2x相交于点B(m,4).
(1)求直线l1的函数表达式.
(2)过动点P(n,0)且垂直于x轴的直线与l1,l2的交点分别为C,D.当点C位于点D上方时,求n的取值范围.
【解】 (1)把点B(m,4)的坐标代入直线l2:y=2x,得m=2,即点B的坐标为(2,4).
设直线l2的函数表达式为y=kx+b(k≠0).由A,B两点均在直线l1上,得
解得则直线l1的函数表达式为y=x+3.
(2)由题意,得点C,D(n,2n).∵点C在点D的上方,∴+3>2n,解得n<2.
32.(6分)如图,在平面直角坐标系xOy中,已知正比例函数y=x与一次函数y=-x+7的图象相交于点A.
(1)求点A的坐标.
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y=x和y=-x+7的图象于点B,C,连结OC.若BC=OA,求△OBC的面积.
【解】 (1)联立解得∴点A(4,3).
(2)过点A作x轴的垂线,垂足为D.在Rt△OAD中,由勾股定理,得OA===5,∴BC=OA=×5=7.∵点P(a,0),∴点B,C(a,-a+7),∴BC=a-(-a+7)=a-7.∴a-7=7,解得a=8.∴S△OBC=BC·OP=×7×8=28.
33.(6分)学校与图书馆在同一条笔直的道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
(1)根据图象信息,当t=24时,甲、乙两人相遇,甲的速度为40米/分钟;
(2)求出线段AB所表示的函数表达式.
解:因为t=24时甲、乙两人相遇,所以甲、乙两人的速度和为2 400÷24=100(米/分钟).
所以乙的速度为100-40=60(米/分钟).
乙从图书馆回学校的时间为2 400÷60=40(分钟).
100×(40-24)=1 600,
所以A点的坐标为(40,1 600).
设线段AB所表示的函数表达式为y=kt+b,
因为A(40,1 600),B(60,2 400),
所以解得
所以线段AB所表示的函数表达式为y=40t(40≤t≤60).
34.(6分)高铁的开通,给某市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题:
(1)高铁的平均速度是每小时多少千米?
(2)分别求甲、乙(乘坐高铁时)两人离N市的距离y与乘车时间x的函数关系式.
解:(1)420÷(2.5-1)=280(千米/小时).
答:高铁的平均速度是每小时280千米.
(2)设甲离N市的距离y与乘车时间x的函数关系式为y甲=kx(k≠0),乙(乘坐高铁时)离N市的距离y与乘车时间x的函数关系式为y乙=mx+n(m≠0).
将点(1,0),(2.5,420)代入y乙=mx+n,得
解得
所以乙(乘坐高铁时)离N市的距离y与乘车时间x的函数关系式为y乙=280x-280(1≤x≤2.5).
当y乙=112时,280x-280=112,解得x=1.4.
将(1.4,112)代入y甲=kx,得
1.4k=112,解得k=80,
所以甲离N市的距离y与乘车时间x的函数关系式为y甲=80x.
35.(9分)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2 000 kg~5 000 kg(含2 000 kg和5 000 kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货;
方案B:每千克5元,客户需支付运费2 000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(单位:元)与购买量x(单位:kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20 000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.
解:(1)方案A:函数表达式为y=5.8x.方案B:函数表达式为y=5x+2 000;
(2)由题意,得5.8x<5x+2 000,解得x<2 500, ∴当购买量x的取值范围为2 000≤x<2 500时,选用方案A比方案B付款少;
(3)他应选择方案B.
36.(9分)在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)的关系如图所示.请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是30_cm,25_cm,从点燃到燃尽所用的时间分别是2_h,2.5_h.
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数表达式.
(3)当x为何值时,甲、乙两根蜡烛在燃烧过程中的高度相等?
【解】 (2)设甲蜡烛燃烧时y与x之间的函数表达式为y=k1x+b1.由图可知,函数的图象过点(2,0),(0,30),∴解得∴y=-15x+30.
设乙蜡烛燃烧时y与x之间的函数表达式为y=k2x+b2.由图可知,函数的图象过点(2.5,0),(0,25),∴解得∴y=-10x+25.
(3)联立解得∴当x=1时,甲、乙两根蜡烛在燃烧过程中的高度相等.
37.(9分)如图,在平面直角坐标系中,正方形OABC的一个顶点为B(1,1),点A,C分别在x轴,y轴上.
(1)点A的坐标为(1,0),点C的坐标为(0,1).
(2)判断直线y=-2x+与正方形OABC是否有交点,并说明理由.
(3)将直线y=-2x+进行平移,恰好能把正方形OABC分成面积相等的两部分,请求出平移后的直线的函数表达式.
【解】 (2)有交点.理由如下:把x=0代入y=-2x+,得y=;把y=0代入y=-2x+,得-2x+=0,解得x=.∴直线y=-2x+与坐标轴的交点为和.
∵OC=1,OA=1,∴直线与正方形有交点.
(3)设平移后的直线的函数表达式为y=-2x+b.由题意,易得直线y=-2x+b应经过AC与BO的交点,即过正方形OABC的中心点.把点的坐标代入y=-2x+b,得
-2×+b=,解得b=. 所求直线的函数表达式为y=-2x+.
38.(9分)某物流公司的快递车和货车每天往返于A,B两地,快递车比货车多往返一趟.下图表示快递车距离A地的路程y(km)与所用时间x(h)的函数图象.已知货车比快递车早1 h出发,到达B地后用2 h装卸货物,然后按原路、原速返回,结果比快递车最后一次返回A地晚1 h.
(1)请在图中画出货车距离A地的路程y(km)与所用时间x(h)的函数图象.
(2)求两车在途中相遇的次数(直接写出答案).
(3)求两车最后一次相遇时,距离A地的路程和货车从A地出发了几小时.
【解】 (1)如解图. (2)4次.(3)如解图,设直线EF的函数表达式为y=k1x+b1(k1≠0).
∵图象过点(9,0),(5,200),∴∴∴y=-50x+450.①
设直线CD的函数表达式为y=k2x+b2(k2≠0).∵图象过点(8,0),(6,200),
∴∴∴y=-100x+800.②联立①②,得解得∴最后一次相遇时距离A地的路程为100 km,货车从A地出发了8 h.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
