2021-2022学年人教版数学九年级上册24.1.2垂直于弦的直径同步习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.1.2垂直于弦的直径同步习题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 397.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 16:28:10 | ||
图片预览



文档简介
2021-2022学年初中数学九年级上册(人教版)
24.1.2垂直于弦的直径-同步习题
时间:40分钟
一、单选题
1.已知:如图,是的直径,弦交于E点,,则的长为( )
A. B. C. D.4
2.如图,半圆的直径,为圆心,为的中点,,交于点,则弦的长为( )
A. B. C. D.
3.下列说法中正确的有( )
①垂直平分弦的直线经过圆心;
②平分弦的直径一定垂直于弦;
③一条直线平分弦,那么这条直线垂直这条弦;
④平分弦的直线,必定过圆心;
⑤平分弦的直径,平分这条弦所对的弧.
A.1个 B.2个 C.3个 D.4个
4.下列说法中错误的有( )
①过弦的中点的直线平分弦所对的两条弧;
②弦的垂线平分它所对的两条弧;
③过弦的中点的直径平分弦所对的两条弧;
④平分不是直径的弦的直径平分弦所对的两条弧.
A.1个 B.2个 C.3个 D.4个
5.过⊙O内一点M的最长弦为10cm,最短弦长为8cm,则OM的长为( )
A.9cm B.6cm C.3cm D.cm
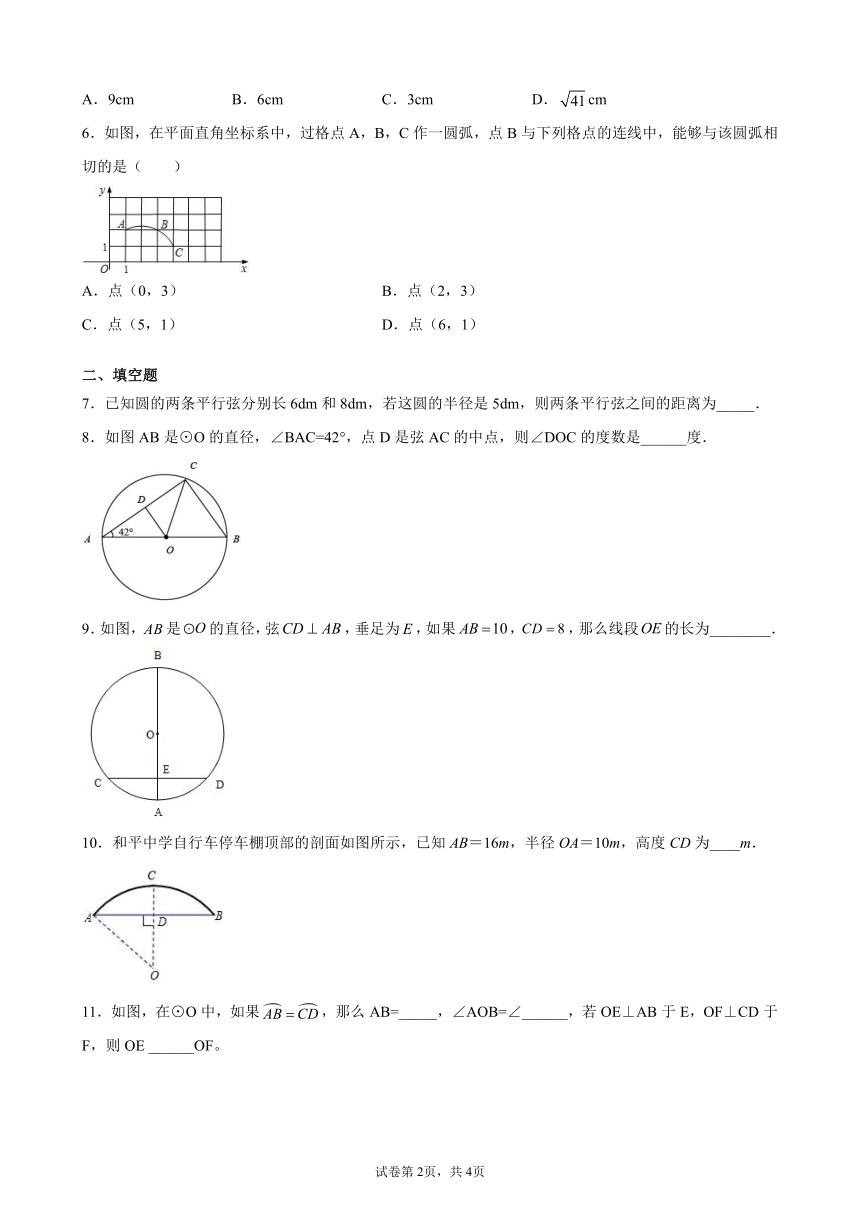
6.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A.点(0,3) B.点(2,3)
C.点(5,1) D.点(6,1)
二、填空题
7.已知圆的两条平行弦分别长6dm和8dm,若这圆的半径是5dm,则两条平行弦之间的距离为_____.
8.如图AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是______度.
9.如图,是的直径,弦,垂足为,如果,,那么线段的长为________.
10.和平中学自行车停车棚顶部的剖面如图所示,已知AB=16m,半径OA=10m,高度CD为____m.
11.如图,在⊙O中,如果,那么AB=_____,∠AOB=∠______,若OE⊥AB于E,OF⊥CD于F,则OE ______OF。
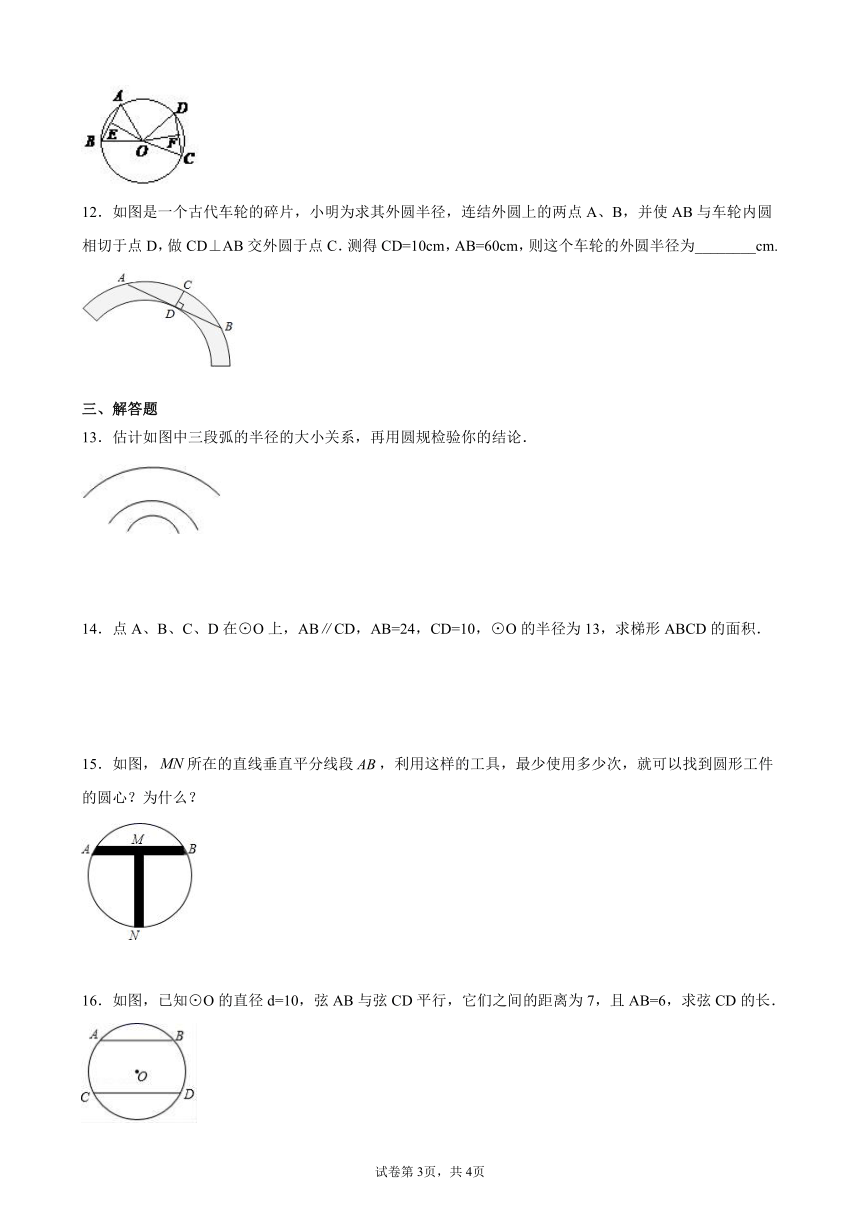
12.如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,做CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径为________cm.
三、解答题
13.估计如图中三段弧的半径的大小关系,再用圆规检验你的结论.
14.点A、B、C、D在⊙O上,AB∥CD,AB=24,CD=10,⊙O的半径为13,求梯形ABCD的面积.
15.如图,所在的直线垂直平分线段,利用这样的工具,最少使用多少次,就可以找到圆形工件的圆心?为什么?
16.如图,已知⊙O的直径d=10,弦AB与弦CD平行,它们之间的距离为7,且AB=6,求弦CD的长.
17.如图,,是的两条弦,,垂足为点,,,,,求的半径.
18.往直径为的圆柱形油槽内装入一些油以后,截面如图所示.若油面宽,求油的最大深度.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
【解析】如图,过点作于,
则,
,
,
,
,
,
,
,
.
故选A.
2.A
【解析】解:如图所示,连接,
∵,,
∴,
∴,即.
∵,
∴,
∵为的中点,
∴,
在中,,,
∴,
∴.
故选A.
3.A
【解析】解:①根据垂径定理的推论可知,垂直平分弦的直线经过圆心,故①正确;
②任意两条直径互相平分,但不一定互相垂直,故被平分弦不能是直径,故②错误,同理⑤也错误;
③只要过弦的中点的直线就会平分弦,但未必和弦垂直,故③错误;
④同③可知平分弦的直线不一定会过圆心,故④错误;
∴正确的有1个,
故选:A.
4.C
【解析】①中若直线与弦不垂直,则结论不成立;
②若垂线不是直径,则结论不成立;
③若所过的弦中点故选:C所在的弦本身就是直径,则结论不成立.
故①②③都不正确,④正确.
故选:C
5.C
【解析】解:由题意知,最长的弦为直径,最短的弦为垂直于直径的弦,
如图所示.直径ED⊥AB于点M,
则ED=10cm,AB=8cm,
由垂径定理知:点M为AB中点,
∴AM=4cm,
∵半径OA=5cm,
∴OM2=OA2-AM2=25-16=9,
∴OM=3cm.
故选:C.
6.C
【解析】∵过格点A,B,C作一圆弧,∴三点组成的圆的圆心为:O(2,0),∵只有∠OBD+∠EBF=90°时,BF与圆相切,∴当△BOD≌△FBE时,∴EF=BD=2,F点的坐标为:(5,1),∴点B与下列格点的连线中,能够与该圆弧相切的是:(5,1).故选C.
7.7dm或1dm
【解析】解:如图,AB∥CD,AB=6dm,CD=8dm,
过O点作OE⊥AB于E,交CD于F点,连OA、OC,
∴AE=BE=AB=3,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴CF=FD=CD=4,
在Rt△OAE中,OA=5dm
OE==4,
同理可得OF=3,
当圆心O在AB与CD之间时,AB与CD的距离=OE+OF=4+3=7(dm);
当圆心O不在AB与CD之间时,AB与CD的距离=OE﹣OF=4﹣3=1(dm).
故答案为7dm或1dm.
8.48
【解析】∵AB是⊙O的直径,∴OA=OC.
∵∠A=42°,∴∠ACO=∠A=42°.
∵D为AC的中点,∴OD⊥AC.
∴∠DOC=90°﹣∠DCO=90°﹣42°=48°.
9.3
【解析】连接,
在中,
,,
由勾股定理,得,
即线段的长为3.
故答案为:
10.4.
【解析】解:∵CD⊥AB,AB=16,
∴AD=DB=8,
在Rt△OAD中,AB=16m,半径OA=10m,
∴OD==6,
∴CD=OC﹣OD=10﹣6=4(m).
故答案为4.
11.CD COD =
【解析】∵=,
∴AB=CD,∠AOB=∠DOC,
∵AO=DO,BO=CO,∠AOB=∠DOC,
∴△AOB≌△DOC,
∵OE、OF均为对应边上的高,
∴OE=OF.
12.50
【解析】如图,设点O为外圆的圆心,连接OA和OC,
∵CD=10cm,AB=60cm,
∵CD⊥AB,
∴OC⊥AB,
∴
∴设半径为r,则OD=r 10,
根据题意得:
解得:r=50.
∴这个车轮的外圆半径长为50.
故答案为50.
13.见解析
【解析】解:①在较大的弧上取点A、B,连接AB,使线段AB同时过三条弧,再作AB的垂直平分线CD;
②连接DE,作DE的垂直平分线交CD与点O″,则此点即为 所在圆的圆心;
③连接GF,作GF的垂直平分线交CD与点O′,则O′即为中间的弧所在圆的圆心;
④连接BC,作BC的垂直平分线交CD与点O,则O即为较大的弧所在圆的圆心.
根据图形可知:最上面的弧的半径最大,最下面的弧的半径最小.
14.289或119
【解析】
解:连接OA、OD,作OE⊥AB,OF⊥CD,垂足分别为E、F,在Rt△AOE中,OA=13,AE=12,OE==5;同理可得OF=12
分两种情况:如图1.EF=OF+OE=12+5=17
如图2.EF=OF-OE=12-5=7
因此梯形的面积为(AB+CD)EF=(24+10)EF=289或119.
故答案为:289或119.
15.最少用2次,见解析
【解析】解:如图所示,根据垂径定理的推论,两个直径的交点即为圆心.
故最少使用2次就可以找到圆形工件的圆心.
16.8
【解析】作OM⊥AB于M,ON⊥CD于N,连接OA、OC,
则
∵AB∥CD,
∴点M、O、N在同一条直线上,
在Rt△AOM中,
∴ON=MN﹣OM=3,
在Rt△CON中,
∵ON⊥CD,
∴CD=2CN=8.
17.的半径为
【解析】解:如图,作于,于,连接,
则,,
∵,,,,
∴,,
∴,,
∴,
∵,,,
∴四边形是矩形,
∴,
在中,,即的半径为.
18.200mm
【解析】解:过点O作OD⊥AB于点D,交于点F,连接OA,
∵AB=600mm,
∴AD==300mm,
∵直径为650mm,
∴OA=×650=325mm,
∴OD===125mm,
∴DF=OF OD=×650 125=200mm.
答:油的最大深度为200mm.
答案第1页,共2页
答案第1页,共2页
24.1.2垂直于弦的直径-同步习题
时间:40分钟
一、单选题
1.已知:如图,是的直径,弦交于E点,,则的长为( )
A. B. C. D.4
2.如图,半圆的直径,为圆心,为的中点,,交于点,则弦的长为( )
A. B. C. D.
3.下列说法中正确的有( )
①垂直平分弦的直线经过圆心;
②平分弦的直径一定垂直于弦;
③一条直线平分弦,那么这条直线垂直这条弦;
④平分弦的直线,必定过圆心;
⑤平分弦的直径,平分这条弦所对的弧.
A.1个 B.2个 C.3个 D.4个
4.下列说法中错误的有( )
①过弦的中点的直线平分弦所对的两条弧;
②弦的垂线平分它所对的两条弧;
③过弦的中点的直径平分弦所对的两条弧;
④平分不是直径的弦的直径平分弦所对的两条弧.
A.1个 B.2个 C.3个 D.4个
5.过⊙O内一点M的最长弦为10cm,最短弦长为8cm,则OM的长为( )
A.9cm B.6cm C.3cm D.cm
6.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A.点(0,3) B.点(2,3)
C.点(5,1) D.点(6,1)
二、填空题
7.已知圆的两条平行弦分别长6dm和8dm,若这圆的半径是5dm,则两条平行弦之间的距离为_____.
8.如图AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是______度.
9.如图,是的直径,弦,垂足为,如果,,那么线段的长为________.
10.和平中学自行车停车棚顶部的剖面如图所示,已知AB=16m,半径OA=10m,高度CD为____m.
11.如图,在⊙O中,如果,那么AB=_____,∠AOB=∠______,若OE⊥AB于E,OF⊥CD于F,则OE ______OF。
12.如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,做CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径为________cm.
三、解答题
13.估计如图中三段弧的半径的大小关系,再用圆规检验你的结论.
14.点A、B、C、D在⊙O上,AB∥CD,AB=24,CD=10,⊙O的半径为13,求梯形ABCD的面积.
15.如图,所在的直线垂直平分线段,利用这样的工具,最少使用多少次,就可以找到圆形工件的圆心?为什么?
16.如图,已知⊙O的直径d=10,弦AB与弦CD平行,它们之间的距离为7,且AB=6,求弦CD的长.
17.如图,,是的两条弦,,垂足为点,,,,,求的半径.
18.往直径为的圆柱形油槽内装入一些油以后,截面如图所示.若油面宽,求油的最大深度.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
【解析】如图,过点作于,
则,
,
,
,
,
,
,
,
.
故选A.
2.A
【解析】解:如图所示,连接,
∵,,
∴,
∴,即.
∵,
∴,
∵为的中点,
∴,
在中,,,
∴,
∴.
故选A.
3.A
【解析】解:①根据垂径定理的推论可知,垂直平分弦的直线经过圆心,故①正确;
②任意两条直径互相平分,但不一定互相垂直,故被平分弦不能是直径,故②错误,同理⑤也错误;
③只要过弦的中点的直线就会平分弦,但未必和弦垂直,故③错误;
④同③可知平分弦的直线不一定会过圆心,故④错误;
∴正确的有1个,
故选:A.
4.C
【解析】①中若直线与弦不垂直,则结论不成立;
②若垂线不是直径,则结论不成立;
③若所过的弦中点故选:C所在的弦本身就是直径,则结论不成立.
故①②③都不正确,④正确.
故选:C
5.C
【解析】解:由题意知,最长的弦为直径,最短的弦为垂直于直径的弦,
如图所示.直径ED⊥AB于点M,
则ED=10cm,AB=8cm,
由垂径定理知:点M为AB中点,
∴AM=4cm,
∵半径OA=5cm,
∴OM2=OA2-AM2=25-16=9,
∴OM=3cm.
故选:C.
6.C
【解析】∵过格点A,B,C作一圆弧,∴三点组成的圆的圆心为:O(2,0),∵只有∠OBD+∠EBF=90°时,BF与圆相切,∴当△BOD≌△FBE时,∴EF=BD=2,F点的坐标为:(5,1),∴点B与下列格点的连线中,能够与该圆弧相切的是:(5,1).故选C.
7.7dm或1dm
【解析】解:如图,AB∥CD,AB=6dm,CD=8dm,
过O点作OE⊥AB于E,交CD于F点,连OA、OC,
∴AE=BE=AB=3,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴CF=FD=CD=4,
在Rt△OAE中,OA=5dm
OE==4,
同理可得OF=3,
当圆心O在AB与CD之间时,AB与CD的距离=OE+OF=4+3=7(dm);
当圆心O不在AB与CD之间时,AB与CD的距离=OE﹣OF=4﹣3=1(dm).
故答案为7dm或1dm.
8.48
【解析】∵AB是⊙O的直径,∴OA=OC.
∵∠A=42°,∴∠ACO=∠A=42°.
∵D为AC的中点,∴OD⊥AC.
∴∠DOC=90°﹣∠DCO=90°﹣42°=48°.
9.3
【解析】连接,
在中,
,,
由勾股定理,得,
即线段的长为3.
故答案为:
10.4.
【解析】解:∵CD⊥AB,AB=16,
∴AD=DB=8,
在Rt△OAD中,AB=16m,半径OA=10m,
∴OD==6,
∴CD=OC﹣OD=10﹣6=4(m).
故答案为4.
11.CD COD =
【解析】∵=,
∴AB=CD,∠AOB=∠DOC,
∵AO=DO,BO=CO,∠AOB=∠DOC,
∴△AOB≌△DOC,
∵OE、OF均为对应边上的高,
∴OE=OF.
12.50
【解析】如图,设点O为外圆的圆心,连接OA和OC,
∵CD=10cm,AB=60cm,
∵CD⊥AB,
∴OC⊥AB,
∴
∴设半径为r,则OD=r 10,
根据题意得:
解得:r=50.
∴这个车轮的外圆半径长为50.
故答案为50.
13.见解析
【解析】解:①在较大的弧上取点A、B,连接AB,使线段AB同时过三条弧,再作AB的垂直平分线CD;
②连接DE,作DE的垂直平分线交CD与点O″,则此点即为 所在圆的圆心;
③连接GF,作GF的垂直平分线交CD与点O′,则O′即为中间的弧所在圆的圆心;
④连接BC,作BC的垂直平分线交CD与点O,则O即为较大的弧所在圆的圆心.
根据图形可知:最上面的弧的半径最大,最下面的弧的半径最小.
14.289或119
【解析】
解:连接OA、OD,作OE⊥AB,OF⊥CD,垂足分别为E、F,在Rt△AOE中,OA=13,AE=12,OE==5;同理可得OF=12
分两种情况:如图1.EF=OF+OE=12+5=17
如图2.EF=OF-OE=12-5=7
因此梯形的面积为(AB+CD)EF=(24+10)EF=289或119.
故答案为:289或119.
15.最少用2次,见解析
【解析】解:如图所示,根据垂径定理的推论,两个直径的交点即为圆心.
故最少使用2次就可以找到圆形工件的圆心.
16.8
【解析】作OM⊥AB于M,ON⊥CD于N,连接OA、OC,
则
∵AB∥CD,
∴点M、O、N在同一条直线上,
在Rt△AOM中,
∴ON=MN﹣OM=3,
在Rt△CON中,
∵ON⊥CD,
∴CD=2CN=8.
17.的半径为
【解析】解:如图,作于,于,连接,
则,,
∵,,,,
∴,,
∴,,
∴,
∵,,,
∴四边形是矩形,
∴,
在中,,即的半径为.
18.200mm
【解析】解:过点O作OD⊥AB于点D,交于点F,连接OA,
∵AB=600mm,
∴AD==300mm,
∵直径为650mm,
∴OA=×650=325mm,
∴OD===125mm,
∴DF=OF OD=×650 125=200mm.
答:油的最大深度为200mm.
答案第1页,共2页
答案第1页,共2页
同课章节目录
