2021—2022学年人教版九年级数学上册24.2.2 直线与圆的位置关系(第三课时)课后练习(word版含简单答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学上册24.2.2 直线与圆的位置关系(第三课时)课后练习(word版含简单答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 201.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 18:32:32 | ||
图片预览


文档简介
2021——2022学年度人教版九年级数学上册 第二十四章 圆
24.2.2 直线与圆的位置关系(第三课时)课后练习
一、选择题
1.若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为( )
A. B. C. D.
2.如图,PA与⊙O相切于点A,线段PO交⊙O于点C,过点C作⊙O的切线交PA于点B.若PC=4,AB=3,则⊙O的半径等于( )
A.4 B.5 C.6 D.12
3.如图,PA,PB为⊙O的两条切线,点A,B是切点,OP交⊙O于点C,交弦AB于点D.下列结论中错误的是( )
A.PA=PB B.AD=BD C.OP⊥AB D.∠PAB=∠APB
4.如图,PA,PB为⊙O的切线,A,B为切点,根据图形得出四个结论:①PA=PB;②∠1=∠2;③∠3=∠4;④AB被OP垂直平分. 其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
5.如图,切于点切于点交于点,下列结论中不一定成立的是( )
A. B.平分
C. D.
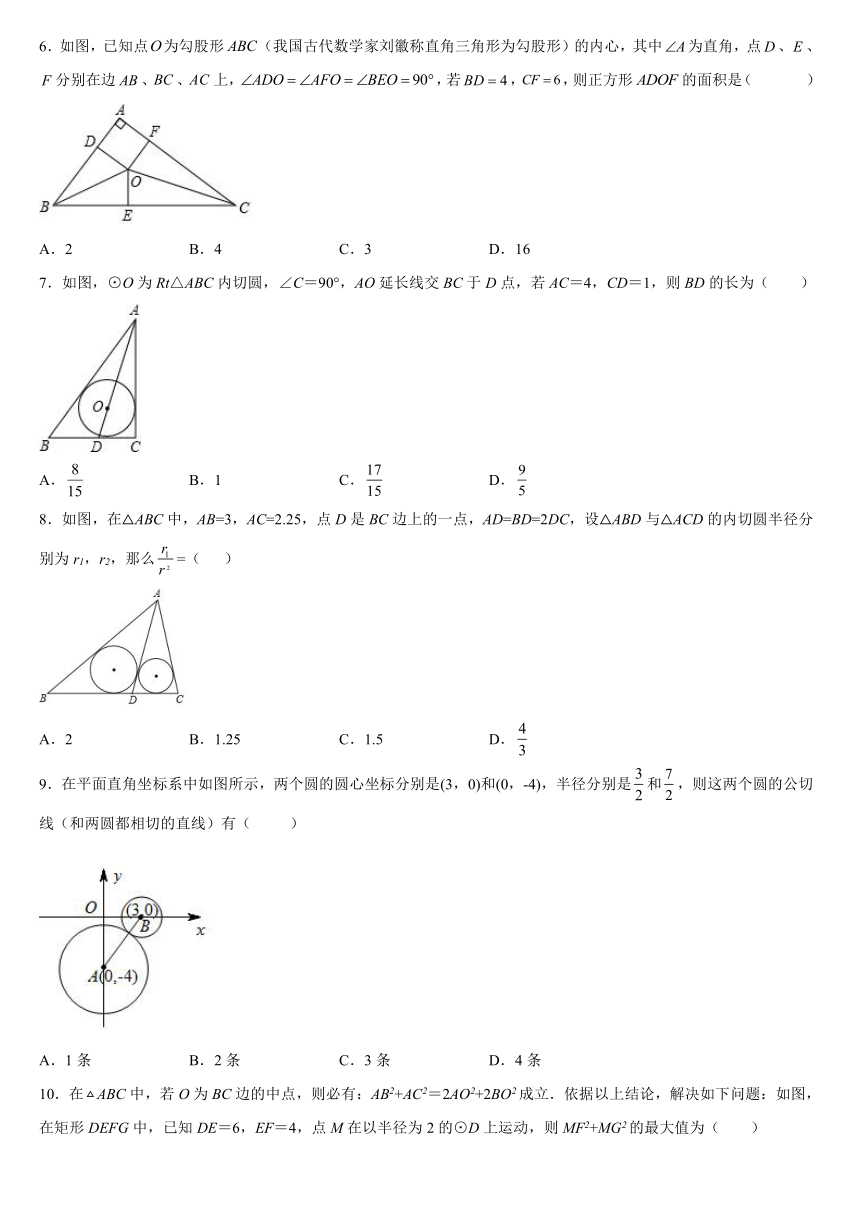
6.如图,已知点为勾股形(我国古代数学家刘徽称直角三角形为勾股形)的内心,其中为直角,点、、分别在边、、上,,若,,则正方形的面积是( )
A.2 B.4 C.3 D.16
7.如图,⊙O为Rt△ABC内切圆,∠C=90°,AO延长线交BC于D点,若AC=4,CD=1,则BD的长为( )
A. B.1 C. D.
8.如图,在△ABC中,AB=3,AC=2.25,点D是BC边上的一点,AD=BD=2DC,设△ABD与△ACD的内切圆半径分别为r1,r2,那么=( )
A.2 B.1.25 C.1.5 D.
9.在平面直角坐标系中如图所示,两个圆的圆心坐标分别是(3,0)和(0,-4),半径分别是和,则这两个圆的公切线(和两圆都相切的直线)有( )
A.1条 B.2条 C.3条 D.4条
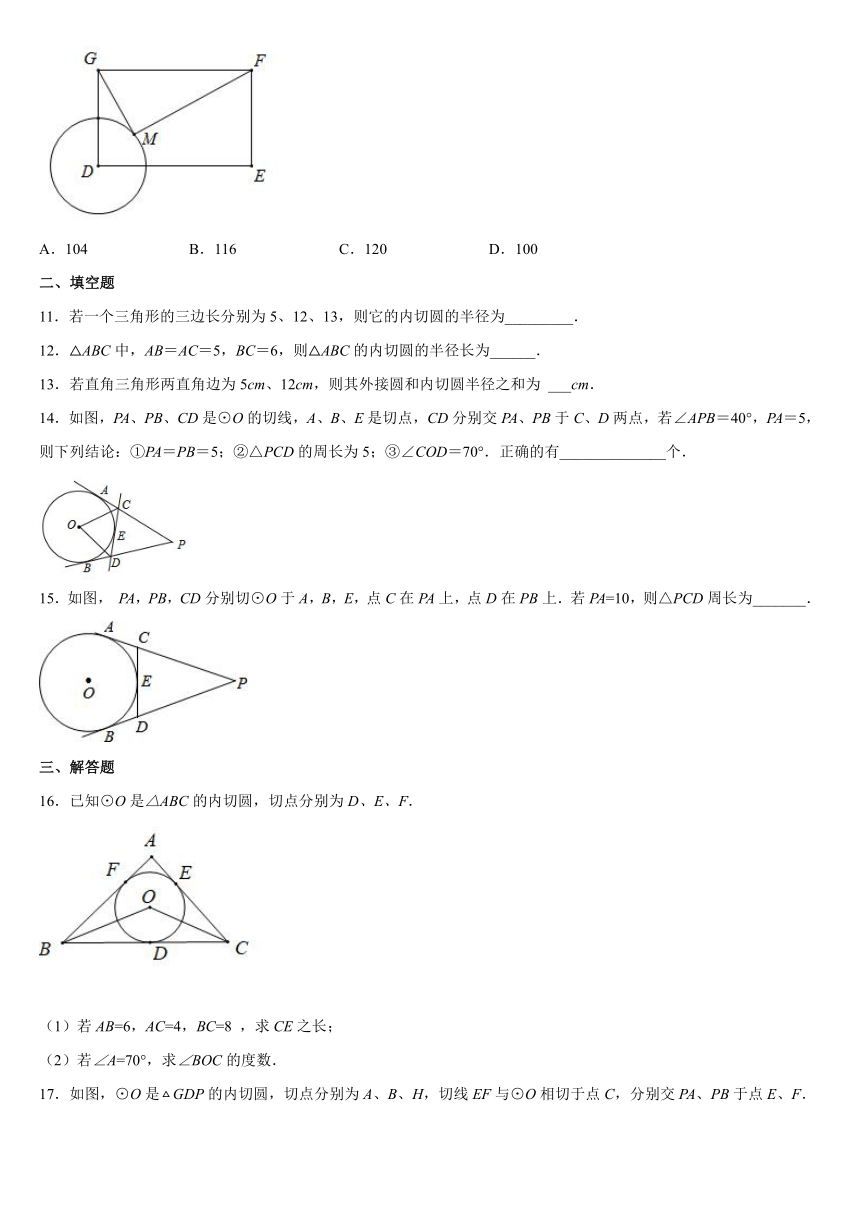
10.在ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=6,EF=4,点M在以半径为2的⊙D上运动,则MF2+MG2的最大值为( )
A.104 B.116 C.120 D.100
二、填空题
11.若一个三角形的三边长分别为5、12、13,则它的内切圆的半径为_________.
12.△ABC中,AB=AC=5,BC=6,则△ABC的内切圆的半径长为______.
13.若直角三角形两直角边为5cm、12cm,则其外接圆和内切圆半径之和为 ___cm.
14.如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点,若∠APB=40°,PA=5,则下列结论:①PA=PB=5;②△PCD的周长为5;③∠COD=70°.正确的有______________个.
15.如图, PA,PB,CD分别切⊙O于A,B,E,点C在PA上,点D在PB上.若PA=10,则△PCD周长为_______.
三、解答题
16.已知⊙O是△ABC的内切圆,切点分别为D、E、F.
(1)若AB=6,AC=4,BC=8 ,求CE之长;
(2)若∠A=70°,求∠BOC的度数.
17.如图,⊙O是GDP的内切圆,切点分别为A、B、H,切线EF与⊙O相切于点C,分别交PA、PB于点E、F.
(1)若△PEF的周长为12,求线段PA的长;
(2)若∠G=90°,GD=3,GP=4,求⊙O半径.
18.如图,AB,BC,CD分别与⊙O相切于E,F,G三点,且AB//CD,BO=6cm,CO=8cm.求BC的长及⊙O的半径.
19.阅读材料:
已知a,b为两个正实数,∵a+b﹣2()2+()2﹣2 ()2≥0,∴a+b≥2,即:,当且仅当“a=b”时,等号成立.我们把叫做正数a,b的算术平均数,把叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最值问题的有力工具.示例:当x>0时,求y=x1的最小值;
解:y=(x)+121=3,当x,即x=1时,y的最小值为3.
(1)探究:当x>0时,求y的最小值;
(2)知识迁移:随着人们生活水平的提高,汽车已成为越来越多家庭的交通工具,假设某种汽车的购车费用为10万元,每年应缴保险费等各类费用共计0.4万元,n年的保养,维修费用总和为万元,问这种汽车使用多少年报废最合算(即使用多少年的年平均费用最少,年平均费用=所有费用:年数n)?最少年平均费用为多少万元?
(3)创新应用:如图,在直角坐标系中,直线AB经点P(3,4),与坐标轴正半轴相交于A,B两点,当△AOB的面积最小时,求△AOB的内切圆的半径.
20.如图,一块等腰三角形钢板的底边长为,腰长为.
(1)求能从这块钢板上截得的最大圆的半径;
(2)用一个圆完整覆盖这块钢板,这个圆的最小半径是多少?
21.如图,⊙A、⊙B、⊙C两两外切,AB=10,BC=21,sinB=.
(1)求AC的长;
(2)求⊙A、⊙B、⊙C半径.
22.在一次数学探究活动中,王老师设计了一份活动单:已知线段BC=2,使用作图工具作∠BAC=30°,尝试操作后思考:
(1)这样的点A唯一吗?
(2)点A的位置有什么特征?你有什么感悟?
“追梦”学习小组通过操作、观察、讨论后汇报:点A的位置不唯一,它在以BC为弦的圆弧上(点B、C除外),….小华同学画出了符合要求的一条圆弧(如图1).
(1)小华同学提出了下列问题,请你帮助解决.①该弧所在圆的半径长为 ;②△ABC面积的最大值为 ;
(2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为A′,请你利用图1证明∠BA′C>30°.
(3)请你运用所学知识,结合以上活动经验,解决问题:如图2,在平面直角坐标系的第一象限内有一点B,坐标为(2,m),过点B作AB⊥y轴,BC⊥x轴,垂足分别为A、C,若点P在线段AB上滑动(点P可以与点A、B重合),发现使得∠OPC=45°的位置有两个,则m的取值范围为 .
23.阅读材料:如图(一),△ABC的周长为l,内切圆O的半径为r,连接OA,OB,OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积.
∵S△ABC=S△OAB+S△OBC+S△OCA
又∵S△OABAB r,S△OBCBC r,S△OCACA r
∴S△ABCAB rBC rCA rl r
∴r(可作为三角形内切圆半径公式)
根据上述阅读材料完成下列各题:
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、a3、…、an,合理猜想其内切圆半径公式(不需说明理由).
【参考答案】
1.B 2.C 3.D 4.D 5.D 6.B 7.C 8.C 9.C 10.B
11.2
12.
13.8.5
14.2
15.20
16.(1);(2)
17.(1)6;(2)1
18.BC=10cm,半径为cm.
19.(1)最小值为5;(2)这种汽车使用10年报废最合算,最少年平均费用为2.5万元;(3)r=2.
20.(1)cm;(2)40cm.
21.(1)17;(2)rA=3,rB=7,rC=14
22.(1)①2;②+2;(2)略;(3).
23.(1)边长分为5、12、13的三角形内切圆半径为2;(2)r;(3)内切圆半径r
24.2.2 直线与圆的位置关系(第三课时)课后练习
一、选择题
1.若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为( )
A. B. C. D.
2.如图,PA与⊙O相切于点A,线段PO交⊙O于点C,过点C作⊙O的切线交PA于点B.若PC=4,AB=3,则⊙O的半径等于( )
A.4 B.5 C.6 D.12
3.如图,PA,PB为⊙O的两条切线,点A,B是切点,OP交⊙O于点C,交弦AB于点D.下列结论中错误的是( )
A.PA=PB B.AD=BD C.OP⊥AB D.∠PAB=∠APB
4.如图,PA,PB为⊙O的切线,A,B为切点,根据图形得出四个结论:①PA=PB;②∠1=∠2;③∠3=∠4;④AB被OP垂直平分. 其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
5.如图,切于点切于点交于点,下列结论中不一定成立的是( )
A. B.平分
C. D.
6.如图,已知点为勾股形(我国古代数学家刘徽称直角三角形为勾股形)的内心,其中为直角,点、、分别在边、、上,,若,,则正方形的面积是( )
A.2 B.4 C.3 D.16
7.如图,⊙O为Rt△ABC内切圆,∠C=90°,AO延长线交BC于D点,若AC=4,CD=1,则BD的长为( )
A. B.1 C. D.
8.如图,在△ABC中,AB=3,AC=2.25,点D是BC边上的一点,AD=BD=2DC,设△ABD与△ACD的内切圆半径分别为r1,r2,那么=( )
A.2 B.1.25 C.1.5 D.
9.在平面直角坐标系中如图所示,两个圆的圆心坐标分别是(3,0)和(0,-4),半径分别是和,则这两个圆的公切线(和两圆都相切的直线)有( )
A.1条 B.2条 C.3条 D.4条
10.在ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=6,EF=4,点M在以半径为2的⊙D上运动,则MF2+MG2的最大值为( )
A.104 B.116 C.120 D.100
二、填空题
11.若一个三角形的三边长分别为5、12、13,则它的内切圆的半径为_________.
12.△ABC中,AB=AC=5,BC=6,则△ABC的内切圆的半径长为______.
13.若直角三角形两直角边为5cm、12cm,则其外接圆和内切圆半径之和为 ___cm.
14.如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点,若∠APB=40°,PA=5,则下列结论:①PA=PB=5;②△PCD的周长为5;③∠COD=70°.正确的有______________个.
15.如图, PA,PB,CD分别切⊙O于A,B,E,点C在PA上,点D在PB上.若PA=10,则△PCD周长为_______.
三、解答题
16.已知⊙O是△ABC的内切圆,切点分别为D、E、F.
(1)若AB=6,AC=4,BC=8 ,求CE之长;
(2)若∠A=70°,求∠BOC的度数.
17.如图,⊙O是GDP的内切圆,切点分别为A、B、H,切线EF与⊙O相切于点C,分别交PA、PB于点E、F.
(1)若△PEF的周长为12,求线段PA的长;
(2)若∠G=90°,GD=3,GP=4,求⊙O半径.
18.如图,AB,BC,CD分别与⊙O相切于E,F,G三点,且AB//CD,BO=6cm,CO=8cm.求BC的长及⊙O的半径.
19.阅读材料:
已知a,b为两个正实数,∵a+b﹣2()2+()2﹣2 ()2≥0,∴a+b≥2,即:,当且仅当“a=b”时,等号成立.我们把叫做正数a,b的算术平均数,把叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最值问题的有力工具.示例:当x>0时,求y=x1的最小值;
解:y=(x)+121=3,当x,即x=1时,y的最小值为3.
(1)探究:当x>0时,求y的最小值;
(2)知识迁移:随着人们生活水平的提高,汽车已成为越来越多家庭的交通工具,假设某种汽车的购车费用为10万元,每年应缴保险费等各类费用共计0.4万元,n年的保养,维修费用总和为万元,问这种汽车使用多少年报废最合算(即使用多少年的年平均费用最少,年平均费用=所有费用:年数n)?最少年平均费用为多少万元?
(3)创新应用:如图,在直角坐标系中,直线AB经点P(3,4),与坐标轴正半轴相交于A,B两点,当△AOB的面积最小时,求△AOB的内切圆的半径.
20.如图,一块等腰三角形钢板的底边长为,腰长为.
(1)求能从这块钢板上截得的最大圆的半径;
(2)用一个圆完整覆盖这块钢板,这个圆的最小半径是多少?
21.如图,⊙A、⊙B、⊙C两两外切,AB=10,BC=21,sinB=.
(1)求AC的长;
(2)求⊙A、⊙B、⊙C半径.
22.在一次数学探究活动中,王老师设计了一份活动单:已知线段BC=2,使用作图工具作∠BAC=30°,尝试操作后思考:
(1)这样的点A唯一吗?
(2)点A的位置有什么特征?你有什么感悟?
“追梦”学习小组通过操作、观察、讨论后汇报:点A的位置不唯一,它在以BC为弦的圆弧上(点B、C除外),….小华同学画出了符合要求的一条圆弧(如图1).
(1)小华同学提出了下列问题,请你帮助解决.①该弧所在圆的半径长为 ;②△ABC面积的最大值为 ;
(2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为A′,请你利用图1证明∠BA′C>30°.
(3)请你运用所学知识,结合以上活动经验,解决问题:如图2,在平面直角坐标系的第一象限内有一点B,坐标为(2,m),过点B作AB⊥y轴,BC⊥x轴,垂足分别为A、C,若点P在线段AB上滑动(点P可以与点A、B重合),发现使得∠OPC=45°的位置有两个,则m的取值范围为 .
23.阅读材料:如图(一),△ABC的周长为l,内切圆O的半径为r,连接OA,OB,OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积.
∵S△ABC=S△OAB+S△OBC+S△OCA
又∵S△OABAB r,S△OBCBC r,S△OCACA r
∴S△ABCAB rBC rCA rl r
∴r(可作为三角形内切圆半径公式)
根据上述阅读材料完成下列各题:
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、a3、…、an,合理猜想其内切圆半径公式(不需说明理由).
【参考答案】
1.B 2.C 3.D 4.D 5.D 6.B 7.C 8.C 9.C 10.B
11.2
12.
13.8.5
14.2
15.20
16.(1);(2)
17.(1)6;(2)1
18.BC=10cm,半径为cm.
19.(1)最小值为5;(2)这种汽车使用10年报废最合算,最少年平均费用为2.5万元;(3)r=2.
20.(1)cm;(2)40cm.
21.(1)17;(2)rA=3,rB=7,rC=14
22.(1)①2;②+2;(2)略;(3).
23.(1)边长分为5、12、13的三角形内切圆半径为2;(2)r;(3)内切圆半径r
同课章节目录
